MODEL MATEMATIKA SIR PADA PENYEBARAN PENYAKIT COVID-19 DENGAN EFEKTIVITAS VAKSIN
on
E-Jurnal Matematika Vol. 13(1), Januari 2024, pp. 38-44
DOI: https://doi.org/10.24843/MTK.2024.v13.i01.p439
ISSN: 2303-1751
MODEL MATEMATIKA SIR PADA PENYEBARAN PENYAKIT COVID-19 DENGAN EFEKTIVITAS VAKSIN
Ni Luh Gede Shindya Armita1§, Luh Putu Ida Harini2, Ida Ayu Putu Ari Utari3
1Program Studi Matematika, Fakultas MIPA-Universitas Udayana [armithashindya@gmail.com]
2Program Studi Matematika, Fakultas MIPA-Universitas Udayana [ballidah@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA-Universitas Udayana [idaayuputuariutari@unud.ac.id]
§Corresponding Author
ABSTRACT
Corona Virus Disease (COVID-19) is one of the disease outbreaks that has spread throughout the world since the end of 2019. This disease causes infected individuals to experience infections in the respiratory tract with a fairly high risk. One branch of mathematics that can help overcome this case is the formation of mathematical models. The model formed is the SIR model basically describes the spread of disease in the Susceptible (S), Infected (I), Recovered (R) classes, but in this study the Infected (I) class was classified into two and added parameters to decrease vaccine effectiveness. The former model is then used to find a solution in the form of a disease-free equilibrium point, where the point will be used to form a basic reproduction number. To prove that the equilibrium point found to be stable, a stability analysis will be carried out and in the model that has been formed it is found that the disease-free equilibrium point is locally asymptotic stable with the condition that. After analysis, it was found that the rate of decline in vaccine effectiveness was quite influential on the class of infection R0 < 1.
Keywords: Infection, Vaccination, COVID-19, SIR Model
-
1. PENDAHULUAN
COVID-19 merupakan varian jenis baru dari virus corona yang pertama kali ditemukan pada akhir tahun 2019 di Wuhan, China. Virus ini menyebabkan individu yang terjangkit penyakit mengalami infeksi saluran pernafasan dengan gejala awal yang ringan seperti penyakit influenza (Susilo, dkk ,2020). Walaupun kasus positif COVID-19 telah menurun akibat dilakukan berbagai upaya seperti, lockdown, karantina, vaksinasi dan lainnya, isu terkait COVID-19 ini masih menjadi topik hangat di kalangan masyarakat. Vaksinasi yang dilakukan oleh pemerintah sendiri belum optimal dan menjangkau keseluruhan masyarakat serta minat masyarakat untuk melakukan vaksinasi juga terbilang terus menerus menurun. Sejak awal vaksinasi dilakukan hingga tahun 2023, di Indonesia telah dilakukan vaksinasi hingga tahap dosis keempat, namun menurut data yang dikeluarkan oleh Kementerian Kesehatan Republik Indonesia melalui laman website https://vaksin.kemkes.go.id/#/vaccines per 30 Juni 2023 total masyarakat rentan dan umum yang telah mendapatkan vaksinasi dosis pertama adalah sebanyak 82,79%,
sedangkan untuk dosis kedua sebanyak 70,49%, dosis ketiga sebanyak 34,82% serta untuk dosis keempat hanya 0,84%.
Model SIR sendiri merupakan sebuah model epidemi yang paling sederhana dimana pada model ini akan dibentuk tiga buah persamaan diferensial yang bergantung pada waktu. Model ini dapat membuat kita memahami keadaan sistem pada saat ini dan membantu memprediksi keadaan di masa depan dengan menganggap total populasi konstan selama wabah penyakit ini terjadi.
Menurut Resmawan dan Yahya (2020) tingkat transmisi dari penyakit COVID-19 dapat ditekan dengan menekan tingkat interaksi antar individu terinfeksi dan individu rentan, serta dengan mengoptimalkan perawatan dan karantina bagi individu yang terinfeksi penyakit.
Menurut penelitian Fauzia (2021) setelah dilakukan simulasi data tindakan rawat inap pada pasien COVID-19, terlihat bahwa masih sangat banyak individu yang telah terinfeksi namun belum terdeteksi sehingga dapat memperpanjang rantai penyebaran virus COVID-19.
Pada penelitian Hartati(2021) model SIR dikembangkan menjadi SIQDR, yakni dengan menambahkan sub-populasi karantina dan meninggal akibat penyakit.
Mu`tamar et al. (2021) menyimpulkan bahwa faktor vaksinasi sangat berperan penting dan semakin tinggi efektivitas dari vaksin maka semakin efektif vaksin tersebut dalam menekan populasi terinfeksi. Berdasarkan pada penelitian-penelitian tersebut maka dilakukan penelitian selanjutnya, yakni mengembangkan model dasar SIR dengan membagi kompartemen individu terinfeksi menjadi terinfeksi sebelum melakukan vaksinasi dan individu terinfeksi setelah melakukan vaksinasi serta menambahkan laju penurunan efektivitas vaksin sebagai parameter.
-
2. METODE PENELITIAN
Penelitian yang dilakukan merupakan penelitian kualitatif dengan melakukan pengkajian referensi dari penelitian terdahulu serta buku-buku yang terkait dengan penelitian tersebut. Dalam proses penelitian, diperlukan metode-metode sebagai berikut guna mencapai tujuan penelitian yakni:
-
1. Melakukan pembentukan model matematika untuk penyebaran penyakit COVID-19.
-
2. Menentukan titik kesetimbangan pada model yang telah dibentuk.
-
3. Membentuk bilangan reproduksi dasar
-
4. Melakukan analisis kestabilan pada titik kesetimbangan.
-
5. Melakukan simulasi pada model yang telah dibentuk.
-
3. HASIL DAN PEMBAHASAN
-
3.1. Pembentukan Model Matematika
-
Pembentukan model matematika penyebaran penyakit COVID-19 diklasifikasikan menjadi empat kompartemen, yakni kompartemen Susceptible meliputi individu rentan (S), kompartemen Infected atau individu yang terinfeksi penyakit dibagi menjadi dua yakni terinfeksi setelah vaksinasi (I1) serta terinfeksi sebelum vaksinasi (I2), serta kompartemen individu yang sembuh dari penyakit (R'). Dalam pembentukan model akan digunakan beberapa asumsi, yakni:
-
1. Model yang dibentuk berlaku pada populasi tertutup atau tidak terdapat migrasi.
-
2. Terdapat kelahiran dan kematian alami dimana laju kematian sama dengan laju
kelahiran.
-
3. Jika laju kelahiran sama dengan laju kematian maka populasi akan konstan.
-
4. Seluruh individu yang lahir pada periode penyebaran penyakit diasumsikan rentan terhadap penyakit.
-
5. Model yang dibentuk berlaku pada populasi homogen.
-
6. Jumlah populasi tetap selama periode penyebaran penyakit dan valid dalam jangka waktu tertentu.
-
7. Individu yang telah sembuh tidak dapat kembali tertular ataupun rentan.
-
8. Tidak terjadi infeksi acak.
-
9. Masa inkubasi penyakit sangat singkat.
Berdasarkan pada asumsi-asumsi tersebut, maka akan dibentuk diagram transfer dari penyebaran penyakit COVID-19 dengan efektivitas vaksin. Sebagai berikut:
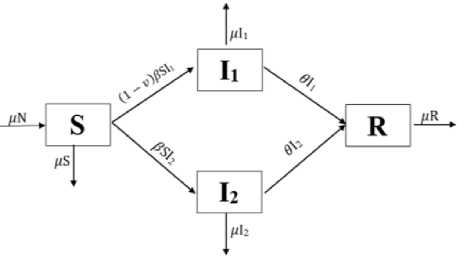
Gambar 1. Diagram Transfer Penyebaran COVID-19 dengan Efektivitas Vaksin
Diagram transfer pada Gambar 1. diperoleh dengan parameter sebagai berikut:
|
Parameter |
Definisi |
Syarat |
|
R β θ v |
Laju kelahiran dan kematian alami populasi individu Laju penularan individu rentan menjadi terinfeksi Laju kesembuhan tiap individu Laju penurunan efektivitas vaksin |
μ≥ 0 β≥0 θ≥0 v ≥ 0 |
Sumber: Data yang diolah sendiri
Berdasarkan pada diagram transfer pada Gambar 1. dapat bentuk model SI1I2R dalam sistem persamaan diferensial sebagai berikut:
dS z ,
— = μN-(1- v)βSh - βSI2 — μS at
dI1
-
- = = (1 - v)βSIι -Iι(μ + 0) dt
dl2
-
- = = βSI2-I2(μ + θ)
dR z .
-
— =θ(I1+I2)-μR
dt
I2 = 0 atau βS-μ-θ = 0 (7)
(1)
Dengan diketahui N = S +I1+12+ R dan
— = 0 dt
Selanjutnya untuk menemukan titik ekuilinrium bebas penyakit maka akan disubstitusikan I1 = 0 dan I2 = 0 ke persamaan (2) sehingga diperoleh
S = N
(8)
3.2. Eksistensi Titik Ekuilibrium
Titik ekuilibrium menggambarkan jumlah populasi yang manusia yang diharapkan pada kehidupan nyata. Berdasarkan pada definisi dari titik ekuilibrium akan dibentuk titik ekuilibrium dari sistem persamaan (1) sertakan dibahas eksistensi dari titik ekuilibrium pada persamaan (1) sebagai berikut.
Teorema 3.1. Diberikan R0 = jβ-, sehingga diperoleh:
1.
2.
3.
Jika R0 ≤ 1, maka sistem persamaan (1) memiliki titik ekuilibrium bebas penyakit Eo(N, 0,0,0)
Jika R0 > 1, maka sistem persamaan (1) memiliki titik ekuilibrium endemik
E ( μ+θ μ(Nβv-Nβ+μ+Θ)(R0-1) ΘIΛ
1 ∖^(1-v), (βN-μ-Θ')β(v-1') , , μ )
untuk I1 ≠ 0
Jika R0 > 1, maka sistem persamaan (1) memiliki titik ekuilibrium endemik E2 (-+θ, 0,^,θ∆mtukh≠^ β μ / 2
BUKTI
Untuk membuktikan teorema 3.1 maka sistem persamaan (1) akan dibuat dalam ke dalam
Karena I1 = 0 dan I2 = 0 atau tidak terdapat populasi yang terinfeksi, maka untuk populasi yang sembuh dari penyakit juga tidak ada sehingga R = 0, maka akan diperoleh titik ekilibrium bebas penyakit dari sistem persamaan (1), yakni E0(S = N ,I1 = 0,I2 = 0,R = 0) dimana kondisi ini merupakan kondisi disease-free
Selanjutnya akan dicari titik ekuilibrium penyakit dari sistem persamaan (1), berdasarkan persamaan (2) akan diperoleh
S = —^^^ 11(βv — β)— β⅛ — μ
Dari persamaan (3) diperoleh
(1-v)βSI1=L(μ + θ')
Jika I1 ≠ 0, maka
_ μ +θ = β(1-v)
Dari persamaan (4) akan diperoleh
I2 = 0 atau βS-μ-θ = 0
(9)
(10)
(11)
(12)
bentuk konstan sebagai berikut:
μN-(1- v)βSI1 - βSI2 -μS = 0(2)
Dari persamaan (3) akan diperoleh
I1 = 0 atau (1 — v)βS — μ — θ = 0(6)
Dari persamaan (4) akan diperoleh
Selanjutnya akan disubstitusi persamaan (11) ke persamaan (9) sehingga diperoleh
11 =
μNβv-μNβ+I2βμ+I2βΘ+μ2+μΘ β(μv+θv-μ-θ)
(13)
Jika I2 = 0 maka persamaan (5) dan persamaan
(13) akan menjadi
μ(Nβv — Nβ + μ + θ)
1 β(μv + θv — μ — θ)
θI1 R= —
μ
(15)
βN
Dengan diketahui R0 = -^, maka persamaan
(14) akan menjadi:
tersebut tidak bergantung terhadap waktu.
j _ μ(N βv-N β+.+O')(Ro-1')
1 (βn-μ-θ)β(v-1)
(16)
Sehingga akan diperoleh titik ekuilibrium untuk
E1(s = -0,R=θ^) μ /
μ+θ .
β (v-1)’ 1
μ(N β v-N β +μ+θ)(Ro-1) (βn-μ-θ)β(v-1)
>^2 =
dimana terdapat jumlah populasi
tertentu pada kompartemen sub-populasi yang terinfeksi sebelum melakukan vaksinasi dimana
nilai tersebut tidak bergantung terhadap waktu.
Selanjutnya akan dicari titik endemik dengan kondisi dimana I2 ≠ 0, sehingga persamaan (4) akan diperoleh
Jika I2 ≠ 0, maka akan diperoleh
Selanjutnya akan disubstitusikan persamaan (18) ke persamaan (9) sehingga diperoleh
12
I1βμv+I1βθv+Nβμ-I1βμ-I1βθ-μ2-μθ β(.+θ}
(19)
Jika I1 = 0, maka akan diperoleh
= μ(Nβ-μ-θ}
2 β(μ + θ)
(20)
βN
Dengan diketahui R0 = ^qp maka persamaan
(20) akan menjadi:
μ(Ro — 1) β
(21)
Selanjutnya akan disubstitusikan kondisi dimana I1 = 0 ke persamaan (5) sehingga diperoleh
θI2
R = — μ
(22)
Sehingga akan diperoleh titik ekuilibrium untuk c ( Q μ + θ j j .(R0-1) D θl2∖
E2(S = — l1 = 0>l2 = ~r~ 'r=~) dimana terdapat jumlah populasi tertentu pada kompartemen sub-populasi yang terinfeksi sebelum melakukan vaksinasi dimana nilai
3.3. Bilangan Reproduksi Dasar
Bilangan reproduksi dasar merupakan ukuran yang digunakan untuk menggambarkan potensi dari penyebaran suatu penyakit. Bilangan reproduksi dasar dari sistem
persamaan (1) dibentuk dengan menggunakan matriks generasi selanjutnya atau Next Generation Matrix (NGM). NGM dibentuk dengan menggunakan persamaan-persamaan yang menggambarkan infeksi penyakit yakni I1
dan I2, kemudian persamaan tersebut dibuat
kedalam matriks Jacobian berikut;
Γ (1-v)βS-μ-θ 0
j \ 0 Sβ-μ-θ
Selanjutnya akan disubstitusikan
(23) titik
ekuilibrium bebas penyakit ke dalam matriks Jacobian sebagai berikut:
(1-v)βN-μ-θ 0 1
7(Eo)"[ 0 Nβ-μ-θJ (24)
Selanjutnya lakukan dekomposisi pada matriks Jacobian menjadi matriks F dan V dimana F merupakan matriks transmisi dan V merupakan matriks transisi dan hitung R0 = p(FV-1) dimana (FV-1) merupakan matriks yang disebut dengan matriks generasi
selanjutnya dan R0 merupakan radius spectral atau nilai eigen terbesar dari matriks generasi selanjutnya.
FV- =
r (v-vβN 0 1
I
(v-1)βN
(25)
Dari persamaan (4) akan diperoleh nilai eigen dan nilai eigen terbesar yang akan menjadi bilangan reproduksi dasar, maka diperoleh:
R- Nβ
R0 = μ+θ
(26)
3.4. Analisis Kestabilan Titik Ekuilibrium
Bebas Penyakit
Analisis kestabilan dilakukan untuk mengetahui apakah solusi yang diperoleh bersifat stabil atau tidak. Pada penelitian sistem persamaan yang dibentuk merupakan sistem persamaan non-linear, maka dari itu akan dilakukan analisis kestabilan dengan menentukan nilai eigen dari matriks Jacobian yang akan diperoleh dengan melakukan linearisasi pada sistem persamaan (1) di sekitar titik ekuilibrium bebas penyakit.
J =
-
■ -(1-v)βI1-I2β -μ —(1 — v)βS —βS + μ
(1 — v)βl1 —(1 — v)βS — μ — θ 0
l2β 0 Sβ-μ-θ
-
- 0 θ θ
0
0
∩
0J (27)
— 1
Teorema 3.5. Jika R0 < 1 maka titik ekuilibrium bebas penyakit dari sistem persamaan (1) dinyatakan stabil asimtotik lokal.
Untuk membuktikan teorema tersebut maka akan dibentuk persamaan karakteristik dari matriks Jacobian dengan menggunakan persamaan det∖Jac — λl∖ = 0 dan diperoleh persamaan karakteristik sebagai berikut:
P(X) = (μ + λ)2(-(1 — v)βN + μ + θ + λ)(-Nβ + λ + μ + θ) (28)
Persamaan karakteristik tersebut kemudian akan dimuat ke dalam tabel Routh berikut:
|
λ4 λ3 λ2 λ1 λ0 |
b4 b3 „ _ b3b3-bibι r1 = b3 „ _ rlb1-b3b0 C1 = r, bo |
b2 b1 bo 0 0 |
bo 0 0 0 0 |
Sumber: Alam & Abadi (2021)
Pada Tabel 2. yang dihasilkan terlihat bahwa seluruh elemen kolom pertama pada tabel bernilai positif sehingga semua akar polinom akan bernilai negatif. Oleh karena itu, titik ekuilibrium bebas penyakit dari persamaan (1) stabil asimtotik lokal dengan syarat R0 < 1.
-
3.5. Analisis Kestabilan Titik Ekuilibrium
Endemik
Selanjutnya akan dicari kestabilan dari titik ekuilibrium endemik, dimana dari tiga titik yang diperoleh dua diantaranya merupakan titik ekuilibrium endemik yakni E1 dan E2. Analisis kestabilan dari titik ekuilibrium endemik akan diperoleh dengan cara yang sama dengan kestabilan titik ekuilibrium bebas penyakit, sehingga akan dibentuk matriks Jacobian dengan melakukan linearisasi pada sistem persamaan (1) di sekitar titik ekuilibrium endemik serta akan diperoleh persamaan karakteristik sebagai berikut:
1
P(X) = — -—-—— ((λv + μv + θ v —
v (v-1)(p+θ) μ
λ)(μ + λ)(Nβλμv + Nβμ2v +
Nβμθv — Nβλμ — Nβμ2 — Nβμθ — λ2μ — λ2θ + j3 + 2μ2θ + μθ2y)
P(λ) = X∑E((μv + θv + λ}(μ +
μ+θ
(29)
(30)
λ) (Nβλμ + Nβμ2 + Nβθ + λ2μ + λ2θ — μ3 — 2μ2θ — μθ2))
Dimana persamaan (29) merupakan persamaan karakteristik untuk E1 dan persamaan (30)
merupakan persamaan karakteristik untuk E2. Kemudian dari persamaan tersebut akan dibentuk tabel Routh seperti yang terlihat pada Tabel 2. Setelah dibentuk ke dalam tabel Routh diperoleh bahwa pada kedua titik ekuilibrium endemik tidak stabil, karena pada kedua tabel yang dibentuk diperoleh koefisien bernilai negatif pada kolom pertama tabel Routh.
-
3.6. Simulasi Model
Setelah dilakukan pembentukan model, selanjutnya akan dilakukan simulasi dari model matematika yang telah dibentuk dengan penggunaan program Matlab dengan tujuan untuk memberikan gambaran geometris yang terkait dengan model yang telah dihasilkan dan memberikan nilai untuk masing-masing parameter. Parameter dan total populasi akan diambil dari penelitian-penelitian terdahulu yang terkait dengan virus COVID-19 dengan tujuan sebagai bahan acuan utama dalam melakukan simulasi terhadap model yang telah dibentuk sebelumnya agar dapat memberikan gambaran secara geometris terkait dengan wabah penyakit tersebut. Parameter-parameter yang diambil dari penelitian sebelumnya diantaranya laju kelahiran dan kematian alami (j'), laju penularan individu rentan menjadi terinfeksi (β), laju kesembuhan tiap individu (θ) yang diambil dari penelitian Hartati (2021), serta Laju penurunan efektivitas vaksin (v) yang diambil dari penelitian Alam dan Abadi (2021). Adapun nilai–nilai dari parameter yang akan digunakan disajikan dalam tabel berikut:
Tabel 3. Nilai-nilai Parameter
|
Parameter |
Nilai |
Satuan |
|
μ β θ v N |
0,00625 0,0001 0, 07142857143 0,002667 100 |
perhari Individu |
|
hari Individu | ||
|
hari Satuan populasi |
Sumber: Alam & Abadi (2021), Hartati (2021) dengan perubahan
Nilai-nilai parameter pada Tabel 3. selanjutnya akan disubstitusikan ke sistem persamaan (1) dan
akan dicari bilangan reproduksi dasar dengan menggunakan metode New Generation Matrix dengan asumsi sebagai berikut:
-
1. Jika R0 < 1 maka penyakit diperkirakan akan menghilang
-
2. Jika R0 > 1 maka penyakit diperkirakan akan menyebar atau semakin mewabah
-
3. Jika R0 = 1 maka penyakit diperkirakan akan menetap
Setelah dilakukan substitusi nilai parameter, diperoleh bilangan reproduksi dasar dengan nilai R0 = 0,1287. Karena nilai R0 < 1 maka penyakit COVID-19 yang di muat dalam model sistem persamaan (1) diasumsikan tidak akan semakin menyebar atau akan segera menghilang dari populasi dalam jangka waktu tertentu.
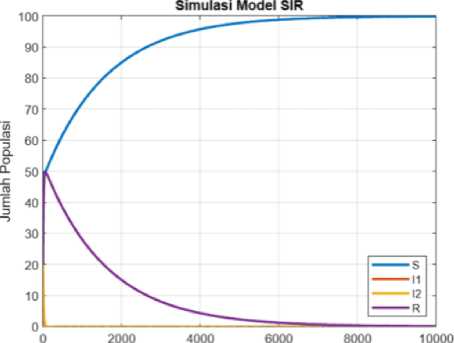
Selanjutnya akan dilakukan simulasi numerik pada titik ekuilibrium bebas penyakit E0 = (S = 100, I1 = 0, I2 = 0,R = 0) dengan menggunakan bantuan software Matlab berdasarkan nilai parameter pada tabel 3 dan sebarang nilai awal S(0) = 50 ,I1(0) = 8 ,I2(0) = 22 ,R(0) = 20 disajikan gambar sebagai berikut:
Waktu
Gambar 2. Plot Sistem untuk R0 < 1
Berdasarkan Gambar 2. dapat terlihat perubahan jumlah populasi dimana untuk populasi infeksi I1 dan I2 akan secara signifikan menuju nol dan stabil di titik tersebut serta karena tingkat penularan penyakit yang rendah, maka tingkat kesembuhan dari penyakit (R) juga akan stabil di titik nol karena tidak terdapat infeksi, serta untuk populasi rentas (S) akan mengalami peningkatan dikarenakan tingkat infeksi yang rendah. Berdasarkan hasil simulasi yang telah dibentuk dapat dikatakan jika parameter yang terbentuk pada sistem memenuhi syarat R0 < 1 maka penyakit akan dapat dikendalikan dan perlahan akan menghilang dari populasi dalam jangka waktu tertentu.
Selanjutnya akan dilakukan simulasi pada titik
ekuilibrium endemik E2 = (S = 776,7857143, I1 = 0, I2 = -54,45402299, R =
-622,3316913 ), untuk R0 > 1. Untuk membuat kondisi dimana R0 > 1 maka nilai parameter β akan diperbesar menjadi 0,003 dan untuk parameter 0 diperkecil menjadi 0,01 serta parameter v diperkecil menjadi 0,0002667,sehingga bilangan reproduksi dasar dari sistem persamaan (1) adalah R0 = 18,4615. Karena R0 > 1 maka penyakit COVID-19 yang dimodelkan ke sistem persamaan (1) diasumsikan akan menyebar atau akan terjadi pandemi. Berikut adalah hasil simulasi dengan menggunakan nilai parameter β yang telah diperbesar, dengan sebarang nilai awal S(0) = 50, I1(0) = 20 ,I2(0) = 35,R(0) = 30.

Waktu
Gambar 3. Plot Sistem untuk R0 > 1
Berdasarkan pada Gambar 3. terlihat perubahan pada jumlah populasi, dimana populasi rentan (S) menurun karena tingkat penyebaran atau tingkat infeksi dari individu yang belum melakukan vaksinasi meningkat serta untuk populasi individu yang sembuh dari penyakit terlihat menurun dikarenakan tingkat kesembuhan dari penyakit yang rendah. Berdasarkan hasil simulasi yang telah dibentuk dapat dikatakan jika parameter yang terbentuk pada sistem memenuhi syarat R0 > 1 maka akan terus terjadi epidemi atau penyakit akan terus menerus menyebar.
-
4. KESIMPULAN DAN SARAN
-
4.1 Kesimpulan
-
Berdasarkan hasil yang diperoleh setelah melakukan pengembangan model epidemi pada penyakit COVID-19 diperoleh bahwa, parameter yang berpengaruh secara signifikan terhadap penyebaran penyakit COVID-19 adalah laju penularan penyakit serta laju kesembuhan tiap individu. Laju penularan
penyakit sendiri dapat dipengaruhi dengan melakukan vaksinasi sehingga dapat memperkecil ruang penyebaran penyakit.
-
4.2 Saran
Adapun saran yang diberikan untuk pemerintah yakni dapat melakukan kegiatan edukasi kepada masyarakat hingga minat masyarakat untuk melakukan vaksinasi lebih tinggi serta kesadaran masyarakat akan pentingnya melakukan vaksinasi untuk penanggulangan penyakit akan lebih meningkat.
DAFTAR PUSTAKA
Alam, M. F., & Abadi. (2021). Model
Matematika Penularan Penyakit Covid-19 Dengan Penerapan Vaksinasi Dua Dosis: Studi Kasus Di Sidoarjo, Indonesia. MATHUNESA Jurnal Ilmiah Matematika, 09(03), 501–513.
Fauzia, L. A. (2021). ANALISIS PEMODELAN MATEMATIKA
PENULARAN COVID-19 DENGAN TINDAKAN RAWAT INAP di RUMAH SAKIT. MATHunesa: Jurnal Ilmiah
Matematika, 9(1), 126–132.
https://doi.org/10.26740/mathunesa.v9n1.p1 26-132
Hartati, Eti, P. S., Matematika, F., & Sains dan Teknologi, Universitas Islam Negeri Syarif Hidayah, J. (2021). MATH unesa. In MATHunesa: Jurnal Ilmiah Matematika (Vol. 9, Issue 2).
https://doi.org/10.26740/mathunesa.v9n1.p1 26-132
Mu`tamar, K., Putra, S., & Perdana, S. A.
-
(2021) . Analisis Penyebaran Covid-19 Dengan Menggunakan Model Sir Dan Vaksinasi Serta Estimasi Parameter. BAREKENG: Jurnal Ilmu Matematika Dan Terapan, 15(2), 323–334.
https://doi.org/10.30598/barekengvol15iss2 pp323-334
Resmawan, R., & Yahya, L. (2020). Sensitivity Analysis of Mathematical Model of Coronavirus Disease (COVID-19)
Transmission. CAUCHY: Jurnal Matematika Murni Dan Aplikasi, 6(2), 91–99.
https://doi.org/10.18860/ca.v6i2.9165
Susilo. Adityo, Rumende. C.M, Pitoyo. C.W, Santoso. W.D, Yulianti.M, Herikurniawan, Sinto.R, Singh. G., Nainggolan.L., Nelwan. E. J.,Chen. L. K., Widhani. A., Wijaya. E., Wicaksana. B., Maksum. M, Annisa. F., Yunihastuti. E. (2020). Coronavirus Disease 2019 : Tinjauan Literatur Terkini, Jurnal
Penyakit Dalam Indonesia, 7(1), pp. 45–67.
44
Discussion and feedback