PENGELOMPOKAN SAHAM MENGGUNAKAN K-MEANS DALAM PEMBENTUKAN PORTOFOLIO OPTIMAL
on
E-Jurnal Matematika Vol. 12(4), November 2023, pp. 302-308
DOI: https://doi.org/10.24843/MTK.2023.v12.i04.p433
ISSN: 2303-1751
PENGELOMPOKAN SAHAM MENGGUNAKAN K-MEANS DALAM PEMBENTUKAN PORTOFOLIO OPTIMAL
Ade Ayu Nita Devi1§, Komang Dharmawan2, Ni Ketut Tari Tastrawati3
1Program Studi Matematika, FMIPA-Universitas Udayana [Email: adeayunitad@gmail.com] 2Program Studi Matematika, FMIPA-Universitas Udayana [Email: k.dharmawan@unud.ac.id] 3Program Studi Matematika, FMIPA-Universitas Udayana [Email: tastrawati@unud.ac.id] §Corresponding Author
ABSTRACT
K-Means clustering analysis is a technique used in grouping objects that have similar characteristics. In forming a portfolio, investors need a group of stocks from different sectors that aim to build a well-diversified portfolio. Portfolio diversification is the placement of assets from various stocks in such a way that risks can be minimized. This study aims to obtain the results of grouping stocks with K-Means at IDX80 and then determine the optimal portfolio of each cluster formed using the Mean Variance method in the period January, 1st 2020 to November, 10th 2022. As a result, obtained in this study that grouping with K -Means produces four groups and P4 is the best portfolio consisting of 10 stocks with a Sharp ratio performance value of 0.0062 with a risk portfolio of 1.59% and an expected return portfolio of 0.17%.
Keywords: Portfolio, Mean Variance, K-Means, Sharp Ratio
dalam menyusun portofolio mean variance akan melakukan diversifikasi dengan menentukan kombinasi pemilihan sejumlah aset sehingga risiko dapat diminimalkan.
Diversifikasi portofolio bisa dilakukan hanya memfokuskan pada saham saja. Akan tetapi, akan timbul pertanyaan seperti saham apa saja yang layak dijadikan portofolio. Tidak semua perusahaan layak untuk diinvestasikan maka dari itu investor harus terus mempertimbangkan dengan baik pengalokasian asetnya. Alokasi aset diibaratkan seperti meletakkan telur (dalam hal ini adalah uang atau modal investor) pada keranjang yang tepat. Dengan cara ini investor akan terlindungi dari kerugian yang signifikan dan meningkatkan peluang untuk mendapatkan return yang lebih baik atas investasi nya.
Demi memperoleh manfaat dari diversifikasi, tentunya investor harus tahu tentang karakteristik saham yang akan dijadikan portofolio. Karakteristik aset yang dimaksud meliputi tingkat return harapan serta klasifikasi industri suatu aset. Kombinasi saham yang dipilih oleh investor memengaruhi kinerja portofolio investasi. Untuk mendapatkan
kelompok saham dengan karakteristik yang sama maka akan digunakan algoritma pengelompokan yaitu analisis klaster. Analisis klaster merupakan teknik yang digunakan untuk mengelompokkan kumpulan objek yang memiliki karakteristik serupa. Saham yang menunjukkan karakteristik yang sama masuk ke dalam satu kelompok dan seterusnya sampai setiap saham ditempatkan ke dalam satu kategori. Dengan kata lain, analisis klaster dapat memberikan investor manfaat diversifikasi yang paling optimal.
Analisis klaster digunakan sebagai langkah awal yang tepat dalam memilih sekuritas-sekuritas untuk dijadikan portofolio. Salah satu metode klasterisasi yang paling sering digunakan adalah K-Means (Sani, 2018) K-Means clustering adalah salah satu algoritma unsupervised learning yang digunakan untuk mengelompokkan data berdasarkan kesamaan variabel. Cara kerja algoritma ini cukup sederhana yaitu dimulai dengan menentukan jumlah klaster kemudian membaginya dengan banyak data berdasarkan kedekatan objek dengan titik pusat cluster atau centroid. Selain tergolong dalam metode yang sederhana, K-Means juga sangat cepat dan efisien dalam melakukan pengelompokan data (Muningsih, 2018).
Beberapa penelitian telah dilakukan sehubungan dengan penerapan analisis klaster untuk menyeleksi saham dalam pembentukan portofolio optimal. Siregar et al. (2021) melakukan klasifikasi harga saham harian indeks LQ45 periode Januari 2015 sampai September 2021 dengan menggunakan metode K-Means kemudian menentukan portofolio optimal dengan model Markowitz. Analisis klaster K-Means menunjukkan hasil yang baik dalam mengategorikan saham sehingga diperoleh portofolio optimal dengan performa yang baik juga. Ridwan et al. (2021) melakukan penelitian yang berfokus pada teknik klasterisasi saham IDX30 berdasarkan nilai expected return dan Value at Risk.
Putra et al. (2021) melakukan seleksi portofolio dari indeks Kompas-100 berdasarkan kesamaan kurva pergerakan harga kemudian membandingkan bobot portofolio Mean Variance dan Equal-Weight. Penelitian tersebut memperoleh hasil bahwa pengelompokan saham berdasarkan kesamaan kurva pergerakan harga sangat menjanjikan dalam pemilihan portofolio dan Mean Variance tampil lebih unggul dengan nilai Sharpe Ratio yang tinggi dan dengan
volatilitas yang rendah. Investor dalam berinvestasi memiliki banyak pilihan indeks yang bisa digunakan sebagai acuan perdagangan. Seperti pada IDX80 yang terdiri dari 80 saham yang memiliki kinerja harga yang baik sehingga dapat menjadi alternatif acuan bagi investor dalam melakukan investasi.
Berdasarkan uraian pada paragraf sebelumnya penelitian ini bertujuan untuk mengetahui hasil pengelompokan saham IDX80 dengan menggunakan K-Means kemudian menghitung portofolio optimal pada masing-masing klaster kemudian mengukur kinerja dari portofolio yang terbentuk.
Standarisasi data dilakukan jika terdapat perbedaan ukuran seperti nilai skala yang besar pada variabel yang akan diteliti. Standarisasi Z-score merupakan cara yang umum digunakan dalam mengonversi setiap variabel terhadap nilai standar yang dapat dihitung menggunakan persamaan (1)
z = xi-x ((1) s
dengan xi merupakan data ke-i, X merupakan rata-rata data, dan s merupakan simpangan baku.
K-Means clustering merupakan metode non-hierarchical clustering yang bertujuan untuk mengelompokkan data menjadi suatu bentuk atau lebih klaster yang bekerja secara berulang-ulang untuk mendapatkan kelompok data yang optimal. Pusat awal klaster dipilih
secara acak kemudian akan dihitung jarak setiap data dengan pusat awal klaster dengan
menggunakan jarak Euclid seperti pada persamaan (2)
((2)
Jn
∑ (Pk-Qk)2
Data yang memperoleh jarak terpendek akan membentuk sebuah klaster dan centroid
baru dihitung dengan mencari rata-rata data dari setiap klaster seperti pada persamaan (3)
n
v = - V Xi
n
1 = 1
((3)
dengan xi merupakan objek ke-i dan n merupakan jumlah objek yang menjadi anggota klaster.
Metode Elbow digunakan dalam menentukan klaster optimal dengan memberikan informasi berupa grafik yang menunjukkan nilai within
cluster sum square (WCSS) dan nilai k yang
mengalami penurunan (Syakur et al., 2018)
K
WCSS =∑∑(Xi - Ck)2
K=1XiESκ
((4)
dengan Xi merupakan data ke-i dan Ck merupakan centroid klaster ke-i.
Perhitungan portofolio optimal dimulai
dengan menghitung return dan expected return dari saham. Return merupakan imbalan yang dihasilkan dari investasi selama beberapa periode waktu (Tandelilin, 2017). Nilai return dengan asumsi tidak ada pembayaran dividen
tunai dapat dinyatakan dengan persamaan (1) (Francis & Kim, 2013)
. Pit
Ri,t = ∖nτ-÷^ i — 1,2.....n pi,(t-i)
((5)
dengan Ri,t adalah return pada saham ke-i periode ke-t, dan Pit adalah harga saham pada saham ke-i periode ke-t. Dengan asumsi probabilitas suatu keuntungan adalah sama, expected return dapat ditulis menggunakan persamaan (6)
1 v' ((6)
E(Ri) = τ∑Ti,t 'i
t=1
= 1,2, ...,n
Risiko dihitung dengan mencari nilai deviasi standar atau varians yang mengukur penyimpangan realized return dengan expected
return. Risiko dapat diukur dengan persamaan (7)
1 ((7)
σi = t -1 ∑(Ri't
t-1
-E(RO)2
Kovarians merupakan ukuran yang menunjukkan arah antara return dua aset.
Kovarians dua aset dapat dihitung dengan persamaan (8)
<>ij ((
_ ∑lι(Ri,t-E(Ri))(Rjιt-EV 8)
T — 1 dengan σij adalah kovarians antara saham i dan saham j.
Expected return portofolio dihitung dengan mencari rata-rata tertimbang dari setiap expected return masing-masing saham dalam portofolio. Expected return portofolio dapat diselesaikan dengan persamaan (5) (Francis & Kim, 2013)
n
E(Rp) = ∑ WiE(Ri)
((9)
i=i
dengan Wi adalah bobot saham ke-i dalam
portofolio. Jumlah bobot saham dalam
portofolio dinyatakan seperti persamaan (10)
n
∑wi =1 i=i
((10)
Risiko portofolio bukanlah rata-rata
tertimbang dari semua risiko pada saham tunggal karena setiap saham dapat mengalami kinerja pergerakan yang sama. Risiko dapat
bernilai lebih kecil dari rata-rata tertimbang setiap saham tunggal. Risiko portofolio dapat
dinyatakan dengan persamaan (7) (Hartono,
2010)
σP
dengan
n n
∑ ∑wiwjσij
i=i j=i
((11)
σp didefinisikan sebagai risiko
portofolio. Matriks varians-kovarians dibentuk berdasarkan persamaan (6) dan (8) kemudian dinyatakan dengan persamaan (12)
|
∑ |
r σ11 |
σ12 |
σ13 ••• |
σ1n ) |
((12 |
|
σ21 |
σ22 |
σ23 - |
σ2n | ||
|
— |
σ31 ⋮ |
σ32 |
σ33 - |
σ3n | |
|
Lσn1 |
σn2 |
σn3 - |
σnn- |
dengan ∑ didefinisikan sebagai matriks varians kovarians.
Bobot dari masing-masing saham pada portofolio optimal dengan nilai risiko minimum dapat dihitung menggunakan persamaan (13) (Francis, 2013)
_ ∑-11n ((13)
W lτ∑-il 1n∑ 1n
dengan ∑-1 adalah invers dari matriks varian kovarians dan 1n adalah vektor satu dengan ukuran n × 1.
Evaluasi kinerja dari portofolio sangat penting dilakukan. Salah satu ukuran dalam evaluasi kinerja portofolio adalah rasio Sharpe. Portofolio dengan rasio yang lebih besar dari portofolio lainnya dianggap baik karena menghasilkan nilai return yang lebih besar dari return investasi bebas risiko. Rasio Sharpe, dapat dihitung dengan menggunakan persamaan (14) (Francis et al., 2013)
ς _ rv-rf (14)
Sp p σp
dengan Tp merupakan expected return
portofolio Tf merupakan return bebas risiko, dan σp merupakan risiko portofolio selama periode pengamatan.
-
2. METODE PENELITIAN
Penelitian ini menggunakan data sekunder yang diperoleh dari https://finance.yahoo.com. Data tersebut merupakan data yang bersifat kuantitatif yaitu data harian harga penutupan (closing price) dan data volume harian saham pada IDX80 periode 1 Januari 2020 hingga 10 November 2022.
Berikut merupakan langkah-langkah yang dilakukan dalam menganalisis data dalam penelitian ini:
-
1. Mengumpulkan dan menyeleksi data historis saham yang tergabung dalam IDX80 selama periode 1 Januari 2020 sampai dengan 10 November 2022 kemudian menghitung variabel data yaitu expected return dengan menggunakan persamaan (6), varians dengan menggunakan persamaan (7), dan rata-rata volume penjualan.
-
2. Melakukan standarisasi pada variabel yang sudah dihitung sebelumnya menggunakan persamaan (1).
-
3. Pengelompokan Saham dengan K-Means
-
1. Menentukan jumlah klaster optimal digunakan metode Elbow pada persamaan (4).
-
2. Menentukan pusat awal klaster (centroid) secara acak.
-
3. Menghitung jarak objek terhadap centroid dengan menggunakan persamaan (2).
-
4. Mengelompokkan objek ke dalam centroid terdekat.
-
5. Menghitung centroid baru dengan
menghitung rata-rata data dengan
menggunakan persamaan (3). Ulangi
langkah ke-3 sampai langkah ke-5 jika
posisi centroid masih berpindah sampai centroid stabil.
-
4. Menentukan portofolio optimal model mean variance
-
a. Menghitung expected return dan varians saham masing-masing klaster
menggunakan persamaan (6) dan (7).
-
b. Menghitung kovarians menggunakan persamaan (8) kemudian membuat matriks varians-kovarians.
-
c. Menentukan bobot optimal masing-masing portofolio dengan menggunakan persamaan (13).
-
d. Menghitung expected return dan risiko portofolio masing-masing klaster dengan persamaan (9) dan (11).
-
5. Menghitung nilai rasio Sharpe dari masing-masing portofolio dengan menggunakan persamaan (14).
-
3. HASIL DAN PEMBAHASAN
Terdapat 75 saham yang konsisten tergabung dalam IDX80 pada periode penelitian. Setelah memperoleh saham konsisten, langkah selanjutnya adalah menghitung variabel pengelompokan K-Means yaitu expected return, varians, dan rata-rata volume penjualan. Karena variabel yang digunakan memiliki satuan nilai yang berbeda, maka dilakukan standarisasi data yang bertujuan untuk menyamakan satuan pada variabel.
Setelah memperoleh variabel yang sudah distandarisasi, selanjutnya dilakukan pengelompokan saham dengan K-Means yang diawali dengan menentukan jumlah klaster optimal dengan menggunakan metode Elbow. Penentuan jumlah klaster optimal berdasarkan metode Elbow dapat dilihat pada Gambar berikut
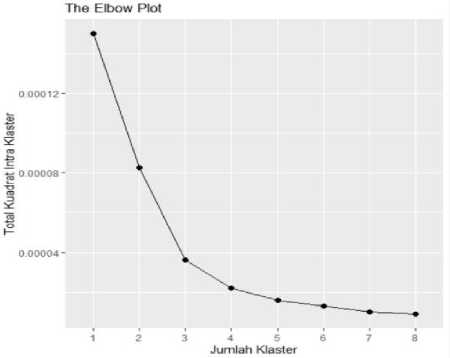
Gambar 1. Jumlah Klaster Optimal
dapat dilihat terdapat penurunan garis yang terjadi pada rentangan jumlah k=3 menuju k=4 yang menandakan bahwa kurva mulai melandai pada empat klaster. Dengan demikian dipilih 4 klaster sebagai jumlah klaster yang optimal.
Pengelompokan saham dengan K-Means dimulai dengan menentukan 4 centorid secara acak. Kemudian masing-masing objek dikelompokkan berdasarkan jarak terdekat dengan centorid. Selanjutnya dihitung centorid baru dan diulangi sampai centroid tidak berpindah atau stabil. Hasil pengelompokan dengan menggunakan K-Means dapat dilihat pada Gambar 2.
Cluster plot
Dιm2 (19 4%)
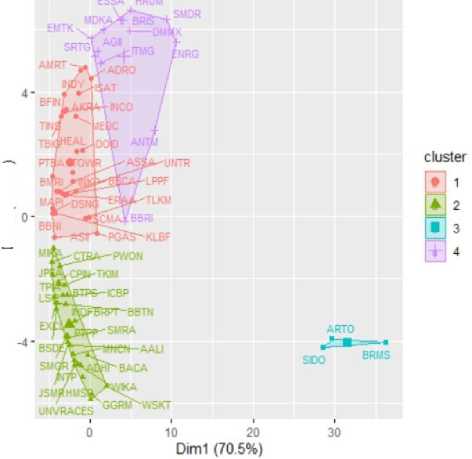
Gambar 2. Hasil Pengelompokan Saham Dengan K-Means
Berdasarkan Gambar 2 dapat dilihat bahwa pengelompokan saham dengan K-Means menghasilkan 4 klaster yang optimal dengan masing-masing anggota klaster dapat dilihat pada tabel berikut.
Tabel 1. Saham Anggota Pada Setiap Klaster
|
Klaster |
Jumlah Anggota |
Saham Anggota Klaster |
|
P1 |
29 |
ADRO, AKRA, AMRT, ASII, ASSA, BBCA, BBNI, BFIN, BMRI, DOID, DSNG, ERAA, HEAL, INCO, INDY, INKP, ISAT, KLBF, LPPF, MAPI, MEDC, PGAS, PTBA, SCMA, TBIG, TINS, TLKM, TOWR, UNTR |
|
P2 |
30 |
AALI, ACES, ADHI, BACA, BBTN, BRPT, BSDE, BTPS, CPIN, CTRA, EXCL, GGRM, HMSP, ICBP, INDF, INTP, JPFA, JSMR, LSIP, MIKA, MNCN, PTPP, PWON, SMGR, SMRA, TKIM, TPIA, UNVR, WIKA, WSKT |
|
P3 |
3 |
ARTO, BRMS, SIDO |
|
P4 |
13 |
AGII, ANTM, BBRI, BRIS, DMMX, EMTK, ENRG, ESSA, HRUM, ITMG, MDKA, SMDR, SRTG, |
Langkah berikutnya membentuk portofolio optimal dari keempat klaster yang terbentuk kemudian akan dipilih portofolio dengan kinerja terbaik yang memiliki nilai rasio sharpe tertinggi. Sebelum itu, dihitung terlebih dahulu expected return, varians, dan matriks varians-kovarians secara berturut-turut menggunakan persamaan (6), (7), dan (8). Sebagai contoh expected return dari klaster P3 disajikan dalam tabel berikut:
Tabel 2. Expected Return setiap saham pada Klaster
P3
|
No |
Saham |
Expected return |
|
1. |
ARTO |
0.0006 |
|
2. |
BRMS |
0.0019 |
|
3. |
SIDO |
0.0002 |
Selanjutnya, dihitung nilai kovarians antar saham pada masing-masing klaster dengan menggunakan persamaan (8). Sebagai contoh nilai kovarians pada klaster P3 dalam bentuk matrikas varians-kovarians sebagai berikut:
0.0062 0.00005 0.0006
∑=∣0.00005 0.0015 -0.0003
0.0006 -0.0003 0.0610
Setelah memperoleh expected return dan matriks varians-kovarians pada masing-masing klaster P1, P2, P3, dan P4. Dengan bantuan software MATHLAB ditentukan portofolio-portofolio efisien dari setiap klaster P1, P2, P3, dan P4 yang disajikan pada Gambar berikut.
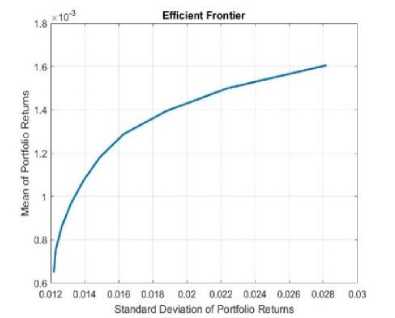
Gambar 3. Portofolio Efisien Klaster P1
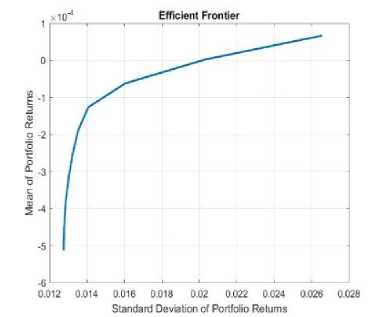
Gambar 4. Portofolio Efisien Klaster P2
Tabel 3. Nilai Bobot Optimal pada Klaster P3
|
No |
Saham |
Bobot |
|
1. |
ARTO |
19% |
|
2. |
BRMS |
79% |
|
3. |
SIDO |
2% |
Kemudian, dari data bobot masing-masing saham dalam masing-masing klaster dihitung nilai return portofolio menggunakan persamaan (9) dan risiko portofolio menggunakan persamaan (11) sehingga diperoleh hasil seperti pada Tabel 3 berikut.
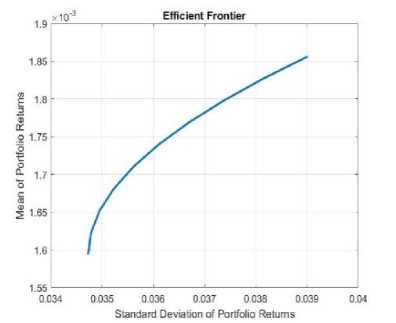
Gambar 5. Portofolio Efisien Klaster P3
Tabel 3. Nilai Expected Return dan Risiko Portofolio
|
Expected return portofolio |
Risiko portofolio | |
|
Pi |
0.06% |
1.22% |
|
P? |
-0.05% |
1.27% |
|
P3 |
0.16% |
3.47% |
|
P4 |
0.2% |
1.59% |
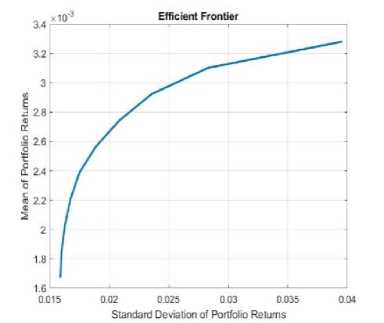
Gambar 6. Portofolio Efisien Klaster P4
Nilai expected return dan risiko portofolio yang sudah diperoleh dari masing-masing portofolio digunakan untuk menghitung rasio Sharpe yakni melakukan evaluasi terhadap expected return portofolio yang menghasilkan return lebih besar dari benchmark. Nilai benchmark menggunakan rata-rata harian suku bunga Bank Indonesia selama periode penelitian berlangsung sebesar 0,19% atau 0,0019 (www.bi.go.id). Rasio Sharpe dihitung menggunakan persamaan (14) secara lengkap disajikan pada tabel berikut:
Tabel 4. Nilai Rasio Sharpe setiap Klaster
|
Rasio Sharpe | |
|
Pi |
-0.103 |
|
P2 |
-0.109 |
|
P3 |
-0.0086 |
|
P4 |
0.0062 |
Berdasarkan Gambar 3 sampai dengan Gambar 6 dengan asumsi investor seorang risk averter, portofolio optimal dipilih dari portofolio efisien dengan nilai risiko paling minimum. Pembobotan dengan nilai risiko portofolio minimum dihitung menggunakan persamaan (13) kemudian sebagai contoh diperoleh kombinasi bobot dari klaster P3 yang disajikan pada tabel 3.
Berdasarkan Tabel 4 dapat dilihat bahwa nilai rasio Sharpe dari klaster P4 paling besar dibandingkan nilai rasio Sharpe dari klaster lainnya. Dengan demikian menunjukkan bahwa klaster P4 merupakan portofolio yang kinerja paling baik apabila dibandingkan dengan klaster yang lain berdasarkan perhitungan rasio Sharpe.
-
4. KESIMPULAN DAN SARAN
Pengelompokan saham menggunakan K-Means menghasilkan 4 klaster saham yang optimal. Jumlah klaster optimal ditentukan dengan menggunakan metode Elbow yang menunjukkan pembagian dari 75 saham yang terbagi menjadi 4 klaster yaitu P1, P2, P3, dan P4.
Dari 4 klaster yang terbentuk, dipilih klaster P4 yang memiliki nilai rasio sharpe terbesar. Pembentukan portofolio optimal pada klaster P4 menghasilkan kombinasi bobot yang optimal sebagai berikut: saham AGII sebesar 5% , BBRI sebesar 23%, DMMX sebesar 7%, saham EMTK sebesar 10%, saham ENRG sebesar 8%, saham HRUM sebesar 4%, saham ITMG sebesar 10%, saham MDKA sebesar 11%, saham SMDR sebesar 8%, dan saham SRTG sebesar 13%, dengan nilai expected return portofolionya sebesar 0.2% dan nilai risiko portofolio sebesar 1.59% pada satu hari investasi.
Bagi peneliti yang tertarik pada pengelompokan saham dengan menggunakan analisis klaster, banyak metode clustering lain yang belum digunakan seperti K-Medoid, Fuzzy C-Means, dan lain-lain. Selain itu, pada saat membentuk portofolio agar lebih
memperhatikan aspek lain seperti korelasi antarsaham agar investasi yang dilakukan dapat terlindungi dari kerugian yang besar.
DAFTAR PUSTAKA
Francis, J. C. (2013). Modern Portfolio Theory. John Wiley & Sons, Inc.
Hartono, J. (2010). Teori Portofolio dan Analisis Investasi (7th ed.). BPFE-Yogyakarta.
Muningsih, E. (2018). Komparasi Metode Clustering K-Means dan K-Medoids Dengan Model Fuzzy RFM untuk Pengelompokan Pelanggan. Evolusi, 6,
106–113.
Putra, Y. E., Saepudin, D., & Aditsania, A. (2021). Portfolio Selection of KOMPAS-100 Stocks Index Using B-Spline Based Clustering. Procedia Computer Science, 179, 375–382.
https://doi.org/10.1016/j.procs.2021.01.01 9
Sani, A. (2018). Penerapan Metode K-Means Clustering Pada Perrusahaan. 1–7.
Siregar, B., & Pangruruk, F. A. (2021). Portfolio Optimization Based on Clustering of Indonesia Stock Exchange: A Case Study of Index LQ45. Indonesian Journal of Business Analytics (IJBA), 1(1), 59–70. https://journal.yp3a.org/index.php/ijba
Syakur, M. A., Khotimah, B. K., Rochman, E. M. S., & Satoto, B. D. (2018). Integration K-Means Clustering Method and Elbow Method for Identification of the Best Customer Profile Cluster. IOP Conference Series: Materials Science and
Engineering, 336(1).
https://doi.org/10.1088/1757-899X/336/1/012017
Tandelilin, E. (2017). Pasar Modal Manajemen Portofolio & Investasi (G. Sudibyo, Ed.). PT Kanisius.
Yunita, I. (2018). Markowitz Model dalam Pembentukan Portofolio Optimal (Studi Kasus pada Jakarta Islamic Index). Manajemen Indonesia, 18(1), 77–85.
44
Discussion and feedback