SOLUTIONS OF NONLINEAR BOUNDARY SYSTEM WITH COUPLED INTEGRAL BOUNDARY CONDITIONS

E-Jurnal Matematika Vol. 12(4), November 2023, pp. 248-259

DOI: https://doi.org/10.24843/MTK.2023.v12.i04.p426

ISSN: 2303-1751

SOLUTIONS OF NONLINEAR BOUNDARY SYSTEM WITH COUPLED INTEGRAL BOUNDARY CONDITIONS

Raad Noori.Butris^1§, Hewa Salman Faris²

¹Dept. of mathematics, College of basic education, Duhok University, Iraq [Email: raad.butris@uod.ac] ²Dept. of mathematics, College of basic education, Duhok University, Iraq [Email: hewa faris@uod.ac] ^§Corresponding Author

ABSTRACT

This article presented some theorems on a novel non-linear multiple Integro-differential equations of boundary T-system. It has been studied the numerical-analytic method and Banach fixed point theorem for the existence and approximation of the solutions over considered boundary system in compact space. In this work, we demonstrate that the mention methods can be discussed and analyzed for the existence and uniqueness, of a solution for the vector system. The paper satisfies the Hölder condition.

Keywords: Nonlinear boundary system; couple integral boundary condition; existence and uniqueness solution; numerical-analytic method.

1. INTRODUCTION

Nonlinear boundary value problems play a crucial role in the study and management of real-world nonlinear systems and the advancement of innovations. These problems arise in several branches of science, engineering, and physics as wave equation in the physical differential equation that the determination of normal modes is often stated as boundary value problems. The theory of boundary value problems together with a set of additional limitations on the boundaries has a very wide collection of various methods. Conventionally, these methods can be divided into several main categories, namely analytic methods, functional analytical methods, numerical methods, and numerical-analytic methods (Samoilenko, 1985; Ronto, 2000).

The method proposed of boundary value that corresponds to the problem of a solutions of ordinary differential equation systems of first order with non-linear sides (Samoilenko, 1985). It should be remembered that the numerical-analytical approach is primarily aimed at investigating the qualitative problems of a solution's.

The numerical-analytic method is fairly universal and can be used for both the study of the problem of life and practical solution building. For the given differential equation, a boundary value problem involves finding a solution for the given nonlinear differential equations subject to multi -boundary conditions, which is a prescription for certain combinations of needed solution values and their derivatives at more than one point.

Recently, many types of Integro and Integral differential equations have been used to approximate the periodic solution of various different differential equations such as Volterra, Fredholm, and mixed Volterra Fredholm (Butris, 2020; Zavizion, 2009: Zill 2013). The method of successive approximation (numerical analytic method) is due to the simplicity and possibilities clear to approximate construction of a solutions of integro-differential equations. This study become more general and detailed than those introduced by (Butris, Faris, 2020).

The several lemmas and theorems from the numerical-analytical method, which has been used to study the solutions of the nonlinear boundary T-system (Butris, Faris 2020).

In this paper, the nonlinear Boundary system considered as follows:

dx dt

dy dt

— (λ₁ + B₁(^t))^χ + (^2 + B2(t))^y +f(t,x(t),y(t),u(t)

^{— (C}1 ⁺ ^1(^t))^{x + (}^2 + D₂(t)')^y

+g(t,x(t),y(t),v(t))

with Boundary conditions

-(1)

τ τ

∫ ∫ x(t)dtdt — d₁ + u(T)

0 0 τ τ

∫ ∫ y(t)dtdt — d₂ + v(T)

00

where, 0 < τ ≤ t ≤ T, d₁, and d₂ are constants, x ∈ D₀,y ∈ D₁, u ∈ D_u, andv ∈ D_v. The domains, D₀ and D₁ are closed and bounded subset of Rⁿ. Also D_v and D_u are bounded domains subset of R^m.

Consider the vector functions f(t,x,y,u) and g (t, x, y, v) on the following domains are defined and continuous:

(t, x, y, u) ∈ Rⁿ × D₀ × D₁ × D_u

— (— ∞ ,∞) × R²ⁿ × R^m   I

(t, x, y, v) ∈ Rⁿ × D₀ × D₁ × D_v∣

— (— ∞ ,∞) × R²ⁿ × R^m  J

-(2)

where, D0: ∣∣x - x0∣∣ ≤ r_x, D₁. ∣∣y - y0∣∣ ≤ r_y, D_u: ∣∣u∣∣ ≤ d_u and D_v: ∣v∣ ≤ d_v. And are continuous vector functions in x, y, u ,v.

The boundary system (1) verifies the continuous vector functions x(t,x₀,y₀) and y(t,x0,y0)                         where

Z1⁽t) — B₁(t)x(t,x₀,^y₀) + (A2 +

B2(t))y(t,x0,y₀} +

f(t, x(t, x₀,^y₀), y(t, x0,y0) u(t))        and

Z2⁽t) — (C1+D1(t))x(t,x0,y0) +

D2(t)y(t, x0,y0} +

g(t,x(t,x0,y0'),y(t,x0,^y0'),v(t')} which are defined as follows:

x⁽t, x0,y0)

— x₀e^A1t

t

+ ∫ e^A1(t-s (z₁(s)

0

- f∆(t, x⁽t, x0,y0~),y(t, x0,^y0), u(t))

+ ζ¹(t,x₀,^y₀j)ds,-(3)

as x(0,x₀,y₀) — x₀ and m — 0,1, -, where

f∆(t,x(t,x₀,^y0),^y(t,x₀,^y0),u(t)) — A1x0 +

;^^Ah7J₀^TeA1(T_s)z1^(s)ds,

A ²

^ζ (^{t, x}0^{, y}0) ^— T^^aI^t-TA₁-I) ^(d1 -

∫0 ∫0 ^F(t, x⁽t, x0, y0),y(t, x0, y0), u(t)) dt dt +

u(T)-^x°^τ(^e^^iτ-1^),-(5)

A1

det(A₁) ≠ 0, det(e^A1^T — TA₁ — I) ≠ 0 and

F(t,x⁽t),y⁽t),u⁽t)') — ^e^V^- (z1⁽s) — f∆(t, x(t, x0,y0),y(t, x0, y0), u(t))) ds.

-(6)

y(t,x0,y0) — y0e^c2t + ∫0^te^c2(^t-s) (z2(s) — g∆(t, x⁽t, x₀,^y₀), y⁽t, x0, y0) v⁽t)) +

ζ²(t,x0,y0))ds,-(7)

as y(0, x₀, y₀) — y₀ and m — 0,1, -, where

g^(t,x(t),y(t),v(t)) — C2y0 +

e^_-1∫^τ₀ ^ec2^(T-s}z2^(s^^-

^ζ2 (^{t, x}0^{, y}0)   τ(e^c2^τ-τc₂-ι) ^(d2

∫ ∫0 G(t, x⁽t, x0,y0~),y(t,x0,y0), v(t)) dt dt +

v-∏ ——).-.(9)

^c2

det(C₂) ≠ 0, det(e^c2^τ — TC₂ — I) ≠ 0, and

G(t,x(t∖y(t∖v(t)) — ∫0e^c2"^-s (z2(s^) —

g∆(t, x⁽t, x₀,^y₀),y⁽t, x₀,^y₀), v⁽t))) ds.

-(10)

Also we have

u(t) = f-∞f^Kι(t,s)^ι(t,s,x(s),y(s),p(s))dtds v(t) = ∫a f-∞^κ2(t,s)^2(t,s,x(s),y(s),ω(s))dsdt,

M and D2 = (D2ij) are non-negative matrices for i,j = 1,2, .,n and ∖∣. ∖∣ = max 1.1.

t∈[0,T]

We define the non-empty sets as follows:

»(11)

p(s) = fh^}(x(τ - y(^τ)) dτ ω(s) = f^s)(x(τ - y(τ)) dτ

Assume that the following inequalities are satisfied by the vector functions, f (t,x,y,u), g(t,x,y,v), ψ1(t,s,x,y,p) and ^2(t,s,x,y, ω):

∖f(t,x,y,u)∖ ≤B1,∖g(t,x,y,v)∖ <^₂,

^d/ = ^do ^{- r}x = ^do ^{- (}Q1^(t) (^d1 ^{- x}o^{τ2 +}

⅛k(e^-γι^α - e^-γι^b)e^γyτ) + ς1(t)R1tH^t1(t)),

.(20)

^Dg = ^D1 ^{- r}y = ^D1 ^{- (}&2^{(t) (d}2 ^{- y}0^T2 ⁺ ^^(b-a)) + ς2(t)R2tH^t2(t)), .(21)

...(13)

∖φ₁(t,s,x,y,p)∖ ≤ ξ1, ∖φ₂(t,s,x,y,p)∖ ≤

ξ2,                                 »(14)

∖f(t,xι,yι,Uι) - f(t,x₂,y₂,u₂)∖ ≤ Γj∖xι -x2∖^a + Γ2∖y1-y2 ∖∖V+ Γ3∖∖u1-U2∖V,

.(15)

∖∖g(t,x1,y1,V1) - g(t,x2,y2,V2)∖ ≤ ∑1∖x1 -x2∖^a + ∑2∖y1-y2∖^β + ∑3∖v1-V2∖^y,

.(16)

∖^1(t,s,x1,y1,p1)-^1(t,s,x2,y2,p2)∖ ≤ h1 ∖x1 - x2 ∖∖^a + h2 ∖y1 - y2 l∖^ + h3 ∖p1 -

p2∣r,                              .(17)

∖^2(t,s,x1,y1,ω1) - Ψ2(t,s,x2,y2,ω2)∖∖ ≤

11 ∣∖x1 - x2 ∖^a + I2 I∖y1 - y2 l∖^ + l3 ∖ω -

ω2∖∖^γ,                                »(18)

for all x,x1,x2 ∈D0,y,y1,y2 ED1,u,U1,U2 ∈ D_u and V,V1,V2 ∈ D_v, where ^1,^2, Γ1,Γ2,Γ3, Σ₁,Σ₂,Σ₃, h₁,h₂,h₃ and l₁,l₂,l₃ are positive constants, t ∈ [0,T], and 0 < a,β,γ < 1.

||e^i^(t-^s)^ ≤ R₁, ∣∣e^c2(^t-^s)∣∣ ≤ R₂, .(22)

H1(t) = ∖∖h2(t)-h1(t)∖∖,H2(t) = ∖h₄(t) -h3(t) ∖,                             .(23)

H*1(t) = ∣∖B1(t)∣∖∣∖x(t) ∣∖ + ∣∖A2 +

B2(t)∣∖∣∖y(t)∣∖+¾,                 .(24)

H*2(t) = l∖C1 + D1(t)∣∖∣∖x(t) ∣∖ + l∖D2(t)∣∖∣∖y(t)∣∖+¾. .(25)

Consider the sequences {x_m(t, x₀,y₀)}m=₀ and {y_m(t,x₀,y₀)}m=₀ of a continuous vector functions are defined as:

xm+1(t,xo,yo) = xoe^A1t +

f0^eA₁(t^-_s) (_ziιm(s)-

^f∆,m(^s, ^xm^(s, ^x0,^y0), ^ym^(s, ^xθ,^yθ'),^um^{(s)) +}

ζm¹(t,xo,yo))ds,                  .(26)

with x(0,x₀,y₀) = x₀ and m = 0,1, ., where

^f∆,m(^s, ^xm^(s), ^ym^(s),^um^{(s))   A}1^x0 ⁺

^at— ^τ^ e^A1(T-s)z_{1 m}(s) ds,       . (27)

ρAιT_-ι 0             ¹,^{m       ,}

From the boundary system (1), the positive matrices K₁(t,s) and K₂(t,s) are isolated singular kernels i. e.

∖K1(t,^)∖≤δ1e^-'^^

∖∖K2(t,s)∖≤δ2e-κ(^t-^s')

^ζ m(^t,x0^,y0)   _T(e^AiT_-TA1-i)^(d1

∫0 ∫^{τ F(}s, xm⁽s, xo, yo), ym⁽s, xo, yo), um(s)) dt dt +

umW-XTfe^-I)),         .(28)

where δ₁, δ₂, γ₁ and γ₂ are positive constants. Also A1 = (A_llj) A2 = (A2_ij), B1 = (B_uj), ^B2 = (^B2ij), ^B1 = (C1lj'), ^B2 = (C₂Ij), ^D1 =

F(t,xm(t),ym(t),um(t)) = f^e^-s) (z1m(s)-

^f∆,m ^(t, ^Xm^(t, ^χo, ^yo), ^ym ^(t, ^0' Yo)' U_m (t))) ds, .(29)

Um(t_lXo,yo~) =

£_m ∫_a ^K1⁽t, s)Ψ1(t, s,X_m(s),y_m(s),Pm(S) dt ds ,                                                       ...(30)

Pm⁽s) = !^(Xmtj) - Ym(τ)) dτ. . ⁽31)

Also we obtain that

ym+ι(t,χo,yo) = yoe^c2^t +

J_o^t_eC₂(t-s) ⁽_Z2,m^{(s) -}9∆,m(^t, ^Xm^(t), ^ym^(t), ^Vm^{(t)) +} ζm²(t,Xo,yo~))ds,.(32)

with y(0, X_o,y_o) = y_o and m = 0,1, ., where

∂∆,m(^t, ^Xm^(t), ^ym^(t), ^m^(t))   ^2^yo +

e⅛_-]∫o ^-^m^

C₂²

^ζ m^(t,Xo,yo) = _T(e^c2^T-_TC2-l) (^d2

∫∫^t ∫ G(t, Xm⁽t, X₀,^yo), ym⁽t), Vm(t)) dtdt +

Vm(T) - ^-(e^-I)),.(34)

G(t,Xm⁽t),ym⁽t),Vm⁽t)) = ∫^t_oe^c2^t-^s) (z2,m(s) -9∆.m(t,Xm(t,Xo,yo∖^ym(t,Xo,yo∖Vm(t)})ds ,                                   .(35)

Vm(t,Xo,yo) =

∫_a ∫l_mK2(t,s)ψ2(t,s,Xm(s),^y_m(s),ωm(s)} ds ,                                   .(36)

ωm(s) = ∫^(Xm(τ) - ym(τ)) dτ. . ⁽37)

Consider the matrix, φ_γ(T)'s highest Eigenvalue does not exceed one where, φ_γ(Γ) = (φι(^τ) φ2(^τ)∖ _{h ι} [φ₃(T) φ₄(T)) that is max                       .

√(φ1(τ}+φ4(τ}y²-4(φ1(τ)φ^             < 1

2                                         ^,

.(38)

where,

^φ1(^t) = R1^t ( ^Bi^(t)^ ^{+ γ}i ^{+ (r}3 ⁺

g1∞

R1tς1(t).

;)((h1 + _h3(H1(_t))')(.^,(e^-r^ιa-

e^-γ1^b)e^γ1^τ)) ),

.(39-i)

φ2(^t) = R1^{t (}^^2 ⁺ ^2(^t)∣ ^{+ γ}2 ^{+ (r}3 ⁺

R^((h2 + ^^^^	-Yia -
e-Y1b)eγ1τj) ),              .(39	— ii)
φ3(t^) = ^2t (HC1 + D1(t)∣ + ς1 + ^ς ⅛l^^	3.
.(39 -	iii)
φ4(t) = ^2t(∣θ2(t)∣ + ς2 + (∑3 + ⅛l^^     ).

.(39-iv)

₍.) _ e∣^¹∣T-HΛ1J∣τe^¹∣H∣^

>^1(t)        e∣∣^Λ1∣∣^T-τ∣μ₁∣H∣z∣∣

e^2∣^τ-∣C2∣τe∣^^

e\^|C²\^|T-τ∣∣C2∣|-||I||    ^,

■ ,ς2(t) =

₍ ) = _-HΛ_i∏(e∣^^ι∣∣Mz∏)_-^¹^ '   τ(eH^ι∏^τ-τ∏^₁∏-∏Z∏),

l∣C2ll(e∣∣^c2∣∣^t-∣∣∕∣l)

τ(e∣∣C²∣∣^τ-τ∣∣C2∣H∣z∣∣),

.(40)

P2⁽t) =

.(41)

^e∣^ι⅛∣           e"^c2"^t-∣∣I∖∣

^μ1(^t       ∣Aι∣   ^,μ2(^t       ∣∣C2∣∣   . ⁽⁴²⁾

Definition 1. A function f: S → ^ satisfies a Holder condition of order a where, 0 < a < 1, on [a, b] ∈ K, if there is a constant K > 0, so that V X,y∈[a,b], ∖f(X) - f(y)∖ ≤ K∖x-y∖^a.

Lemma 1. Suppose that x_i ∈ K and q ∈ (0,∞), then we received that

If x_i ≥ 0 and q ≥ 1, then for 1 ≤ i ≤ m, ∑^≤ (∑T=ιXtY ≤m^∑LιX*.

The reverse holds if 0 < q ≤ 1. Hence for 1 ≤ i≤m, (∑⅛)^q≤∑E⅛^q.

If Xι,yι ∈ K and 0 < q ≤ 1, then for 1 ≤ i ≤

m, Hx₁ — yj^ ≤ ^x_i-y_i^.

Lemma 2. Consider f(t, x, y) be a continuous vector function on, [0,   T]. Then

∣∣fθ(f(s,x(s),y(s)) -¹f₀^τf(τ,x(τ),y(τ))dτ)ds^ ≤ a(t)M holds, where α(t) = 2t (1 — ^) and M = max ∣∣f(t,x(t),y(t))∣∣,∀ t ∈ [0,T].

^∈L⁰,^τ J

Lemma 3. The following inequalities hold under conditions (23), (37) and (39) also from Lemma (1):

IIPm(O — Pm-1(0H^y ≤ ∣∣x_m(t) — x_m-ι(t)∣^γ(Hι(t)}^γ + ∣y_m(t)-y_m-1(tW(H1(t))^γ,

∣∣ω_m(t)-ω_m-₁(t)∣r≤ ∣∣xm(t)-xm-ι(t)∣r(H₂(t))^y+ ∣∣ym(t)-ym-ι(t)IK(H₂(t))^y

Theoreml. Suppose that u(t), v(t), ψ₁(t,s,x,y,w) and ψ₂(t,s,x,y,v) be continuous vector functions in the domain (2) and satisfy the conditions and inequalities (17), (18), (30), (31), (36) and (37) and the relations of (39). Then the following inequalities hold:-

• i)    l∣‰(t) — Um-ι(t)∣ ≤ (hi + h₃(H1(t))^y)(^-(e^-y1“ — e^-y1b)e^y1^t) ∣∣xm(t) — xm-i(t)∣∣ + (h2 + h3(HιCt))^y)(^(_e^-^-e^e^llymW—ym-^^

ii)∣Vm(t) — Vm-1(t)l ≤ (^ + ⅞(H2(t))^y) P²^) ∣xm(t) — xm-1(t)ll +

(Z2+∕3(H2(t))^y)P²^)lIymω^ ym-1(t)l,

for all t ∈ [0, TJ and m = 1,2,3,....

Remark. For the the definitions and lemmas, see (Butris, Faris 2020).

• 2.    APPROXIMATION OF A SOLUTIONS OF BOUNDARY SYSTEM (1).

The following theorem proposed the approximation of the solution of the boundary system's (1):

Lemma 4. Suppose that the vector functions f(t, x, y, u) and g(t,x,y,v) are defined and continuous on [0, TJ . Therefore the equations (3) and (7) are a solutions of boundary system (1).

dx .

Proof. Rewrite the differential equation — in the form of d^ using the boundary system (1) and the assumption that x = ve^A1t as follows:

d^ = B₁(t)v + (^₂ + B₂(t))we^C2te^-A1t + e^-A1tf(t, x,y, u).

Take the integral on both sides and put in x = ve^A1t, where z₁(t) = (B₁(t)x(t, x₀,y₀) + (^2 +B2(t))y(t,xo,yo) + f(t, x⁽t, x0, y0), y⁽t, x0, y0), u⁽t)))

to obtain that

x(t,x0,y0) = x0e^A1t + f₀^fe^{A1(t s}¼(s) ds.

Next, we have to find the periodic of x(t, x₀,y₀) and put the periodic solution in boundary condition to have:

∆=   _a A¹2----_s (^x0^τ (e^A1^T — ∕) +

T(b^a1^t-TA₁-I) A₁ ^{v          j}

f^τ₀ f₀^τ f₀^t e^A1(t-s)Z1⁽s) ds dt dt — d1 — u(T)).

The solution of, dχ in (1) will be:

x(t,x0,y0) = x0e^A1t + f₀^fe^A1(t-s) (z^s) — f∆(t,x(t),y(t),u(t)) + ζ¹(t,x0,y0))ds.

By the same method where y = we ^c2^t and

Z2⁽t) = (Cι+ Dι(t))x(t,Xo,yo) +

D2(t)y(t, X0,y0) +

g(t,x(t,X0,y0),y(t,X0,y0),v(t)} we get the

equation (7) as:

for 0 ≤ t ≤T.

Proof. According to (3)-(6), (11)-(12) and (43) also by the inequalities (13), (40) and (41) with condition (24) we have:

y(t,Xo,yo) = yoe^c2^t + f0e^{c2t s)} (z2(s) — g∆(t,X(t),y(t),v(t)} + ζ²(t, Xo,yo))ds.

Lemma 5. Suppose that the vector functions f(t,X,y,u) and g(t,X,y,v) are defined and continuous on [0,T] . Then from the inequalities (40) and (41) we see that the vector

∖Eι(t,Xo,yo)∖ ≤

(e^HA1Ht-HiH)(HAiHdi-x₀T²HAiH) . T(e^HAiHT-T\\Ai\\-\\i\\)

Hf^e^liC^t-S) (z₁(s) —

—^C, ^e/h'^{r s})(^zι(s))ds

Ai²

T(B^aI^t-TA₁-I)

—

τ τ t

^(fo ∫0 ∫0 ^{eA1(t S) (z}1^(s)

—

(∖E1(t,X0,y0)∖∖ ≤ ∖∖E2(t,Xo,y_o)∖) ^-

) T² +^1^1(e~^ι^a-

Yi²

+ς1(t)R1tH*1(t)

—

e-^γ1fe)e^γ1^τ)∖

_eA₁τ_-1 ∫o e^{A1(T S)} (z₁ (s)) ds) ds dt dt —

∫-^τ∞ fa KIT, s)ψι(T, s, X⁽s),y(s),p(s)) dT ds)) ds||,

∖

$2 (^t) ^(d2 ^{— y}0^T2 + ~~2 ^{(b — a))} +ς2(t)R2tH*2(t)

∕

≤ ^/Mel^Al^^-Wid!—^ +

-   T(B^haiht-THAiH-HIH)

e^HA1HT-H/iHTe^HA1Ht-HiH       *

eHAιHT-τ∖AιH-HiH   R1^{tH 1(t) +}

^,

_-l∕⅛A⅛H‰≤ιfι (_e-γ_ia

T(e^HAiHT-T\\Ai\\-\\i\\) Yi²

_—

e^-γι^b)e^γι^τ,

holds, where the equations (3) and (7) have derived to get the following:

≤

E^^y,) = ^-*¹^^ 1∖   ⁰∣J0J        T(B^aI^t-TA₁-I)

dι-x₀T²+^(e-y^ιa-e~'

f₀^te^l1(^{t S)}(zi⁽s) — fafa e^l'^iτ-^(^z_i(s))^ds

T(e«^Ai«^T-T\Ai\-\i\) e^HA1HT-HAiHTe^HA1Ht-HiH       *

BH^aIH^t-THA₁H-HIH   R1^{tn 1(t).}

Thus we obtain that

_—

Ai²

T(B^aI^t-TA₁-I)

^τ (^τ _f^t_eAι(t-s) (_zr_s)~

Vo ^fo ^fo ^{e        (z}1^(s)

eAlT-]fo e^{A1(T s})(zι(s))ds)dsdtdt —

f-^τ∞ fθ, Ki ⁽T, s)ψι (T, s, X(s),y(s), p⁽s)) dT ds)) ds

∖Eι(t,Xo,yo)∖ ≤ Qι(t) (di — XoT² + ⅛⅛-(e^-γι^a — e^-γ1^b)e^γ1^τ) + ς₁(t)R₁tH∖(t).

Yi²

+

^,

-(43)

By repeating iterations (7)-(12) and also (24), (40), and (41) we obtain that

_{E (tX y)} = (^ec2t-1K^c2^d2^-y₀τ²c2) ₊ ²^ ^, 0^,y0)       τ(e^c2^τ-τc₂-ι)

f^t₀e^{c2t S)}(z2⁽s⁾ — _ec^c-fa^c2ct-s∖^z2^cs^

l∖E2⁽t,Xo,yo)∖≤ Q2⁽t) (d2 —yoT² + ^δ^(b — a)‰2(t)R₂tH*2(t).

^γ2

C2²

τ(e^c2^τ-τc₂-ι)

_—

(f_o^Tf_o^Tf0e^c2(t-^⁾(z2^) —

So from ∖∖Eι(t,Xo,yo)∖∖ and ^E2(t,×o,yo)^ we receive the vector form:

eCτ_-I∫o e^c2(^{t S)}(z2⁽s))ds)dsdtdt —

fa f-∞ ^κ2 ⁽T, s)Ψ2 (T, s, X(s),y(s), ω(s)) dsdT)) ds

^,

.„ (44)

∕∣∣E'ι(t,Xo,yo)∣∣∖ ≤ ∖∣E2(t,Xo,yo)∣/ ^-

∕ρ1(t) (d1-xoT² + -¼-'1^α - e^-^M1^τ)∖ +ςι(t)RιtH*ι(t)

domain (2) . Firstly, by lemma (5) and from

(26) where, z-,o(t) = B-⁽t)xo⁽t,xo,yo) + (^2 +^2(t))yo(t,xo,yo) +

f(t, xo ⁽t, xo, yo),yo ⁽t, xo, yo), Uo ⁽t)) we get:

Q2(f) (d2-yoT²+-f(b-α))

∖             +ς2(f)R2tH*2(f)

x-(t,xo,yo) = xoe^A1t +

∕

3. EXISTENCE OF A SOLUTIONS OF

BOUNDARY SYSTEM (1).

The following theorem proposed the existence of the solution of the boundary system's (1):

∫o e^{A1(t s)} (zι,o(s) - (Λi%o + ^∑rh7∫o^τe^¹(^τ-s) ^(z1,o^{(s)) ds}) ⁺ ((d _-

T(t^a1^t-TA₁-I)   ¹

£X U^teA1(t-S) (^z1,o^{(s) -} (Λ1^xo ⁺

Theorem2. Consider f (t,x,y,u) and g (t, x, y, v) be vector functions on the domain (2) which are defined, continuous and satisfy all inequalities (15)-(19), conditions (22)-(23) and (38)-(41). Then the function’s sequences (26) and (32) of converge uniformly as m→∞ to the limit functions x⁰(t, x_o,y_o) and y⁰ (t, x₀,y₀) are a solutions of boundary system (1):

^A^-yJ^¹^ ^{s) (z}1,o^{(s)) ds}))^ds) ^{dtdt + u}0^{(T) -} ⅛^^{a1t - 1}))) )^ds,

= xoe^A1t + ∫0 e^{A1(t s)} (z1,0(s) - A^ +

-^a1 ^t _eA1(T-s)                    ^a1!≤1____

e^A1^T-I^Jo ^e       (Zw(S)) as ⁺ t(_g^a1^t-ta₁-I)

_-

_____A12______ γ^t γ^t Γ^t_eA1(t-s) T(g^a1^t-TA₁-I) ^J0 ^J0 ^J0

(∣x⁰(t,xo,yo) -xo⁽t,xo,yo)∣) v          yo) -yo(t,xo,yo)∣'

S₁ ξ₁ d₁-x₀T²+ 1-^-(e^-v1^a -e^-/1²

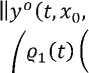
_____A12______ γ^t γ^t Γ^t_eA1(t-s)

T(g^a1^t-TA₁-I) ^J0 ^J0 ^J0

______A12______ (-^t (-^t Γ^t_eA1(t-s)

T(g^a1^t-TA₁-I) ^J0 ^J0 ^J0

(z₁,_o(s))dsdtdt +

(A₁x₀) ds dt dt -

≤

∖

+ς1(t)R1tH*1(t)

5₂(t)(d₂ -y₀T² + ^²⁽b

∖             /2

+ς2(t)R2tH*2(t)

^{- a))}

∕

^,

...(45)

(∣x⁰(t,xo,yo) -x_m(t,xo,yo)∣∖ ≤

Vl∣y⁰(t,xo,yo) -y_m(t,xo,yo)∣∣/ ^_ φ^(T)(l-φ_y(T))^-1Ωι(T),       .(46)

where,                             Ω₁(T) =

(ρ-(t) (d--xoT² + -¾e-^^a - e^-^M1^τ)∖

∖

+ς-(t)R-tH*-(t)

^2 ^{(t) (d}2 ^{- y}0^T2 ⁺ ~ ^{(b - a))}

+ς2(t)R2tH*2(t)

∕

and I is an identity matrix.

Proof:The function’s sequences

{x_m(t,xo,yo)}∞=ι and {y_m(t, xo,yo)}∞=- are

defined on (26) and (32), continuous on the

A1² T(g^a1^t-TA₁-I)

Uo(T)

_-

⅝A1(_e^a1^t-i)

TA^aT-I J0^T e^{A1(T s})(z₀(s)) ds ds dt dt +

(g^a1^t-TA1-I).

;^)ds,

= „ ₊^₁d₁^A≤^-zL ₊

• ^{0 +} T(s^a1^t-TA₁-I)

Xo(e^A1^-i>(e^A7-AT-i) _ ^

T(s^a1^t-TA₁-I)           (s^a1^t-TA₁-I)

j^e^a-s) (z1,o(s))ds-

^{A1(eA1t-l) t} f^τ f^t_eA1(t-s) (   (_sΛ_dsdtdt +

T(_eA1T_-TA1-I)Jo ^jo ^jo ^{e (}Z^{1,o(S)) ds dtdt +}

-A⅛A±Z)-(_{u  (T)})

T(t^a1^t-TA₁-I) V^{U1,0     ,}

= _ι ^A1⁽e^A1t-^l)(d1-Xo^T2) ,

• ^o      T(t^a1^t-TA₁-I)

j^e^tt-s) (_z1,o(s))ds

—i⅛⅛~^I∣^t I^t C e^A1^(t-s) (z₁₀(s)) ds dtdt +

T(T^a^^t-TA₁-I) o o o             ¹,⁰

,^r^-1) ‰<,(T)).

T(e^A1^T-TA₁-I)   ^-,0

Then by the mathematical induction and where, m = 0 we get the norm

Hx1(t,xo,yo) -xo∣ ≤

∣AaXΓ!A1!!-∣∣)(⅛-Ξo^

T(TH^aIH^t-TIA₁I-III)

((_e∣∣⁷ι∣∣'-τPι∣H∣∕∣∣)-Pι∣∣τ(e∣∣^           * _ω

⁽         (_eMι∣∣r-τ∣μι∣H∣∕∣∣)         ) KitHiW +

≤ R_it

J^⅛1⅛L ≤W (p -γ₁α

T(>Mi∣∣T-t∣M₁∣H∣∕∣∣) _n^{2 (e}

—

_e-Y₁b)_eγ₁T,

^(r3 ⁺

W^iI^r-P_iIrelkik-M ^i^71l7-TwHM

PilKe^ll^^1llt-Imi)

(∣Bi(t)∣ + Γi +

R_itτ(e∣∣⁷i∣∣'^r-p_i∣∣Te∣∣⁷ι∣∣^t-∣∣∕∣∣)

≤

PJk '¹> Wmnpi-⅛τ²+∣¹Uk ''>"-e ''I^jJd'¹'')

T(el^¹»^r-T|^i|-|/|) e∣71∣^r-ρ_i∣re∣71∣^^  f w* m

eP1∣∣'-τ∣μ₁∣H∣∕∣∣      ^{it   i(t).}

M^)/)^^

I) (^^{i +}

_—

+

e^-γι^δ)e^γι^τ)) ) IlXi(t) —Xoll +

Hx1(t,X0,y0) — Xoll ≤ 51(0 (di — XoT² + ⅛(e^-yι^α — e^-γι^d)e^γι^τ) + ς₁(t)R₁tH*₁(t).

Yi²

e∣7¹∣^r-PιPe∣7¹∣∣-ⁱ      _ePι∣∣T-τPi∣∣-∣∣∕∣∣

^γ2 ^{+ (r}3 ⁺

PiiKe^ll71llt-IM)

^ll(∣M2 + B2(t)H +

Using the same iterations as equation (32) also (24), (40) and (41) we get:

Hyι(t,%o,yo) — yoll ≤ ρ2W (d2 —yoT² + ^(6 —a)) + ς2(t)R2tH*2(t).

^γ2

RgTpkiH'-pJlTeikik-H/ll)

M^)/)^^

I) (⁽^^{2 +}

_—

e^-γW)e^γι^τ)) )|yi(t)—yol.

Thus from (39)-(41) we receive

For m ≥ 1 and by mathematical induction we have obtained that:

ⁱX2(t,Xo,yo) — Xi(t,Xo,yo)ⁱ ≤

Ritςi(t)(IBi(t)I + Γi + (Γ3 +

Hx_m(t,%o,yo) — %o! ≤ 5i⁽t) (di —XoT² + ⅛(e^-γι^α — e^-γ1^d)e^γ1^τ) + ς₁(t)R₁ tH*₁(t), Yi²

01(0 Riki(P)

1.^(fti + ^Hi^^^

_—

e^-γ₁s)e^γ>^τ)) )∣iX₁(t)-Xo∣i +

Hy_m(t, χo,yo) — yo^l ≤ 52⁽t) (d2 — yoT² + ^s-^(b — a)) + ς2(t)R2tH*2(t).

^γ2

^R1^t?1^{(t) (i}^2 ⁺ δ2(^t)^{i + γ}2 ^{+ (r}3 ⁺

giCW RikiOT

; )((_Λ2 + Λ3⁽Hi(t)^)Y)(cYi1₇⁽e-^γi«

_—

Beside that from (20), (21) and V t ∈ [0,T] where X₀ ∈ Dy and y₀ ∈ D_g we obtain that x_m(t,Xo,yo) ∈ D0 and y_m(t,Xo,yo) ∈ Di.

In addition, we have to demonstrate the sequences {Xm(t, X₀,y₀))m=₀ and {ym(t,X₀,y₀))m=₀ are uniformly convergent on (2). Then by lemma (5) and (26)-(31) when m = 1 we obtain that

e-^γι^)e^γι^τ)) )|yi(t)—yo∣.

By the same iterations from (32)-(37) and (39)-(41) we have

∏X2(t,Xo,yo) — Xi(t,Xo,yo)¹ ≤ ∣∣p —

-^^τ(-—(^t _eA₁d-s) Ig (s) + (Wi^r-Tzi_i-/) )∫o^e       L"^{1 (S)Xi (S) +}

⁽^2 ⁺ ¾C^s))^yiC^s) ⁺

f (s , Xi (s),^yi(s), Ui(S)) — (βi (S)Xo + (∕½ +

#2 (s))yo + f (t , Xo, yo, Uo))] ds

Λ₁(W^it-/) _r ,          ,

_f . _τ-----W- [u₁ (T) — U_n(T)]

T(e⁷i^τ-T A₁-I)^{l n y 0}^

+

Ny2(t,Xo,yo) — yi(t,Xo,yo)ⁱ ≤ β2tς2(t)(Ici + Di(t)I + Σi + (Σ3 + R2⅛)(('i ^{+ ,}3¾^γXPp))^γ^ Xo∣∣ + ^R2t?2⁽t) (!^(Oll + ∑2 + (∑3 + R^)((<2÷⅛¾^γ)(pp)y)ll^ yo∣^l∙

Since for, m> 1 and by induction, we demonstrate from (39) a vector form as follows:

∕∣^lχ_m+ι(0 -^χm(OH) ≤

VHym+ι(0 -ym(0H/ “

( (1(t) (2(0)0lXm⁽0-Xm-I(OII)

⁽ φ3(t)   φ4(θΛl∣ym(O-ym-1(OIM^,

where two sides' maximal t values have been ordered by iterated recurrence on (39)

(∣km+1CO -XmCOH) VHym+ι(^)-ym(^)H7

(i(T)   φ₂(T)∖^m

≤( φ3(T)   (4(T))

(e"^γι^α

—

_e-r1⅛)_er1τ)∖

∖

+ςι(T)RιTH∖(T)

Q₂ ^{(T) (d}2 ^{- y}o^τ2 ⁺ “~ ^{(b -} <0)

+ς₂(T)R₂TH*₂(T)

∕

■■■(47)

From (47) and for any k ≥0 we conclude that

_-

(^Hxm+k^(T'^{) X}m^(T)H)_<. (Hym_+k(T)-ym(T)H∕-

(H^Xm+k^(T) × ^Hym+k^(T)

^Xm+k-1^(T)H) ^ym+k-1^(T)H'

_-

+ ∙∙∙ +

_-

(∣Xm+1(T) -Xm(T)I) VHym+ι(T)-ym(T)H7^,

Rewrite the vector structure as follows:

^m+k(T)<(!-φ_γ(T)-∖m(T}Ωι^

,               - (∣Xm+k(T) - Xm(T)IA

where, ⅛₁+,ω - Mk(T) -y_m(T)∣∣(

⁽pi^(T)   (2^(T))

^φγ(T)-^ φ₃(T)   φ₄(T))  and ^^1(T^^-

∕ρι(t) (di -X0T² + ^(e"^γ1^α - _e^-γι⅛)_e^γ1r)∖ +ςι(0RιtH∖(0

MO (d2-y0T² + ^δ-^(b-a)}

∖              +ς₂(t)R₂tH*₂(t)              ∕

.

As a result of condition (38) we get

lim φm(t) — 0. Accordingly, n→∞ ^z

^{Xm⁽t, Xo, yo^)}m=o and ^{ym⁽t, Xo,yo^)}m=o

sequences of the function converge uniformly on the domains (20) and (21).

So the function’s sequences {X_m(t, X₀,y₀)}m=₀ and {y_m(t, X₀, y₀)}m=₀ converge uniformly on the domains (20) and (21).

Suppose that, lim X_m(t,X₀,y₀) —

m→∞

X (.t,X₀,y₀), and lim y_m(t,^χo,yo) — m→∞

y(t,Xo,yo).

• 4.    UNIQUENESS SOLUTION OF BOUNDARY SYSTEM (1).

The uniqueness solution of boundary system (1) is stated by the following theorem.

Theorem 3. With all conditions and hypotheses of previous theorem (4), the solution of boundary system (1), is a unique of (20) and (21).

Proof. Let r(t,X₀,y₀) and w(t,X₀,y₀) be another a solutions of (1), that is

r(t,Xo,y_o) — Xoe^A1t + ∫₀^te^¹(^t-s) (∑ι,_rCO -f∆,_r(t, r⁽t, Xo, yo), w⁽t, Xo, yo), MO) + ζ¹_r(t, X0,y0S)ds,

with r(O,Xo,y_o) — Xo, 2ι,r(s) — Bi⁽s)r⁽s) + (^2 +B2(s))w(s) +f(s,r(s),w(s),Ur(s)),

W⁽t,X₀,y₀) — yoe^c2^t + ∫0^t e^c2(^t-s) (z₂,r(s) -9∆,w(t, r⁽t, Xo, yo), w⁽t, Xo, yo), ^r(t)) + ζ²_w(t, Xo,yo))ds,

with w(0, Xo,yo) — yo, m — 0,1,2,....

We have

^HX⁽t,Xo,yo)-r⁽t,Xo,yo^)H ≤

e∣∣^H∣7-μ_i∣^e∣∣Λd^

R1^t   (_el∣Λι∣∣T-_r∣∣A₁∣∣-∣∣∕∣∣) (HMOU ^{+ r}1 ⁺

;)((^ftι⁺

HA⅛∣1¹⅛O

^(r3 ⁺

R^Tk^iH'r-HAjlTe^iUMl/ll).

^^iwrx^e^-»-.-

_-

e^-γι^)e^γι^)) )∣X(t)-r(t)H

e∣∣⁴1∣∣^r-∣∣^lι∣∣Te∣∣⁴1∣∣^t-∣∣∕I∣

■^R-———— (O- ■ o∙mι ⁺

^γ2 ^{+ (r}3 ⁺

IMιll(e∣∣⁴1∣∣^t-∣∣∕∣∣)

;)⁽⁽^ ⁺

R₁ET(Sll-⁴Ill^r-Ilzl₁IlTelI-⁴IlI^t-IIfIl)

M^t)/)^^

—

_e^-∕1⅛)_e∕1^τ)) )ly(t)—w(t)∣.

Ikfo^yo) —Kt,⅞,yo)H

≤ φ1 CO ∣∣X(t, Xo, yo) — r⁽t, Xo, yo) Il

+ ^2⁽^⁾!y⁽t^oJo⁾

— w(t,Xo,yo)∣∣∙                        ...(48)

To achieve the norm bellow, the same procedures are followed. Thus

lly⁽t, ^o,yo) —W(CJoJo)!

≤ ^3(r)lx(t,xo,yo) —^(t,^o,yo)H

+ ^4COHyk,⅞,yo)

— wk,%o,yo)H∙                   .(49)

We receive a vector form, from (48) and (49) as follows:

∕∣kk,⅞,yo) — Kt,%o,yo)H v IkCt^yo) —w(t,χo,yo)∣^l

(^ι(D ^2(O)(lkk,χo,yo)

V ^3⁽O   ^4⁽O/Vlkk,χo,yo)

_—

_—

r(C,Xo,yo)! ) wk,Xo,yo)∣^l/

Hence from condition (38), the greatest Eigen value of, φ_y(T)'s matrix is less than one, thus we deduce that, X(t) = r(t) and y(t) = w(t). This implies that the boundary system (1) has a unique solution.

• 5.    EXISTENCE OF THE FUNCTIONS Δ/ AND Δg OF BOUNDARY SYSTEM (1).

The existence solution of the boundary system (1) is uniquely linked with the existence of zeros of the functions ∆√t,Xo,yo) ∈ Oi × ¾1 → B and ∆₅(t,Xo,yo) ∈ O2 × ⅞2 → ^β defined by (4) and (8) respectively. Therefore the function sequences (26) and (27) are obtained from the approximate solutions (3) and (7).

Theorem 6. Assuming that all of theorem (4)'s assumptions and conditions are fulfilled, the following inequality holds:

(∣∆_f(t,Xo,yo) — ∆_f,m(t,Xo,yo)∣∖ ≤ C∣∣∆∕t,Xo,yo) — ∆_p,m(t,Xo,yo)∣/ ^-

μφm⁺¹(T) (/ —φ_y(T))^-1Ω1(T),

.(50)

where,

∩ι(T) =

_;0T²+l⅛(e-∣'1^ ₈

Γ1

+ς1(T)R1TH*1(T)

^^B

∖

£2 (^t) (⅛ ^{— y}o^T2 ⁺ ■“ (^ ^{— α}))

+ς2(T)R2TH*2(T)            ∕

HiiH

^, B = WfeX B1 = _e∣∣4₁∣∣T,∣∣_f∣∣ ^and B2 =

√⅛J1 ■ for all m≥ 0.

e∣∣^c2∣∣^τ-∣∣∕∣∣

Proof. From the equations (3) and (22) we have

∣∣∆∕t, Xo,yo) — ∆._Λm⁽t,Xo,yo⁾||

≤

^A1 e⁴1^τ-Z

f ^e41T-/^-TA1^{e41t   τ} A1(τ-S) f _f A _

( (e⁴1^τ-τA₁-z) )∫o ^{e        (Z1(i)}

Z1,mk))ds +

^τi1²     Γ^t_pA

(e⁴1^τ-τi₁-z) ∫o ^e

¹(^{t s}) (z₁(s)

IIi₁II²

_—

¾mk))d-S + ‰(T))∣∣

τ(e∣∣⁴1∣∣^r-τ∣μι∣H∣z∣∣)

||(u(T) —

r JA1∣I^(e∣4¹∣T-τ∣A1I^^

≤ [e∣∣⁴1∣∣^τ-∣m∣     (e∣∣⁴1∣∣^τ-τ∣∣A1∣∣-∣∣Z∣∣)

e∏_rST-⅛jj-u] ∣∣(¾ω^—⅛ω) ∣∣ +

-P₁ij_l^(≤¹-Tz.τ010-Z2ς∣0

.e∣∣⁴1∣∣^τ-∣∣z∣∣      (e∣∣⁴1∣∣^τ-τ∣H1∣∣-∣∣z∣∣)

[

^z1,m

_—

' ∣∣z₁HR₁t (e∣⁴ι"^r-τHz₁He'∣4¹"tΞ∣Z∣)

_—

_—

e∣∣⁴1∣∣^r-∣m∣     (e∣∣⁴1∣∣^r-T∣∣l1∣∣-∣∣Z∣∣)

^1,mCO ) ‰(T))∣∣

HZ1H²

τ(e∣∣⁴¹∣∣^r-τ∣μ1∣∣-∣∣z∣∣)

||(u(T) —

≤R1Tμ1(t)(IIB1(t)H + Γ1 + (Γ3 +

01(0 R1tς1(t)

;)((_Λ1+_Λ3(H1(t))^y)(c^^11₇(_e^-^¹«—

_e^-T1⅛)_e∕1^τ)) ^(t) — Xo∣∣ + ^R1^TB1^{(t) (}l^2 ⁺ ^2^(t)l ^{+ γ}2 ^{+ (r}3 ⁺

01(0 RiOiCO

■ )((⅛_i+⅛≡(Sι(_t))^,)(⅛(_t-'¹∙-

_e^-^)_ey₁τ)) )∣∣y₁(t)-yo∣∣

min a₁+e₁≤x≤b₁-e₁ c1+e2≤y≤d1-e2

max a₁+e₁≤x≤b₁-e₁ d+e2≤y≤d1-e2

^∆g,m^(t,^χ0,^y0⁾ ≤  ^1m

^∆g,m^(t, ^xo, ^yo) ≥ ^1m

∣∣∆∕t,%o,yo) - ∆_z,_m(t,χo,yo)y ≤ μι^ι(t)lk(O - x_m(t)∣∣ + μ1<P2(OI∣yW -y_m(t)ll                              ^(51)

.(54)

We get the same results under the same inequality and constraints and by doing the same steps

∣∣∆∕t,%o,yo) - ∆₅,_m(t,χo,yo)∣∣ ≤ μ2Φ1(t)l∣x(O - XmCOII + μ2^2(t)∣^lyW -y_m(t)∣.                            -(52)

Rewrite (51) and (52) in a vector form as:

So the boundary system (1) has a solutions, x _ x(t, x_o,y_o) andy _ y(t, x_o,y_o) suchthat

xo ∈ [α1 + ρAO (d1 - x₀T² + ^¹ (e^-y1^a -_e^-∕1^b)_e^) + _ς1(t)R1tH*1(t),b1-

^1^{(t) (d}1 ^{- x}o^^{2 +} ^~τ ^{(e y}1^{a -}/1

_e^-M^b)_eM^) + ς1(t)R1tH*1(t)]

.(55)

and

(∣∆_z(t,%o,yo) -∆_f,_m(t,%o,yo)∣∖ _ V∣∣∆∕t,%o,yo) - ∆_p,_m(t,xo,yo)∣/

(μ1^1(t) μ1Φ2(θWlk(O

Vμ2^1(t) μ2^2(t)   l∣y(t)

_-

_-

%_m(0lh y_m(OII∕

yo ∈ C1+ρ2Wd2-yoT²+≤2⅝b ∖                            /2

_-

∕∣∆_f(t,%o,yo) -∆_f,_m(t,%o,yo)∣∖ ≤ ∖∣∆_s(t,xo,yo) -∆_p,_m(t,%o,yo)∣/ ^-

_-

a)) + ς2(t)R2tH*2(t),d1-ρ2(t) (d₂-yoτ²+⅞⅝b-a)) + ς2(t)R2tH*2(t).

/2                ∕

_μc⁺¹(τ) (/-<M^r))

1 Ω1(D.

.(56)

Thus, we conclude that from above vector and also the periodic functions ∆^(t,x_o,y_o) and ∆_g(t,x_o,y_o), ∃ an isolated singular points such that ∆_f(t,x₀,y₀) = 0 and ∆₅(t,Xo,yo) = 0, i. e. the boundary system (1) has periodic solutions x(t, X_o, y_o) and y(t, x_o, y_o).

Proof. Consider the points x₁ and x₂ be defined

in interval,

≤1⅜(e^-y1^a -e^-y1^b)e^y1^τ) + ς√t)R1tH*1(t),b1 - ρ₁(t) (d1

[a1 + ρ1(t) (d1-x₀T² +

^{- x}o^^{2 +}

Theorem 4. Assume that the boundary system (1) is defined on the intervals a ≤ x ≤ b and c ≤ y ≤ d . Then for m ≥ 1 the vector function sequences ∆^,_m(t, x_o,y_o) and ∆g,_m(t,x_o,y_o), which are defined in (27) and (33) satisfy the following inequalities:

≤⅛(e^-y1^a -e^-y1^b)e^y1^τ) + ς₁(t)R₁tH*₁(t)], also y₁ and y₂ be defined in

min a₁+e₁≤x≤b₁-e₁ C1+e2≤y≤d1-e2

max a₁+e₁≤x≤b₁-e₁ C1+e2≤y≤d1-e2

∆∕,_m(t,xo,yo) ≤ -ω_lm

^∆f,m^(t, ^xo,^yo^ ≥ ^1m

interval , c₁ + ρ₂(t) [d₂ - y₀T² + ^² (b ∖                     /2

α)) + ς2(t)R2tH*2(t),d1-ρ2(t) (d2-yoT² + ½J²(b - a)) + ς2(t)R2tH*2(t)],

such that

...(53)

^∆f,m^(t, ^x1,^y1)

^∆f,m^(t, ^x1,^y1)

min a₁+e₁≤x≤b₁-e₁ C1+e2≤y≤d1-e2

max a₁+e₁≤x≤b₁-e₁ C1+e2≤y≤d1-e2

_-

^∆f,m^(t, ^xo, ^yo)

^∆f,m^(t, ^xo, ^yo)

.(57)

∆g,m(t,Xι,yι) =     min    ∆_g,_m(t,x₀,y₀)

• ^a,                 a₁+e₁≤x≤b₁-e₁ ^a

c₁+e₂≤y≤cl₁-e₂

∆g,m(t,X1,y₁) =     max    ∆_g,m(t,x₀,y₀)

• ^a,                 a₁+e₁≤x≤b₁-e₁ ^a

c₁+e2≤y≤d₁-e2

.                                            .„(58)

From the inequalities of system (50), we obtain that

C∆_f(t,x₁,y₁y∖ =

V∆f(t,Xι,yι)) ^

∕         ∆f,m(t,Xι,yι) +

(∆f(t,xι,yι) - ∆f,m(t,xι,yι)) <

^∆f,m^{(t, x}I_iVi) ⁺

∖(∆f(t,Xι,y₁) - ∆f_ιm(t,Xι,y₁)) >

'∆_g(t,Xι,yι') .∆g(t,Xι,yι)

)=

C

∕         ∆g,m(t,Xι,yι) +

(∆g(t, X1,yi) - ∆g,m(t, X1, ∆g,m(t, X1,yi) +

∖(∆g(t, X1,yi) - ∆g,m(t, X₁₁

∖

0

, (59)

∖ 0

, (60)

and from the continuity of the functions ∆f(t,X₀,y₀) and ∆g(t,X₀,y₀) also the inequalities (59) and (60), ∃ an isolated singular points (X⁰,y⁰) = (X₀,y₀), X⁰ ∈ [X1,X2] and y⁰∈[y1,y2] where, ∆f(t,X₀,y₀) and ∆g(t,X₀,y₀) are equal to zeros, thus the boundary system (1) has a solutions X = X(t,X₀,y₀) andy = y(t,X_o,yo).

Remark 1. Theorem 4 is proved when X₀ are y₀ are scalar singular points which should be isolated.

6. CONCLUSIONS

We investigate a solutions for non-linear system of boundary value problems by using the numerical analytic method, which was introduced by Samoilenko, These investigations lead us to improving and extending the above method. Also we expand the results obtained by Samoilenko to change the system of non-linear integro- differential equations with initial condition to a system of non-linear integro- differential equations with boundary conditions.

REFERENCES

Butris, R. N. (1994) Existence of solution for systems of second order differential equations with boundary conditions. J. Education and science, Mosul, Iraq, Vol. 18.

Butris, R. N., & Faris, H. S. (2020) Periodic solutions for nonlinear systems of multiple integro-integral differential equations of (V F) and (F V) type with isolated singular kernels. Gen. Lett. Math., 9(2):106-128.

Butris, R. N., & Faris, H. S. (2020) Solutions for nonlinear systems of integro-differential equations that contain multiple integrals of (V F) and (F V) types with isolated singular kernels. Journal of Xi'an University of Architecture & Technology, 12(5):1541-1553. Gen. Lett. Math., 9(2):106-128.

Ronto, A. & Ronto, M. (2000) On the investigation of some boundary value problems with non- linear conditions. Mathematical Notes, Miskolc, 1(1):43-55.

Samoilenko, A. M., & Rounte, M. I. (1985) Numerical-Analytic Methods for the Investigation of Solutions of BoundaryValue Problems [in Russian]. Naukova Dumka, Kiev.

Samoilenko, A. M., & Rounte, M. I. (1992) Numerical-Analytic Methods in the Theory of Boundary-Value Problems for Ordinary, Differential Equations [in Russian]. Naukova Dumka, Kiev.

Zavizion, G. V. (2009) Periodic solutions of integro-differential equations. J. of Diff. Equations, 45(2):240-248.

Zill, D. G. & Warren, S. W. (2013) Differential equations with boundary value problems. Section 7.4: Operational Properties II., Pp. 305.

259