Kompresi Citra Medis dengan DWT dan Variable Length Code
on
Majalah Ilmiah Teknologi Elektro, Vol. 20, No. 2, Juli - Desember 2021
DOI: https://doi.org/10.24843/MITE.2021.v20i02.P02 187
Kompresi Citra Medis dengan DWT dan Variable Length Code
I Gusti Ayu Garnita Darma Putri 1 , I Made Oka Widyantara 2 , Nyoman Putra Sastra3 , Dewa Made Wiharta.4
[Submission: 10-03-2021, Accepted: 07-05-2021]
Abstract— Medical images contain a lot of important information such as patient and examination data. Therefore, medical images have large file sizes and thus require longer transmission times, larger data storage, and high computation. Hence, medical images require digital image compression techniques that can reduce file size while preserving the important information. This paper designed a medical image compression scheme using DWT with mother wavelet Coiflet and Symlet. Thresholding and quantization process are the key to lossy compression in this scheme, and the outputs will be coded with Huffman or Arithmetic coding. There are four different codec combinations namely: Coiflet-Huffman, Coiflet-Arithmetic, Symlet-Huffman, Symlet-Arithmetic. Compression performance of each codec will be analyzed based on PSNR and compression ratio. The compression testing used 3 grayscale medical images with dimension of 160x160 pixels. The most optimal PSNR and rate are produced by Symlet-Aritchmetic codec with recommendation threshold value less than 12. Threshold value above 12 causes PSNR of the reconstruction image will be below the minimum PSNR stardard for digital image, which is of 30dB. The scheme is expected to be a media for processing medical image data in telemedicine applications because can reduce the size of medical images but still maintain visual quality.
Intisari— Citra medis mengandung banyak informasi penting seperti data pasien serta data pemeriksaan, sehingga memiliki ukuran file yang besar. Hal ini menyebabkan citra medis membutuhkan waktu transmisi lebih panjang, penyimpanan data lebih besar, dan komputasi yang relatif tinggi. Oleh karena itu, diperlukan teknik kompresi citra yang mampu mengurangi ukuran file namun tetap menjaga informasi penting yang terkandung dalamnya. Untuk itu, pada paper ini dirancang sebuah skema kompresi citra medis menggunakan DWT dengan wavelet Coiflet dan Symlet. Proses thresholding dan kuantisasi menjadi kunci terjadinya lossy compression di skema ini, dan data outputnya akan dikodekan dengan pengkodean Huffman atau Arithmetic. Terdapat empat kombinasi codec berbeda yaitu: Coiflet-Huffman, Coiflet-Arithmetic, Symlet-Huffman dan Symlet-Arithmetic yang masing-masing dianalisis kinerja kompresinya berdasarkan PSNR dan rasio kompresi. Pengujian kompresi menggunakan 3 citra medis grayscale berdimensi 160x160 piksel. Hasil pengujian menunjukan codec yang mampu menghasilkan PSNR dan rate paling optimal adalah codec Symlet-Arithmetic dengan nilai threshold yang dianjurkan kurang dari 12.
Pemberian nilai threshold diatas 12 menyebabkan PSNR citra rekonstruksi berada dibawah standar nilai minimum PSNR citra digital sebesar 30 dB. Skema pada paper ini diharapkan mampu menjadi media pengolahan data citra medis dalam aplikasi telemedicine karena mampu menurunkan ukuran citra medis namun tetap dapat menjaga kualitas secara visual.
Kata Kunci— kompresi, citra medis, PSNR, rate, Symlet, Coiflet, Huffman, Arithmetic.
-
I. pendahuluan
Citra medis merupakan penggambaran bagian dalam tubuh manusia yang bertujuan untuk mengetahui kondisi organ tertentu secara non-invasive [1]. Citra medis yang banyak ditemui adalah CT (Computed Tomography) Scanning, MRI (Magnetic Resonance Imaging), USG (Ultrasonografi), X-Ray ataupun PET (Positron Emission Tomography) yang umumnya masih berupa data analog. Namun, saat ini banyak citra medis yang sudah digitalisasi dengan mengacu pada standar DICOM.
Digital Imaging and Comunication in Medicine (DICOM) adalah standar komunikasi dan pencitraan yang digunakan dalam pengembangan aplikasi medis untuk mendukung proses pendistribusian dan proses review citra medis. DICOM menspesifikasikan suatu Information Object Definition (IOD) yang memodelkan semua informasi terkait proses pencitraan medis. IOD mengandung entitas informasi yaitu entitas pasien yang berisi data pasien serta entitas studi yang berisi informasi pemeriksaan [1].
Citra medis banyak mengandung informasi penting sehingga memiliki ukuran file yang besar. Ukuran file yang tergolong cukup besar ini tentunya membutuhkan sumber daya besar yang digunakan untuk mengolah, mengirimkan, dan menyimpan citra medis tersebut. Oleh sebab itu, diperlukan teknik kompresi citra digital yang mampu mengurangi ukuran file citra namun tetap menjaga kualitas citra medis dan informasi penting didalamnya.
Redundansi suatu informasi dengan tetap menjaga kualitas penggambaran informasi dapat dihilangkan dengan teknik kompresi. Ada dua model teknik kompresi citra, yakni lossless compression yang menghasilkan citra kompresi tepat sama dengan citra aslinya, dan lossy compression yang mampu memberikan visualisasi citra kompresi yang mirip dengan citra aslinya namun sebenarnya terdapat beberapa bagian atau informasi yang dihilangkan [2].
Banyak penelitian yang dikembangkan terkait kompresi citra medis [3] - [5]. Salah satunya dengan transformasi wavelet yang digunakan pada standar JPEG2000 dan sudah didukung oleh DICOM [6]. Transformasi wavelet adalah metode yang didasarkan pada konvolusi sinyal ke filter tertentu dan mendekomposisikan sinyal tersebut kedalam beberapa komponen dengan skala berbeda-beda [7], [8]. Refrensi [9]
… p-ISSN:1693 – 2951; e-ISSN: 2503-2372

membandingkan 50 citra medis BMP dan 100 citra medis JPG yang dikompresi dengan wavelet Daubechies, Haar dan Symlets pada 3 level dekomposisi. Refrensi [10] mengkompresi citra medis menggunakan packet wavelet transform (PWT) dan run length encoding (RLE) dengan dengan 3 threshold yaitu tiga puluh (30), empat puluh (40), dan dan lima puluh (50). Sedangkan penelitian [11] menggunakan threshold yang bersifat adaptive.
Pada paper ini dirancang sebuah skema kompresi citra medis menggunakan DWT dengan mother wavelet Coiflet dan Symlet karena lebih tahan terhadap noise [12] - [14]. Kemudian dilakukan proses thresholding dan kuantisasi yang menjadi kunci terjadinya lossy compression. Selanjutnya data output akan dikodekan dengan Huffman atau Arithmetic. Pemilihan kedua teknik pengkodean ini karena persamaan karakteristiknya yang mengkodekan jumlah bit berdasarkan probabilitas kemunculan (variable length code). Skema ini menghasilkan empat kombinasi codec berbeda yakni: Coiflet-Huffman, Coiflet-Arithmetic, Symlet-Huffman, Symlet-Arithmetic. Kemudian dilakukan analisis untuk mengetahui kinerja kompresi pada masing-masing codec.
Penelitian ini dapat dijadikan alternatif lossy image compression codec dengan kombinasi beberapa mother wavelet serta pengkodean berbasis variable length code disertai dengan rekomendasi nilai threshold yang optimal. Perbedaan antara penelitian ini dengan penelitian yang sudah dilakukan sebelumnya yakni dengan melakukan analisa kiberja kompresi beberapa kombinasi codec berbeda pada nilai threshold berbeda serta analisa pengaruh mother wavelet dan teknik pengkodean terhadap hasil kompresi. Skema kompresi citra medis ini diharapkan mampu menjadi media pengolahan data citra medis dalam aplikasi telemedicine karena mampu menurunkan ukuran atau kapasitas data hasil kompresi namun tetap dapat menjaga kualitas secara visual.
Paper ini selanjutnnya akan terdiri dari 5 bagian, yaitu pada bagian ke-2 menjelaskan teori mengenai DWT dan pengkodean Huffman serta Arithmetic, bagian ke-3 menjelaskan tentang skema kompresi citra medis secara umum dan alur rancang bangun codec yang dibuat, bagian ke-4 memaparkan hasil pengujiann dan analisis kinerja kompresi yang dilakukan pada setiap codec, dan bagian ke-5 berisi kesimpulan dan saran
-
II. DWT Serta Teknik Pengkodean Huffman dan Arithmetic
-
B. DWT (Discrete Wavelet Transform)
Discrete wavelet transforms merupakan dekomposisi frekuensi subband citra dengan cara penurunan level dekomposisi. Teknik filter digital merupakan penggambaran skala waktu sinyal digital dalam DWT dengan menggunakan filter digital. Filter digital akan melewatkan sinyal dengan frekuensi dan skala yang berbeda. Resolusi sinyal yang merupakan rata-rata jumlah detil informasi dalam sinyal ditentukan melalui filterisasi, sedangkan skalanya diperoleh melalui proses downsampling (subsampling) dan upsampling [15]
Frekuensi sinyal dianalisis dengan melewatkan sinyal pada dua filter DWT, yaitu lowpass filter dan highpass filter.
Analisis frekuensi rendah mennggunakan lowpass filter, sedangkan frekuesi tinggi dengan highpass filter. Analisis frekuensi dilakukan pada resolusi yang dihasilkan ketika sinyal melewati filterisasi DWT. Analisis pada resolusi berbeda ini disebut multi-resolution analysis [15], [16].
Sinyal dibagi menjadi dua frekuensi berbeda pada transformasi wavelet, yaitu frekuensi tinggi dan rendah. Lowpass filter adalah fungsi penyekalaan (scaling function), sedangkan high pass filter untuk fungsi wavelet (wavelet function) [16]. Downsampling pada hasil filterisiasi untuk menghasilkan citra low pass dan high pass. Pembagian dilanjutkan, yaitu frekuensi rendah yang dihasilkan dibagi kembali menjadi dua frekuensi berbeda, frekuensi tinggi dan rendah. Jika didekomposisi tidak dapat dilakukan lagi maka proses akan dihentikan [17].
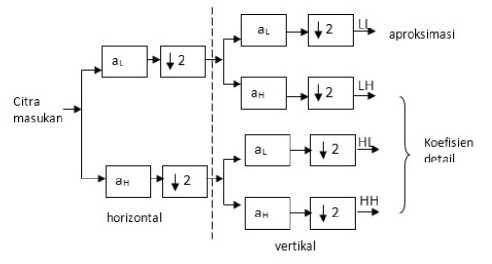
Gambar 1: Proses Dekomposisi DWT
Dari Gambar 1, terlihat bahwa dekomposisi DWT dua dimensi pada satu level menghasilkan empat sub-band, yaitu: koefisien aproksimasi (sub-band LL), koefisien detail vertikal (sub-band LH), koefisien detail horizontal (sub-band HL) dan koefisien detail diagonal (sub-band HH). Downsampling dilakukan pada tanda panah ke bawah, panjang aL menjadi setengah kali dari panjangnya semula [17].
Transformasi diawali dengan pemindaian citra secara horizontal pada lowpass filetering (L), hasilnya adalah koefisien aL. Dilanjutkan dengan pemindaian pada highpass filtering (H) untuk menghasilkan koefisien aH. Setiap koefisien aL dan aH akan mengalami downsampling. Pemindaian berikutnya secara vertikal, dengan L dan H, serta downsampling dilakukan kembali pada koefisen yang dihasilkan pada tahap sebelumnya, hasilnya adalah LL, LH, HL, dan HH. Dekomposisi dapat dilakukan diberbagai level subband dengan ukuran satu level dekomposisi adalah seperempat dari ukuran sub-band sebelumnya. LL1, LH1, HL1 dan HH1 merupakan hasil dari dekomposisi level 1, untuk level selanjutnya dilakukan dekomposisi hanya pada sub-band aproksimasi saja [16], [18]. Sebagai contoh, dekomposisi level 2 ditunjukkan pada Gambar 2.
|
LL1LL2 |
LL1HL2 |
HL |
|
LL1LH2 |
LL1HH2 | |
|
LH |
HH | |
DOI: https://doi.org/10.24843/MITE.2021.v20i02.P02
Gambar 2: Dekomposisi Level 2
Rekonstruksi dengan menerapkan Inverse Discrete Wavelet Transform (IDWT) merupakan proses pemulihan kembali sinyal hasil dekomposisi. Koefisien aproksimasi mengalami upsampling dan dikonvolusi dengan invers low pass filter dan high pass filter yang digunakan. Proses rekontruksi adalah
Penelitian ini mengggunakan jenis wavelet Coiflet dan Symmetrics Wavelet (Symlet) yang dijelaskan sebagai berikut
-
1) Coiflet: Filter Coiflet merupakan salah satu bagian dari orthogonal wavelet yang akan mengubah data input menjadi lebih singkat [19], [20]. Karakteristik dari filter Coiflet ditunjukan pada Tabel 1.
TABEL I karakteristik filter Coiflet
|
Keluarga wavelet |
Coiflet |
|
Nama Singkat |
Coif |
|
Orde N |
N = 1, 2, …, 5 |
|
Contoh |
Coif1, …, coif5 |
|
Orthogonal |
Ya |
|
Biorthogonal |
Ya |
|
DWT |
Memungkinkan |
|
CWT |
Memungkinkan |
|
Lebar Pendukung |
6N-1 |
|
Panjang Filter |
6N |
|
Jumlah vanishing moment pada phi |
2N |
|
Jumlah vanishing moment pada psi |
2N-1 |
-
2) Symlet: Filter Symlet merupakan modifikasi dari Daubechies untuk meningkatkan simetris filter Daubechies. Symlet (symmetrics wavelet) di design agar memiliki sedikit bentuk asimetris dan nilai yang tinggi untuk vanishing moment yang bersifat singkat atau pendek [21], [22]. Karakteristik dari filter Symlet ditunjukan pada Tabel 2.
189 keabuan dengan frekuensi kemunculan yang tinggi pada sebuah citra dikodekan dengan jumlah bit yang lebih pendek, sedangkan nilai dengan frekuensi kemunculannya rendah dikodekan menjadi jumlah bit yang lebih panjang. Pengkodean Huffman memetakan panjang blok keluaran sumber ke blok biner berdasarkan pajang variable. Proses pemetaan ini disebut fixed to variable-length coding. Ide dasar pengkodean Huffman adalah memetakan dari simbol dengan jumlah kemunculan paling banyak sampai paling jarang pada sebuah urutan sumber menjadi urutan biner [23], [24].
Algoritma pengkodean Huffman untuk kompresi citra dijabarkan sebagai barikut:
Algoritma 1
-
a. Ubah data citra dari bentuk matriks menjadi vektor
-
b. Tentukan jumlah kemunculan setiap warna atau derajat keabuan
-
c. Urutkan dari rendah ke tinggi frekuensi munculnya piksel pada sebuah citra. Setiap nilai dinyatakan sebagai pohon bersimpul tunggal.
-
d. Gabungkan dua buah pohon dengan frekuensi kemunculan terendah pada sebuah akar.
-
• Probabilitas akar adalah jumlah peluang kemunculan dua pohon penyusunnya.
-
• Frekuensi kemunculan lebih rendah ditempatkan di sisi kiri dengan bobot 0, sedangkan sisi kanan bobot 1
-
e. Langkah (d) diulang, sampai mennyisakan 1 pohon biner
-
f. Pohon biner ditelusuri dari akar ke daun. Deretan bobot sisi dari akar ke daun merupakan kode Huffman untuk derajat keabuan atau warna yang bersesuaian.
-
g. Ganti data dengan kode Huffman yang bersesuaian.
TABEL III
KARAKTERISTIK FILTER SYMLET
|
Keluarga wavelet |
Coiflet |
|
Nama Singkat |
Coif |
|
Orde N |
N = 1, 2, …, 5 |
|
Contoh |
Coif1, …, coif5 |
|
Orthogonal |
Ya |
|
Biorthogonal |
Ya |
|
DWT |
Memungkinkan |
|
CWT |
Memungkinkan |
|
Lebar Pendukung |
6N-1 |
|
Panjang Filter |
6N |
|
Jumlah vanishing moment pada phi |
2N |
|
Jumlah vanishing moment pada psi |
2N-1 |
-
C. Pengkodean Huffman
Judul Huffman merupakan lossless compression yang didasarkan pada derajat keabuan (gray level) atau tingkat warna piksel-piksel yang terdapat pada citra. Warna atau derajat
-
h. Simpan data lebar, tinggi, kode bit untuk tiap nilai, nilai derajat keabuan, dan data citra yang sudah dikodekan ke dalam file hasil kompresi
-
D. Pengkodean Arithmetic
Arithmetic coding memberikan range atau interval pada setiap simbol antara nol sampai satu. Setiap range dibagi menjadi beberapa sub-range yang ukurannya sebanding dengan probabilitas. Semakin tinggi probabilitas suatu simbol, maka semakin tinggi pula range yang diberikan terhadap simbol tersebut. Pengkodean Arithmetic mengubah sebuah deret simbol input menjadi bilangan floating point. Semakin kompleks dan panjang pesan yang dikodekan, bit yang diperlukan untuk pengkodean semakin banyak. Output pengkodean Arithmetic adalah sebuah angka yang nilainya kurang dari satu dan lebih dari atau sama dengan nol. Angka ini di-decode-kan untuk menghasilkan deretan simbol yang dipakai untuk menghasilkan angka tersebut. Untuk menghasilkan angka output tersebut, tiap simbol yang akan diencode diberi satu set nilai probabilitas [25], [26].
I Gusti Ayu Garnita Darma Putri: Metode Kompres Citra Medis…
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

Algoritma proses kompresi menggunakan pengkodean Arithmetic adalah sebagai berikut.
Algoritma 2
Cari peluang dari tiap karakter pada teks yang akan dikodekan
Tetapkan nilai low_int(0)=0 high_int(0)=1 range_int(0)=1
while not EOF (fin), baca karakter ke-i do
low(i)=low_int(i1)+range_int(i1)*low_symbol. …………………………………………………………………………………………………………… (1)
high(i)=low_int(i–1)+range_int(i-1)
*high_symbol………………………………………………………………………………(2) low_int(i)=low(i) ………………………………………………………………(3) high_int(i)=high(i) …………………………………………………………(4) range_int(i)=high(i)-low(i) ……………………………………(5) return
Algoritma dekompresi citra untuk pengkodean Arithmetic adalah sebagai berikut.
Algoritma 3
output(0)=nilai hasil kompresi while output(i)!=0 do
output(i) =
return
(output (i-l)-low symbol) (high symbol-low symbol)
(6)
-
III. Skema Kompresi Citra Medis
-
A. Skema Umum
Proses kompresi citra menggunakan DWT ditunjukkan pada Gambar 3. Kompresi diawali dengan menginputkan citra asli, melalui sebuah teknik scanning sehingga dapat ditampilkan dalam bentuk matriks yang mewakili nilai derajat keabuan tiap piksel. Matriks tersebut didekomposisikan dengan melakukan downsampling, selanjutnnya dilewatkan pada dua jenis filter digital. Low pass filter digunakan untuk menganalisis data berfrekuensi rendah, sedangkan high pass filter menganalisis data berfrekuensi tinggi.
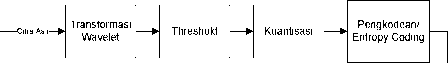
CtraHasii _ Transformasi
Rekonstruksi Wavelet Balik
Invers Kuantisasi
DekodeZEntropy Coding
Data Hasil Kompresi
Gambar 3: Proses Kompresi Citra Medis dengan Transformasi Wavelet
Koefisien filter yang digunakan tergantung pada jenis mother wavelet yang dipilih. Dari proses filterisasi tersebut dihasilkan sebuah matriks transformasi baru. Matriks ini selanjutnya diberikan threshold, yaitu data dengan nilai kurang dari threshold akan diubah menjadi nol. Nilai matriks keluaran thresholding diubah sesuai dengan level atau rentang yang
ditetapkan, proses ini disebut sebagai kuantisasi. Matriks hasil kuantisasi dikodekan menggunakan entropy coding sehingga representasi data yang baru memiliki ukuran lebih kecil dibandingkan dengan data citra awal. Untuk tahap dekompresi, inputan berupa data hasil kompresi yang kemudian didekodekan dengan teknik yang sama pada saat pengkodean. Nilai yang diperoleh dikembalikan menjadi rentang awal menggunakan inverse kuantisasi, selanjutnya direkonstruksi dengan inverse wavelet.
-
B. Alur Kompresi Citra Medis
Gambar 4 merupakan metode kompresi citra medis yang digunakan pada penelitian ini. Metode ini diawali dengan proses menginputkan citra medis, selanjutnya dilakukan pemindaian untuk membaca nilai derajat keabuan pada setiap piksel citra. User menginputkan jenis mother wavelet, level dekomposisi, threshold dan entropy coding yang digunakan. Inputan tersebut akan dibaca dan diolah oleh sistem sesuai algoritma yang diterapkan. Jika user memilih mother wavelet Coiflet, citra asli akan ditransformasikan menggunakan filter Coiflet. Jika tidak, citra asli ditransformasi menggunakan filter Symlet. Banyaknya proses dekomposisi yang terjadi pada transformasi citra sesuai dengan level dekomposisi yang dimasukkan oleh user. Data citra hasil transformasi yang bernilai lebih rendah dari threshold diubah menjadi bernilai nol. Data hasil thresholding ini akan dikuantisasi dan dikodekan dengan salah satu teknik entropy coding. Jika user memilih teknik Huffman, data citra akan dikodekan dengan menggunakan Huffman. Jika tidak memilih teknik Huffman, data citra dikodekan menggunakan teknik Arithmetic. Output akhir berupa sebuah matriks compression code yang dijadikan sebagai rate hasil kompresi encoder
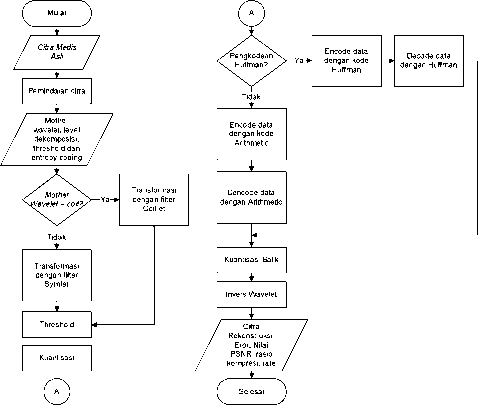
Gambar 4: Diagram Alir Kompresi Citra Medis Menggunakan DWT dengan Pengkodean Huffman dan Arithmetic
Langkah pertama pada decoder adalah mendekodekan data kompresi sesuai dengan teknik entropy coding yang dipilih sebelumnya. Jika pada kompresi digunakan teknik Huffman,
DOI: https://doi.org/10.24843/MITE.2021.v20i02.P02
proses dekode juga menggunakan teknik Huffman. Jika tidak menggunakan teknik Huffman akan digunakan teknik Arithmetic. Setelah proses dekode selesai, matriks tersebut akan dikuantisasi balik untuk mendapatkan kembali nilai matriks asli yang sama seperti sebelum proses kuantisasi pada encoder. Data transformasi inilah yang akan direkonstruksi menggunakan invers filter mother wavelet. Proses rekonstruksi tergantung pada mother wavelet yang dipilih saat kompresi, jika mother wavelet yang dipilih adalah Coif, citra direkonstruksi dengan menggunakan inverse filter Coiflet. Jika dipilih Sym, citra direkontruksi dengan inverse filter Symlet. Hasil rekonstruksi inilah yang merupakan citra hasil dekompresi atau citra rekontruksi yang nantinya akan dianalisa rasio kompresi dan kualitasnya
-
C. Parameter Pengukuran Kinerja Kompresi
Parameter pengukuran kinerja kompresi citra merujuk pada PSNR dan rasio kompresi
-
1) PSNR (Peak Signal to Noise Ratio): PSNR merupakan metode pengukuran perbedaan citra asli dengan citra hasil kompresi dengan rumus:
PSNR = 20 x log10 (^^).................................. (7)
191 mengindikasi bahwa proses kompresi berjalan dengan efektif. Nilai rasio kompresi yang besar dengan kualitas citra yang terjaga merupakan target dalam suatu teknik kompresi citra.
-
IV. Hasil dan Pembahasan
Skema kompresi citra medis ini diujikan dengan empat codec berbeda untuk dianalisis kinerja kompresinya. Codec yang digunakan yakni:
-
• Transformasi Coiflet dengan pengkodean Huffman
-
• Transformasi Coiflet dengan pengkodean Arithmetic
-
• Transformasi Symlet dengan pengkodean Huffman
-
• Transformasi Symlet dengan pengkodean Arithmetic.
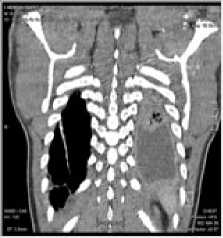
Nilai threshold dan level dekomposisi memiliki pengaruh terhadap kinerja kompresi, semakin besar kedua nilai tersebut maka semakin banyak informasi yang dihilangkan. Hal ini dapat menurunkan kualitas citra, walaupun rasio kompresi yang dihasilkan semakin baik. Untuk itu, pada penelitian ini digunakan level dekomposisi bernilai 2 dan nilai threshold bernilai 6, 9, 12, dan 15 dengan arsitektur codec mengacu pada Gambar 4. Citra uji yang digunakan pengujian adalah citra medis grayscale berdimensi 160x160 piksel, citra uji 1 dan citra uji 3 merupakan hasil CT-Scan dan citra uji 2 merupakan hasil X-Ray yang diunduh di https://www.adamimages.com/
dengan b adalah nilai sinyal tertinggi (pada citra grey scale, b=255). Sedangkan MSE merupakan akar pangkat dua selisih antara citra asli dengan citra hasil kompresi. Perhitungan mse dengan cara sebagai berikut:
MSE =
1
Lebar × Tinggi
∑ ∑ (fjj- Z^
i=1 J=1
(8)
dimana, f dan f’ merupakan nilai piksel citra asli dan nilai piksel citra rekonstruksi.
PSNR memiliki satuan decibel (dB) dan hanya dapat dihitung setelah proses dekompresi citra. PSNR berbanding terbalik dengan MSE, jika nilai MSE rendah maka PSNR akan bernilai tinggi yang berarti citra rekonstruksi memiliki kualitas yang baik dan mendekati citra asli. Semakin besar nilai PSNR, semakin bagus kualitas kompresi. Nilai PSNR untuk kompresi lossy antara 30dB sampai 50 dB [2], [10].
2) Rasio Kompresi: Salah satu parameter untuk mengukur kinerja suatu proses kompresi adalah rasio kompresi. Citra asli atau citra sebelum dikompresi akan dibandingkan dengan hasil kompresi [2], [27]. Persamaan matematis rasio kompresi adalah sebagai berikut:
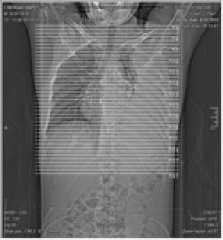

(a) Citra Uji 1 (b) Citra Uji 2
A rasio kompresi = -.........................................(9)
dengan:
A = Ukuran citra asli
B = Ukuran citra kompresi
Ukuran citra hasil kompresi berbanding terbalik dengan rasio kompresi, semakin kecil ukuran citra hasil kompresi maka akan menghasilkan rasio kompresi yang besar dan
(c) Citra Uji 3
Gambar 5: Citra Medis yang Digunakan dalam Skema Kompresi
Ketiga citra uji ini dipilih karena memiliki karakteristik yang berbeda-beda berdasarkan nilai histogramnya seperti ditunjukkan Gambar 6. Grafik histogram merepresentasikan distribusi nilai intensitas warna dari citra uji [27]. Sumbu horizontal menampilkan rentang nilai piksel citra dari 0 sampai 255, sedangkan sumbu vertikal menunjukkan jumlah
I Gusti Ayu Garnita Darma Putri: Metode Kompres Citra Medis…
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

kemunculan nilai piksel. Citra uji 2 memiliki informasi penting yang lebih sedikit dibandingkan citra uji lain karena pikselnya dominan bernilai rendah (mendekati 0) sehingga cenderung berwarna kehitaman. Sebaliknya, citra uji 3 mengandung
paling banyak informasi penting karena memiliki banyak
variasi nilai piksel yang tinggi (mendekati 255).
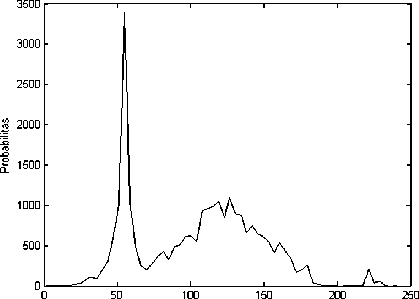
Nilai Piksel
(a) Histogram Citra Uji 1
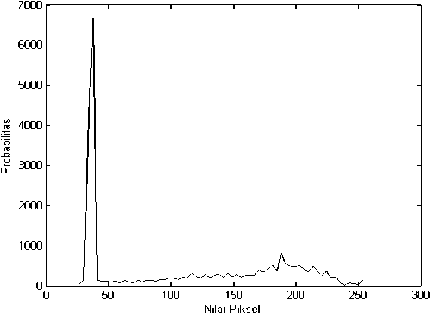
(b) Histogram Citra Uji 2
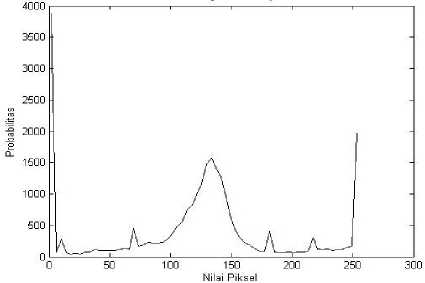
(c) Histogram Citra Uji 3 Gambar 6: Grafik Histogram Citra Uji
Tabel 3, Tabel 4, dan Tabel 5 menunjukkan hasil pegujian pengaruh nilai threshold terhadap kinerja kompresi setiap codec pada masing-masing citra uji. Thresholding merupakan pengabaian koefisien hasil transformasi yang dianggap tidak mengandung cukup informasi penting dengan mengubah
koefisien yang memiliki nilai dibawah nilai threshold menjadi nol. Semakin besar nilai threshold maka jumlah koefisien yang mengalami threholding juga ikut meningkat yang dapat dibuktikan dari besarnya nilai persentase thresholding (%TH). Persentase koefisien thresholding (%TH) adalah jumlah koefisien yang mengalami threholding dari total semua koefisien.
TABEL III
hasil pengujian kompresi citra uji 1
|
Codec |
TH |
%TH |
Kompresi |
PSNR (dB) | |
|
Rate (kB) |
Rasio (%) | ||||
|
Coiflet-Huffman |
6 |
57.15 |
13.14 |
23.78 |
41.23 |
|
9 |
64.66 |
11.81 |
26.46 |
35.40 | |
|
12 |
69.72 |
10.83 |
28.87 |
31.12 | |
|
15 |
73.30 |
10.13 |
30.86 |
27.77 | |
|
Coiflet-Arithmetic |
6 |
57.15 |
13.03 |
23.98 |
41.23 |
|
9 |
64.66 |
11.53 |
27.10 |
35.40 | |
|
12 |
69.72 |
10.36 |
30.17 |
31.12 | |
|
15 |
73.30 |
9.49 |
32.94 |
27.77 | |
|
Symlet-Huffman |
6 |
57.36 |
12.81 |
24.40 |
41.62 |
|
9 |
64.50 |
11.67 |
26.77 |
35.86 | |
|
12 |
69.13 |
10.84 |
28.83 |
31.60 | |
|
15 |
72.40 |
10.19 |
30.68 |
28.30 | |
|
Symlet-Arithmetic |
6 |
57.36 |
12.69 |
24.62 |
41.62 |
|
9 |
64.50 |
11.40 |
27.40 |
35.86 | |
|
12 |
69.13 |
10.41 |
30.01 |
31.60 | |
|
15 |
72.40 |
9.61 |
32.51 |
28.30 | |
TABEL IV hasil pengujian kompresi citra uji 2
|
Codec |
TH |
%TH |
Kompresi |
PSNR (dB) | |
|
Rate (kB) |
Rasio (%) | ||||
|
Coiflet-Huffman |
6 |
79.32 |
8.57 |
36.46 |
43.79 |
|
9 |
82.46 |
8.04 |
38.89 |
40.34 | |
|
12 |
84.31 |
7.69 |
40.61 |
37.55 | |
|
15 |
85.59 |
7.42 |
42.09 |
35.45 | |
|
Coiflet-Arithmetic |
6 |
79.32 |
7.55 |
41.38 |
43.79 |
|
9 |
82.46 |
6.77 |
46.14 |
40.34 | |
|
12 |
84.31 |
6.27 |
49.88 |
37.55 | |
|
15 |
85.59 |
5.88 |
53.17 |
35.45 | |
|
Symlet-Huffman |
6 |
79.16 |
8.31 |
37.62 |
45.99 |
|
9 |
82.49 |
7.72 |
40.49 |
41.74 | |
|
12 |
84.32 |
7.42 |
42.10 |
38.53 | |
|
15 |
85.41 |
7.18 |
43.55 |
36.27 | |
|
Symlet-Arithmetic |
6 |
79.16 |
7.34 |
42.60 |
45.99 |
|
9 |
82.49 |
6.50 |
48.11 |
41.74 | |
|
12 |
84.32 |
6.05 |
51.66 |
38.53 | |
|
15 |
85.41 |
5.71 |
54.74 |
36.27 | |
Nilai PSNR terbaik setiap codec berada pada threshold 6 dan mengalami penurunan seiring pertambahan nilai threshold. Semakin besar nilai threshold, kualitas citra semakin menurun karena lebih banyak informasi yang dihilangkan sehingga nilai
DOI: https://doi.org/10.24843/MITE.2021.v20i02.P02
PSNR menjadi lebih kecil. Dari ketiga tabel hasil pengujian terlihat bahwa threshold bernilai 15 menyebabkan PSNR citra rekonstruksi berada dibawah standar nilai minimum PSNR citra digital sebesar 30 dB [10]. Sedangkan pada Tabel 5, kompresi dengan threshold 12 sudah menyebabkan PSNR di bawah standar, oleh sebab itu nilai threshold yang dianjurkan adalah kurang dari 12.
TABEL v
hasil pengujian kompresi citra uji 3
|
Codec |
TH |
%TH |
Kompresi |
PSNR (dB) | |
|
Rate (kB) |
Rasio (%) | ||||
|
Coiflet-Huffman |
6 |
46.46 |
14.86 |
21.03 |
39.43 |
|
9 |
55.66 |
13.24 |
23.61 |
33.76 | |
|
12 |
61.76 |
12.38 |
25.25 |
29.50 | |
|
15 |
66.31 |
11.54 |
27.07 |
26.15 | |
|
Coiflet-Arithmetic |
6 |
46.46 |
14.77 |
21.16 |
39.43 |
|
9 |
55.66 |
13.17 |
23.73 |
33.76 | |
|
12 |
61.76 |
12.17 |
25.67 |
29.50 | |
|
15 |
66.31 |
11.21 |
27.89 |
26.15 | |
|
Symlet-Huffman |
6 |
45.96 |
14.63 |
21.36 |
39.75 |
|
9 |
55.08 |
13.14 |
23.79 |
34.09 | |
|
12 |
61.26 |
12.20 |
25.62 |
29.67 | |
|
15 |
65.67 |
11.39 |
27.43 |
26.27 | |
|
Symlet-Arithmetic |
6 |
45.96 |
14.54 |
21.50 |
39.75 |
|
9 |
55.08 |
13.06 |
23.94 |
34.09 | |
|
12 |
61.26 |
12.03 |
25.98 |
29.67 | |
|
15 |
65.67 |
11.10 |
28.16 |
26.27 | |
Nilai threshold berbanding lurus dengan rasio kompresi, dimana nilai rasio kompresi terbaik semua codec ada di threshold 15. Semakin besar nilai threshold, maka koefisien citra yang mengalami thresholding semakin bertambah dan nilai persentasi thresholding (%TH) meningkat, sehingga ukuran data hasil kompresi (rate) semakin kecil. Hal ini lah yang menyebabkan terjadinya peningkatan nilai rasio kompresi.
-
A. Analisa Rate Distortion
Gambar 6, Gambar 7, dan Gambar 8 merupakan grafik yang menunjukkan hubungan antara rate dan PSNR setiap codec. Dari ketiga grafik tersebut, maka dapat dilihat bahwa bahwa codec dengan transformasi Symlet menghasilkan nilai PSNR yang lebih besar dibandingkan dengan codec Coiflet. Hal ini karena filter sym5 adalah wavelet biorthogonal atau simetris yang mampu mereduksi noise jika dibandingkan dengan filter coif2 yang merupakan wavelet orthogonal [27], [28].
Nilai PSNR codec Coiflet-Huffman sama dengan PSNR Coiflet-Arithmetic, sedangkan nilai PSNR Symlet-Huffman sama dengan PSNR Symlet-Arithmetic. Codec dengan jenis wavelet yang sama akan menghasilkan nilai PSNR yang sama. Perbedaan teknik pengkodean yang digunakan lebih berpengaruh pada rasio kompresi yang dihasilkan karena pengkodean Huffman dan Arithmatic bersifat lossless.
193
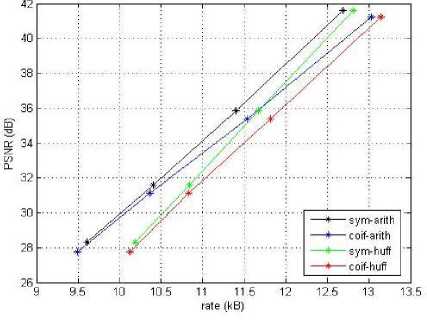
Gambar 7: Grafik Rate Distortion Citra Uji 1
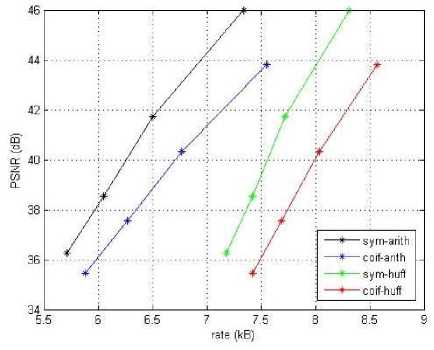
Gambar 8: Grafik Rate Distortion Citra Uji 2
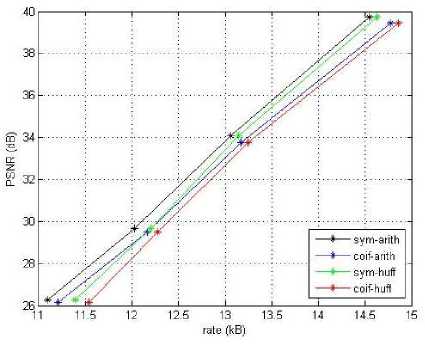
Gambar 9: Grafik Rate Distortion Citra Uji 3
Penggunaan pengkodean Arithmetic menyebabkan data rate menjadi lebih rendah dibandingkan pengkodean Huffman. Huffman mengkodekan setiap koefisien ke dalam bit yang panjangnya tergantung dari probabilitas kemunculan koefisien tersebut, sedangkan Arithmetic hanya mengkodekan output terakhir hasil komputasi aritmatika yang digunakan sebagai data hasil kompresi.
I Gusti Ayu Garnita Darma Putri: Metode Kompres Citra Medis…
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

-
V. Kesimpulan dan Saran
Pada paper ini, telah dirancang dan direalisasikan sebuah skema atau codec untuk mengkompresi citra medis menggunakan DWT dengan teknik pengkodean Huffman dan Arithmetic yang bertujuan untuk memperoleh besar rate lebih optimal namun dapat tetap mempertahankan kualitas citra rekonstruksi. Hasil pengujian menunjukan bahwa codec yang mampu menghasilkan PSNR dan rate paling optimal adalah codec Symlet-Arithmetic dengan nilai threshold yang dianjurkan yakni kurang dari 12. Pemberian nilai threshold di atas 12 akan menyebabkan PSNR citra rekonstruksi berada dibawah standar nilai minimum PSNR citra digital sebesar 30 dB.
Referensi
-
[1] C.M. Karyati, S. Widiyanto, A. Muslim, R.J.Suhatril. (2013) Analisa dan Pengolahan Citra Medis (Segmentasi …). [Online]. Available: http://ebook.gunadarma.ac.id/informatika/111/
-
[2] Sutoyo, T., Mulyanto, E., Suhartono, V., Nurhayati, O. D. & Wijanarto (2009). Teori pengolahan citra digital. Andi: Yogyakarta.
-
[3] A. M. Faza, C. Slamet, D. Nursantika, “Analisis Kinerja Kompresi Citra Digital dengan Komparasi DWT, DCT dan Hybrid (DWT-DCT)”, Jurnal Online Informatika, vol. 1 no. 1, pp. 1-5, Jun. 2016
-
[4] H. Amri, A. Khalfallah, M. Gargouri, N. Nebhani, J.C. Lapayre, M.S. Bouhlel, “Medical Image Compression Approach Based on Image Resizing, Digital Watermarking and Lossless Compression”, Journal of Signal Processing Systems, vol. 87, pp. 203-2014, Jul. 2017
-
[5] H. Sunil, Sharanabasaweshwar, G. Hiremath, “A combined scheme of pixel and block level splitting for medical image compression and reconstruction”, Alexandria Engineering Journal, vol. 57, pp. 767-772, Jun. 2018
-
[6] S. UmaMaheswari, V. V. SrinivasaRaghavan, “Lossless medical image compression algorithm using tetrolet transformation”, Journal of Ambient Intelligence and Humanized Computing, Feb. 2020
-
[7] S. Mallat, “Zero-Crossing of a Wavelet Transform”, IEEE Transactions on Information Theory, vol. 37 no. 4, pp. 1019-1033, Jul. 1991
-
[8] S. G. Mallat, “Multifrequency channel decompositions of images and wavelet models”, IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 37 no 12, pp. 2091-2110, Dec. 1989
-
[9] T. I. Saputra, Fauziah, N. Hayati, “Implementasi Discrete Wavelet Transform Pada Aplikasi Kompresi Citra Medis”, Jurnal Infomedia, vol. 4 no. 2, pp. 101-107, Dec. 2019.
-
[10] I. M. A. D. S. Atmaja, “Kompresi Citra Medis Menggunakan Packet Wavelet Transform dan Run Length Encoding”, Jurnal Matrix, vol. 8 no. pp 10-15, Mar. 2018
-
[11] I. D. G. H. Rastama, I. M. O. Widyantara, Linawati, “Teknik Kompresi Citra Medis dengan Transformasi Diskrit Wavelet dan Pengkodean
Entropy”, Jurnal Rekayasa Sistem dan Teknologi Informasi, vol. 4 no. 1, pp. 155-162, Feb. 2020
-
[12] F. A. Wara, A. J. Santoso, B. Y. Dwiandiyanta, “Pengaruh Derau (Noise) pada Pemampatan Intra-Frame Urutan Citra Gerak tari Hegong Menggunakan Alihragam Gelombang Singkat”, Seminar Nasional Sains dan Teknologi, Nov. 2016
-
[13] A. Dixit, S. Majumdar, “Comparative Analysis Of Coiflet And Daubechies Wavelets Using Global Threshold For Image De-Noising”, International Journal of Advances in Engineering & Technology, vol. 6 no 5, pp. 2247-2252, Nov. 2013
-
[14] E. G. T. Swee, S. Elangovan, “Applications of symlets for denoising and load forecasting”, Proceedings of the IEEE Signal Processing Workshop on Higher-Order Statistics, Jun. 1999
-
[15] R. C. Gonzalez, R. E. Woods, Digital Image Processingm (3rd Edition). New Jersey, United States: Prentice Hall. 2006
-
[16] G. Strang and T. Nguyen, Wavelets and Filter Banks. Cambridge Press, 1996
-
[17] F. Liu, M. H. Cabronero, V. Sanchez, M. W. Marcellin, A. Bilgin, “The Current Role of Image Compression Standards in Medical Imaging”, Information, vol. 8 no. 131, Oct. 2017
-
[18] C. S. Burrus, R. A. Gopinath, and H. Guo. Introduction to Wavelets and Wavelet Transforms, New Jersey, United State: Prentice Hall, 1998
-
[19] L. L. Winger, A. N. Venetsanopoulos, “Biorthogonal modified coiflet filters for image compression”, Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, May. 1998
-
[20] C. S. Burrus, I. E. Odegard, “Coiflet systems and zero moments”, IEEE Transactions on Signal Processing, vol. 46 no. 3, pp. 761-766, Mar. 1998
-
[21] K. Gopi, T.R. Shri, “Medical Image Compression Using Wavelet,” IOSR Journal of VLSI and Signal Processing (IOSR-JVSP), vol. 2 no. 4, pp 01-06, May-Jun. 2013
-
[22] I. Daubechies, “Orthonormal Bases of Compactly Supported Wavelet”, Communication on Pure and Applied Mathematics, vol. 41 no. 7, pp. 909-996, Oct. 1998
-
[23] A. Moffat. “Huffman Coding”, ACM Computing Surveys, vol. 1 no. 1, Jun. 2019
-
[24] D. A. Huffman, “A Method for the Construction of MinimumRedundancy Codes”, Proceedings of the IRE, vol. 40 no. 9, pp. 10981101, Sept. 1952
-
[25] I.H. Witten, R. M. Neal, J. G. Cleary, “Arithmetic Coding for Data Compression”, Communication of the ACM, vol. 30 no. 6, pp 520-540, Jun. 1987
-
[26] G. G. Langdon, “An Introduction to Arithmetic Coding”, IBM Journal of Research and Development, vol. 28 no. 2, pp. 135-149, Mar. 1984
-
[27] R.H. Sianipar, H.S. Mangiri, I.K. Wiryajati. MATLAB Untuk Pemrosesan Citra Digital. Bandung, Indonesia: INFORMATIKA Bandung. 2013
-
[28] I. M. O. Widyantara, I. G. A. G. D. Putri, N. P. Sastra, N. M. A. E. D. Wirastuti, “Selection of Mother Wavelet for Medical Image Compression”, International Conference Smart Green Technology in Electrical and Information System, pp 171-177, Okt. 2016
ISSN 1693 – 2951
I Gusti Ayu Garnita Darma Putri: Metode Kompresi Citra Medis…
Discussion and feedback