Analisis Metode Sistem Pendukung Keputusan Pemilihan Waktu Terbaik Perubahan Harga Dinamis Hotel

Majalah Ilmiah Teknologi Elektro, Vol. 18, No. 2, Mei - Agustus 2019

DOI: https://doi.org/10.24843/MITE.2019.v18i02.P02

155

Analisis Metode Sistem Pendukung Keputusan Pemilihan Waktu Terbaik Perubahan Harga Dinamis Hotel

I Wayan Surya Pramana¹, Rukmi Sari Hartati², Yoga Divayana³

[Submission: 04-10-2018, Accepted: 07-02-2019]

Abstract— Research discusses the decision support system method which is considered to be used for selection of the best time of hotel dynamic price change. The research was conducted by analyzing the results and process of applying the AHP, TOPSIS, SAW, and SMART methods in sample case of selection of the best time of hotel dynamic price change. The conclusions obtained from this research, the AHP and SAW methods have advantages in the consistency of the matrix and the calculation process compared to other methods. The writer recommends combining the AHP and SAW methods in decision support system of best time selection of hotel dynamic price change by considering matrix validity and ease of calculation process, with the hope that the decisions produced are more accurate with a less risk of errors.

Intisari— Penelitian membahas tentang metode dalam sistem pendukung keputusan yang dianggap dapat digunakan untuk pemilihan waktu terbaik perubahan harga dinamis hotel. Penelitian dilakukan dengan menganalisis hasil dan proses penerapan metode AHP, TOPSIS, SAW, dan SMART dalam contoh kasus pemilihan waktu perubahan harga dinamis di sebuah hotel. Kesimpulan yang diperoleh dari penelitian ini, metode AHP dan SAW memiliki kelebihan dalam konsistensi matriks dan proses perhitungan dibandingkan dengan metode lainnya. Penulis merekomendasikan penggabungan metode AHP dan metode SAW dalam sistem pendukung keputusan pemilihan waktu terbaik perubahan harga dinamis hotel dengan mempertimbangkan validitas matriks dan kemudahan proses perhitungan, dengan harapan bahwa keputusan yang dihasilkan lebih akurat dengan risiko kesalahan yang lebih kecil.

Kata Kunci— Harga Dinamis Hotel, Sistem Pendukung Keputusan, AHP, TOPSIS, SAW, SMART

• I.    pendahuluan

Menurut Bayoumi, dkk.[1], untuk dapat memaksimalkan pendapatan hotel, harga yang dinamis harus ditentukan dengan mempertimbangkan tingkat hunian hotel dan permintaan hunian saat ini dan masa depan. Hotel pada umumnya telah menetapkan variasi harga yang dapat dirubah secara dinamis sesuai dengan kondisi pasar, namun pemilihan waktu untuk perubahan harga tersebut masih ditentukan

secara manual, sehingga proses pemilihan sangat bergantung kepada keputusan user. Hal ini dapat berpengaruh pada pendapatan hotel, karena keputusan pemilihan waktu yang tidak tepat dapat menyebabkan penurunan pendapatan hotel.

Dalam jurnal [2] dan [3], suatu sistem pendukung keputusan diimplementasikan untuk membantu proses pengambilan keputusan dalam sebuah kasus pemilihan alternatif. Metode yang digunakan dalam sistem pendukung keputusan pada suatu kasus pemilihan alternatif dapat bervariasi, hal ini diketahui dari jurnal [4] yang menggunakan metode SMART dalam suatu sistem pendukung keputusan dalam pemilihan supplier, jurnal [5] yang menggunakan metode AHP dalam suatu sistem pendukung keputusan dalam pemilihan metode penyajian project, jurnal [6] yang menggunakan metode SAW dalam suatu sistem pendukung keputusan dalam pemilihan laptop dan jurnal [7] yang menggunakan metode TOPSIS dalam suatu sistem pendukung keputusan dalam pemilihan proses Rapid Prototyping (RP)

Berdasarkan hal tersebut, penelitian dilakukan dengan tujuan untuk menganalisis metode sistem pendukung keputusan yang dapat digunakan dalam suatu sistem pendukung keputusan untuk pemilihan waktu terbaik perubahan harga dinamis hotel. Penelitian ini dilakukan dengan menganalisis hasil dan proses penerapan empat metode sistem pendukung keputusan antara lain, metode Analytical Hierarchy Process (AHP), metode Simple Additive Weighting (SAW), metode Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) dan metode Simple Multi Attribute Rating Technique (SMART). Keempat metode ini dipilih berdasarkan dua hal antara lain belum terdapat penelitian yang melakukan analisis komparasi tentang mekanisme penerapan metode pendukung keputusan tersebut dan belum terdapat penelitian yang melakukan analisis terhadap keempat metode yang digunakan dalam penelitian ini secara bersamaan.

• II.    Metodologi

Lokasi, kerangka pelaksanaan, dan metode pengumpulan data yang digunakan dalam penelitian ini adalah sebagai berikut :

• A.    Lokasi penelitian

Penelitian berlokasi di Hotel Mercure Bali Nusa Dua

• B.    Kerangka pelaksanaan penelitian

Kerangka pelaksanaan penelitian adalah sebagai berikut :

p-ISSN:1693 – 2951; e-ISSN: 2503-2372

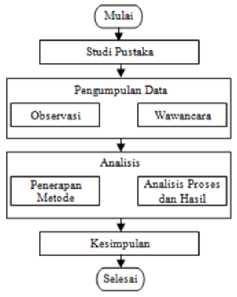
Gambar 1: Kerangka pelaksanaan penelitian

• C.    Metode pengumpulan data

Pengumpulan data yang digunakan dalam penelitian ini adalah sebagai berikut :

• •    Wawancara

Wawancara dilakukan kepada bapak Beni Kristyawan selaku Revenue and Reservation Manager Hotel Mercure Bali Nusa Dua

• •    Observasi

Observasi dilakukan pada proses perubahan harga dinamis

Hotel Mercure Bali Nusa Dua

• III.    Pembahasan dan analisis

Penerapan metode AHP, TOPSIS, SAW dan SMART dilakukan pada contoh kasus yang dibuat mengacu pada data actual di Hotel Mercure Bali Nusa Dua. Adapun parameter yang menjadi pertimbangan pengambilan keputusan pemilihan waktu perubahan harga dinamis berdasarkan hasil wawancara adalah sebagai berikut :

TABEL I

Parameter Perubahan Harga Dinamis

Parameter	Inisial
Competitor Rate	CT1
Average Room Rate	CT2
Occupancy	CT3
Public Pick Up Trend	CT4
Weekend Period	CT5
Event Period	CT6
Seasonality	CT7

Berdasarkan hasil observasi, diketahui beberapa hal sebagai berikut :

• •    Perubahan harga dinamis pasti dilakukan saat akhir minggu (hari jumat-hari minggu), saat ada event yang terjadi di kawasan Nusa Dua, Bali dan saat hari libur nasional

• •    Selama observasi dari tanggal 1 November 2018 hingga 30 November 2018, diketahui bahwa perubahan harga dinamis tidak dilakukan pada hari senin hingga kamis

Sehingga berdasarkan hal tersebut, parameter yang akan digunakan dalam pengujian metode adalah sebagai berikut :

TABEL II

Parameter Pengujian Metode

Parameter	Inisial
Competitor Rate	CT1
Average Room Rate	CT2
Occupancy	CT3
Public Pick Up Trend	CT4

Pembobotan parameter ditentukan berdasarkan skala yang diperoleh berdasarkan hasil wawancara, dengan rincian sebagai berikut :

TABEL III

Pembobotan Skala Parameter Perubahan Harga Dinamis

Parameter	Skala	Bobot
Competitor Rate	≥ Rp. 550.000	3
	Rp. 451.000 – Rp. 549.000	2
	< Rp. 450.000	1
Average Room Rate	≥ Rp. 550.000	3
	Rp. 451.000 – Rp. 549.000	2
	< Rp. 450.000	1
Occupancy	≥ 160 Kamar	3
	100 Kamar - 159 Kamar	2
	< 100 Kamar	1
Public Pick Up Trend	≥ 5 orang/hari	3
	1 orang/hari – 4 orang/hari	2
	0 orang/hari	1

Alternatif yang ditentukan untuk pengujian metode dalam penelitian berdasarkan perolehan data yaitu :

TABEL IV

Alternatif Keputusan Pemilihan Waktu Perubahan Harga Dinamis

Alternatif	Inisial
19 November 2018	ALT1
20 November 2018	ALT2
21 November 2018	ALT3
22 November 2018	ALT4

Alternatif tersebut ditentukan dengan pertimbangan bahwa pada tanggal 19 November 2018 hingga tanggal 22 November 2018 merupakan hari biasa tanpa event dan libur nasional, berdasarkan hasil observasi, dalam periode ini pada umumnya tidak dilakukan perubahan harga dinamis. Sehingga periode ini ditentukan sebagai alternatif keputusan untuk mengetahui waktu terbaik yang dapat dipilih untuk merubah harga dinamis Nilai parameter dari masing-masing alternatif dapat dilihat pada tabel 5 sebagai berikut :

TABEL V

Nilai Parameter Dari Setiap Alternatif Keputusan

Alt	Parameter
	CT1	CT2	CT3	CT4
Alt1	439551	483196	119	0
Alt2	446500	498876	85	0
Alt3	487500	496650	74	0
Alt4	482812	502815	91	0

DOI: https://doi.org/10.24843/MITE.2019.v18i02.P02

Parameter CT4 bernilai 0 karena pada tanggal 19 November 2018 hingga tanggal 22 November 2018 tidak ada public pick up(tamu individual)

• A) Metode Analytic Hierarchy Process (AHP)

Pada tahun 1970an, Thomas L. Saaty memperkenalkan sebuah metode pendukung keputusan yang disebut dengan metode Analytic Hierarchy Process (AHP) [8]. AHP merupakan sebuah metode untuk membantu proses pengambilan keputusan yang merepresentasikan kriteria dan alternatif keputusan kedalam bentuk hierarki [9]. Dengan pembentukan hierarki ini, setiap masalah akan terlihat lebih terstruktur dan sistematis.

Fokus utama dalam metode AHP, antara lain [10]:

• •    Data yang digunakan dalam metode ini merupakan data yang diperoleh berdasarkan kriteria yang dipertimbangkan dalam pengambilan keputusan.

• •    Pemberian nilai untuk setiap kriteria yang digunakan dalam metode ini harus ditentukan oleh pengambil keputusan.

Penerapan metode AHP dalam pemilihan waktu terbaik perubahan harga dinamis pada contoh kasus adalah sebagai berikut :

• 1)    Penentuan tujuan : Untuk pemilihan waktu terbaik perubahan harga dinamis hotel

• 2)    Pembuatan struktur hirarki : Struktur hirarki metode AHP dalam kasus pemilihan waktu perubahan harga dinamis hotel ditunjukkan pada gambar 2

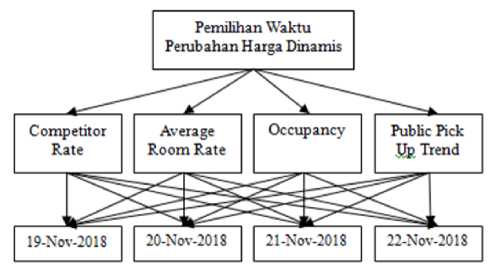
Gambar 2. Struktur hierarki untuk pemilihan waktu perubahan harga dinamis metode AHP

• 3)    Penyusunan pairwise comparison matrix : Matriks disusun berdasarkan intensitas kepentingan. Intensitas kepentingan merupakan nilai perbandingan antara seluruh kriteria yang digunakan dalam proses pengambilan keputusan [11].

TABEL VI

Nilai Intensitas Kepentingan Dalam Metode AHP

Skala Kepentingan	Keterangan
1	Kedua Kriteria Sama Penting

I.W.S. Pramana: Analisis Metode Sistem pendukung …

3	Salah Satu Kriteria Sedikit Lebih Penting
5	Salah Satu Kriteria Lebih Penting
7	Salah Satu Kriteria Sangat Lebih Penting
9	Salah Satu Kriteria Mutlak Lebih Penting
Kebalikan	Nilai Invers Dari Skala Kepentingan

Intensitas kepentingan antara parameter dalam pemilihan waktu terbaik perubahan harga dinamis berdasarkan hasil wawancara adalah sebagai berikut :

• •    Average Room Rate lebih penting daripada Competitor Rate

• •    Occupancy sedikit lebih penting daripada Competitor Rate

• •    Public Pick Up Trend lebih penting daripada Average Room Rate, Occupancy dan Competitor Rate

• •    Average Room Rate sama pentingnya dengan Occupancy

Sehingga diperoleh matriks berdasarkan intensitas kepentingan tersebut sebagai berikut :

TABEL VII

Matriks Pairwise comparison

	CT1	CT2	CT3	CT4
CT1	1	1/5	1/3	1/5
CT2	5	1	1	1/5
CT3	3	1	1	1/5
CT4	5	5	5	1

• 4)    Normalisasi dan pengecekan konsistensi matriks: Proses normalisasi dan pengecekan matriks adalah sebagai berikut :

TABEL VIII

Matriks Pairwise comparison Desimal

	CT1	CT2	CT3	CT4
CT1	1	0.2	0.333	0.2
CT2	5	1	1	0.2
CT3	3	1	1	0.2
CT4	5	5	5	1
Total	14	7.2	7.333	1.6

Nilai normalisasi dihitung dengan cara sebagai berikut : 1

(C1,C1) = —= 0.071, dst..

Sehingga diperoleh hasil sebagai berikut :

TABEL IX

Matriks Pairwise comparison Ternormalisasi

	CT1	CT2	CT3	CT4
CT1	0.071	0.028	0.045	0.125
CT2	0.357	0.139	0.136	0.125
CT3	0.214	0.139	0.136	0.125
CT4	0.357	0.694	0.682	0.625

Pengecekan konsistensi dilakukan dengan tahapan sebagai berikut :

p-ISSN:1693 – 2951; e-ISSN: 2503-2372

A) Menghitung criteria weight (W): Criteria weight dapat dihitung dengan cara sebagai berikut :

...       0.071 + 0.028 + 0.045 + 0.125

^w(ci) =----------4----------

W(C₁) = ⁰2⁷⁰ = 0.067, dst..

E) Menghitung Consistency Ratio : Consistency Ratio dihitung dengan menggunakan persamaan 3 [13]:

CI

^cr= «7

(3)

Sehingga diperoleh hasil sebagai berikut :

TABEL X

Criteria Weight

Dimana :

CR= Consistency ratio

CI = Consistency index

RI = Random index

	W
CT1	0.067
CT2	0.189
CT3	0.154
CT4	0.590

Pada metode AHP, nilai random index ditentukan seperti dalam tabel 12 :

TABEL XII

Random Index

B) Menghitung weight sum vector (Ws) : Weight sum vector dapat dihitung dengan cara sebagai berikut :

N	1	2	3	4	5	6	7	8
RI	0	0	0.58	0.9	1.12	1.24	1.32	1.41

Perhitungan dilakukan dengan cara sebagai berikut :

0.090

0.9

CR =

= 0.1

(1 * 0.067) + (0.2 * 0.189) + (0.333 * 0.154) + (0.2 * 0.590)

W =------------------------------- ^s                             0.067

W_s = 4.071, dst...

Sehingga diperoleh hasil sebagai berikut :

TABEL XI

Weight Sum Vector

Karena consistency ratio (CR) ≤ 0.1, maka pairwise comparison matrix dinyatakan konsisten

• 5)    Pengulangan langkah 3 dan 4 untuk semua alternatif keputusan

• A) Competitor Rate (CT1)

	Ws
CT1	4.071
CT2	4.214
CT3	4.316
CT4	4.480

TABEL XIII

Matriks Pairwise Comparison Alternatif Terhadap CT1

	ALT1	ALT2	ALT3	ALT4
ALT1	1	1	1/3	1/3
ALT2	1	1	1/3	1/3
ALT3	3	3	1	1
ALT4	3	3	1	1

C) Menghitung max : Rumus untuk menghitung Λ max dapat dilihat pada persamaan 1 [12] :

TABEL XIV

Criteria Weight Alternatif Terhadap CT1

1     ∑Ws

Imax =--- n

(1)

Dimana :

λ Max = Eigen Value

∑W_s = Total weight sum vector

n = Number of criteria

	Criteria Weight
ALT1	0.125
ALT2	0.125
ALT3	0.375
ALT4	0.375

Perhitungan dilakukan dengan cara sebagai berikut :

((4.071) + (4.214) + (4.316) + (4.480))

A max =----------------------------

4

A max = ^17.082 = 4.270

4

B) Average Room Rate (CT2)

TABEL XV

Matriks Pairwise Comparison Alternatif Terhadap CT2

D) Menghitung Consistency Index : Consistency Index diperoleh menggunakan persamaan 2 [13]:

	ALT1	ALT2	ALT3	ALT4
ALT1	1	1	1	1
ALT2	1	1	1	1
ALT3	1	1	1	1
ALT4	1	1	1	1

CI =

Amax — n

n-1

(2)

TABEL XVI

Criteria Weight Alternatif Terhadap CT2

Dimana :

λ Max = Eigen Value

CI = Consistency index n = Number of criteria

Perhitungan dilakukan dengan cara sebagai berikut :

	Criteria Weight
ALT1	0.250
ALT2	0.250
ALT3	0.250
ALT4	0.250

_ci   (4.270) — 4

4 — 1

0.090

Majalah Ilmiah Teknologi Elektro, Vol. 18, No. 2, Mei - Agustus 2019

DOI: https://doi.org/10.24843/MITE.2019.v18i02.P02                                                              159

Dengan metode AHP, diperoleh hasil waktu terbaik untuk merubah harga dinamis pada contoh kasus adalah pada alternatif ke-1 (Tanggal 19 November 2018)

• C) Occupancy (CT3)

  TABEL XVII

  Matriks Pairwise Comparison Alternatif Terhadap CT3

  
  

  	ALT1	ALT2	ALT3	ALT4
  ALT1	1	3	5	3
  ALT2	1/3	1	3	1
  ALT3	1/5	1/3	1	1/3
  ALT4	1/3	1	3	1

  
  

  TABEL XVIII

  Criteria Weight Alternatif Terhadap CT3

  
  

  	Criteria Weight
  ALT1	0.519
  ALT2	0.201
  ALT3	0.079
  ALT4	0.201

  
  

  D) Public Pick Up Trend (CT4)

  TABEL XIX

  Matriks Pairwise Comparison Alternatif Terhadap CT4

  
  

  • B.    Metode Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)

  Dalam metode TOPSIS, alternatif keputusan terbaik adalah alternatif keputusan yang memiliki nilai solusi ideal positif yang paling kecil dan nilai solusi ideal negatif yang paling besar [14][15].

  Penerapan metode TOPSIS dalam pemilihan waktu terbaik perubahan harga dinamis pada contoh kasus adalah sebagai berikut :

  • 1)    Menentukan parameter dan alternatif keputusan: Data yang digunakan dalam penerapan metode ini dapat dilihat pada tabel 2 dan tabel 4

  • 2)    Penentuan atribut dan nilai bobot parameter serta penentuan nilai untuk setiap skala parameter : Atribut dan bobot nilai setiap parameter ditentukan sebagai berikut:

  TABEL XXII

  Atribut Dan Pembobotan Parameter

  
  

  	ALT1	ALT2	ALT3	ALT4
  ALT1	1	1	1	1
  ALT2	1	1	1	1
  ALT3	1	1	1	1
  ALT4	1	1	1	1

  
  

  Parameter	Inisial	Bobot	Atribut
  Competitor Rate	CT1	10%	Benefit
  Average Room Rate	CT2	25%	Benefit
  Occupancy	CT3	25%	Benefit
  Public Pick Up Trend	CT4	40%	Benefit

  
  

TABEL XX

Criteria Weight Alternatif Terhadap CT4

	Criteria Weight
ALT1	0.250
ALT2	0.250
ALT3	0.250
ALT4	0.250

• 6)    Perhitungan nilai akhir dan perangkingan alternatif: Nilai akhir pemilihan waktu terbaik perubahan harga dinamis hotel menggunakan metode AHP adalah sebagai berikut :

TABEL XXI

Nilai Akhir Dan Rangking Alternatif Metode AHP

Criteria Weight	CT1	CT2	CT3	CT4
	0.067	0.189	0.154	0.590
ALT1	0.125	0.250	0.519	0.250
ALT2	0.125	0.250	0.201	0.250
ALT3	0.375	0.250	0.079	0.250
ALT4	0.375	0.250	0.201	0.250

Criteria Weight	Nilai Akhir	Rangking
ALT1	0.283	1
ALT2	0.234	3
ALT3	0.232	4
ALT4	0.251	2

• 3)    Penyusunan matriks dan normalisasi: Nilai alternatif pada tabel 5 dikonversi ke nilai yang telah ditentukan pada tabel 3 sebagai berikut :

TABEL XXIII

Matriks Bobot Alternatif

	CT1	CT2	CT3	CT4
ALT1	1	2	2	1
ALT2	1	2	1	1
ALT3	2	2	1	1
ALT4	2	2	1	1

Normalisasi matriks diperoleh menggunakan persamaan berikut [6]:

R_tJ = X_tJ

O)

-1/2

(4)

Perhitungan dilakukan dengan cara sebagai berikut :

R₁₁ = 1 * (1² + 1² + 2² + 2²)^-1/² = 0.316, _dst _

Sehingga diperoleh hasil sebagai berikut :

TABEL XXIV

Matriks Bobot Alternatif Ternormalisasi

I.W.S. Pramana: Analisis Metode Sistem pendukung …

p-ISSN:1693 – 2951; e-ISSN: 2503-2372

	CT1	CT2	CT3	CT4
ALT1	0.316	0.500	0.756	0.500
ALT2	0.316	0.500	0.378	0.500
ALT3	0.632	0.500	0.378	0.500
ALT4	0.632	0.500	0.378	0.500

4) Perhitungan weighted normalized matrix : Weighted normalized matrix diperoleh dengan persamaan 5 [6]:

V_ij =X_ij *Wj

(5)

7) Perhitungan nilai akhir dan perangkingan alternatif keputusan: Nilai akhir diperoleh dengan menggunakan rumus sebagai berikut [6]:

P1

Si-

Si⁺ +Si-

(7)

Perhitungan dilakukan dengan cara sebagai berikut :

V₁₁ = 0.316 * 0.1 = 0.032, dst

Sehingga diperoleh hasil sebagai berikut :

TABEL XXV

Weighted Normalized Matrix Bobot Alternatif

	CT1	CT2	CT3	CT4
ALT1	0.032	0.125	0.189	0.200
ALT2	0.032	0.125	0.094	0.200
ALT3	0.063	0.125	0.094	0.200
ALT4	0.063	0.125	0.094	0.200

• 5)    Menghitung solusi ideal positif dan solusi ideal negatif: Dikarenakan seluruh parameter yang digunakan mempunyai atribut benefit, maka perhitungan dilakukan dengan cara :

• V₁⁺ = Max (0.032; 0.032; 0.063; 0.063) = 0.063, dst...

• V₁^- = Min (0.032; 0.032; 0.063; 0.063) = 0.032, dst

Sehingga diperoleh hasil sebagai berikut :

TABEL XXVI

Positif Ideal Solution dan Negative Ideal Solution

	CT1	CT2	CT3	CT4
V+	0.063	0.125	0.189	0.200
V-	0.032	0.125	0.094	0.200

• 6)    Perhitungan jarak Euclidean : Perhitungan dilakukan berdasarkan solusi ideal positif dan solusi ideal negatif dengan menggunakan rumus sebagai berikut [6]:

  ^S;' (∑^{iv v}'¹j

  
  

  (6)

  
  

Perhitungan dilakukan dengan cara sebagai berikut :

_s∙₊ _ /(0.032 - 0.063)² + (0.125 - 0.125)² + (0.189 - 0.189)²∖^as

ⁱ = V                  +(0.200 - 0.200)^{2                  J}

Si⁺ = 0.032, dst.

Dan,

_s∙- _ /(0.032 - 0.032)² + (0.125 - 0.125)² + (0.189 - 0.094)²∖^a5

ⁱ =V                 +(0.200 - 0.200)²                 J

Sr = 0.094, dst.

Perhitungan dilakukan dengan cara sebagai berikut :

P1

0.094

0.094 + 0.032

0.749, dst .

Sehingga diperoleh hasil akhir sebagai berikut:

TABEL XXVIII

Nilai Akhir dan Rangking Alternatif Metode TOPSIS

	Nilai Akhir	Ranking
ALT1	0.749	1
ALT2	0.000	3
ALT3	0.251	2
ALT4	0.251	2

Dengan metode TOPSIS, diperoleh hasil waktu terbaik untuk merubah harga dinamis pada contoh kasus adalah pada alternatif ke-1 (Tanggal 19 November 2018)

• C. Metode Simple Additive Weigthing (SAW)

Salah satu metode dalam Multi Attribute Decision Making (MADM) yaitu Simple Additive Weighting atau lebih dikenal dengan nama metode SAW [16] memiliki pemahaman bahwa alternatif keputusan terbaik dapat diperoleh berdasarkan bobot dari alternatif keputusan untuk setiap kriteria yang digunakan dalam proses pengambilan keputusan [17][25]. Metode SAW membutuhkan proses normalisasi matriks berdasarkan jenis setiap kriteria untuk semua alternatif keputusan, dan mengharuskan pengambil keputusan untuk menentukan bobot untuk setiap kriteria [18]. Metode SAW memiliki waktu perhitungan yang singkat, sehingga metode ini dianggap efisien untuk proses pengambilan keputusan [19]

Penerapan metode SAW dalam pemilihan waktu terbaik perubahan harga dinamis pada contoh kasus adalah sebagai berikut :

• 1)    Penentuan parameter, tipe dan bobot parameter : Parameter yang digunakan dalam penerapan metode SAW dapat dilihat pada tabel 2, tipe dan bobot dari masing-masing parameter ditentukan sebagai berikut :

TABEL XXIX

Tipe Dan Pembobotan Parameter

Sehingga diperoleh hasil sebagai berikut

TABEL XXVII

Jarak Euclidean Dari Positif Ideal Solution dan Negative Ideal Solution

	Si+	Si-
ALT1	0.032	0.094
ALT2	0.100	0.000
ALT3	0.094	0.032
ALT4	0.094	0.032

Parameter	Inisial	Bobot	Tipe
Competitor Rate	CT1	10%	Benefit
Average Room Rate	CT2	25%	Benefit
Occupancy	CT3	25%	Benefit
Public Pick Up Trend	CT4	40%	Benefit

• 2)    Penyusunan matriks X : Matriks X disusun dari nilai alternatif pada tabel 5 yang dikonversi ke nilai yang telah ditentukan pada tabel 3 sebagai berikut :

TABEL XXX

Matriks Bobot Alternatif

	CT1	CT2	CT3	CT4
ALT1	1	2	2	1
ALT2	1	2	1	1
ALT3	2	2	1	1
ALT4	2	2	1	1

ALT3	1	1	0.5	1
ALT4	1	1	0.5	1

Sehingga diperoleh matriks X sebagai berikut :

r 12 2

112 1

) 2 2 1

221

1

1

1

1

I

	Nilai Akhir	Ranking
ALT1	0.95	1
ALT2	0.825	3
ALT3	0.875	2
ALT4	0.875	2

3) Normalisasi matriks X ke matriks R : Nilai normalisasi matriks X ke matriks R dapat dihitung dengan menggunakan rumus sebagai berikut [20] :

R_ij = Max . 'Jik^a kriteria bertipe benefit     (8)

Min(χ..y

R_ij =----— ,Jika kriteria bertipe cost      (9)

Dimana :

X_ij = Elemen matriks X

Rij = Nilai normalisasi matriks X

Dengan menggunakan metode Simple Additive Weighting (SAW), diperoleh hasil waktu terbaik untuk merubah harga dinamis pada contoh kasus adalah pada alternatif ke-1 (Tanggal 19 November 2018)

Dalam kasus ini semua parameter memiliki tipe yang sama yaitu tipe benefit, maka nilai normalisasi dihitung dengan cara sebagai berikut :

R

1.1

1

Max {1;1;2;2}

¹ = 0.5 , dst.. 2            ^,

Sehingga diperoleh matriks R sebagai berikut :

r0.5  11

10.5  10.5

1   10.5

1   10.5

1

1

1

1

I

4) Perhitungan nilai akhir dan perangkingan alternatif : Nilai akhir dapat dihitung dengan menggunakan rumus sebagai berikut [20]:

D. Metode Simple Multi Attribute Rating Technique (SMART)

Pada tahun 1977, Edward mengembangkan metode pengambilan keputusan multi kriteria yang dikenal dengan metode SMART [21]. Dalam pemahaman metode SMART setiap alternatif memiliki kriteria dengan nilai dan setiap kriteria memiliki bobot yang menunjukkan pengaruh masing-masing kriteria satu dan yang lainnya [22]. Ketika menilai utility keseluruhan, metode SMART memiliki keuntungan dengan menambahkan penekanan pada atribut yang lebih penting sambil mengurangi nilai atribut yang lebih rendah [23]

Penerapan metode SMART dalam pemilihan waktu terbaik perubahan harga dinamis hotel adalah sebagai berikut :

1) Penentuan parameter dan bobot parameter : Parameter yang digunakan dalam penerapan metode SMART dapat dilihat pada tabel 2 dan bobot dari setiap parameter adalah sebagai berikut :

TABEL XXXII

Parameter Dan Bobot Parameter

Vi_j =^ W_jRi_j                  (10)

i=1

Dimana :

Vij = Nilai Akhir

Wj = Nilai Kriteria

Rij = Nilai Normalisasi Matriks X

Perhitungan dilakukan dengan cara sebagai berikut :

V₁ = (0.10 * 0.5) + (0.25 * 1) + (0.25 * 1) + (0.40 * 1)

V₁ = 0.95, dst..

Sehingga diperoleh hasil sebagai berikut :

TABEL XXXI

Nilai Akhir dan Rangking Alternatif Metode SAW

	CT1	CT2	CT3	CT4
Bobot	0.10	0.25	0.25	0.40
ALT1	0.5	1	1	1
ALT2	0.5	1	0.5	1

Parameter	Inisial	Bobot
Competitor Rate	CT1	10
Average Room Rate	CT2	25
Occupancy	CT3	25
Public Pick Up Trend	CT4	40

• 2)    Normalisasi parameter : Normalisasi bobot parameter dapat dihitung dengan cara sebagai berikut :

  C1 =

  
  

  10

  100 = ^0.1,

  
  

  dst..

  
  

Sehingga diperoleh hasil sebagai berikut :

TABEL XXXIII

Bobot Ternormalisasi

I.W.S. Pramana: Analisis Metode Sistem pendukung …

p-ISSN:1693 – 2951; e-ISSN: 2503-2372

Parameter	Bobot	Normalisasi
Competitor Rate	10	0.10
Average Room Rate	25	0.25
Occupancy	25	0.25
Public Pick Up Trend	40	0.40
Total	100

• 3)    Perhitungan nilai utility : Nilai utility dapat dihitung dengan menggunakan rumus sebagai berikut [24]:

Dengan metode SMART, diperoleh hasil waktu terbaik untuk merubah harga dinamis pada contoh kasus adalah pada alternatif ke-1 (Tanggal 19 November 2018)

^uij(^aij)-

^Uout  ^Umin

^Umax  ^Umin

(11)

Dimana :

Uij(Aij) = Nilai utility

Cout = Nilai element matriks

Cmin = Nilai minimum dari skala dalam kriteria yang dinilai

Cmax = Nilai maksimum dari skala dalam kriteria yang dinilai

Nilai utility dihitung berdasarkan nilai alternatif pada tabel 7 yang dikonversi ke nilai yang telah ditentukan pada tabel 36 sebagai berikut :

TABEL XXXIV

Matriks Bobot Alternatif

	CT1	CT2	CT3	CT4
ALT1	1	2	2	1
ALT2	1	2	1	1
ALT3	2	2	1	1
ALT4	2	2	1	1

Nilai utility dihitung dengan cara sebagai berikut :

4 — 1

^(XJ- —- - 0.75, dst..

Sehingga diperoleh hasil sebagai berikut :

TABEL XXXV

Nilai Utility

	CT1	CT2	CT3	CT4
ALT1	0	0.25	0.25	0
ALT2	0	0.25	0	0
ALT3	0.25	0.25	0	0
ALT4	0.25	0.25	0	0

• 4)    Perhitungan nilai akhir dan perangkingan alternatif :

Nilai akhir dihitung dengan cara sebagai berikut :

ALT1 - (0,1 * 0) + (0.25 * 0.25) + (0.25 * 0.25) + (0.40 * 0)

ALT1 - 0,125, dst..

Sehingga diperoleh hasil sebagai berikut :

TABEL XXXVI

Nilai Akhir dan Rangking Alternatif Metode SMART

	CT1	CT2	CT3	CT4
	0.1	0.25	0.25	0.4
ALT1	0	0.25	0.25	0
ALT2	0	0.25	0	0
ALT3	0.25	0.25	0	0
ALT4	0.25	0.25	0	0

• E. Analisis Hasil

Berdasarkan hasil penerapan empat metode diatas pada contoh kasus pemilihan waktu terbaik perubahan harga dinamis hotel, diperoleh hasil analisis sebagai berikut :

• •    Analisis proses pembobotan

Dari hasil penerapan keempat metode diatas, proses pembobotan mempunyai peran paling penting dari keseluruhan proses. Dalam penelitian diketahui bahwa perbedaan narasumber dalam proses pembobotan menyebabkan hasil akhir dari keluruhan proses menjadi berbeda

• •    Analisis proses perhitungan

Dalam proses perhitungan, metode SAW mempunyai kelebihan dari metode yang lain karena pada metode SAW menggunakan proses perhitungan yang sederhana, sehingga mengurangi resiko kesalahan dalam perhitungan

• •    Analisis proses penerapan

Dalam penerapan metode, metode AHP mempunyai kelebihan dari metode yang lain, yaitu konsistensi matriks. Dalam AHP terdapat tahapan pengecekan konsistensi yaitu memeriksa validitas matriks yang disusun berdasarkan pembobotan kriteria. Hanya matriks yang dinilai konsisten yang dapat digunakan dalam proses selanjutnya.

Berdasarkan hasil analisis diatas, metode AHP dan SAW diuji untuk diterapkan secara bersamaan dalam satu proses perhitungan untuk mengetahui kemungkinan penggabungan kedua metode tersebut dalam contoh kasus pemilihan waktu terbaik perubahan harga dinamis hotel dengan rincian sebagai berikut :

• 1)    Pembobotan kriteria : Bobot kriteria menggunakan bobot yang ditentukan dalam penerapan metode AHP pada tabel 11

• 2)    Perhitungan nilai akhir : Nilai akhir diperoleh dengan menjumlahkan hasil perkalian antara elemen matriks R yang merupakan normalisasi dari matriks X pada tabel 29 dengan bobot kriteria yang ditentukan dalam penerapan metode AHP pada tabel 10 dengan cara sebagai berikut :

V₁ - (0.067 * 0.5) + (0.189 * 1) + (0.154 * 1) + (0.590 * 1)

• V₁    - 0.967, dst..

Sehingga diperoleh hasil sebagai berikut :

TABEL XXXVII

Nilai Akhir dan Rangking Alternatif Metode AHP - SAW

	Nilai Akhir	Rangking
ALT1	0.125	1
ALT2	0.063	3
ALT3	0.088	2
ALT4	0.088	2

	CT1	CT2	CT3	CT4
Criteria Weight	0.067	0.189	0.154	0.590
ALT1	0.500	1.000	1.000	1.000
ALT2	0.500	1.000	0.500	1.000
ALT3	1.000	1.000	0.500	1.000
ALT4	1.000	1.000	0.500	1.000

	Nilai Akhir	Rangking
ALT1	0.967	1
ALT2	0.890	3
ALT3	0.923	2
ALT4	0.923	2

Penggunaan metode AHP dan SAW secara bersamaan pada satu proses memperoleh hasil waktu terbaik perubahan harga dinamis hotel yang sama dengan penggunaan metode tersebut secara terpisah yaitu pada alternatif ke-1 (Tanggal 19 November 2018)

• IV. Kesimpulan

Berdasarkan analisis terhadap penerapan metode AHP, TOPSIS, SAW dan SMART dalam pemilihan waktu terbaik perubahan harga dinamis hotel dengan menggunakan contoh kasus berdasarkan data actual di Hotel Mercure Bali Nusa Dua, diperoleh kesimpulan sebagai berikut :

• 1.    Metode Analytic Hierarchy Process (AHP) memiliki kelebihan yaitu dalam konsistensi matriks, yang mana tidak dimiliki oleh metode lain. Konsistensi matriks berguna untuk memeriksa validitas matriks yang disusun berdasarkan pembobotan kriteria

• 2.    Metode Simple Additive Weighting (SAW) memiliki proses perhitungan yang paling sederhana jika dibandingkan dengan ketiga metode lainnya. Hal ini dapat mengurangi resiko kesalahan dalam proses perhitungan Sehingga berdasarkan hasil penelitian, direkomendasikan

penggabungan metode AHP dan metode SAW dalam sistem pendukung keputusan pemilihan waktu terbaik perubahan harga dinamis hotel dengan pertimbangan validitas matriks dan kemudahan proses perhitungan, sehingga diharapkan keputusan yang dihasilkan lebih akurat dengan resiko kesalahan lebih kecil

Ucapan Terimakasih

Terimakasih untuk Hotel Mercure Bali Nusa Dua yang telah menyediakan tempat penelitian dan terimakasih untuk Bapak Beni Kristyawan selaku Revenue and Reservation Manager Hotel Mercure Bali Nusa Dua atas saran, pandangan, pengalaman dan bantuan yang diberikan selama penelitian.

Referensi

• [1]    Bayoumi, A., E., et al. “Dynamic pricing for hotel revenue management using price multipliers”. Journal of Revenue and Pricing Management Vol. 12, No.3, Pp. 271–285. 2013

• [2]    Ghodyspour S.H. dan O’Brien C. “A Decision Support System for Supplier Selection Using an Integrated Analytic Hierarchy Process and Linier Programming”. Int. J. Production Economics 56-57. Pp. 199212. 1998

• [3]    Cebeci U. “Fuzzy AHP-based Decision Support System for Selecting ERP System in Textile Industry by Using Balanced Scorecard”. Expert System with Applications 36. Pp 8900-8909. 2009

• [4]    Chou S.Y. dan Chang Y.H. “A Decision Support System for Supplier Selection Based on a Strategy-Aligned Fuzzy SMART Approach”. Expert System with Applications 34. Pp 2241-2253. 2008

• [5]    Mahdi I.M dan Alreshaid K. “Decision Support System for Selecting the Proper Project Delivery Method Using Analytical Hierarchy

I.W.S. Pramana: Analisis Metode Sistem pendukung …

Process (AHP)”. International Journal of Project Management 23. Pp 564–572. 2005

Khairul, Simaremare M. dan Siahaan A.P.U “. Decision Support System in Selecting The Appropriate Laptop Using Simple Additive Weighting”. International Journal of Recent Trends in Engineering & Research (IJRTER). 2016

Byun H.S dan Lee K.H. “A Decision Support System For The Selection of a Rapid Prototyping Process Using the Modified TOPSIS Method”. Int. J. Adv. Manuf Technol 26. Pp 1338–1347. 2005

Natasya, W.A.G dan Kusnawi K.,” Decision Support System Design to Decide on the Latest Smartphone Using Analytical Hierarchy Process”. 2nd International Conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE). 2017

Satriani N.N, Cholissodin I., dan Fauzi M.A. “Sistem Pendukung Keputusan Penentuan Calon Penerima Beasiswa BBP-PPA Menggunakan Metode AHP-PROMETHEE I Studi Kasus : FILKOM Universitas Brawijaya”. Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer. Vol.2, No.7. Pp. 2780-2788. 2018

Pujadi T., Fathurrozi A.,Teresia S. “Using Analytical Hierarchy Process for the Decission Support System in Teacher Placement”. International Conference on Information Management and Technology (ICIMTech). Pp. 182.187. 2016

Rahadian R., Hidayat N., dan Dewi R.K. “Sistem Pendukung Keputusan Penentuan Penerima Bantuan Keluarga Miskin Menggunakan Metode Analytical Hierarchy Process – Preference Ranking Organization for Enrichment Evaluation II (AHP-PROMETHEE II)”. Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer. Vol.2, No.5. Pp 1980-1985. 2018

Gustinar, Sarjono. “Analisis Dan Perancangan Sistem Pendukung Keputusan Pemilihan Guru Berprestasi Dengan Metode AHP (Analytic Hierarchy Proces ) Pada Smkn 9 Muaro Jambi”. Jurnal Manajemen Sistem Informasi. Vol. 3, No.1. Pp 922-935. 2018

Sari F.R., dan Sensuse D.I. “Penerapan Metode Analytic Hierarchy Process Dalam Sistem Penunjang Keputusan Untuk Pemilihan Asuransi”. Jurnal Sistem Informasi MTI-UI. Vol.4, No.2.2018

Chen SJ dan Hwang CL “Fuzzy multiple attribute decision-making – methods and application”. Springer Berlin Heidelberg, New York. 1992

Yoon KP dan Hwang CL (1995) Multiple attribute decision-making: an Introduction. Sage university paper series on quantitative applications in the social science, 07-104. 1995

Pranolo A.,dan Widyastuti S.,M.” Simple Additive Weighting Method on Intelligent Agent for Urban Forest Health Monitoring”. International Conference on Computer, Control, Informatics and Its Applications. Pp. 132-135. 2014

Ismanto E., dan Effendi N. “Sistem Pendukung Keputusan Penerimaan Karyawan Dengan Metode Simple Additive Weighting (SAW)”. SATIN - Saints dan Teknologi Informasi, Vol. 03, No. 01, 2017

Sarmadi, dan Effiyaldi. “Analisis Dan Perancangan Sistem Pendukung Keputusan Pemilihan Kendaraan Roda Dua Menggunakan Metode Simple Additive Weighting (SAW)(Studi Kasus : Pt. Sinar Sentosa)”. Jurnal Manajemen Sitem Informasi. Vol.3, No.1, Pp. 911-921. 2018 Daniati E., dan Nugroho A.” K-Means Clustering With Decision Support System using SAW”. 6th IEEE International Conference on Control System, Computing and Engineering. Pp. 326-331. 2016

Salim M.A.”Sistem Pendukung Keputusan Pemilihan Penerima Bantuan Perbaikan Rumah Menggunakan Metode Simple Additive Wieghting (SAW) Studi Kasus Kelurahan Tambelan Sampit Kota Pontianak”. Jurnal SISTEMASI, Vol. 7, No. 2, Pp. 120 – 131. 2018 Putri F.E.,Rahmansyah M.,dan Ariandi V. “Perancangan Sistem Pendukung Keputusan Untuk Menyeleksi Siswa Magang Ke Jepang Menggunakan Metode Simple Multi Attribute Rating Technique (SMART) Berbasis Web” (Studi Kasus : Lpk Hinomaru Padang)”. Majalah Ilmiah, Vol. 25, No. 1, Pp. 24-36. 2018

Astuti P.W. “Sistem Pendukung Keputusan Pemilihan Kegiatan Ekstrakurikuler Dengan Metode Smart Pada MAS PAB 1 Sampali”. Pelita Informatika Budi Darma, Vol. Ix, No.2, 2015

Taylor J.,M., dan Love B.,N.” Simple multi-attribute rating technique for renewable energy deployment decisions (SMART REDD)”. Journal p-ISSN:1693 – 2951; e-ISSN: 2503-2372

of Defense Modeling and Simulation: Applications, Methodology, Technology. Vol.11, No.3. Pp. 227-232. 2014

• [24]    Magrisa T., Wardhani K.D.K., dan Saf M.R.A. “Implementasi Metode SMART Pada Sistem Pendukung Keputusan Pemilihan Kegiatan Ekstrakurikuler Untuk Siswa Sma” Informatika Mulawarman: Jurnal Ilmiah Ilmu Komputer. Vol. 13, No. 1. Pp 49-55. 2018

• [25]    Fermanta, M.A, Suyadnya, I. M. A., dan Wirastuti, N.M.A.E.D. “Rancang Bangun Sistem Pendukung Keputusan Seleksi Tenaga Kerja Berbasis Web Menggunakan Metode Simple Additive Weighting Pada Pt. Solusi Lintas Data Cabang Bali”. Teknologi Elektro, Vol. 15, No. 2, 2016

ISSN 1693 – 2951

I.W.S. Pramana: Analisis Metode Sistem pendukung …