PENGGUNAAN METODE URUTAN (SEQUENCE METHOD) PADA ANALISIS HARMONISA UNTUK SISTEM KELISTRIKAN TAK-SEIMBANG
on
Penggunaan Metode Urutan . . .
I Wayan Rinas
PENGGUNAAN METODE URUTAN (SEQUENCE METHOD) PADA ANALISIS HARMONISA UNTUK SISTEM KELISTRIKAN TAK-SEIMBANG
I Wayan Rinas
Staf Pengajar Teknik Elektro Fak. Teknik Universitas Udayana, Kampus Bukut Jimbaran Bali.
Intisari
Peningkatan beban-beban nonlinier yang terpasang pada sistem akan menyebabkan terjadinya distorsi harmonisa. Distorsi harmonisa pada bentuk gelombang tegangan dan arus dapat mengakibatkan kondisi tidak normal pada sistem.
Pada sistem 3 phasa nonlinier, distorsi harmonisa akan menyebakan kondisi takseimbang. Tegangan
takseimbang dapat memunculkan komponen urutan negatif dan urutan nol yang merugikan sistem. Komponen urutan negatif akan mengakibatkan peningkatan panas yang berlebihan, sedangkan komponen urutan nol disamping dapat menyebabkan peningkatan rugi-rugi pada jaringan transmisi juga mengakibatkan gangguan pada sistem proteksi dan masalah interference.
Analisis harmonisa dilakukan untuk mengevaluasi efek distorsi dari arus dan tegangan non-sinusoidal pada sistem daya listrik .
Kata Kunci : Sequence Method, Distorsi Harmonisa, Tak-seimbang.
-
1. PENDAHULUAN
Peningkatan pengoperasian beban-beban nonlinier signifikan dengan timbulnya distorsi pada sistem daya. Pada sistem tiga phasa non-linier, elemen-elemen non-linier akan menimbulkan : harmonisa pada rangkaiannya dan mengakibatkan beban menjadi takseimbang yang disebabkan oleh perbedaan nilai parameter tiga phasa, sehingga seketika tegangan masing-masing phasanya akan berbeda. Arus pada masing-masing phasa juga tidak seimbang. Peralatan listrik didesain untuk digunakan pada sistem daya dengan bentuk gelombang sinus murni [1]. Distorsi harmonisa dapat terjadi salah satunya disebabkan oleh beban non-linier seperti : inverter, konverter, peralatan tanur busur listrik, peralatan kontrol, penggerak peubah kecepatan, peralatan elektronik, dll [7] [8] [14 ].
Beban tak seimbang akan memunculkan komponen urutan negatif dan nol. Komponen negatif akan mengakibatkan panas yang berlebihan pada : rotor altenator, penjenuhan trafo, menurunkan torsi dari mesin-mesin listrik AC, dan meningkatkan rugi daya pada jaringan transmisi. Komponen urutan nol dapat menyebabkan meningkatnya rugi-rugi pada jaringan transmisi , dan dapat berpengaruh pada kinerja sistem proteksi dan masalah interference [12].
Bila gelombang arus dan tegangan terdistorsi, keadaan ini akan menyebabkan kondisi tidak normal pada sistem daya listrik. Kadar harmonisa yang
tinggi dalam sistem catu daya listrik tidak dikehendaki karena dapat menimbulkan kerugian [7 ] [8 ] [14 ]. Analisis harmonisa dilakukan untuk mengevaluasi efek distorsi dari arus dan tegangan non-sinusoidal pada sistem daya.
-
2. DASAR TEORI
-
2.1 Metode Urutan
-
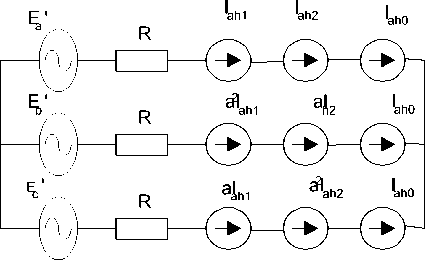
Dalam analisa harmonisa sistem tiga phasa dengan kondisi sumber dalam keadaan seimbang, dihubungkan dengan beban nonlinier yang memiliki karakteristik yang sama. Rangkaian ekuivalen untuk aliran harmonisanya diberikan seperti Gambar 1. Pada sistem tiga phasa non-linier, elemen non-linier akan menimbulkan harmonisa pada rangkaiannya dan mengakibatkan kondisi takseimbang yang disebabkan oleh perbedaan nilai parameter tiga phasanya.

Gambar 1 Model Sistem Daya tiga phasa.
Persamaan rangkaian simetri tiga phasa nonlinier dengan variabel tidak seimbang adalah:
Ua = Um sin ω.t
Ub = Um sin(ω.t - 240o)
Uc = Um sin(ω.t +120o) (1)
Persamaan model sistem daya untuk harmonisa hth dapat dilihat seperti Gambar 2 :
Ua ≠ Ub ≠ Uc, keadaan ini menyebabkan parameter inductor Labc pada rangkaian tiga phasa bentuknya akan menjadi seperti persamaan berikut :
La(Ua(t), ia(t));
Lb(Ub(t), ib(t)); Lc(Uc(t).ic(t))
(2)
Dengan kondisi seperti ini, nilai parameter pada sistem daya tiga phasa akan berubah, dan sistem akan tidak seimbang. Pada keadaan takseimbang harmonisa masing-masing urutan dapat dibagi menjadi komponen urutan positif, negatif dan nol.
Dengan menggunakan teori substitusi, masing-masing inductor seperti pada Gambar (2.1) bisa diganti dengan sumber arus ekuivalen seperti persamaan berikut [1] :
∞
Gambar 2 Equivalen Model Sistem Daya untuk Harmonisa hth
Yi e an
n =1
∞
Σ Ibne
n=1
∞
jnω0t
;
jnω0t
;
(3)
∑ Ine
n=1
Persamaan komponen arus urutan untuk harmonisa hth dapat dibagi menjadi komponen urutan positif, negatif dan urutan nol.. Hubungan komponen urutan
dengan
metode komponen simetri dapat ditulis
seperti :
Iah1
Iah2
Iah0
1
3
1
1
1
a a2
1
a2 a 1
Iah
Ibh
Ich
(4)
I °
a = ej™
; Iah ,
Ibh ,
Ich
: adalah komponen arus
harmonik pada phasa a, b, dan c; sedangkan Iah1 , Iah2 , Iah0 adalah arus urutan positif, negatif, dan nol dari harmonisa hth pada phasa.
Persamaan arus harmonisa untuk phasa b dan phasa c dapat ditentukan :
Ibh 1 = a Iah 1; Ich 1 = aIah 1;
1bh 2 = aIah 2; 1ch 2 = a Iah 2;
Ibh 0 = Ich 0 = Iah 0
2.2 Harmonisa pada sistem tenaga listrik.
Cacat gelombang yang disebabkan oleh interaksi antara bentuk gelombang sinusoidal sistem dengan komponen gelombang lain dikenal dengan harmonisa. THD didefinisikan sebagai persentase total komponen harmonisa terhadap komponen fundamentalnya.
THD tegangannya:
THDV =
∞ 2
L ∑ /h
h = 2
V1
(5)
THD Arusnya adalah :
THDI =
∞
∑ I2
h = 2
(6)
I1
Vh ; Ih = komponen harmonisa. V1 ; I1 = komponen fundamental.
3. METODOLOGI PENELITIAN
Penelitian ini pada sistem dengan 2 bus. Untuk simulasi dipilih beban-beban non linier satu phasa yang di-set dengan nilai parameter yang berbeda. Pengukuran dilakukan hanya pada bus 2. Diagram alir penelitian seperti gambar 3.
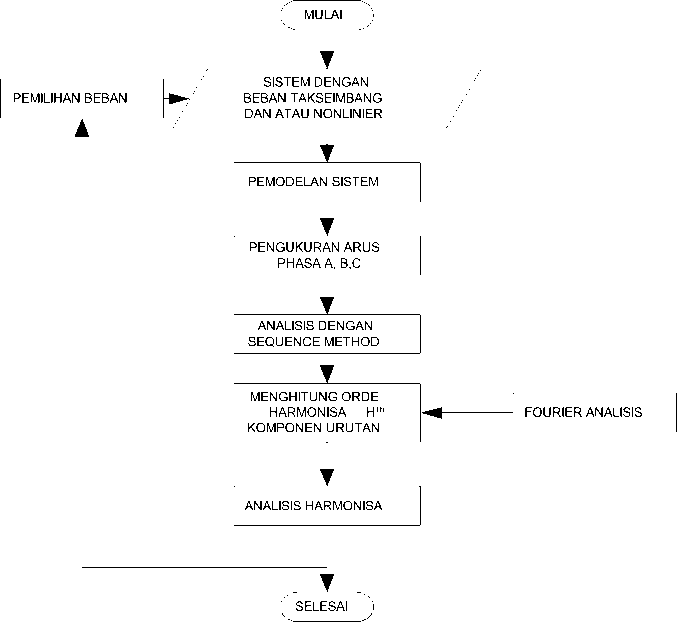
Gambar 3. Metodologi Penelitian
Untuk melakukan study analisa harmonisa digunakan sistem 2 bus dengan 4 kawat seperti Gambar 4.
kVA Base = 10.000kVA ; Impedansi base (pada
-
13.8 kV) = 19 Ω
Data load flow sistem diberikan pada table 1.
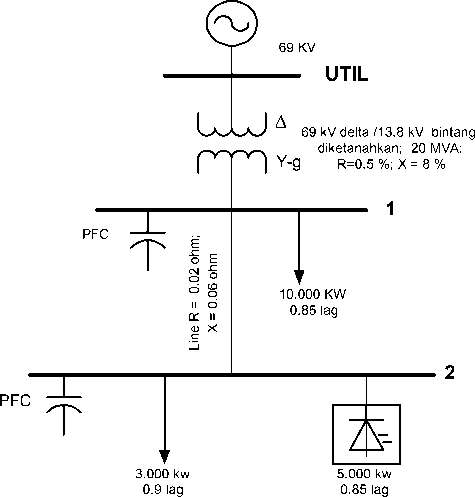
Gambar 4. Single line Diagram Sistem
Tabel 1. Branch data
|
From bus |
To bus |
R (pu) |
X (pu) |
ElementType |
|
UTIL |
1 |
0.0025 |
0.04 |
Transformator |
|
1 |
2 |
0.001 |
0.0032 |
Line |
Tabel 2 Hasil load flow
|
Bus |
P-gen |
Q-gen |
P-load |
Q-load |
Shunt |
V |
Phasa |
|
UTIL |
1.860 |
0.152 |
0 |
0 |
0 |
1.0 |
0.0 |
|
1 |
0 |
0 |
1.0 |
0.62 |
0.62 |
0.922 |
-4.16 |
|
2 |
0 |
0 |
0.8 |
0.455 |
0.455 |
0.991 |
-4.3 |
Dari pemodelan sistem nodal matrik admitansi [Y] dan matrik impedansi [Z] dapat dihitung. Maka bentuk matrik admitansi harmoniknya :
1111
1
Z
Lh
j0.62h
1
-
ZLh
— + — + j0.455h
ZLh ZR2h
Z-Y
Zh Yh
(7)
Tegangan harmonic pada bus 1 dan bus 2 :
V1 h = Zh (1,2) Ich
V = Zh (2,2) Ich (8)

Gambar 5. Sistem Harmonic Impedance
Gambar 5 memperlihatkan driving point dan transfer impedansi yang terjadi seperti pada persamaan (7).
Dari hasil simulasi memperlihatkan pada system terjadi dua resonansi yaitu yang pertama terjadi pada harmonisa ke 5 dan yang kedua pada harmonisa ke 35.

Gambar 6. Sistem Harmonic Voltage
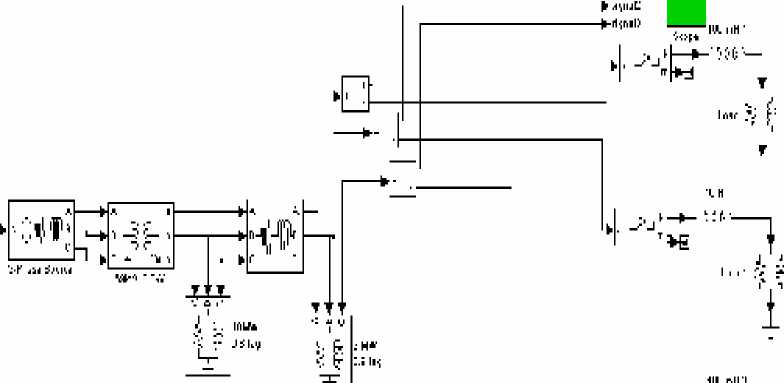
Dengan model sistem sama seperti Gambar 4, disini dibuat beban pada bus 2 dari sistem tidak seimbang dengan memasang beban nonlinier satu phasa dengan nilai parameter berbeda sebanyak 3 buah.
22
⅛1f∏l∣ ^
b«i ⅞ ⅛
I <"k∙J.I Z>rlh^jr
Gambar 7. Diagram Simulink untuk system Tak-seimbang
Orde harmonisa arus untuk Phasa a ( bus 2 )
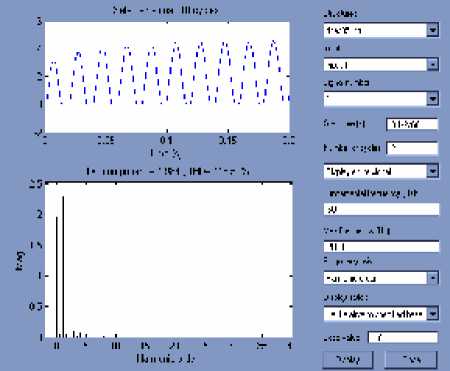
Orde Harmonisa arus untuk Phasa b ( bus 2)
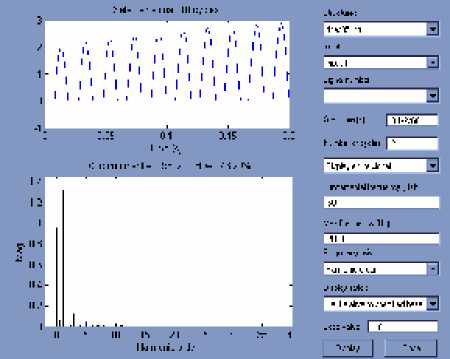
Orde Harmonisa arus untuk Phasa c ( bus 2):
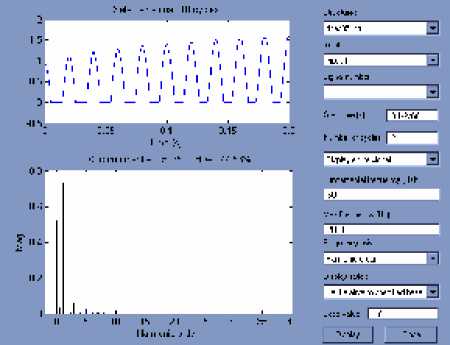
Harmonisa dari masing-masing urutan phasa a Tabel 4.3
|
Urutan Positif |
Urutan Negatif |
Urutan Nol | |||
|
Orde h |
Magnetude |
Orde h |
Magnetude |
Orde h |
Magnet ude |
|
4 |
0.06 |
2 |
0.13 |
3 |
0.11 |
|
10 |
0.01 |
5 |
0.04 |
6 |
0.01 |
|
13 |
0.01 |
8 |
0.02 |
9 |
0.01 |
Harmonisa dari masing-masing urutan phasa b. Tabel 4.4
|
Urutan Positif |
Urutan Negatif |
Urutan Nol | |||
|
Orde h |
Magnetude |
Orde h |
Magnetude |
Orde h |
Magnet ude |
|
4 |
0.01 |
2 |
0.31 |
3 |
0.11 |
|
7 |
0.01 |
5 |
0.04 |
6 |
0.02 |
|
10 |
0.01 |
8 |
0.02 |
9 |
0.0 |
|
13 |
0.01 |
11 |
0.01 |
12 |
0.0 |
Harmonisa dari masing-masing urutan phasa c Tabel 4.5
|
Urutan Positif |
Urutan Negatif |
Urutan Nol | |||
|
Orde h |
Magnetude |
Orde h |
Magnetude |
Orde h |
Magnet ude |
|
4 |
0.01 |
2 |
0.18 |
3 |
0.06 |
|
7 |
0.01 |
5 |
0.02 |
6 |
0.01 |
|
10 |
0.01 |
8 |
0.01 |
9 |
0.0 |
|
13 |
0.0 |
11 |
0.0 |
12 |
0.0 |
Analisis pada sistem daya seimbang cukup hanya menganalisa pada komponen urutan positifnya saja. hasil simulasi memperlihatkan terjadi resonansi pada harmonisa 5 dan 35 , ini disebabkan pada sistem ada terhubung elemen nonlinier.
Analisa harmonisa untuk sistem daya listrik pada kondisi tegangan takseimbang dapat dilakukan pada sistem dengan beban antar phasanya tidak seimbang atau pada sistem dengan beban nonlinier.
Sistem tiga phasa nonlinier akan takseimbang disebabkan oleh parameter tiga phasanya. Karena itu untuk rangkaian harmonisanya dibuat dalam bentuk tiga rangkaian simetri. Ketika elemen nonlinier mengandung n orde harmonik yang terhubung ke sistem, 3n set rangkaian simetri digunakan untuk menggambarkan karakteristik elemen nonlinier tersebut.
-
[1] . Yunping Chen; Qing Chang; Luojiang Qian & Ning Ma,” Studies of the Squence Circuits of Harmonics in Three-Phase Power System” IEEE Transaction on Power Aparatus and System, 2000.
-
[2] . M. Fauri,” Harmonic Modelling of Non-Liniar Load by means of Crossed Frequency Admittance Matrix “, IEEE Transaction on Power Systems, vol. 12, no. 4, November 1997.
-
[3] . J. Lundquist; M.H.J. Bollen,” Harmonic Active Power Flow in Low and Medium Voltage Distribution System “,IEEE Transaction on Power Systems, 2000.
-
[4] . Task Force on Harmonics Modelling and Simulation,” Modelling and Simulation of the Propagation of Harmonics in Electric Power Networks “, IEEE Transaction on Power Delivery, vol. 11, No. 1, January 1996.
-
[5] . R.D. Shultz; R.A. Smith; G.L. Hickey,” Calculation of Maximum harmonic Current and Voltages on Transmition Lines “, IEEE Transaction on Power Apparatus and System , vol. Pas-102, No.4, April 1983.
-
[6] . Ir. Surya Hadi Msc,” Harmonisa dan Pengaruhnya pada Peralatan System Distribusi “, SAINTEK ITM No 10 tahun VI, ISSN: 08544468.
-
[7] . W. Meilczarski; G.J. Anders; M.F. Conlon; W.B. Lawrance; H. Khalsa; G. Michalik,” Quality of Electricity Supply Management of Network Losses “, Melbourne 1997.
-
[8] . R. C. Dugan; M.F. Mc Granaghan,” Electrical Power System Quality “, The McGraw-Hill Companies, 1976.
-
[9] . Irwin Lazar,” Electrical Systems Analysis and Design for Industrial Plants “, McGraw-Hill Company, 1980.
-
[10] . Ding Hongfa; Duan Xiangzhong, “A New Method for Multi-Bus Unbalanced Voltages Synthetic Compensation” IEEE Transaction on Power Aparatus and System, 2000.
-
[11] . Yaw-Juen Wang; Ming-Jer Yang, “ Probabilistic Modeling of Three-phasa Voltage Unbalance Caused by Load Fluctuation”, IEEE Transaction on Power Aparatus and System, 2000.
-
[12] . Ding Hongfa; Duan Xiangzhong, “ A Novel Compensator for Unbalance Three Phase Distribution Feeders”, IEEE Transaction on Power Aparatus and System, 2000.
-
[13] . J. Arrillaga; D.A. Bradley; P.S. Bodger, “ Power System Harmonic”, John Wiley and
Sons, 1985.
-
[14] . Bruce L. Gravis,” Short-Circuit, Coordination, and Harmonic Studies”, IEEE Industry Applications Magazine, March / April 2001.
Teknologi Elektro
57
Vol. 6 No. 1 Januari – Juni 2007
PDF created with pdfFactory Pro trial version www.pdffactory.com
Discussion and feedback