STUDI ALIRAN DAYA JARINGAN DISTRIBUSI 20 KV DI BALI DENGAN METODE YANG LEBIH CEPAT
on
Studi Aliran Daya Jaringan Distribusi ...
I Nyoman Setiawan
STUDI ALIRAN DAYA JARINGAN DISTRIBUSI 20 KV DI BALI DENGAN METODE YANG LEBIH CEPAT
Oleh: I Nyoman Setiawan
Staf Pengajar Program Studi Teknik Elektro, Universitas Udayana Kampus Bukit Jimbaran Bali
Email : setiawan@ee.unud.ac.id
Intisari
Metode analisa aliran daya pada sistem distribusi radial telah banyak dikembangkan. Salah satu metode yang cukup baik telah diusulkan oleh Mekhamer. Metode ini lebih sederhana dari Newton Raphson dari segi
perhitungan iterasi, tidak perlu membentuk admitansi bus dan tidak perlu menggunakan matrik Jacobian.
Kedua metode ini dicobakan pada Penyulang Bukit Jati dan VIP 2 merupakan penyulang-penyulang yang digunakan sebagai obyek analisa aliran daya. Penyulang Bukit Jati adalah penyulang di wilayah Bali Timur, sedangkan Penyulang VIP 2 adalah penyulang di wilayah Bali Selatan.
Hasil analisa dengan metode ini dibandingkan dengan metode Newton Raphson. Metode pendekatan yang digunakan ini lebih cepat, walaupun jumlah iterasi yang diperlukan lebih banyak daripada metode Newton Raphson. Untuk hasil tegangan bus kedua metode menunjukkan hasil yang mendekati sama. Dalam semua analisa, metode ini menunjukkan hasil yang baik, tidak mengalami masalah konvergensi, sehingga analisa aliran daya pada jaringan distribusi 20 kV di Bali dapat deselesaikan dengan baik.
Kata kunci : aliran daya, jaringan distribusi
Perhitungan aliran daya dilaksanakan untuk mendapatkan informasi mengenai aliran daya dan tegangan sistem tersebut. Informasi ini sangat dibutuhkan guna mengevaluasi unjuk kerja sistem tenaga dan menganalisa kondisi pembangkitan maupun pembebanan.
Newton Raphson dan Fast-Decoupled adalah dua metode penyelesaian aliran daya yang biasa digunakan pada sistem tenaga listrik. Dua metode ini lebih sering digunakan, dan dinilai lebih baik dari metode Gauss Seidel untuk sistem yang besar (Sulasno, 1993). Pada kenyataannya, metode aliran daya konvensional (Newton Raphson dan Fast-Decoupled) seringkali tidak mendapatkan hasil perhitungan yang baik atau mengalami masalah pada konvergensi (menjadi divergen) saat digunakan pada jaringan distribusi radial. Masalah ini disebabkan karena rasio R/X pada sistem distribusi radial biasanya adalah besar bila dibandingkan pada sistem transmisi (Mekhamer, 2001).
Untuk menganalisa aliran daya pada sistem distribusi radial, Mekhamer, Soliman, Mostafa, dan El-Hawary mempromosikan suatu metode pendekatan. Metode pendekatan dari Mekhamer dkk adalah suatu pengembangan pada metode aliran daya dari M.E. Baran dan F.F. Wu yang disebut Distflow (Mekhamer dkk, 2001). Metode dari Baran dan Wu berdasarkan pada hukum tegangan dan arus Kirchoff, yang kemudian dimodifikasi sedemikian rupa sehingga menghasilkan tiga perhitungan dasar untuk perhitungan aliran daya, yaitu perhitungan untuk mendapatkan daya real, daya reaktif, dan magnitude tegangan. Rangkaian perhitungan pada metode
Distflow ini kemudian digunakan dalam metode pendekatan, tetapi penggunaan matriks Jacobian pada metode Distflow dihilangkan / dihapus. Iterasi perhitungan pada metode pendekatan oleh Mekhamer dkk dilakukan dengan ide yang sederhana. Perhitungan rugi-rugi daya aktif dan reaktif dijabarkan dalam iterasi, sudut tegangan juga dijabarkan dengan menggunakan hubungan phasor.
Keuntungan menggunakan metode pendekatan ini dibandingkan dengan metode Newton Raphson adalah perhitungannya yang lebih sederhana, tidak perlu membentuk admitansi bus, tidak perlu menggunakan matriks Jacobian dan perhitungan untuk sudut phase lebih sedikit.
Dalam penelitian ini, metode pendekatan digunakan untuk menganalisa aliran daya pada beberapa penyulang 20 kV di Bali dan hasilnya dibandingkan dengan metode Newton Raphson.
Metode pendekatan ini sebelumnya dipresentasikan dan dikembangkan oleh S.F. Mekhamer, S.A. Soliman, M.A. Mostafa, dan M.E. El-Hawary. Metode Pendekatan ini merupakan pengembangan dari metode Distflow, yang sebelumnya telah dikemukakan oleh M.E. Baran dan F.F. Wu. Pada metode ini, Baran dan Wu menentukan tiga perhitungan dasar yang digunakan untuk menyelesaikan analisa aliran daya pada sistem distribusi. Tiga perhitungan dasar itu adalah perhitungan untuk mendapatkan daya aktif, daya reaktif, dan magnitude tegangan. Gambar 1 adalah sistem radial untuk perhitungan Distflow.
Metode Distflow pada jaringan distribusi radial adalah serangkaian perhitungan yang dilakukan untuk bagian sending end dari bus ke-i ( Khedkar dkk, 2003 )
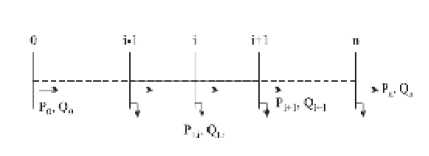
Gambar 1. Sistem Radial Untuk Perhitungan Distflow
22
Vi
22
Vi
-
V+1 = Vi2 -2(riPi + XQi) +
Perhitungan diatas disebut dengan forward equation dan tiap prosesnya disebut dengan forward update. Prosedur dan rangkaian perhitungan yang lain dari Distflow disebut backward update dan backward equation.
Pada metode pendekatan ini nilai-nilai awal P0 dan Q0 ditentukan melalui proses penjumlahan P dan Q beban. V0 adalah tegangan awal yang juga digunakan sebagai tegangan dasar sistem dalam proses perhitungan metode Pendekatan yang menggunakan satuan per-unit.
Dengan asumsi phase seimbang, gambar dari jaringan distribusi radial dapat dilihat pada gambar berikut ini (Mekhamer dkk,2001):
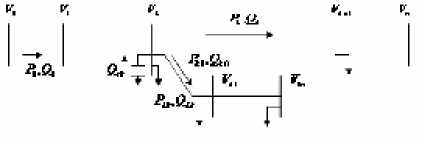
Gambar 2 Model Umum Sistem Distribusi Tipe Radial
Dari gambar, dapat dilihat aliran daya mengalir dengan persamaan sebagai berikut:
P+1 = P -r+ι(P2 + Qi2)/V2 -PLi+1 (4)
Qi+1 = Qi- Xi+1( P2 + Qi2)/V2 - (5)
QLi+1 + Qcm
Vi+1 = V2 -2(r+1 P1 + Xi+1 Qi) + (r+1 + X+1 ∖P2 + Q2)/ V2
(6)
Dengan memasukkan unsur bilangan kompleks, maka magnitude tegangan dan sudut tegangan dari tiap-tiap bus didapat dari persamaan (Fukuyama dkk,2001) :
Vm = Vi-(rM + jx m )(P + jQi)t/ V* (7)
dengan :
r = res stans dari saluran yang menuju bus
x = kapas stans dari saluran yang menuju bus
P = daya real yang mengalir dari bus
Q = daya reaktif yang mengalir dari bus
V = magn tude tegangan pada bus
Qc = tambahan daya reaktif dari kapasitor pada bus
Kondisi berikut harus dipenuhi :
Pada bagian akhir penyulang
P = Qn = 0
Pkn = Qkn = 0
(8)
(9 )
dengan :
Pn= daya aktif pada bus terakhir cabang utama
Qn= daya reaktif pada bus terakhir cabang utama Pkn= daya aktif pada bus terakhir percabangan Qkn= daya reaktif pada bus terakhir percabangan Tegangan pada node k (bus percabangan) dan ko (bus percabangan yang terhubung dengan cabang utama) : Vko = Vk (10)
Rugi-rugi daya pada saluran yang menghubungkan dua bus
Plossi+1 = ri+1(p 2 + Q2)/ V2 (11)
Qlossi+1 = xi+1(p2 + q,2)/ V12 (12)
Untuk val das program, digunakan data yang diambil dari paper Load Flow Solut on of Rad al D str but on Feeders: A New Approach. Hasil yang didapatkan menunjukkan besarnya tegangan, daya aktif dan daya reaktif mendekati sama dengan nilai- nilai tegangan, daya aktif dan daya reaktif yang terdapat dalam paper tersebut.
Data-data yang digunakan dalam melakukan analisis berupa one l ne d agram masing-masing penyulang, daya aktif dan reaktif pada bus beban, kapasitas trafo distribusi serta data penghantar. Bila data yang diperlukan tidak tersedia, maka dilakukan asumsi-asumsi (untuk data pelengkap) dengan memperhatikan kondisi yang ada.
Dalam studi ini dipilih dua penyulang yang dianalisa sebagai sampel, yaitu penyulang Bukit Jati dan Penyulang VIP. Penyulang Bukit Jati adalah penyulang dari GI Gianyar, memiliki 25 trafo
distribusi dengan kapasitas total 2335 kVA. Penyulang VIP 2 adalah penyulang dari GI Sanur, memiliki 19 trafo distribusi dengan kapasitas total 9530 kVA. Hasil analisa dengan metode Pendekatan pada Penyulang Bukit Jati didapatkan besar tegangan masing-masing node seperti ditunjukan pada Tabel 1.
Tabel 1. Tegangan Setiap Bus Penyulang Bukit Jati
|
Bus |
Magnitude (kV) |
Sudut (derajat) |
|
0 |
20 |
0 |
|
1 |
19,856 |
-0,149 |
|
2 |
19,827 |
-0,180 |
|
3 |
19,797 |
-0,211 |
|
4 |
19,794 |
-0,214 |
|
5 |
19,792 |
-0,216 |
|
6 |
19,785 |
-0,223 |
|
7 |
19,751 |
-0,260 |
|
8 |
19,743 |
-0,264 |
|
9 |
19,735 |
-0,268 |
|
10 |
19,699 |
-0,286 |
|
11 |
19,674 |
-0,289 |
|
12 |
19,627 |
-0,295 |
|
13 |
19,624 |
-0,295 |
|
14 |
19,623 |
-0,296 |
|
15 |
19,616 |
-0,297 |
|
16 |
19,611 |
-0,298 |
|
17 |
19,604 |
-0,298 |
|
18 |
19,604 |
-0,299 |
|
19 |
19,601 |
-0,299 |
|
20 |
19,600 |
-0,299 |
|
21 |
19,795 |
-0,214 |
|
22 |
19,789 |
-0,215 |
|
23 |
19,787 |
-0,215 |
|
24 |
19,782 |
-0,216 |
|
25 |
19,780 |
-0,216 |
|
26 |
19,747 |
-0,274 |
|
27 |
19,749 |
-0,261 |
|
28 |
19,735 |
-0,268 |
|
29 |
19,626 |
-0,295 |
|
30 |
19,622 |
-0,295 |
|
31 |
19,621 |
-0,295 |
|
32 |
19,604 |
-0,298 |
|
33 |
19,621 |
-0,295 |
Dengan metode pendekatan ini diperlukan 4 iterasi untuk mencapai konvergen, total daya aktif beban adalah 1984,8 kW, total daya reaktif beban adalah 1230 kVAR, total rugi-rugi saluran 22,362 kW dan
26,551 kVAR, dan waktu analisa adalah 0,04 detik. Sedangkan untuk metode Newton Raphson, dibutuhkan 1 iterasi, total daya aktif beban adalah 1984,8 kW, total daya reaktif beban adalah 1230 kVAR, total rugi-rugi saluran 22,9 kW dan 25,7 kVAR, dan waktu yang dibutuhkan menganalisa adalah 6,489 detik.
Hasil analisa dengan metode pendekatan pada Penyulang VIP didapatkan besar tegangan masing-masing node seperti ditunjukan pada Tabel 2. Iterasi yang dibutuhkan 5 iterasi, total daya aktif beban adalah 8100,5 kW, total daya reaktif beban adalah 5020,2 kVAR, total rugi-rugi saluran 182,58 kW dan 107,48 kVAR, dan waktu yang dibutuhkan menganalisa adalah 0,03 detik. Sedangkan dengan metode Newton Raphson, dibutuhkan 2 iterasi, total daya aktif beban adalah 8100,5 kW, total daya reaktif beban adalah 5020,5 kVAR, total rugi-rugi saluran 182,5 kW dan 107,4 kVAR, dan waktu yang dibutuhkan menganalisa adalah 2,623 detik.
Tabel 2. Tegangan Setiap Bus Penyulang VIP 2.
|
Bus |
Magnitude (kV) |
Sudut (derajat) |
|
0 |
20 |
0 |
|
1 |
19,890 |
0,055 |
|
2 |
19,773 |
0,046 |
|
3 |
19,757 |
0,044 |
|
4 |
19,741 |
0,043 |
|
5 |
19,713 |
0,041 |
|
6 |
19,686 |
0,039 |
|
7 |
19,675 |
0,038 |
|
8 |
19,661 |
0,036 |
|
9 |
19,652 |
0,036 |
|
10 |
19,632 |
0,034 |
|
11 |
19,557 |
0,028 |
|
12 |
19,531 |
0,026 |
|
13 |
19,514 |
0,024 |
|
14 |
19,503 |
0,023 |
|
15 |
19,497 |
0,023 |
|
16 |
19,485 |
0,022 |
|
17 |
19,473 |
0,021 |
|
18 |
19,459 |
0,019 |
|
19 |
19,458 |
0,019 |
Hasil analisa aliran daya metode pendekatan dibandingkan dengan metode Newton Raphson. Hasil perbandingan untuk Penyulang Bukit Jati seperti terlihat pada Tabel 3 dan pada Tabel 4 perbandingan besarnya tegangan setiap node.
Tabel 3 Perbandingan Waktu dan Total Rugi-Rugi Daya
|
Penyulang Bukit Jati | ||||
|
Metode Analisa Daya |
Jumlah Iterasi |
Waktu Yang Dibutuhkan detik |
Total Rugi-Rugi Daya aktif kW |
Total Rugi-Rugi Daya reaktif kVAR |
|
Newton Raphson |
1 |
6,489 |
21,885 |
25,723 |
|
Pendekatan |
4 |
0,04 |
22,362 |
26,551 |
Tabel 4 Perbandingan Magnitude Tegangan
|
Penyulang Bukit Jati | |||
|
Magnitude Tegangan (kV) | |||
|
No Bus |
Newton Raphson |
Pendekatan |
Perbedaan |
|
0 |
20 |
20 |
0 |
|
1 |
19,858 |
19,856 |
0,002 |
|
2 |
19,830 |
19,827 |
0,003 |
|
3 |
19,800 |
19,797 |
0,003 |
|
4 |
19,797 |
19,794 |
0,003 |
|
5 |
19,796 |
19,792 |
0,004 |
|
6 |
19,789 |
19,785 |
0,004 |
|
7 |
19,754 |
19,751 |
0,003 |
|
8 |
19,747 |
19,743 |
0,004 |
|
9 |
19,739 |
19,735 |
0,004 |
|
10 |
19,704 |
19,699 |
0,005 |
|
11 |
19,679 |
19,674 |
0,005 |
|
12 |
19,633 |
19,627 |
0,004 |
|
13 |
19,631 |
19,624 |
0,003 |
|
14 |
19,629 |
19,623 |
0,006 |
|
15 |
19,622 |
19,616 |
0,006 |
|
16 |
19,618 |
19,611 |
0,007 |
|
17 |
19,611 |
19,604 |
0,007 |
|
18 |
19,611 |
19,604 |
0,007 |
|
19 |
19,608 |
19,601 |
0,007 |
|
20 |
19,607 |
19,600 |
0,007 |
|
21 |
19,798 |
19,795 |
0,003 |
|
22 |
19,793 |
19,789 |
0,004 |
|
23 |
19,790 |
19,787 |
0,003 |
|
24 |
19,786 |
19,782 |
0,004 |
|
25 |
19,783 |
19,780 |
0,003 |
|
26 |
19,751 |
19,747 |
0,004 |
|
27 |
19,753 |
19,749 |
0,004 |
|
28 |
19,739 |
19,735 |
0,004 |
|
29 |
19,633 |
19,626 |
0,007 |
|
30 |
19,628 |
19,622 |
0,006 |
|
31 |
19,627 |
19,621 |
0,006 |
|
32 |
19,611 |
19,604 |
0,005 |
|
33 |
19,628 |
19,621 |
0,007 |
Waktu yang dibutuhkan oleh metode pendekatan untuk menganalisa penyulang Bukit Jati
lebih cepat daripada waktu yang dibutuhkan oleh Newton Raphson. Waktu analisa yang lebih lambat dari Newton Raphson disebabkan oleh proses perhitungannya yang melibatkan matriks yang berukuran besar , diantaranya dalam perhitungan P, Q, Jacobian , dan V. Matriks berukuran besar memakan waktu yang lama dalam perhitungan terutama saat melewati perulangan/ loop. Total rugi-rugi daya dengan menggunakan Newton Raphson adalah 21,885 kW (1,1%) dan 25,723 kVAR (2,89%). Untuk perbandingan magnitude tegangan, selisih terbesar dari hasil metode pendekatan dengan Newton Raphson adalah 0,007 kV. Pada Tabel 5 diperlihatkan hasil perbandingan untuk Penyulang VIP 2.
Tabel 5 Perbandingan Waktu dan Total Rugi-Rugi Daya
|
Penyulang VIP 2 | ||||
|
Metode Analisa Daya |
Jumlah Iterasi |
Waktu Yang Dibutuhkan detik |
Total Rugi-Rugi Daya aktif(kW) |
Total Rugi-Rugi Daya reaktif (kVAR) |
|
Newton Raphson |
2 |
2,623 |
182,498 |
107,419 |
|
Pendekatan |
5 |
0,03 |
182,588 |
107,480 |
Waktu yang dibutuhkan oleh metode pendekatan untuk menganalisa penyulang VIP 2 lebih cepat daripada waktu yang dibutuhkan oleh Newton Raphson. Total rugi-rugi daya dengan menggunakan Newton Raphson adalah 182,498 kW (2,25 %) dan 107,419 kVAR (2,14 %). Untuk metode Pendekatan total rugi-rugi dayanya adalah 182,588 kW (2,25 %) dan 107,48 kVAR (2,14 %). Untuk Perbandingan magnitude tegangan, selisih terbesar adalah 0,001 kV seperti terlihat pada Tabel 6.
Tabel 6 Perbandingan Magnitude Tegangan
|
Penyulang VIP 2 | |||
|
Magnitude Tegangan (kV) | |||
|
No Bus |
Newton Raphson |
Pendekatan |
Perbedaan |
|
0 |
20 |
20 |
0 |
|
1 |
19,891 |
19,890 |
0,001 |
|
2 |
19,773 |
19,773 |
0 |
|
3 |
19,757 |
19,757 |
0 |
|
4 |
19,741 |
19,741 |
0 |
|
5 |
19,713 |
19,713 |
0 |
|
6 |
19,686 |
19,686 |
0 |
|
7 |
19,675 |
19,675 |
0 |
|
8 |
19,661 |
19,661 |
0 |
|
9 |
19,652 |
19,652 |
0 |
|
10 |
19,632 |
19,632 |
0 |
|
11 |
19,557 |
19,557 |
0 |
|
12 |
19,531 |
19,531 |
0 |
|
No Bus |
Newton Raphson |
Pendekatan |
Perbedaan |
|
13 |
19,513 |
19,514 |
0 |
|
14 |
19,503 |
19,503 |
0 |
|
15 |
19,497 |
19,497 |
0 |
|
16 |
19,485 |
19,485 |
0 |
|
17 |
19,473 |
19,473 |
0 |
|
18 |
19,458 |
19,459 |
0,001 |
|
19 |
19,457 |
19,458 |
0,001 |
Dalam penelitian ini metode pendekatan dapat diimplementasikan dengan baik pada penyulang 20 kV tipe radial di Bali. Dua penyulang di Bali telah dianalisa dengan metode Pendekatan, semua mencapai nilai konvergen dan didapatkan hasil - hasil analisa yang baik.
Dari hasil pembahasan sebelumnya, maka ada beberapa hal yang dapat disimpulkan yaitu:
-
1. Metode pendekatan yang lebih baru telah dapat diimplementasikan dengan baik pada penyulang 20 kV tipe radial di Bali. Hasil analisa dari dua penyulang di Bali telah didapatkan hasil yang baik dan tidak masalah dalam konvergensi.
-
2. Dari segi waktu, metode pendekatan yang baru dapat menyelesaikan analisa aliran daya lebih cepat dari metode Newton Raphson, walaupun jumlah iterasi yang diperlukan metode ini lebih banyak daripada metode Newton Raphson. Perbandingan hasil analisa aliran daya dari kedua metode yaitu : tegangan, daya tiap bus, dan rugi daya pada saluran, menunjukkan hasil yang mendekati sama. Hal ini menunjukkan metode ini cukup akurat dan relatif bisa diandalkan.
-
5. DAFTAR PUSTAKA
-
[1] . Bayliss, C. 1996. Transmission and Distribution Electrical Engineering. UK: Newness
Publications.
-
[2] . Fukuyama, Y, Naka, S, dan Genji, T . 2001. Practical Equipment Models for Fast Distribution Power Flow Considering
Interconnection of Distributed Generators. IEEE Power Engineering Society Summer Meeting.
-
[3] . Hartojo. 2004. Usaha Penurunan Losses Distribusi Secara Komprehensive. Seminar Losses Energi 2004 PT. PLN(Persero) Distribusi Jateng & DIY – MSEE Teknik Elektro UGM .Proceeding B.
-
[4] . Kashem, M.K, Ganapathy, V, Jasmon, G.B, dan Buhari, M.I . 2000. A Novel Method for Minimization in Distribution Networks.
International Conference on Electric Utility Deregulation and Restructuring Power
Technologies. London: City University.
-
[5] . Khedkar, M.K, Dhole,G.M dan Ingle, V.S. 2003. Optimal Load Transfer : Strategy For Loss Reduction Of Distribution Network. IE(I) Journal-EL Vol : 84 December 2003.
-
[6] . Mekhamer, S.F, Soliman, S.A, Mostafa, M.A dan El-Hawary, M.E. 2001. Load Flow Solution of Radial Distribution Feeders : A New Approach. IEEE Porto Power Tech Conference.
-
[7] . Mok, H.M, Elangovan, S, Salama, M.M.A dan Longjian, C .1999. Power Flow Analysis for Balanced and Unbalanced Radial Distribution System. IEEE Trans. On Power System.
-
[8] . Prasad, K, Sahoo, N.C, Chaturvedi, A, dan Ranjan, R. 2001.A Simple Approach For Branch Current Computation in Load Flow Analysis of Radial Distribution Systems. International Journal of Electrical Engineering Education, http://www1.mmu.edu.my/~nirod diakses pada 12 September 2006
-
[9] . ______. 1987. SPLN 72 : Spesifikasi Desain
Untuk Jaringan Tegangan Menengah (JTM) dan Jaringan Tegangan Rendah. Jakarta : Departemen Pertambangan dan Energi
Perusahaan Umum Listrik Negara.
Teknologi Elektro
1 2
Vol.6 No. 1 Januari –Juni 2007
PDF created with pdfFactory Pro trial version www.pdffactory.com
Discussion and feedback