Pemilihan Lokasi Optimum …

Susiono

PEMILIHAN LOKASI OPTIMUM PEMASANGAN FILTER HARMONIK PADA SISTEM DISTRIBUSI TENAGA LISTRIK TIPE RADIAL

SUSIONO

Staf Pengajar Program Studi Teknik Elektro, Universitas Udayana

Kampus Bukit Jimbaran Bali

Abstrak

Dampak negatip akibat harmonik pada sistem distribusi daya listrik akan menjadi masalah yang sangat serius pada masa yang akan datang. Hal ini terjadi karena semakin meningkatnya penggunaan peralatan listrik berbasis elektronika daya, di masyarakat dalam kehidupan sehari-hari.

Active power line conditioner ( APLC ) adalah filter aktif yang dapat digunakan untuk mereduksi cacat gelombang tegangan sinusoida yang diakibatkan oleh harmonik pada sistem distribusi daya listrik. Masalah yang timbul adalah bagaimana menentukan lokasi pemasangan filter tersebut pada jaringan distribusi bila ada beberapa sumber harmonik dengan orde yang berbeda (multiple source harmonics). Penentuan lokasi pemasangan filter dapat dilakukan dengan pendekatan metode pusat beban,disesuaikan untuk sistem radial tanpa sectionalizer, selanjutnya dilakukan optimasi untuk menentukan arus injeksi dari filter.Simulasi menunjukkan hasil yang cukup baik, cacat harmonik total (THD) lebih dari 9,8% menjadi kurang dari 0,4 %.

Kata kunci : Optimum, filter Harmonik

  • 1.    Pendahuluan.

Harmonik adalah distorsi kontinyu pada gelombang sinusoida pada frekwensi diatasnya sampai 3KHz. Harmonik adalah arus atau tegangan pada frekuensi- frekuensi yang lebih tinggi dari frekuensi dasarnya .

Harmonik ini tidak dikehendaki karena beberapa alasan :

  • a.    Menyebabkan rugi- rugi meningkat.

  • b.    Resonansi rangkaian dapat terjadi pada frekuensi harmonik yang mengakibatkan arus harmonik cukup besar.

  • c.    Alat-alat pengukur menunjukkan harga yang tidak akurat.

  • d.    Pada sistem 3 phasa muncul arus netral harmonik ke tiga.

  • e.    Meningkatkan kemungkinan interferensi dengan rangkaian telekomunikasi.

Sebagai gambaran, pertumbuhan beban nonlinier di Amerika serikat naik dari 5% pada tahun 1960 menjadi 30 % pada tahun 1990 dan pada tahun 2000 diperkirakan 60 %. Dengan analogi yang sama maka jelas beban non-linier di Indonesia akan naik pula.

  • 2.    Sumber-sumber harmonik dan dampak.

    2.1    Bentuk Gelombang Non-Sinusoida.

Bentuk gelombang non-sinusoida dapat terjadi karena 4 sebab dasar, yaitu :

  • 1.    Sumber tegangan atau sumber arus non-sinosoida,     sedangkan    elemen-elemen

rangkaian ( resistor, induktor, kapasitor ) adalah linier ( independent ).

  • 2.    Sumber tegangan atau sumber arusnya sinosoida,     sedangkan    elemen-elemen

rangkaian mengandung elemen non-linier.

  • 3.    Sumber tegangan atau sumber arus non-sinosoida,     sedangkan    elemen-elemen

rangkaian mengandung elemen non-linier.

  • 4.    Sumber tegangan atau sumber arus berupa sumber    DC,    sedangkan    rangkaian

mengandung elemen yang berubah secara periodik.

  • 2.2    Peralatan yang mnjadi sumber harmonik.

Dari beberapa kondisi diatas maka elemen yang dapat dianggap sebagai beban (sumber- sumber harmonik) antara lain :

  • a.    Konverter daya .

  • b.    Inverter.

  • c.    Tanur listrik (Arc Furnace).

  • d.    Ketidak linieran magnetisasi trafo.

  • e.    Peralatan listrik dengan kontrol elektronik.

Tabel 1 Rata-rata Harmonik ( % ) pada Tanur listrik [6]

ORDE

LEVEL

Refining 7

Refining 5

Refining 6

2

3.2

4.1

4.5

3

4

4.5

4.7

4

1.1

1.8

2.8

5

3.2

2.1

4.5

6

0.6

not given

1.7

7

1.3

1

1.6

8

0.4

1

1.1

9

0.5

0.6

1

10

> 0.5

> 0.5

> 1

Tabel 2 Besarnya Arus Harmonik berbagai jenis TV[6]

ORDE

TIPE TV/ ARUS ( AMPERE )

Warna, Thyristor

Warna, Dioda

3

0.82

0.73

5

0.66

0.59

7

0.34

0.43

9

0.14

0.27

11

0.09

0.15

15

0.04

0.045

  • 2.3    Dampak harmonik terhadap sistem jaringan distribusi.

Dampak negatip yang ditimbulkan adanya tegangan dan arus harmonik terhadap sistem distribusi adalah :

  • i.    Penguatan terhadap tingkat harmonik tertentu yang dihasilkan karena adanya resonansi seri atau resonansi paralel.

  • ii.    Penurunan efisiensi pembangkit, transmisi / distribusi dan utilitas.

  • iii.    Penuaan isolasi komponen sistem sehingga menurunkan usia pakai peralatan.

  • iv.    Kesalahan operasi perangkat.

  • 3    Cara mengendalikan harmonik

Pada dasarnya harmonik menjadi masalah jika:

  • 1.    Sumber arus-arus harmonik terlalu besar.

  • 2.    Lintasan dimana arus mengalir sangat panjang sehingga mengakibatkan distorsi tegangan yang melampaui standar atau interferensi terhadap komunikasi.

  • 3.    Respon dari sistem menunjukkan satu atau lebih harmonik-harmonik

Apabila masalaha ini muncul, maka langkah dasar pemilihan untuk mengontrol harmonik adalah:

  • 1.    Mereduksi    arus-arus    harmonik    yang

dihasilkan oleh beban.

  • 2.    Memasang filter untuk menjebak arus-arus harmonik     keluaran     dari     sistem,

membatasinya dari sistem yang lain.

  • 3.    Merubah respon frekuensi dari sistem dengan filter,induktor dan kapasitor.

Beberapa fasilitas teknik yang dapat digunakan untuk mengontrol harmonik antara lain:

  • a.    Filter shunt

  • b.    Kompensasi Harmonik atau injeksi

  • 3.1    Kompensasi harmonik atau Injeksi Harmonik

Arus-arus harmonik dapat dikurangi dengan menginduksikan fluksi harmonik di dalam inti trafo dengan penggeseran phasa 1800 dari fluksi yang diinduksikan oleh arus harmonik yang melalui sekunder trafo.

Adaptif kompensator ini didesain untuk memonitor arus harmonik secara tetap (kontinyu) dan mengijeksikan arus yang sama dan berlawanan phasa

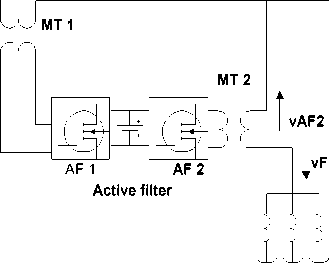
terhadap komponen distorsi dan menghilangkannya (cancel). Alat ini sering pula disebut sebagai active power line conditioner . Rangkaian utama dari alat ini adalah terdiri dari dua filter aktif AF1 dan AF2 ,trafo penyesuai (matching transformer) MT1dan MT2 dan pasif filter PF, seperti ditunjukkan pada gambar 1 [2]:

Filter aktif AF1 dihubungkan seri dengan sumber tegangan melalui trafo MT1 sedangkan AF2 dihubungkan seri dengan filter pasif melalui trafo MT2.

Tiap filter aktif terdiri dari 3 buah inverter PWM satu phase(memakai Mosfet), terminal DC dari enam inverter 1 phase masing-masing dihubungkan dengan kapasitor. Filter pasif ditala pada frekuensi 5 dan 7,11 dan 13.Dalam penggunaan praktisnya suatu filter pasif ditala pada frekuensi 5 dan 7 dari frekuensi dasarnya karena dalam sistem daya, harmonik paling dominan adalah ke 5 dan 7

  • 3.3    Metode penentuan lokasi filter pada jardis.

Untuk menentukan lokasi pemasangan filter pada jaringan dapat digunakan metode pusat beban; (momen pusat) menggunakan pendekatan seperti berikut ini :

I tot

I 2


I 3

Gambar -2. Pusat beban

Perhitungan dilakukan sebagai berikut: nh

ΣΣ (LnIhn)

L = n=1 h =2______________ (1 )

n

Σ In n=1

dengan :

L =jarak titik referensi ( suplai tegangan )   ke

lokasi filter

Ln = Jarak titik referensi ke titik pengukuran harmonik pada titik ( bus ) n.

I nh = arus pada titik pengukuran ke n untuk harmonik ke h .

Pada metode momen pusat ini, ditentukan agar dapat membentuk servis area, dimana tegangan ujung saluran diusahakan merata besarnya. Sehingga perbedaan tegangan pada semua bagian saluran tidak terlalu besar.


vAF1


i S


vB


5th 7th HP

Pasive Filter


i L1 I


L1 Harmonic Sensitive Load


iL2


iL3



L2

Unidentified Harmonic producing Load


L3 Identified Harmonic producing Load


Gambar - 1 active power line conditioner

  • 3.4    Model jaringan distribusi.

Model jaringan distribusi yang akan dijadikan obyek penelitian diasumsikan seperti gambar 3 dengan data impedansi ,data pengukuran tegangan dan arus distorsi harmonik diasumsikan seperti pada table-tabel berikut :

  • 3.5    Menentukan besarnya arus injeksi filter.

Setelah lokasi filter didapatkan melalui pendekatan metode diatas, selanjutnya dihitung besarnya arus injeksi dari filter dengan non-linier programming, yaitu dengan meminimalkan jumlah distorsi tegangan ( THD ) setelah diberikan arus injeksi dari filter kepada masing-masing Bus.

Jika besarnya tegangan harmonik sebelum filter dipasang adalah = v dan reduksi distorsi tegangan = Δv, maka model pendekatan yang dapat dipergunakan untuk menentukan besarnya distorsi tegangan setelah filter harmonik dipasang adalah:

  • 3.6    Menentukan besarnya arus injeksi filter.

Setelah lokasi filter didapatkan melalui pendekatan metode diatas, selanjutnya dihitung besarnya arus injeksi dari filter dengan non-linier programming, yaitu dengan meminimalkan jumlah distorsi tegangan ( THD ) setelah diberikan arus injeksi dari filter kepada masing-masing Bus

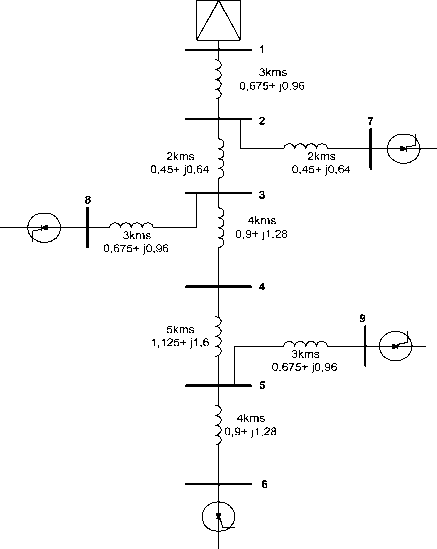
Gambar- 3 Model Simulasi Sistem Distribusi


Jika besarnya tegangan harmonik sebelum filter dipasang adalah = v dan reduksi distorsi tegangan = Δ v, maka model pendekatan yang dapat dipergunakan

untuk menentukan besarnya distorsi tegangan setelah filter harmonik dipasang adalah:

HK     MM

h      hi         h      hr

I - XI )]2) km   m       km   m


(2 )


Min = ( hr            h hr h hi 2 + hi

v ∕ . ∕ . [ vk ∕ . (Rkm Im + Xlim Im )]    [ v k + ∕ (R

h=2 k=1           m=1

subyect to

MM

hr                        hr             h hi 2 hi                          hi            h hr 2 0.5 h

m=1

H          M                                   M0.5

hr              h hr h hi 2 hi              h hi h hr 2

^.U vk + ∕ (RkmIm - XkcrnIm )] + [ vk  + ∕ (RkmIm - XkcrnIm )]}[ ≤ THD k

dengan:

H = total orde harmonik

K = total jumlah bus

Vkh = tegangan harmonik pada bus k untuk harmonik ke h setelah dipasang filter.

M = total jumlah bus kandidat yang akan dipasang filter

Imhr = bagian riil arus filter pada bus kandidat m untuk harmonik ke h.

Imhi = bagian imajiner arus filter pada bus kandidat m untuk harmonik ke h.

h

Vk = batas tegangan untuk harmonik ke h pada bus k , biasanya ( 3 % ) THDk = THD pada bus k.

Tabel -1: Hasil Pengukuran Tegangan Harmonik (asumsi)

NO. BUS

TEGANGAN HARMONIK ( % )

H=5

Sudut

H=7

Sudut

H=9

Sudut

THD

1

6,1

79

5,0

59

4,8

32

9,23

2

6,0

62

6,0

21

5,3

75

10,004

3

7,0

-52

6,0

92

3,6

45

9,89

4

7,5

26

5,0

84

2,7

40

9,41

5

5.0

17

6,0

85

3,5

64

8,55

6

8,8

49

4,7

30

3,5

30

10,57

7

8,2

30

5,5

25

2,6

40

10,21

8

4,7

40

5,5

57

2,8

59

7,75

9

8,2

49

2,3

70

1,8

45

8,7

Tabel -2 : Hasil Pengukuran Arus Harmonik (asumsi)

NO.

BUS

ARUS HARMONIK ( % )

H=5

Sudut

H=7

Sudut

H=9

Sudut

THD

6

10

59

15,0

29

4,8

32

18,65

7

10

62

16,0

21

5,3

75

19,59

8

7,0

60

6,0

92

3,6

45

9,89

9

8,5

26

5,0

84

2,7

40

10,22

Tabel -3: Impedansi Saluran orde H = 5

Bus

1

2

3

4

5

6

7

8

9

1

0.00

0.675+j4.84

1.125+j8

2.025+j14.4

3.15+j22.4

3.825+j27.

1.125+j8

1.8+j12.8

3.825+j27.

2

0.675+j4.84

0.00

0.45+3.2

1.35+j9.6

2.475+j17.

3.375+j24

0.45+j3.2

1.125+j8

3.15+j22.4

3

1.125+j8

1.125+j8

0.00

0.9+j6.4

2.025+j14.

2.925+j20.

2.925+j20.

0.675+j4.8

2.7+j19.2

4

2.025+j14.4

1.35+j9.6

0.9+j6.4

0.00

0.9+j6.4

2.025+j14.

0.9+j6.4

1.575+j11.

1.8+j12.8

5

3.15+j22.4

2.475+j17.6

2.025+j14.4

0.9+j6.4

0.00

0.9+j6.4

2.925+j20.

2.7+j19.2

0.675+j4.8

6

3.825+j27.2

3.375+j24

2.925+j20.8

2.025+j14.4

0.9+j6.4

0.00

3.825+j27.

3.6+j25.6

1.575+j11.

7

1.125+j8

0.45+j3.2

2.925+j20.8

0.9+j6.4

2.925+j20.

3.825+j27.

0.00

1.575+j11.

3.6+j25.6

8

1.8+j12.8

1.125+j8

0.675+j4.8

1.575+j11.2

2.7+j19.2

3.6+j25.6

1.575+j11.

0.00

3.375+j24

9

3.825+j27.2

3.15+j22.4

2.7+j19.2

1.8+j12.8

0.675+j4.8

1.575+j11.

3.6+j25.6

3.375+j24

0.00

  • 4.    Hasil Analisis dan Simulasi.

Perhitungan momen pusat :

(5x19,59)+(8x9,89)+(17x1 Q22)+(18r1 865)
--------------------------------=1176kms 19,59+9,89+1022+1865

Lokasi filter harmonik optimum adalah pada jarak 11,76 kms dari bus 1, yaitu terletak diantara bus 4 dan bus 5. Setelah lokasi ini ditentukan ,misalnya pada Bus 4 selanjutnya dilakukan optimasi arus injeksi dan menghitung distorsi tegangan setelah dilakukan pemasangan filter.

  • 5.    Kesimpulan

  • 1.    Model pusat beban dapat digunakan untuk menentukan lokasi filter harmonik pada system distribusi radial tanpa sectionalizer atau tiap seksi ( zone ) pada saluran distribusi atau menentukan lokasi filter pada sekelompok beban yang terdiri dari beberapa beban non-linier, dimana dikehendaki hanya memasang sebuah filter saja.

  • 2.    Dengan memasang filter harmonik pada lokasi yang optimum, cacat harmonik total dapat dikurangi    sehingga    bentuk    gelombang

  • tegangannya mendekati sinusoida.

  • 6. Daftar Pustaka

  • [1] . Andrew Roe, User Guide for LINDO and LINGO – Windows Version, Duxbury Press, California, 1997.

  • [2] . Hirofumi Akagi, A New Power Line Conditioner for Harmonic Compensation in Power System, IEEE.Trans on Power Delivery, Vol 10, No: 3, July 1995, p. 1570.

  • [3] . Hirofumi Akagi, Control Strategy and Site Selection of Shunt Active Filter for Dumping of Harmonic Propagation in Power Distribution, IEEE.Trans on Power Delivery, Vol 12, No: 1, Jan 1997.

  • [4] .   Hong. Y.Y, Chang. Y.K, Determination of

Location   and Sizes for Active Power Line

Conditioner to Reduce Harmonics in Power System, IEEE. Trans on Power delivery, vol 11, No:3, July 1996, p.1610.

  • [5] . IEEE Recommended Practices and Recuirements for Harmonics control In Electrical Power Syatem, IEEE std 519- 1992.

  • [6] . J. Arrillaga, D.A. Bradley, P.S. Bodger, Power Syatem Harmonics, John Welley & Sons, 1985.

  • [7] . Susiono, Penentuan Lokasi Filter Harmonik Optimum pada Sistem Distribusi Tenaga Listrik, ITS, 1999.

Teknologi Elektro

1 3

Vol. 5 No. 1 Januari – Juni 2006

PDF created with pdfFactory Pro trial version www.pdffactory.com