APLIKASI SIMULASI MONTE CARLO UNTUK MENENTUKAN KEANDALAN SISTEM DISTRIBUSI PRIMER TENAGA LISTRIK
on
Aplikasi Simulasi Monte Carlo …
Manuaba, Sukerayasa, Satriya Utama
APLIKASI SIMULASI MONTE CARLO UNTUK MENENTUKAN KEANDALAN SISTEM DISTRIBUSI PRIMER TENAGA LISTRIK
IBG Manuaba, I Wayan Sukerayasa, Ngakan P Satriya Utama Staff pengajar Teknik Elektro Universitas Udayana
Kampus bukit Jimbaran Bali
Abstrak
Meningkatnya kebutuhan akan tenaga listrik, menuntut suatu sistem tenaga listrik yang mempunyai keandalan yang tinggi dalam penyediaan dan penyaluran dayanya. Untuk mengetahui keandalan penyaluran tenaga listrik, perlu diperhitungkan indeks keandalannya. Untuk mendapatkan indeks keandalan pada penyulang-penyulang pada GI. Padang Sambian digunakan metode Simulasi Monte Carlo (SMC). Metode ini adalah suatu prosedur simulasi untuk memperoleh indeks keandalan dengan memakai bilangan acak. SMC disimulasikan melalui program yang dibangun dalam Bahasa Pemrograman Matlab v6.1.Hasil simulasi menghasilkan indeks jangka waktu kegagalan (r) yang nilainya hampir sama yaitu 3,0 jam/kegagalan sedangkan indeks frekwensi kegagalan ( λ ) dan indeks ketidaktersediaan (U) nilainya bertambah besar apabila saluran bertambah panjang. Besarnya indeks sistem SAIFI = 1.88975, SAIDI = 5.702071, CAIDI = 3.01736, ASAI = 0.99935 dan ASUI = 0.00065. Histogram indeks keandalan menunjukkan bahwa indeks berbeda setiap tahun.
Kata Kunci : Keandalan, Sistem distribusi tenaga listrik, Simulasi Monte Carlo
Kebutuhan akan tenaga listrik sejalan dengan semakin meningkatnya taraf hidup masyarakat. Meningkatnya kebutuhan akan tenaga listrik, menuntut suatu sistem tenaga listrik yang mempunyai keandalan dalam penyediaan dan penyaluran dayanya. Dalam penyaluran tenaga listrik dari Gardu Induk ke pusat-pusat beban diperlukan saluran distribusi. Untuk mengetahui keandalan dalam penyaluran tenaga listrik kepada para konsumen, perlu diperhitungkan indeks keandalannya. Indeks keandalan adalah merupakan suatu indikator keandalan yang dinyatakan dalam suatu besaran probabilitas. [1]
Teknik yang digunakan dalam evaluasi keandalan sistem tenaga listrik dapat dibagi menjadi dua kategori dasar yaitu metode analisis dan metode simulasi. Teknik analisis telah dikembangkan dan telah digunakan pada beberapa dekade terakhir ini. Teknik analisis menggambarkan sistem sebagai model matematika dan mengevaluasi indeks keandalan dari model ini dengan menggunakan solusi matematika. Teknik analisis umumnya digunakan untuk mengevaluasi nilai tengah atau nilai perkiraan dari titik beban dan indeks keandalan sistem. Namun nilai tengah tidak menyediakan informasi apapun atas variabilitas dari indeks, sedangkan probabilitas distribusi menyediakan suatu penyajian bergambar atas daerah indeks yang berubah-ubah walaupun terjadi sangat jarang tetapi dapat mempunyai efek sistem yang sangat serius. Teknik simulasi dapat menentukan probabilitas dari indeks. Berdasarkan hal-hal tersebut di atas, maka dilakukan suatu evaluasi keandalan jaringan distribusi melalui suatu pendekatan Simulasi Monte Carlo yang menyediakan kesempatan untuk mengembangkan suatu
pengetahuan dan informasi dari variabilitas yang berhubungan dengan indeks tahunan.
Sehingga dengan membahas evaluasi keandalan penyulang 20 kV dengan metode Simulasi Monte Carlo dapat diketahui indeks keandalan titik beban dan indeks keandalan sistem yang sangat berguna untuk perencanaan sistem.
Indeks keandalan merupakan suatu indikator keandalan yang dinyatakan dalam suatu besaran probabilitas Sejumlah indeks sudah dikembangkan untuk menyediakan suatu kerangka untuk mengevaluasi keandalan sistem tenaga. Evaluasi keandalan sistem distribusi terdiri dari indeks titik beban dan indeks sistem. Indeks kegagalan titik beban yang biasanya digunakan meliputi tingkat kegagalan λ (kegagalan/tahum), rata-rata waktu keluar (outage) r (jam/kegagalan) dan rata-rata ketidaktersediaan tahunan U (jam/tahun). [3]
Nilai rata-rata dari ketiga indeks titik beban dasar untuk titik beban j dapat dihitung dari sejarah operasi (up-down) dari titik beban dengan menggunakan persamaan sebagai berikut:
j Σ Tuj
=ΣTj
j Nj
ΣT
U'~Σ Tj+Σ Tj
(1)
-
(2)
-
(3)
Di mana ∑ Tu j dan ∑ Td j menghadirkan total uptime dan downtime untuk titik beban j dan N j menghadirkan banyaknya kegagalan sepanjang periode simulasi untuk titik beban j.
Dalam menentukan probabilitas distribusi dari frekwensi kegagalan titik beban, nilai periode k dari indeks ini dihitung untuk masing-masing sampel tahun. m(k) adalah nomor tahun dimana terjadi frekwensi outage titik beban sama dengan k. Probabilitas distribusi p(k) dari frekwensi kegagalan titik beban dapat dihitung menggunakan persamaan sebagai berikut:
m(k)
-
p(k) = (4)
M
dimana: k = 0,1,2,...
Di mana M adalah total sampel tahun. Probabilitas distribusi dari ketidaktersediaan titik beban distribusi dapat dihitung dalam suatu cara yang serupa. Untuk mengkalkulasi probabilitas distribusi dari jangka waktu outage, dihitung jumlah kegagalan n(i) dengan jangka waktu outage antara i - 1 sampai i. Probabilitas distribusi p(i) dapat dihitung dengan menggunakan persamaan sebagai berikut:
-
p(i) =n(i) (5)
N
dimana: i = 1,2,3,...
Di mana N adalah total kegagalan didalam sampel tahun. Indeks sistem dapat dihitung dari indeks titik beban dasar seperti indeks sistem pada dasarnya adalah bobot rata-rata beban dari nilai titik beban individu. Distribusi dari indeks sistem dapat juga diperoleh dari periode indeks titik beban. Berdasarkan pada indeks titik beban pada persamaan (1) dan (2), indeks keandalan sistem dievaluasi sebagai berikut :
-
a. System Average Interruption Frequency Index
(SAIFI)
Indeks ini didefinisikan sebagai jumlah rata-rata kegagalan yang terjadi per pelanggan yang dilayani oleh sistem per satuan waktu (umumnya per tahun).
λM
SAIFI = k k (6)
∑ Mk
-
b. System Average Interruption Duration Index (SAIDI)
Indeks ini didefinisikan sebagai nilai rata-rata dari lamanya kegagalan untuk setiap konsumen selama satu tahun.
UM
SAIDI = k k (7)
∑ Mk
-
c. Customer Average Interruption Duration Index (CAIDI)
Indeks ini didefinisikan sebagai lamanya kegagalan untuk pelanggan yang mengalami gangguan selama satu tahun.
UM
CAIDI = k k (8)
∑Mkλk
-
d. Average Service Availability Index (ASAI)
Indeks ini adalah perbandingan dari jumlah total waktu pelanggan yang dapat dilayani selama satu tahun terhadap total permintaan waktu pelanggan.
M ∗8760- M U
ASAI = k k k (9)
∑Mk∗8760
dimana Mk adalah banyaknya pelanggan di titik beban k.
-
e. Average Service Unavailability Index (ASUI)
Indeks ini adalah nilai pelengkap dari ASAI yang mungkin kadang-kadang diperlukan.
ASUI=1-ASAI (10)
Kegunaan dari informasi indeks keandalan sistem adalah sangat luas, kegunaan-kegunaan yang paling umum meliputi:.
-
1. Melengkapi manajemen dengan data capaian mengenai mutu layanan pelanggan pada sistem listrik secara keseluruhan.
-
2. Untuk mengidentifikasi subsistem dan sirkit dengan capaian di bawah standard dan untuk memastikan penyebabnya.
-
3. Melengkapi manajemen dengan data capaian mengenai mutu layanan pelanggan untuk masing-masing area operasi.
-
4. Menyediakan sejarah keandalan dari sirkit individu untuk diskusi dengan pelanggan sekarang atau calon pelanggan.
-
5. Memenuhi syarat pelaporan pengaturan.
-
6. Menyediakan suatu basis untuk menetapkan ukuran-ukuran kesinambungan layanan.
-
7. Menyediakan data capaian yang penting bagi suatu pendekatan probabilistik untuk studi keandalan sistem distribusi.[4]
Simulasi Monte Carlo (SMC) adalah suatu teknik stokastik yang digunakan untuk memecahkan permasalahan matematika. Kata “Stokastik” berarti bahwa Simulasi Monte Carlo menggunakan angka-angka acak dan probabilitas statistik untuk memperoleh suatu jawaban. Metoda Monte Carlo mula-mula dikembangkan untuk proyek Manhattan selama Perang Dunia II. Bagaimanapun, Simulasi Monte Carlo kini diberlakukan bagi suatu cakupan yang luas tentang permasalahan-permasalahan disain reaktor nuklir, ekonometrik, evolusi mengenai bintang, meramalkan bursa saham dan lain lain. [5]
Bagian penting dari Simulasi Monte Carlo adalah pemahaman tentang angka acak mulai dari menghasilkannya dan mengkonversinya. Dalam distribusi eksponensial yang mempunyai laju kegagalan (λ ) yang konstan dan variasi eksponensial dari T ditunjukkan dalam persamaan 2.15 berikut:
T = - 1ln( X) (11)
λ
Dimana X adalah angka acak yang nilainya antara 0 sampai 1. Pembuatan angka acak ini umumnya dibantu oleh program komputer. Dalam keandalan jaringan distribusi, angka acak ini dipakai untuk mendapatkan nilai TTF dan TTR sesuai nilai rata-ratanya. Nilai TTF dan TTR didapatkan dengan mengkonversikan nilai X kedalam persamaan, sehingga persamaan 2.15 akan menjadi:
TTF = - MTTF ln( X) (12)
TTR = - MTTR ln( X) (13)
Proses yang digunakan untuk mengevaluasi indeks keandalan sistem distribusi yang menggunakan Simulasi Monte Carlo terdiri dari langkah-langkah sebagai berikut:
-
1. Hasilkan sebuah angka acak untuk masing-masing elemen didalam sistem dan mengkonversinya ke dalam TTF yang sesuai dengan probabilitas distribusi dari parameter elemen tersebut.
-
2. Tentukan elemen dengan TTF minimum.
-
3. Hasilkan sebuah nomor acak dan
konversikan nomor ini ke dalam Repair Time (RT) dari elemen dengan TTF minimum menurut probabilitas distribusi dari waktu perbaikan.
-
4. Hasilkan angka acak yang lain dan konversi nomor ini ke dalam Switch Time (ST) menurut probabilitas distribusi dari Switch Time jika tindakan ini mungkin.
-
5. Gunakan prosedur “penentuan kegagalan titik beban” dan rekam jangka waktu keluar (outage) untuk masing-masing titik beban yang gagal.
-
6. Hasilkan sebuah angka acak yang baru untuk elemen yang gagal dan konversikan kedalam suatu TTF baru, dan kembali ke langkah 2 jika waktu simulasi kurang dari satu tahun. Jika waktu simulasi lebih besar dari satu tahun, langsung ke langkah 9.
-
7. Kalkulasi jumlah dan jangka waktu kegagalan untuk masing-masing titik beban untuk masing-masing tahun.
-
8. Kalkulasi nilai rata-rata dari jangka waktu kegagalan titik beban untuk sampel tahun.
-
9. Kalkulasi indeks sistem dan rekam indeks-indeks ini untuk masing-masing tahun.
-
10. Kalkulasi nilai rata-rata dari indeks-indeks sistem ini.
-
11. Kembali ke langkah 2 jika waktu simulasi kurang dari total tahun simulasi yang ditetapkan, jika tidak keluarkan hasil. [2]
Data Standar PLN yang digunakan dalam simulasi adalah Standar PLN 59 : “Kandalan pada Sistem Distribusi 20 kv dan 6 kV”, yaitu: [10]
-
- λ saluran = 0.2 /km.tahun
-
- λ trafo = 0.005 /unit.tahun
-
- MTTR saluran = 3 jam
-
- MTTR trafo = 10 jam
Penyulang-penyulang pada Gardu Induk Padang Sambian ditunjukkan pada gambar 1 berikut:
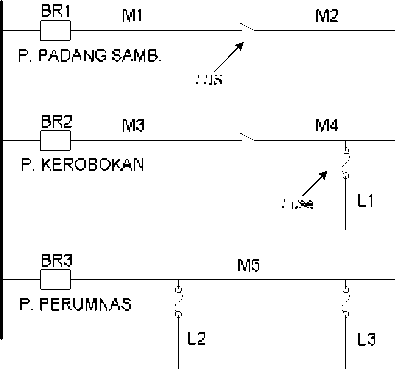
Gambar 1 Penyulang pada GI. Padang Sambian
Data panjang saluran dan jumlah titik beban pada masing-masing saluran ditunjukkan pada tabel 1. Setelah program disimulasikan maka dapat dihasilkan Indeks titik beban untuk masing-masing titik beban pada GI Padang Sambian yang ditunjukkan dalam tabel 2. Tanda “:” pada tabel 2 menunjukkan bahwa semua baris diantara tanda “:” mempunyai nilai yang hampir sama. Dalam tabel 3 menunjukkan nilai dari indeks keandalan sistem. Gambar 2 sampai gambar 5 menunjukkan histogram dari indeks keandalan titik beban dan gambar 6 sampai gambar 10 menunjukkan histogram dari indeks keandalan sistem.
Tabel 1 Data panjang saluran Penyulang pada GI. Padang Sambian
|
Saluran |
Panjang (meter) |
Jumlah titik beban |
Kode Gardu Distribusi |
|
M1 |
7041 |
15 |
DB.225, DB.442, DB.352, DB.084, DB.083, DB.237, DB.187, DB. , DB.119, DB.328, DB.471, DB.275, DB. , DB.316, DB.112 |
|
M2 |
6670 |
25 |
DB.304, DB.128, DB.145, DB.214, DB.369, DB.413, DB.468, DB.203, DB.391, DB. , DB.467, DB. 113, DB.259, DB. 472, DB.327, DB.386, DB.114, DB.244, DB. , DB.419, DB. 116, DB.343, DB.115, DB.355, KA.738 |
|
M3 |
8165 |
13 |
KA.736, KA.085, KA.418, DB.356, DB.175, DB.201, DB.088, DB.243, DB.207, DB.279, KA.263, KA.092, KA.083 |
|
M4 |
8014 |
16 |
KA.108, KA.086, KA.087, KA.532, KA.772, KA.084, KA.318, KA., KA.088, KA.089, KA.866, KA.608, KA.417, KA.578, KA.562 |
|
M5 |
6339 |
14 |
DB.403, DB.417, DB.149, DB.224, DB.318, DB.064, DB.065, DB.363, DB. , DB.427, DB.218, DB.225, DB.257, DB.061 |
|
L1 |
1115 |
3 |
KA.589, KA.713, KA.533 |
|
L2 |
310 |
4 |
DB.063, DB.461, DB.235, DB.645 |
|
L3 |
842 |
4 |
DB.124, DB.062, DB.323, DB.408 |
Sumber: One Line Diagram GI. Padang Sambian, PT. PLN (Persero) AJ Bali Selatan
Tabel 2 Indeks titik beban hasil program Simulasi Monte Carlo untuk GI. Padang Sambian
|
No |
Gardu |
λ (kegagalan/tahun) |
r (jam/kegagalan) |
U (jam/tahun) |
Penyulang |
Saluran |
|
1 |
DB.225 |
1.2385019 |
3.0446588 |
3.7691934 |
Padang Sambian |
M1 |
|
15 |
DB.112 |
1.2383515 |
3.0428349 |
3.766479 |
Padang Sambian |
M1 |
|
16 |
DB.304 |
2.4210617 |
3.0245752 |
7.3165668 |
Padang Sambian |
M2 |
|
40 |
KA.738 |
2.4216146 |
3.027649 |
7.3256678 |
Padang Sambian |
M2 |
|
41 |
KA.736 |
1.531148 |
3.0327584 |
4.6411417 |
Kerobokan |
M3 |
|
53 |
KA.083 |
1.531098 |
3.0329614 |
4.6413007 |
Kerobokan |
M3 |
|
54 |
KA.108 |
3.0129643 |
3.0085338 |
9.0552348 |
Kerobokan |
M4 |
|
68 |
KA.562 |
3.0124589 |
3.0104254 |
9.0654237 |
Kerobokan |
M4 |
|
69 |
KA.589 |
3.2376923 |
3.0102148 |
9.7353182 |
Kerobokan |
L1 |
|
71 |
KA.533 |
3.2377915 |
3.0093532 |
9.7328327 |
Kerobokan |
L1 |
|
72 |
DB.403 |
1.1724171 |
3.0053972 |
3.5221624 |
Perumnas |
M5 |
|
85 |
DB.061 |
1.1715659 |
3.0018743 |
3.5154821 |
Perumnas |
M5 |
|
86 |
DB.063 |
1.2330159 |
3.0072015 |
3.7063584 |
Perumnas |
L2 |
|
89 |
DB.645 |
1.2332908 |
3.0053678 |
3.7049248 |
Perumnas |
L2 |
|
90 |
DB.124 |
1.3398308 |
2.9987333 |
4.0159532 |
Perumnas |
L3 |
|
93 |
DB.408 |
1.3396307 |
2.9994045 |
4.0162522 |
Perumnas |
L3 |
Tabel 3 Indeks keandalan sistem pada GI. Padang Sambian
|
SAIFI |
SAIDI |
CAIDI |
ASAI |
ASUI( × 10 -4) |
|
1.889752832061 |
5.702071455036 |
3.017363624647 |
0.9993490786010 |
6.50921398976 |
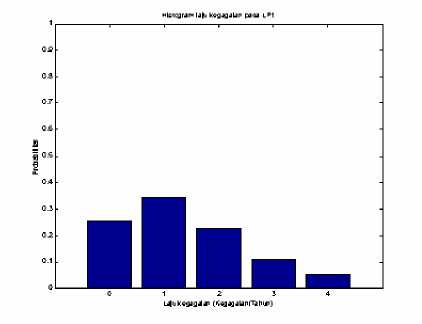
Gambar 2 Histogram laju kegagalan pada gardu DB.225

Gambar 5 Histogram lama padam pada gardu DB.304
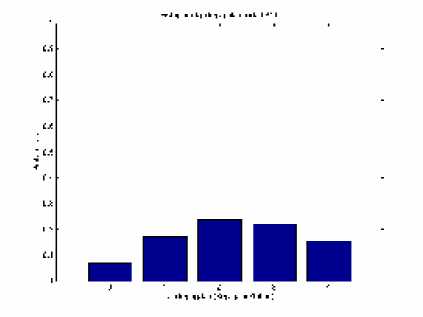
Gambar 3 Histogram laju kegagalan pada gardu DB.304
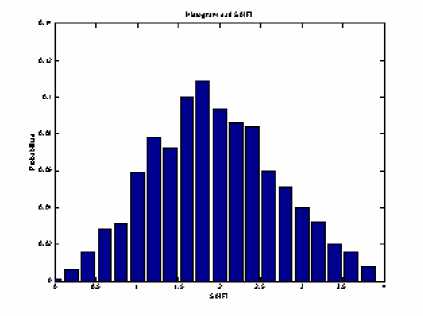
Gambar 6 Histogram dari SAIFI
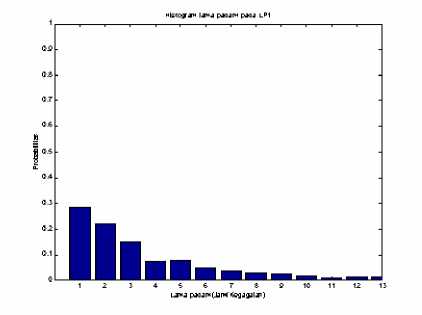
Gambar 4 Histogram lama padam pada gardu DB.225
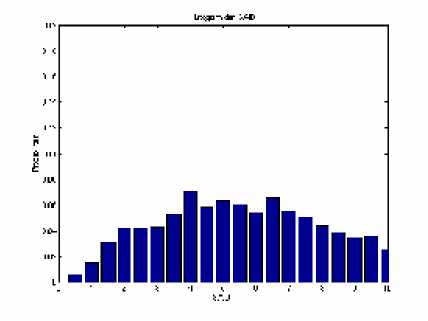
Gambar 7 Histogram dari SAIDI
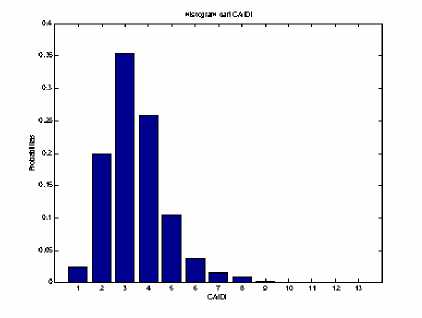
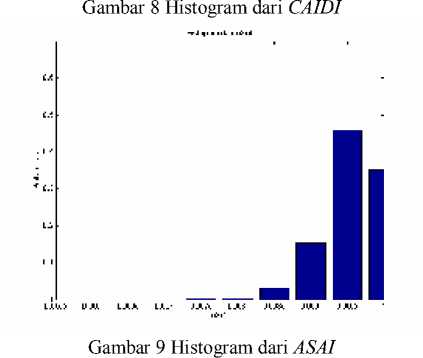
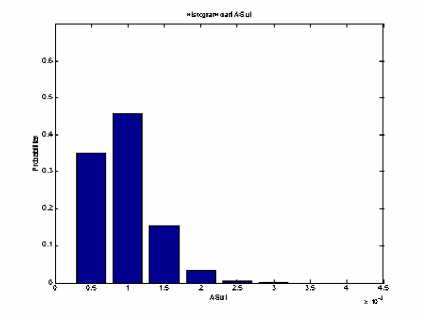
Gambar 10 Histogram dari ASUI
Berdasarkan hasil simulasi diatas dapat disimpulkan antara lain:
-
1. Indeks jangka waktu kegagalan (r) nilainya hampir sama yaitu 3,0 jam/kegagalan sedangkan Indeks frekwensi kegagalan (λ) dan indeks ketidaktersediaan (U) nilainya berbeda
tergantung panjang saluran.
-
2. Besarnya SAIFI = 1.88975, SAIDI = 5.702071, CAIDI = 3.01736, ASAI = 0.99935 dan ASUI = 0,00065.
-
3. Histogram probabilitas kegagalan umumnya mengacu pada dua pola yaitu: Pola I
menunjukkan bahwa laju kegagalan berada diatas dua kali per tahun sedangkan pola II menunjukkan laju kegagalan berada dibawah dua kali per tahun. Histogram probabilitas lama padam membentuk satu pola dimana lama padam 1 jam peluangnya paling besar.
-
4. Probabilitas distribusi keandalan sistem pada Gardu Induk Padangsambian menunjukkan indeks sistem yang berbeda setiap tahunnya yang dibedakan oleh peluang dari indeks itu sendiri.
-
5. DAFTAR PUSTAKA
-
[1] Billinton, R., Goel, R. 1986. An Analytical Approach to Evaluate Probability
Distribution Associated with the Reliability Indices of Electrical Distribution Systems, IEEE Trans. on Power Delivery, PWRD-I No. 3 pp. 245-251
-
[2] Billinton, R., Wang, P. 1999. Teaching distribution system reliability evaluation using monte carlo simulation. IEEE Transactions on Power Systems, vol. 14, no. 2, pp. 397–403.
-
[3] Billinton, R., Allan, Ronald N. 1996. Reliability Evaluation of Power Systems. 2nd ed. New York: Plenum Press.
-
[4] Billinton, R., Billinton, J. E. 1989. Distribution system reliability indices. IEEE Trans. Power Delivery, vol. 4, pp. 561-586.
-
[5] Bong, Duane. 2004. Monte Carlo Simulation. United States : http /www. Visionengineer. com/ Vision Engineer - Monte Carlo Simulation.htm
-
[6] Drakos, Nikos. 1994. Introduction to Monte Carlo Methods. United States : Computer Based Learning Unit University of Leeds.
-
[7] Ebeling, Charles E. 1997. An Introduction To Reliability and Maintainability
Engineering. Singapura : The McGraw-Hill Companies,Inc
-
[8] King. E.W., Canizares.C.A., Salama.M.M.A., 2004. Reliability Effects of Intentional Islanding on Backup Distributed
Generation Systems. Canada : Department of Electrical and Computer Engineering
University of Waterloo.
-
[9] PT. PLN (Persero) Distribusi Bali Area Pengatur Distribusi Bali. 2003. Standard Operation Procedure Distribusi 20 kV GI. Padangsambian. Denpasar : PT. PLN (Persero).
-
[10] PT. PLN (Persero). 1985. SPLN 59: Keandalan Pada Sistem Distribusi 20 kV dan 6 kV. Jakarta : Departemen Pertambangan dan Energi Perusahaan Umum Listrik Negara.
Teknologi Elektro
16
Vol. 4 No. 2 Juli – Desember 2005
PDF created with pdfFactory Pro trial version www.pdffactory.com
Discussion and feedback