ALOKASI PEMBEBANAN OPTIMAL PADA SISTEM PEMBANGKITAN DI BALI

Alokasi Pembebanan Optimal …

Wijaya

ALOKASI PEMBEBANAN OPTIMAL PADA

SISTEM PEMBANGKITAN DI BALI

I Ketut Wijaya

Teknik Elektro Fakultas Teknik Universitas Udayana

ABSTRAK

Pada sistem pengoperasian tenaga listrik, komponen biaya operasi terbesar adalah biaya bahan bakar. Oleh karenanya efisien pemakaian bahan bakar sangat besar pengaruhnya terhadap penghematan biaya operasi. Pengalokasian pembebanan pembangkit yang optimal merupakan suatu usaha untuk meminimumkan biaya operasi pada sistem tenaga listrik, tanpa melanggar persyaratan operasi.

Dalam penelitian ini, untuk menghitung alokasi pembebanan unit-unit pembangkit yang beroperasi digunakan algoritma optimasi yaitu; Gradient Projection Method (GPM).Dengan menggunakan metode ini untuk Sistem Pembangkitan Bali pada tanggal 31 Desember 2003, selama lima jam diperoleh penurunan biaya bahan bakar yang cukup signifikan.

• 1.    PENDAHULUAN

Tidak dapat dibantah bahwa listrik adalah bentuk energi yang saat ini merupakan penyokong kehidupan masyarakat yang sangat berarti. Begitu besarnya peranannya maka konsekuensinya dituntut ketersediaan, kesinambungan, dampak lingkungan yang bersih, kuantitas, dan kualitas yang tinggi, serta harga yang wajar.

Dalam perencanaan, pengoperasian, dan pengendalian sistem tenaga listrik muncul berbagai persoalan teknis maupun ekonomis, salah satunya diakibatkan oleh beban sistem yang dinamis. Di sisi lain energi listrik tidak dapat disimpan dalam jumlah banyak sehingga harus disediakan pada saat dibutuhkan oleh konsumen, akibatnya timbul persoalan dalam menghadapi kebutuhan daya listrik yang berubah dari waktu ke waktu.

Apabila daya yang dikirim dari bus bus pembangkit lebih besar dari kebutuhan daya pada bus bus beban, maka akan timbul pemborosan daya. Sedangkan apabila daya yang dibangkitkan lebih rendah dari kebutuhan maka akan timbul pemadaman lokal pada bus bus beban, yang akan mengakibatkan kerugian pada konsumen.

Pada sistem pengoperasian tenaga listrik, komponen biaya operasi terbesar adalah biaya bahan bakar. Penghematan biaya bahan bakar dalam prosentase yang kecil akan memberi dampak yang besar dalam jumlah rupiah, mengingat besarnya jumlah biaya bahan bakar tersebut diatas. Oleh karenanya efisien pemakaian bahan bakar sangat besar pengaruhnya terhadap penghematan biaya operasi.

Bali sangat terkenal sabagai salah satu tujuan wisata dunia, sampai saat ini sebagian pasokan tenaga listriknya masih tergantung dari Jawa melalui sistem interkoneksi Jawa-Bali lewat kabel laut yang hanya bisa dipakai dengan kapasitar sebesar 2 x 110 MW. Pembangkit yang beroperasi di Bali saat ini ada 9 unit PLTD dengan daya terpasang sebesar 65,7 MW, dan 4

unit PLTG dengan daya terpasang sebesar 125,5 MW, yang berlokasi di Pesanggaran. Satu unit PLTG berlokasi di Gilimanuk dengan daya terpasang sebesar 145 MW, yang merupakan pembangkit terbesar di Bali. Sehingga daya terpasang total setelah ditambah pasokan dari Jawa sebesar 556,2 MW, namun daya mampu sebesar 450 MW, hal ini disebabkan oleh derating kemampuan unit pembangkit. Apabila terjadi pemeliharaan unit pembangkit terbesar di Bali (145 MW), atau terganggunya kabel laut maka sistem kelistrikan di Bali akan mengalami kekurangan pasokan daya, sehingga akan terjadi giliran pemadaman listrik.

Upaya penanggulangan kekurangan daya sistem kelistrikan Bali, yang sudah dilakukan adalah penghematan daya di sisi pemakai (demand side management) yaitu dengan memasyarakatkan lampu hemat energi, sedangkan dari sisi suplay yaitu menambah kapasitas pembangkitan. Disamping hal di atas penghematan biaya operasi terutama penghematan biaya bahan bakar sistem di Bali juga tidak kalah pentingnya untuk dilakukan. Salah satu bagian pengoperasian sistem tenaga listrik yang mengarah ke hal ini adalah pengalokasian pembebanan optimal pada pembangkit. Hal ini merupakan suatu sistem untuk meminimumkan biaya operasi pada sistem tenaga listrik dengan cara mengoptimalkan pengalokasian pembangkitan daya antara generator-generator yang beroperasi pada sistem Bali yang memenuhi persyaratan pengoperasian sistem tenaga listrik. Persyaratan tersebut terutama adalah daya yang dibangkitkan cukup untuk memasok beban dan rugi-rugi daya, tidak melanggar kendala sistem.

• 2.    ALOKASI PEMBEBANAN EKONOMIS

Dalam sistem tenaga listrik, ada beberapa macam pembangkit tenaga (power plant), yaitu pembangkit thermal, pembangkit hidro, pembangkit nuklir dsb. Salah satu karakteristik terpenting adalah

biaya operasi. Biaya operasi masing-masing pembangkit berbeda, tidak hanya antar pembangkit, melainkan juga tergantung pada besarnya daya yang dibangkitkan. Dilain pihak, sistem tenaga listrik mempunyai beberapa pembangkit dengan karakteristik berbeda-beda. Jadi, yang menjadi perhatian dalam hal ini adalah bagaimana menentukan jumlah daya yang harus dibangkitkan oleh masing-masing pembangkit dalam suatu sistem tenaga listrik sehingga dapat memenuhi jumlah kebutuhan beban dengan biaya minimum , yang biasa duisebut alokasi pembebanan ekonomis (Economic Load Dispatch).

Masalah alokasi pembebanan ekonomis dirumuskan untuk memperoleh kodisi optimal pembangkit dengan meminimalkan total biaya bahan bakar, yang dinyatakan sebagai [6,12,17]:

N₂

Biaya _ operasi = ∑1∖aι + bi PGi + ci PGi )Rp/jam (1)

Kendala termasuk keseimbangan daya antara pembangkit dengan permintaan dan rugi-rugi daya :

N

^pD + ^pl = ∑ ^pg₁       (2)

i=1

Penjadualan daya aktif disyaratkan untuk memenuhi batas atas dan batas bawah pembangkit.

PGimin ≤ PGi ≤ PGimax     (3)

dengan

P_D : adalah total permintaan (MW), dan

P_L : adalah total rugi-rugi daya (MW)

P_Gi : adalah daya yang dibangkitkan oleh pembangkit ke-i (MW)

a_i ,b_i ,c_i : Konstanta-konstanta pembangkit

P_Gimin : pembangkitan minimal unit i (MW)

P_{Gi max} : pembangkitan maksimal unit i (MW)

N : Jumlah unit pembangkit berputar

Beberapa metode yang telah berhasil digunakan untuk memecahkan permasalahan ini, baik metode konvensional dan kecerdasan buatan (artificial intelligent). Metode konvensional yang sudah dikenal antara lain metode Lagrange (Lagrangian Relaxation method), metode interior point, metode Generalize Reduce Gradient (GRG method), dsb.

• 3.    METODE OPTIMISASI GRADIENT
  
  PROJECTION (GPM)

Metode proyeksi gradien (Gradient Projection Method / GPM) yang pertama kali diperkenalkan oleh Rosen (1960), adalah prosedur iterasi numeris untuk memperoleh nilai minimum (atau maksimum) dari suatu fungsi dengan kendala, telah terbukti mempunyai

banyak keuntungan dibandingkan dengan metode konvensional yang lain. Metode ini menghindari penggunaan fungsi penalti dan atau perhitungan dengan pengali Lagrange (Lagrange Multiplier ) [12,18]. Dan juga, panjang langkah (step length) dapat dihitung tanpa diperlukan algoritma search linier (linear-search algorithm) seperti pada metode yang lain. Selain itu, metode ini dapat menyelesaikan masalah alokasi pembebanan dalam waktu yang lebih cepat menuju konvergen dari pada metode yang lain [12, 18].

Permasalahan yang dapat dipecahkan dengan GPM dapat direpresentasikan sebagai berikut [4,6]:

P:      min z = f(x) (4)

Harus memenuhi kendala

Ax ≤ b       kendala ketidaksamaan

~~

Ax = b      kendala kesamaan

n

x ∈ IR

dimana,

f : fungsi nonlinier konvek

• A: Matriks dimensional [m x n]

• b: Matriks dimensional [m x 1]

~

A Matriks dimensional [r x n]

~

b Matriks dimensional [r x 1]

Untuk memecahkan masalah di atas maka pertamakali perlu dilakukan pelinieran (liniearizing) fungsi nonlinier f(x), menjadi Vf (x) . Dari kendala-kendala pada permasalahan (28) dapat dilihat jika m = 0, maka tidak ada kendala ketidaksamaan, dan bila r = 0, maka tidak ada kendala kesamaan.

Asumsikan bahwa x^k adalah nilai yang memungkinkan dan dapat dikerjakan dengan mudah (feasible point), dimana k = iterasi ke-n. Jika kk

Vf(x ) = 0, maka hal ini menunjukkan bahwa nilai xk

k

telah optimal. Sedangkan jika Vf (x ) ≠ 0, maka arah pencarian nilai x pada iterasi berikutnya adalah k

-Vf(x ), dalam arah pencarian ini menunjukkan bahwa fungsi f(x) diminimasikan berdasarkan kendala-kendala yang ada.

Sehingga prinsip dasar dari GPM adalah pencarian nilai optimum yang bergerak sepanjang gradient negatif dengan berdasarkan pada feasible direction. Langkah proyeksi dilakukan dengan sebelumnya mengalikan -Vf (x) dengan matriks

~~

proyeksi (projection matrix) P yang sesuai. Matriks P disebut projection matrix bila,

T ~  ~    ~~ ~

P = P dan P P =P (5)

Misalnya :

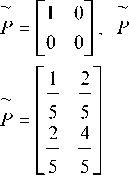
juga

T

1

0

OJ

merupakan

Langkah 1:

Mulai dengan nilai awal x¹ (dapat ditemukan dengan metode lain misalnya dengan metode 1 phase atau 2 phase), dan iterasi akan dimulai atau k:=1.

Langkah 2:

contoh

	A	dan b =	^b=^
Sediakan matriks A =	_ A <_		_b<_	hingga

A⁼x^k = b⁼ dan

A^<x^k < b^<

A

projection matrix

Untuk memperlihatkan cara kerja dari pendekatan GPM secara matematika, direpresentasikan permasalahan nonlinier sebagai berikut :

P:      min z = f(x) (6)

tunduk pada Ax ≤ b kendala pertidaksamaan

M =

dan

A

~~ n

Ax = b kendala persamaan x ∈ IR selanjutnya asumsikan kendala sebagai:

A=x^k = b=

I, jika M kosong

T ,      T ,-1

I - M (MM ) M, selainnya

~

Dengan P adalah matriks proyeksi.

A<x^k < b<      (7)

~~

Ax^k = b

bentuk matriks baru dengan

A =

A

A <

dan b =

b=

b<

(8)

setelah mengatur baris-baris dari matriks, bila diperlukan. Selanjutnya bentuk matriks baru

M =

A

~

A

(9)

dan definisikan projection matrix sebagai :

T ,..„T I

P = I - M (MM ) M , bila M bukan merupakan matriks kosong (10) ~

P = I, bila M adalah matriks kosong (11) Dengan I adalah matriks identitas.

Sebelum melakukan iterasi untuk mendapatkan nilai x yang optimal terlebih dahulu perlu dilakukan pelinieran (liniearizing) terhadap fungsi nonlinier f(x) menjadi fungsi obyektif yang linier Vf (x) . Algoritma GPM yang digunakan untuk memecahkan fungsi obyektif tersebut dapat ditulis sebagai berikut :

Langkah 0:

Abaikan fungsi kendala, cari nilai minimum dari fungsi obyektif tanpa fungsi kendala (dapat dilakukan dengan cara yang mudah mis: eleminasi), apakah nilai ini telah memenuhi syarat atau memungkinkan (feasible point) ? Jika Ya : Selesai, nilai optimal dari fungsi obyektif dengan kendala telah ditemukan. Jika Tidak : Lanjutkan ke langkah 1.

Langkah 3:

~

s^k =- P Vf(x^k),apakahs^k = 0?

Jika Ya : Lanjutkan ke langkah 4.

Jika Tidak : Lanjutkan ke langkah 7.

Langkah 4:

Apakah M matriks kosong?

Jika Ya : Selesai; x^k adalah solusi optimal dari fungsi obyektif dan fungsi kendalanya. Jika Tidak : Lanjutkan ke langkah 5.

Langkah 5:

u^k (M) =

u^k(A )

~ u^k(A)

=

, apakah u (A ) ≥ 0 ?

-(MM) ¹MVf (xk),

Jika Ya : Selesai, x^k adalah solusi optimal dari fungsi obyektif dan fungsi kendalanya. Jika Tidak : Lanjutkan ke langkah 6.

Langkah 6:

Pilih beberapa komponen negatif dari vektor u^k(A=) dan hapus baris yang sama (berhubungan) pada A⁼ , Lanjutkan ke langkah 2.

Langkah 7:

b* := b<-A<x^k,s* := A<s^kdan

1 *

λ : = ^<

min

* b_j

*^, s_j

s_j

*

> 0

. *     „

", jika s ≤ 0

+ x selainnya

^j

dan selesaikan minimasi 1 dimensi di bawah ini

P^λ := min f (xk + λsk) λ

*

s.t. 0 ≤ λ ≤ λ

Menunjukkan bahwa solusi optimal dari P^λ oleh λ^k, maka x^k+1 : = x^k + λ^ks^k, k:=i+1, dan kembali ke langkah 2.

Pada langkah ketiga Rosen telah memberikan sebuah metode rekursif untuk memperbaharui matriks proyeksi P yang diharapkan dapat mengurangi proses perhitungan. Dari algoritma di atas dapat disimpulkan bahwa iterasi GPM akan berakhir bila fungsi obyektif -k

P Vf(x ) = 0 (langkah 3), dan syarat fungsi kendala telah terpenuhi (langkah 4 dan 5).

• 4.    HASIL SIMULASI

Data awal yang berupa hasil pengukuran dan perhitungan yang diperoleh dari performance test ( komisioning terakhir yang dilakukan oleh PT. Indonesia Power - UPB Bali, data dalam lampiran 3). Data awal ini diolah menjadi karakteristik

pembangkit dengan teknik algoritma estimasi kuadrat terkecil (least-square method), sesuai dengan masukan program optimisasi (data dalam lampiran 4). Data yang diinputkan dalam program optimisasi adalah: persamaan karakteristik input-output setiap unit-unit pembangkit, kapasitas daya maksimum dan minimum setiap unit dan beban harian.

Penjadwalan Tanpa Menggunakan Teknik Optimisasi

Untuk simulasi beban digunakan sampel data penjadwalan pembebanan pembangkit pada tanggal 31 Desember 2003 ( Lampiran ). Penjadwalan yang dipakai perbandingan adalah mulai dari pukul 18.00 - 22.00 atau 5 jam periode pembebanan.

Dari data laporan operasi tanggal 31 Desember 2003 didapatkan beban-beban yang harus disuplai oleh unit-unit pembangkit Sistem PT. Indonesia Power UBP-Bali. Selama 5 jam operasi tersebut, 9 unit PLTD dan 4 unit PLTG dioperasikan.

Tabel 1. Data pembebanan PT. Indonesia Power UBP. Bali tanggal 31 Desember 2003

Unit	Batas Pembangkitan		Pukul
	Pmin	Pmak	18.00	19.00	20.00	21.00	22.00
PLTD-2 (MW)	1,27	4,6	4,60	4,60	4,60	4,60	4,60
PLTD-4 (MW)	1,27	4,5	4,30	4,30	4,30	4,30	4,30
PLTD-5 (MW)	1,05	3,5	3,20	3,20	3,20	3,20	3,20
PLTD-6 (MW)	1,70	5,3	5,30	5,30	5,30	5,30	5,30
PLTD-7 (MW)	1,70	5,6	5,30	5,30	5,30	5,30	5,30
PLTD-8 (MW)	1,60	4,5	4,30	4,50	4,50	4,50	4,50
PLTD-9 (MW)	1,60	4,5	2,10	2,50	2,50	2,50	2,50
PLTD-10 (MW)	3,00	10,5	9,20	9,50	9,50	9,50	9,50
PLTD-11 (MW)	3,80	10,5	7,00	7,50	7,50	7,50	7,00
PLTG-1 (MW)	5,00	19,4	16,70	16,70	16,70	15,90	15,80
PLTG-2 (MW)	5,00	19,8	18,70	18,90	18,80	18,90	18,90
PLTG-3 (MW)	10,00	39,5	33,00	37,00	37,00	37,00	37,00
PLTG-4 (MW)	10,50	35	33,00	35,00	35,00	35,00	35,00
TOTAL (MW)			146,70	154,30	154,20	153,50	152,90
Data beban (MW)			146,70	154,30	154,20	153,50	152,90

Sumber: Laporan Pengusahaan PT. Indonesia Power UBP Bali

Pembebanan pada masing-masing pembangkit disubstitusikan dalam persamaan karakteristik masing-masing sehingga akan diperoleh biaya bahan bakar selama periode lima jam yang besarnya Rp. 448.944.423,460

algoritma Gradient Projection Method (GPM), untuk menentukan penjadwalan ulang pembebanan masing-masing unit pembangkit. Hasil simulasi dari ketiga algoritma seperti tabel 3. berikut:

Penjadwalan Menggunakan Teknik Optimisasi

Data beban selama lima jam ( 18.00 – 22.00), dipakai dalam optimisasi dengan menggunakan

Tabel 3. Hasil simulasi pembebanan masing-masing unit pembangkit selama lima jam.

Unit	Batas Pembangkitan		Pukul
	P . min	Pmak	18.00	19.00	20.00	21.00	22.00
PLTD-2	1,27	4,6	3.662	4.600	4.600	4.600	4.600
PLTD-4	1,27	4,5	3.123	3.722	3.713	3.650	3.596
PLTD-5	1,05	3,5	3.500	3.500	3.500	3.500	3.500
PLTD-6	1,7	5,3	3.500	5.300	5.300	5.300	5.300
PLTD-7	1,7	5,6	5.600	5.600	5.600	5.600	5.600
PLTD-8	1,6	4,5	4.500	4.500	4.500	4.500	4.500
PLTD-9	1,6	4,5	4.500	4.500	4.500	4.500	4.500
PLTD-10	3	10,5	10.500	10.500	10.500	10.500	10.500
PLTD-11	3,8	10,5	10.500	10.500	10.500	10.500	10.500
PLTG-1	5	19,4	19.400	19.400	19.400	19.400	19.400
PLTG-2	5	19,8	7.471	9.370	9.341	9.142	8.971
PLTG-3	10	39,5	39.500	39.500	39.500	39.500	39.500
PLTG-4	10,5	35	29.145	33.308	33.246	32.808	32.433
TOTAL	47.49	167.2	146,7	154,3	154,2	153,5	152,9
Beban			146,7	154,3	154,2	153,5	152,9

Pembebanan masing masing pembangkit semuanya dalam batas-batas pembangkitan maksimum dan minimum.

• 5.    PEMBAHASAN

Perbandingan total biaya bahan bakar untuk pengalokasian pembebanan masing-masing unit pembangkit dengan algoritma GPM dengan data pembebanan lapangan ditabelkan dalam tabel 4. Dari hasil simulasi, didapatkan bahwa total biaya yang dihitung dari pembebanan hasil optimisasi lebih rendah dari total biaya yang dihitung dari data lapangan. Prosentase penurunanya adalah: sebesar Rp.17.767.483,98 (3,96%).

Tabel 4 : Perbandingan biaya

JAM KE	Biaya bahan bakar
	Lapangan ( Rp )	Simulasi ( Rp )
1	87.166.372,41	83.220.203,66
2	90.610.565,45	87.310.150,71
3	90.530.308,31	87.253.956,69
4	90.412.619,69	86.862.621,23
5	90.224.557,60	86.530.008,13
TOTAL	448.944.423,46	431.176.940,43

Dengan menggunakan teknik optimisasi pada

Sistem Bali selam lima jam (18.00 – 22.00) pada

tanggal 31 Desember 2003 diperoleh penurunan biaya bahan bakar yang cukup signifikan.

• 6.    KESIMPULAN

Dengan menggunakan metode optimisasi GPM untuk sistem pembangkitan bali pada tanggal 31 Desember 2003, selama lima jam dari jam 18.00 sampai 22.00 diperoleh penurunan biaya bahan bakar yang cukup signifikan. Sehingga dapat disimpulkan bahwa metode ini dapat dipergunakan untuk melakukan perhitungan alokasi pembebaban pembangkit pada sistem pembangkitan Bali.

• 7.    DAFTAR PUSTAKA

• [1]    David A. Wismer, and R. Chattergy, Introduction to Nonlinear Optimization, A problem solving approach, Nort-Holland Publishing Company, New York, 1978.

• [2]    El-Hawary, M E. 1983. Electrical Power System Design & Analysis. Restu Publishing Company: New Dehli

• [3]    Eiselt H. A.. 1987. Continous Optimization Models. Walter de Gruyter: New York.

• [4]    Grainger, J J and Stevenson, W D. Jr. 1994. Power System Analysis. Tata-McGraw-Hill: New Dehli.

• [5]    James A. Momoh. 1994. The Quadratic Interior Point Method Solving Power System Optimization Problems : IEEE Transaction on Power System, Vol. 9, No. 3. USA : IEEE Power Engineering Society.

• [6]    Kirchmayer, L K. 1958. Economic Operation of Power System. John Wiley and Sons Inc: New York.

• [7]    Lee, K. Y., J. L. Ortiz, Fuel-cost minimization for both real-and reactive power dispatches, IEEE Proceedings, Vol. 131, Pt. C, No. 3, May 1984?

• [8]    Marsudi, D. 1990. Operasi Sistem Tenaga Listrik. Jakarta : Balai Penerbit & Human ISTN: Jakarta.

• [9]    Najamudin, H. 1995. Economic Load Dispatch Optimising Real and Reactive Power. Energi & Listrik : Jakarta.

• [10]    Rosen, J.B., The Gradient Projection method for non-linear programming-Part I ‘Linear constraints, J. Soc. Indust. Appl. Math., 1960,3,pp. 181-217.

• [11]    Saadat, H. 1999. Power System Analysis. Tata-McGraw-Hill: New Dehli.

• [12]    Shu-Cherng Fang. 1993. Linear Optimization And Extensions: Theory and Algorithms. Prentice-Hall International, Inc. New Jersey.

• [13]    Sukerayasa, I Wayan. 2000. Penjadwalan Unitunit Hidrotermal Studi Kasus PT. PLN (PERSERO) Area-3. Yogyakarta.

• [14]    Wood Allen, J. and Bruce F. Woollenberg. 1984.

Power Generation Operation and Control. John Wiley & Sons : Singapore.

Teknologi Elektro

42

Vol.3 No.2 Juli – Desember 2004