Perbandingan Metode Extreme Learning Machine dan Particle Swarm Optimization Extreme Learning Machine untuk Peramalan Jumlah Penjualan Barang
on
84
Teknologi Elektro, Vol.15, No.1, Januari - Juni 2016
Perbandingan Metode Extreme Learning Machine dan Particle Swarm Optimization Extreme Learning Machine untuk Peramalan Jumlah Penjualan Barang
I Putu Susila Handika1, Ida Ayu Giriantari2,Agus Dharma3
Abstract— Extreme Learning Machine (ELM) merupakan salah satu metode pembelajaran dari Artificial Neural Network yang memberikan tingkat akurasi dan kecepatan yang lebih baik dari pada metode pembelajaran lainnya. Salah satu kelemahan dari metode ELM adalah jumlah hidden nodes ditentukan dengan cara try and error, sehingga tidak bisa diketahui berapa jumlah hidden nodes yang tepat untuk mendapatkan hasil peramalan menggunakan metode ELM. Untuk mengatasi masalah tersebut digunakan metode optimasi Particle Swarm Optimization untuk mencari jumlah hidden nodes yang optimal. Data yang digunakan untuk keperluan analisis adalah data time series penjualan barang salah satu minimarket di Bali. Hasil peramalan akan diukur mengunggunakan Mean Square Error (MSE) dengan data uji yang sama. Hasil penelitian menunjukkan metode PSO dapat diterapkan pada metode ELM untuk mengoptimasi jumlah hidden nodes. MSE yang dihasilkan oleh metode PSO ELM lebih kecil dibanding metode ELM. Selain itu range error yang dihasilkan oleh metode PSO ELM juga lebih kecil dibanding metode ELM.
Kata Kunci— Peramalan; Extreme Learning Machine; Particle Swarm Optimization, Mean Square Error.
-
I. PENDAHULUAN
Kemunculan minimarket yang begitu banyak membuat manajemen perusahaan harus berfikir kreatif agar dapat bersaing dengan usaha sejenis dalam merebut pangsa pasar. Salah satu cara untuk merebut pangsa pasar adalah dengan menyediakan barang yang diperlukan oleh konsumen. Pengelolaan sebuah minimarket diperlukan untuk menjaga persediaan barang-barang tetap tersedia karena persediaan barang merupakan bagian yang sangat penting dalam perkembangan sebuah minimarket. Jumlah persediaan sangat erat kaitannya dengan berapa target penjualan pada setiap barang yang dijual. Dapat dibayangkan, apabila pemilik tidak mengetahui kapan ia harus memesan barang atau bahkan tidak tahu berapa barang yang harus dipesan agar dapat menjaga jumlah persediaan di minimarket. Pemilik minimarket bisa saja memesan banyak barang untuk disimpan pada minimarketnya, namun yang perlu diperhatikan adalah jika barang dan penjualan yang terjadi sedikit, maka barang yang tersimpan pada minimarket dapat menyebabkan kerugian
terhadap pemilik minimarket. Pengelola minimarket harus dapat mengetahui berapa jumlah minimal dan maksimal barang agar persediaan barang di minimarket menjadi optimal. Jumlah minimal dan jumlah maksimal barang ditentukan dengan mengetahui berapa jumlah penjualan periode selanjutnya.
Pengelolaan barang yang terdapat pada minimarket saat ini telah menggunakan sistem yang dapat mengatur jumlah minimum dan maksimum barang untuk setiap minimarket. Metode peramalan yang digunakan dalam menentukan jumlah penjualan barang periode selanjutnya untuk setiap minimarket adalah moving average. Hasil peramalan yang didapat dari metode tersebut tidak dapat terjamin karena pola data yang terdapat pada bidang retail adalah pola data non stasioner. Suatu metode dibutuhkan untuk dapat meramalkan perilaku data non stasioner agar dapat mengurangi kesalahan yang terjadi. Metode Artificial Neural Network (ANN) dapat digunakan untuk mengatasi masalah perilaku data non satsioner karena metode ANN memiliki kemampuan untuk belajar [1]. Salah satu metode pembelajaran pada ANN adalah Extreme Learning Machine (ELM) yang memberikan tingkat akurasi dan kecepatan yang lebih baik dari pada metode pembelajaran lainnya [2]. Salah satu kelemahan dari metode ANN adalah penentuan parameter hidden nodes secara manual. Untuk mendapatkan hasil yang optimal metode ANN dapat digabungkan dengan salah satu metode optimasi yaitu Particle Swarm Optimization (PSO). Penggabungan metode PSO dan ANN dapat memberikan hasil yang lebih akurat dibanding metode ANN [3].
Pada penelitian ini, metode PSO akan digabungkan dengan metode ELM untuk meramalkan total penjualan barang pada minimarket. Penggabungan metode PSO dan ELM akan menghasilkan jumlah hidden nodes yang optimal sehingga didapatkan hasil peramalan yang lebih akurat.
Extreme Learning Machine (ELM) adalah sebuah metode pembelajaran yang baru dari ANN yang menggunakan arsitektur single hidden layer feedforward. Pembuatan metode ini bertujuan untuk mengatasi permasalahan dari metode ANN terutama dalam hal learning speed. Parameter-parameter pada metode ELM seperti input weight dan hidden bias dipilih secara random, sehingga ELM memiliki learning speed yang cepa. Berbeda dari ANN Feedforward, metode ELM memiliki model matematis yang lebih sederhana dan efektif.
Xi = [Xu, Xi2,-, XiN]τ∈Rn (1)
Xt = [xtl’ Xt2, ■”, xtN]T ∈ Rn (2)
Secara umum fungsi matematis untuk Single Hidden
Teknologi Elektro, Vol.15, No.1, Januari - Juni 2016
Layer Feedforward Neural Networks (SLFNs) dengan jumlah hidden nodes sebanyak N dan activation function (x) ditunjukkan pada Persamaan 3 [2].
∑hβlgl(χj) = ∑t1βigi(wixj + bl) = oj (3)
Keterangan :
j adalah bilangan 1, 2, ..., N
wi = (wi1, wi2, ..., win)T adalah vektor dari weight yang menghubungkan i th hidden nodes dan input nodes.
βt = (βi1, βi2’■■■’ βtn)τ adalah vektor bobot yang menghubungkan i th hidden dan output nodes.
bi adalah threshold dari i th hidden nodes.
WiXj adalah inner produk dari wi dan xj.
Arsitektur sederhana metode ELM ditunjukkan pada Gambar 1.
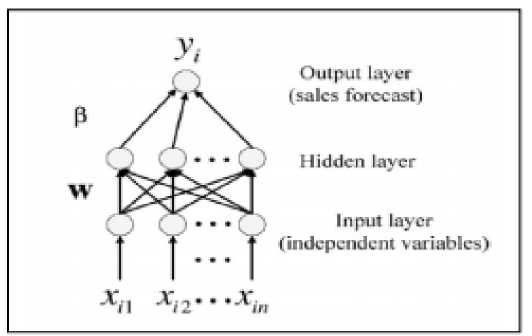
Gambar 1. Arsitektur ELM [2].
Langkah-langkah yang dilakukan untuk menghitung menggunakan metode ELM adalah sebagai berikut [4].
-
1) Langkah 1: Tentukan bobot dan nilai bias secara random.
-
2) Langkah 2: Hitung output pada hidden layer menggunakan Persamaan 4.
G(aι, x1, b1) = ∑^aixj + bi) (4)
-
3) Langkah 3: Hitung bobot akhir dari hidden layer menggunakan Persamaan 5.
β = H+ T (5)
H+ merupakan matriks Moore-Penrose Generalized Invers dari matriks H. Sedangkan matriks H merupakan matriks yang tersusun dari ouput masing-masing hidden layer. Sedangkan T merupakan matriks target.
-
4) Langkah 4: Menghitung semua keluaran di unit output dengan menggunakan Persamaan 6.
g(χ) = 1^
-
1 + e x
-
III. Particle Swarm Optimization (PSO)
Particle Swarm Optimization (PSO), merupakan sebuah metode optimasi yang didasarkan pada perilaku sebuah kawanan serangga misalnya semut, rayap, lebah atau burung. Suatu partikel dalam ruang memiliki posisi dan setiap posisi dalam ruang pencarian merupakan alternatif solusi yang dapat dievaluasi menggunakan fungsi objektif. Setiap partikel dapat menyesuaikan posisi dan kecepatan masing-masing dengan cara setiap partikel menyampaikan informasi terbaiknya kepada partikel yang lain [5]. Sebagai contoh perilaku yang diadopsi oleh metode ini adalah perilaku burung yang mempunyai keterbatasan dalam hal kecerdasan, namun burung-burung tersebut akan mengikuti kebiasaan (rule) seperti berikut [6].
-
1) Seekor burung tidak berada terlalu dekat dengan burung yang lain.
-
2) Burung tersebut akan mengarahkan terbangnya ke arah rata-rata keseluruhan burung.
-
3) Kawanan burung akan memposisikan diri dengan rata-rata posisi burung yang lain dengan menjaga sehingga jarak antar burung dalam kawanan itu tidak terlalu jauh.
Rumus untuk menghitung posisi dan kecepatan pada PSO ditunjukkan pada Persamaan 7 dan 8.
Xi (t)= xn(t), xι2{t},-, XiN W (7)
Vi (t) = V(t), Vi2 (t),-, ViN (t) (8)
Keterangan :
X adalah posisi partikel
V adalah kecepatan partikel
i adalah indeks partikel t adalah iterasi ke-t
N adalah ukuran dimensi ruang
Penggambaran status partikel pada PSO, digunakan persamaan 9 dan 10.
Vt = Vt(t - 1) + c1r1(xt - xSf - 1)) + c2r2 (xg - XSf - 1)) (9)
Xi (t) = V1 (t)+ Xi (t- 1) (10)
Keterangan :
Xt = xt1, xt∙2,-, x\N merepresentasikan local best dari partikel ke-i.
Susila Handika: Perbandingan Metode Extrame learning …
p-ISSN:1693 – 2951; e-ISSN: 2503-2372
Xg = xg, xg,..., x^ merepresentasikan global best dari seluruh kawanan.
c adalah konstanta yang bernilai positif yang biasanya disebut sebagai learning factor.
r adalah suatu bilangan random yang bernilai antara 0 - 1.
Langkah-langkah untuk menghitung menggunakan metode PSO adalah sebagai berikut.
-
1) Langkah 1: Inisialisasi posisi awal partikel secara random.
-
2) Langkah 2: Hitung nilai fitness terbaik dari setiap partikel.
-
3) Langkah 3: Tentukan nilai fitness terbaik, dan tetapkan sebagai Gbest.
-
4) Langkah 4: Hitung kecepatan setiap partikel menggunakan persamaan 9. Dan hitung posisi setiap partikel menggunakan persamaan 10.
-
5) Langkah 5: Evaluasi nilai fitness dari setiap partikel menggunakan posisi yang baru.
-
6) Langkah 6: Jika kondisi belum terpenuhi, maka ulangi ke langkah 4.
Untuk menghitung akurasi peramalan digunakan metode MSE (Mean Square Error) yang merupakan ukuran ketepatan sebuah metode peramalan. MSE merupakan rata-rata error kuadrat dari untuk setiap data. Rumus MSE dapat dilihat pada Persamaan 14 [7].
MSE = ^∑±- =
n
n
(11)
Keterangan :
E adalah Error peramalan.
n adalah Jumlah data.
Xi adalah Data nyata ke i.
Fi adalah Data hasil peramalan ke i.
Metode yang digunakan untuk meramalkan jumlah penjualan adalah PSO ELM. Metode PSO berfungsi untuk mencari jumlah hidden nodes yang optimal yang selanjutnya digunakan oleh metode ELM untuk mencari jumlah penjualan barang periode selanjutnya. Secara umum proses peramalan jumlah penjualan barang menggunakan metode PSO dan ELM ditunjukkan pada Gambar 2
Proses awal dari sistem ini adalah memasukkan inputan parameter yang diperlukan dalam proses perhitungan peramalan menggunakan metode PSO dan ELM yaitu makasimum iterasi dan jumlah partikel. Pada penelitian ini jumlah partikel yang digunakan adalah 20 sampai 30 partikel, karena penggunaan pada umumnya partikel yang digunakan berkisar pada angkat tersebut. Selain itu penggunaan partikel yang terlalu banyak akan menyebabkan proses perhitungan PSO menjadi panjang dan tidak stabil [6]. Sedangkan untuk jumlah iterasi yang digunakan .
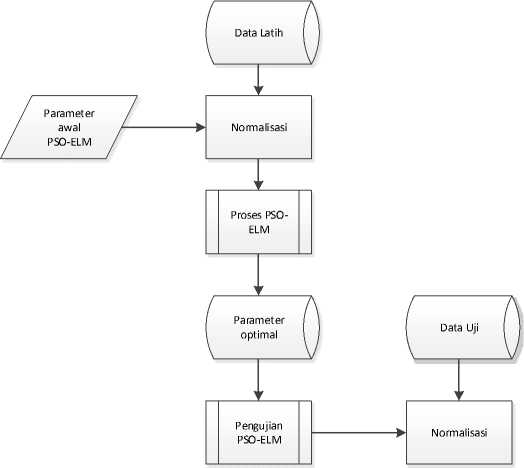
Gambar 2. Proses Peramalan Menggunakan Metode PSO ELM.
Selanjutnya sistem akan mengambil data dari database untuk dilakukan proses pelatihan. Data latih tersebut akan dinormalisasi agar mengurangi noise data serta mengurangi dominasi nilai yang bernilai besar terhadap variable yang bernilai kecil. Proses normalisasi yang digunakan adalah min max normalization. Proses selanjutnya adalah masuk ke subproses PSO ELM. Sub proses metode PSO ELM ditunjukkan pada Gambar 3. Pada sub proses PSO ELM, langkah awal yang dilakukan adalah membuat populasi untuk PSO secara random yang dalam kasus ini merupakan jumlah hidden nodes dari ELM. Setelah itu dilakukan proses inisialisasi bobot dan bias dimana bobot menggunakan nilai random. Selanjutnya dilakukan perhitungan output (dalam kasus ini adalah hasil peramalan penjualan barang) untuk setiap hidden nodes yang ditetapkan. Setelah didapatkan hasil output untuk setiap hidden nodes, selanjutnya adalah proses perhitungan vektor bobot output. Proses perhitungan output menggunakan fungsi aktivasi dilakukan setelah proses perhitungan vektor bobot output selesai. Hasil dari perhitungan menggunakan fungsi aktivasi ditetapkan sebagai Gbest dari populasi PSO, lalu merubah posisi global dan kecepatan setiap partikel PSO. Setelah itu dilakukan proses evaluasi nilai fitness menggunakan posisi yang baru. Jika kondisi yang diinginkan belum terpenuhi, proses akan kembali ke inisialisasi jumlah hidden nodes, bobot dan bias. Jika kondisi telah terpenuhi, proses dikatakan selesai dan posisi terbaik pada PSO akan menjadi jumlah hidden nodes optimal pada metode ELM
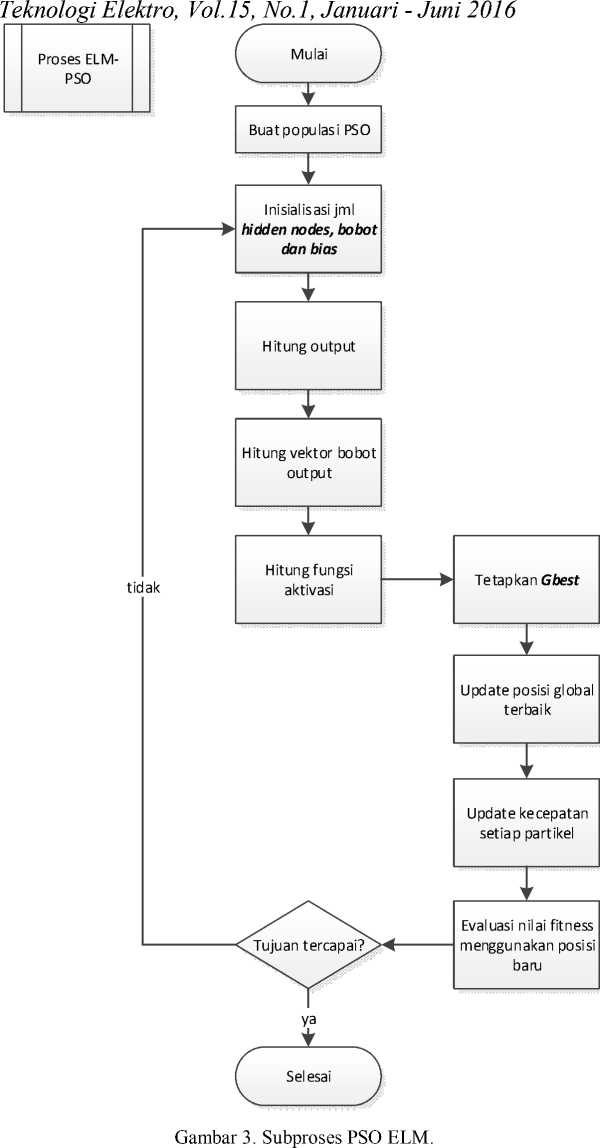
Setelah proses PSO ELM selesai dilakukan proses selanjutnya adalah proses pengujian untuk mencari akurasi dari metode peramalan. Proses pengujian pada penelitian ini adalah membandingkan hasil peramalan metode ELM yang dioptimasi menggunakan metode PSO dan ELM tanpa optimasi. Pada proses PSO, jumlah partikel yang yang digunakan pada umumnya adalah dari 20 sampai 30 partikel karena penggunaan banyak partikel akan membuat perhitungan menjadi panjang dan tidak stabil [6]. Sedangkan pada metode ELM jumlah hidden neurons yang digunakan adalah bilangan random antara 1 sampai dengan 100 karena jumlah hidden neurons yang optimal belum diketahui dan dalam penelitian yang dilakukan oleh Sheela dkk, jumlah hidden neurons yang didapat 1 - 101 [8]. Sub proses pengujian hasil peramalan PSO ELM dan ELM tanpa optimasi ditunjukkan pada Gambar 4.
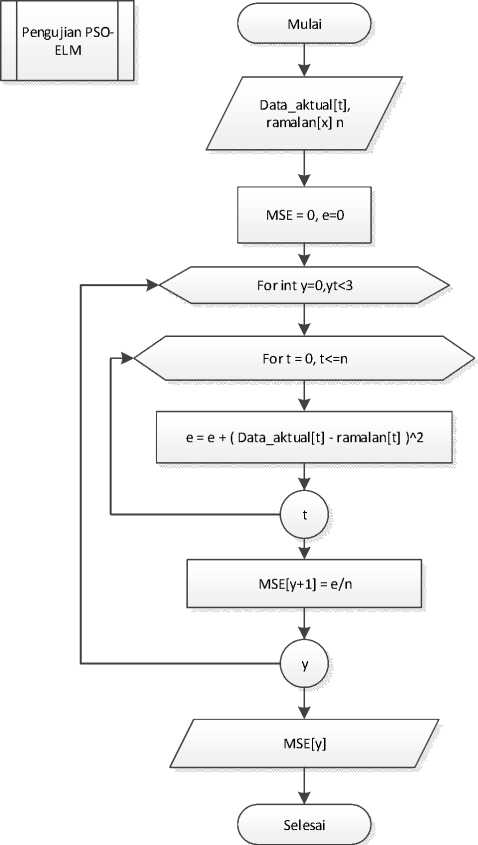
Gambar 4. Pengujian PSO ELM.
-
A. Aplikasi Peramalan
Gambar 5 menunjukkan hasil aplikasi peramalan yang telah dibuat menggunakan Matlab 2012. Data penjualan yang diproses disimpan dalam file excel kemudian dibaca oleh aplikasi peramalan. Jumlah partikel awal PSO ditentukan oleh user.
Susila Handika: Perbandingan Metode Extrame learning …
p-ISSN:1693 – 2951; e-ISSN: 2503-2372
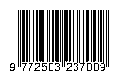
Gambar 5. Aplikasi Peramalan.
Output data disimpan dalam variable Matlab. Pada Gambar 6 dapat dilihat jumlah data yang terdapat pada data 1 adalah 771 record dimana 80% dari jumlah data tersebut digunakan untuk proses training dan 20% digunakan pada proses testing [9].
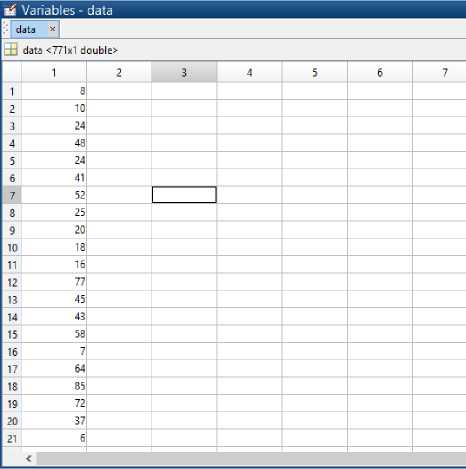
Gambar 6. Data peramalan pada matlab.
Proses training berfungsi untuk mencari jumlah hidden nodes optimal meggunakan metode PSO ELM. Jumlah hidden nodes tersebut akan digunakan pada proses testing. Pada Gambar 7 menunjukkan grafik akurasi yang dihasilkan pada setiap iterasi.
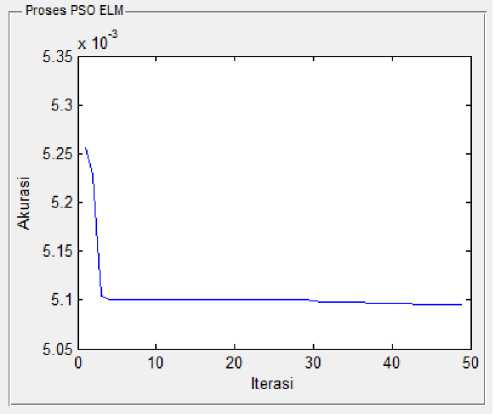
Gambar 7. Proses pencarian akurasi minimum PSO.
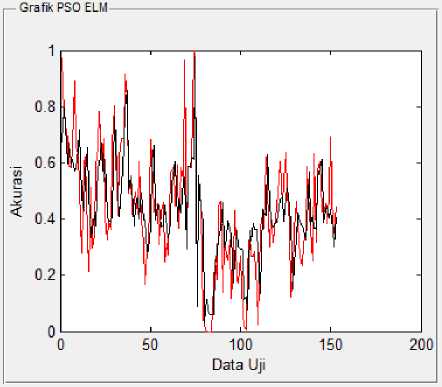
Gambar 8. Grafik hasil peramalan PSO ELM.
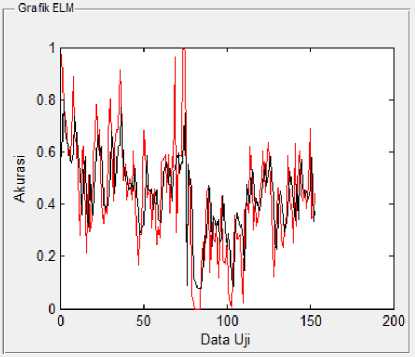
Gambar 9. Grafik hasil peramalan ELM.
Gambar 8 dan Gambar 9 menunjukkan bahwa hasil peramalan menggunakan metode ELM yang dioptimasi dengan metode PSO tidak jauh berbeda dengan hasil peramalan yang didapat menggunakan metode ELM tanpa optimasi. Gambar 10 juga menunjukkan hasil peramalan yang didapat tidak terlalu jauh yaitu sejumlah 74 untuk metode ELM yang dioptimasi dengan metode PSO dan sejumlah 69 untuk metode ELM tanpa optimasi. Hasil akurasi yang dihasilkan untuk metode ELM adalah 0,02421, sedangkan hasil yang didapat pada metode ELM tanpa optimasi adalah 0,01757. Dengan demikian metode PSO dapat digunakan untuk mengoptimasi jumlah hidden nodes dari metode ELM walaupun hasil yang didapat tidak terlalu signifikan. Waktu proses yang didapat oleh metode PSO ELM adalah 33,0944 detik sedangkan metode ELM meng-hasilkan waktu proses sebesar 0,0570. Jadi dalam hal waktu proses, metode ELM lebih cepat dibandingkan metode PSO ELM.
Setelah mendapatkan hasil akurasi minimum, maka dilanjutkan dengan proses peramalan menggunakan metode ELM menggunakan jumlah hidden nodes yang telah didapatkan pada proses training. Hasil perhitungan metode PSO ELM dan ELM digambarkan pada Gambar 8 dan Gambar 9.
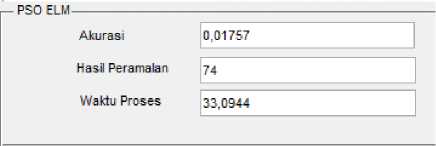
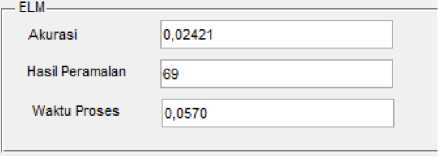
Gambar 10. Output Peramalan PSO ELM dan ELM.
-
B. Analisis Metode PSO ELM dan ELM
Hasil pengujian yang telah dilakukan pada bab VI didapat hasil perbandingan MSE antara metode PSO ELM dan ELM yang ditunjukkan pada TABEL 1.
TABEL 1. PERBANDINGAN MSE METODE PSO ELM DAN ELM
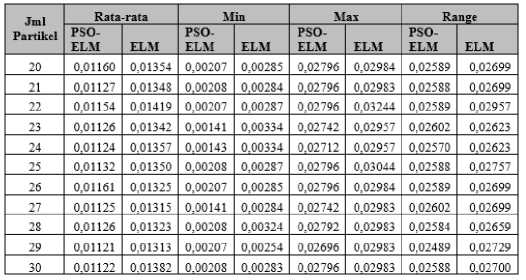
Pada TABEL 1 dapat dilihat rata-rata akurasi, nilai minimum dan nilai maximum yang dihasilkan oleh metode PSO ELM selalu lebih kecil dari pada metode ELM tanpa menggunakan optimasi. Hasil pada TABEL 1 menunjukkan rata-rata yang dihasilkan oleh metode PSO ELM berkisar antara 0,01121 sampai dengan 0,01161 sedangkan rata-rata yang dihasilkan oleh metode ELM berkisar antara 0,01315 sampai dengan 0,01419. Dengan demikian dapat dikatakan akurasi yang didapat oleh metode PSO ELM lebih kecil dibanding metode ELM. Selain itu range yang didapat dari metode PSO ELM lebih kecil dari metode ELM tanpa optimasi. Hal tersebut menunjukkan bahwa penggunaan metode optimasi PSO dapat memperkecil range kesalahan yang didapat dari metode ELM.
-
C. Waktu Proses Metode PSO ELM
Pengujian ini dilakukan menggunakan tiga spesifikasi komputer yang berbeda. Tujuan dari pengujian ini adalah mengetahui waktu proses dari metode PSO ELM. Spesifikasi perangkat pengujian yang digunakan ditunjukkan pada TABEL 2. Dan hasil pengujian menggunakan 10 item best seller di-tunjukkan pada
TABEL 3.
TABEL 2. SPESIFIKASI PERANGKAT PENGUJIAN
|
Speksifikasi No. |
Processor |
RAM |
|
Laptop |
Core i5 (4 Core) |
4 GB |
|
Server |
Intel Xeon E5 (24 Core) |
32 GB |
|
PC |
Dual Core (2 Core) |
2 GB |
TABEL 3. HASIL PENGUJIAN WAKTU PROSES METODE PSO ELM.
|
Pengujian |
Rata-rata PSO ELM Laptop (s) |
Rata-rata ELM Laptop (s) |
Rata-rata PSO ELM Server (s) |
Rata-rata ELM Server (s) |
Rata-rata PSO ELM PC (s) |
Rata-rata ELM PC (s) |
|
1 |
19,9726 |
0,0412 |
6,4314 |
0,0123 |
24,4167 |
0,1164 |
|
2 |
19,9726 |
0,0419 |
7,0168 |
0,0288 |
25,4780 |
0,1255 |
|
3 |
19,7941 |
0,0416 |
6,4440 |
0,0128 |
25,2081 |
0,1206 |
|
4 |
20,3800 |
0,0419 |
5,8912 |
0,0287 |
25,3318 |
0,0999 |
|
5 |
17,5409 |
0,0415 |
6,4578 |
0,0187 |
25,3082 |
0,0920 |
|
6 |
20,2524 |
0,0414 |
6,4263 |
0,0017 |
24,2056 |
0,1275 |
|
7 |
20,2405 |
0,0412 |
6,4312 |
0,0123 |
25,9315 |
0,1095 |
|
8 |
20,2959 |
0,0414 |
5,8967 |
0,0288 |
25,1250 |
0,1226 |
|
9 |
20,4715 |
0,0419 |
5,6763 |
0,0287 |
25,1010 |
0,1322 |
|
10 |
21,1135 |
0,0412 |
6,4552 |
0,0123 |
25,3237 |
0,1113 |
Jika dilihat pada
TABEL 3, waktu proses metode ELM lebih cepat dibandingkan dengan metode PSO ELM. Hal tersebut disebabkan oleh proses pencarian jumlah hidden nodes yang optimal pada metode PSO. Sehingga proses perhitungan akan menjadi lebih banyak dan waktu proses yang dibutuhkan akan menjadi lebih lama [10]. Selain itu penggunaan perangkat pengujian akan berpengaruh dengan waktu proses. Waktu proses tercepat dihasilkan oleh perangkat pengujian meng-gunakan server dan waktu proses terlama dihasilkan oleh perangkat pengujian menggunakan PC seperti yang di-tampilkan pada
TABEL 3.
Dari pembahasan pada bagian sebelumnya, Rata-rata Mean Square Error (MSE) yang dihasilkan oleh metode PSO ELM lebih kecil dibanding metode ELM, yaitu berkisar antara 0,01121 sampai dengan 0,01161 untuk metode PSO ELM dan berkisar antara 0,01315 sampai dengan 0,01419 untuk metode ELM. Dengan demikian dapat dikatakan metode PSO mampu mengoptimasi jumlah hidden nodes dari metode ELM untuk meramalkan jumlah penjualan barang. .
REFERENSI
-
[1] A. Kochak and S. Sharma, “Demand Forcasting Using Neural Network For Supply Chain Managemnt,” Int. J. Mech. Eng. Robot. Res., vol. 4, no. 1, pp. 97–104, 2015.
-
[2] R. Hidayat and Suprapto, “Meminimalisasi Nilai Error Peramalan Dengan Algoritma Extreme Learning Machine,” J. Optimasi Sist. Ind., vol. 11, no. 1, pp. 187–192, 2012.
-
[3] J. S. D. Raharjo, “Model Artificial Neural Network based on Particle Swarm Optimization Model For Inflation Rate Forecast,” J. Sist. Komput., vol. 3, no. 1, pp. 10–21, Jun. 2013.
-
[4] D. P. Fardani, E. Wuryanto, and I. Werdiningsih, “Sistem Pendukung Keputusan Peramalan Jumlah Kunjungan Pasien Menggunakan Metode Extreme Learning Machine (Studi Kasus: Poli Gigi Rsu Dr. Wahidin Sudiro Husodo Mojokerto),” J. Inf. Syst. Eng. Bus. Intell., vol. 1, no. 1, Apr. 2015.
-
[5] D. A. R. Wati and Y. A. Rochman, “Model Penjadwalan Matakuliah Secara Otomatis Berbasis Algoritma Particle Swarm Optimization (PSO),” J. Rekayasa Sist. Ind., vol. 2, no. 1, 2013.
Susila Handika: Perbandingan Metode Extrame learning …
p-ISSN:1693 – 2951; e-ISSN: 2503-2372
-
[6] B. Santosa and P. Willy, Metode Metaheuristik, Konsep dan Implementasi, 1st ed. Surabaya: Guna Widya, 2011.
-
[7] S. Makridakis, S. C. Wheelwright, and R. J. Hyndman, Forecasting Methods And Applications, 3rd Ed. Wiley India Pvt. Limited, 2008.
-
[8] K. G. Sheela, S. N. Deepa, K. G. Sheela, and S. N. Deepa, “Review on Methods to Fix Number of Hidden Neurons in Neural Networks, Review on Methods to Fix Number of Hidden Neurons in Neural Networks,” Math. Probl. Eng. Math. Probl. Eng., vol. 2013, 2013, p. e425740, Jun. 2013.
-
[9] R. J. Hyndman and G. Athanasopoulos, Forecasting: principles and practice. OTexts, 2014.
-
[10] Q. Hua Liang, “Improving the Conditioning of Extreme Learning Machine by Using Particle Swarm Optimization,” Int. J. Digit. Content Technol. Its Appl., vol. 6, no. 2, pp. 85–93, Feb. 2012.
ISSN 1693 – 2951
Susila Handika Perbandingan Methode Extrame Lear …
Discussion and feedback