SISTEM VERIFIKASI BIOMETRIKA TELAPAK TANGAN DENGAN METODE DIMENSI FRAKTAL DAN LACUNARITY
on
Sistem Verifikasi Biometrika …
Ketut Gede Darma Putra
SISTEM VERIFIKASI BIOMETRIKA TELAPAK TANGAN
DENGAN METODE DIMENSI FRAKTAL DAN LACUNARITY
Ketut Gede Darma Putra
Staff Pengajar Teknik Elektro, Fakultas Teknik, Universitas Udayana
Kampus Bukit Jimbaran, Bali, 80361
Email: darma.putra@ee.unud.ac.id
Abstrak
Sistem pengenalan diri secara otomatis dengan telapak tangan merupakan teknologi biometrika yang masih relatif baru. Permasalahan utama dalam sistem pengenalan dengan telapak tangan adalah bagaimana memperoleh ciri telapak tangan tersebut. Penelitian ini memperkenalkan pendekatan baru untuk menghasilkan ciri telapak tangan yaitu dimensi fraktal dan derajat kekosongan fraktal (lacunarity). Skor pencocokan dua telapak tangan dihitung dengan metrika korelasi.
Sistem diuji menggunakan sekitar 1250 telapak tangan milik 250 responden. Hasil percobaan menunjukkan sistem mampu menghasilkan tingkat keberhasilan sekitar 98% atau FAR = 1.9139 %, FRR = 1.9139%, T = 0.2364.
Kata kunci : biometrics, palmprint ,fractal dimension, lacunarity
1 PENDAHULUAN
Pada era informasi ini, kebutuhan terhadap sistem pengenalan diri (personal recognition) secara otomatis yang handal dan dapat dipercaya semakin meningkat terutama untuk sistem keamanan. Sistem pengenalan bertujuan memecahkan identitas seseorang. Terdapat dua tipe sistem pengenalan, yaitu sistem verifikasi dan identifikasi. Sistem verifikasi bertujuan untuk menerima atau menolak identitas yang diklaim oleh seseorang, sedangkan sistem identifikasi bertujuan untuk memecahkan identitas seseorang. Sistem verifikasi pada dasarnya menjawab pertanyaan “Apakah identitas saya sama dengan identitas yang saya sebutkan ?”, sedangkan sistem identifikasi pada dasarnya menjawab pertanyaan “identitas siapakah ini ?”. Dari sudut pandang kompleksitas, sistem verifikasi lebih sederhana karena hanya mencocokan satu masukan dengan satu data acuan (pencocokan 1 : 1), sedangkan sistem identifikasi mencocokan satu masukan dengan banyak data acuan (pencocokan 1 : M).
Berbagai pendekatan telah dikembangkan untuk melakukan pengenalan diri secara otomatis. Pendekatan-pendekatan tersebut pada dasarnya dapat dikelompokkan menjadi tiga, yaitu: pertama, berdasarkan pada sesuatu yang dimiliki (possessions-based), seperti kunci (physical key) dan kartu (card). Kedua, berdasarkan pada sesuatu yang diketahui (knowledge-based), seperti identitas pengguna (userid), PIN, dan password, dan ketiga, berdasarkan biometrika (biometrics-based), seperti sidik jari, wajah, suara, dan lain-lain.
Terdapat enam biometrika yang umum dipakai untuk sistem pengenalan diri, antara lain: sidik jari (fingerprint), selaput pelangi (iris), wajah (face), suara (voice), geometri tangan (hand geometry), dan tanda tangan (signature) (Nalini,2003).
Telapak tangan (palmprint) merupakan biometrika yang masih relatif baru diteliti dan
digunakan untuk sistem pengenalan Publikasi pertama tentang sistem pengenalan biometrika telapak tangan adalah tahun 1998 (Zhang,2004). Telapak tangan memiliki beberapa karakteristik unik yang sangat menjanjikan untuk digunakan pada sistem pengenalan diri.
Karakterisitik tersebut diantaranya: ciri geometri seperti: panjang, lebar, dan area telapak tangan, ciri garis-garis utama seperti: garis hati, garis kepala, dan garis kehidupan, ciri garis-garis kusut atau lemah, ciri titik delta, dan ciri minusi. Garis-garis utama dan kusut, yang sering disebut dengan ciri garis saja, memiliki beberapa kelebihan dibandingkan ciri yang dihasilkan biometrika lainnya, seperti: dapat diperoleh dari citra resolusi rendah, sulit dipalsu, dan bersifat stabil karena sedikit mengalami perubahan dalam kurun waktu lama. Telapak tangan menyediakan area yang lebih luas dibandingkan dengan sidik jari, sehingga lebih banyak ciri unik dapat dihasilkan untuk meningkatkan unjuk kerja sistem pengenalan terutama untuk sistem identifikasi. Saat akuisisi data, tidak seperti sidik jari, telapak tangan tidak menyentuh sensor sehingga tidak terdapat sisa tekanan telapak tangan yang melekat pada sensor. Kelebihan-kelebihan inilah yang menyebabkan telapak tangan mulai diminati dan diteliti.
Permasalahan penting yang harus dijawab dalam sistem pengenalan telapak tangan adalah bagaimana memperoleh ciri telapak tangan. Berbagai metode telah diperkenalkan oleh beberapa penelitian sebelumnya (Chih-Lung et al,2004; Connie et al,2003; Duta et al,2002; Kumar et al, 2004; Li et al; 2002, Pang et al,2003; Shu et al,1998; Wu et al,2004; Zhang et al,1999, Zhang et al,2004) untuk memperoleh ciri telapak tangan. Penelitian ini memperkenalkan suatu metode baru untuk memisahkan ciri telapak tangan, yaitu menggunakan metode dimensi dan derajat kekosongan fraktal.
Pemilihan metode fraktal didasari pada pertimbangan garis-garis tangan bersifat alami. Proses pembentukannya sangat dipengaruhi oleh kondisi bayi ketika berada dalam kandungan (Richards et al,2005). Garis-garis tangan bukan murni garis lurus, jumlah garis lemah atau kusut cendrung banyak dan tidak teratur, sementara fraktal adalah suatu metode yang sangat cocok untuk model alami dan keadaan yang tidak teratur.
-
2 DASAR TEORI
Titik (point) tidak memiliki dimensi karena tidak memiliki panjang, lebar maupun bobot. Garis (line) berdimensi 1 karena memiliki panjang. Bidang (plane) berdimensi 2 karena memiliki panjang dan lebar. Ruang (space) berdimensi 3, karena memiliki panjang, lebar, dan kedalaman. Bila diperhatikan, dimensi dari objek-objek Eucledian (garis, bidang, dan ruang) merupakan bilangan bulat, yaitu berturut-turut 1, 2, dan 3.
Objek-objek Fraktal dapat memiliki dimensi pecahan (fractional dimension). Metode yang umum digunakan untuk menghitung dimensi dari objek fraktal adalah metode penghitungan kotak (box counting) yang dapat dinyatakan sebagai berikut.
D (s ) = log( N (s)) (i) log(s)
dengan N(s) menyatakan banyaknya kotak berukuran s yang berisi informasi (pixel) objek, dan D(s) adalah dimensi fraktal objek dengan kotak berukuran s.
Langkah-langkah metode penghitungan kotak adalah sebagai berikut. Pertama, citra dibagi kedalam kotak-kotak dengan ukuran s. Kedua, hitung banyaknya kotak N(s) yang dibutuhkan melingkupi suatu objek. Nilai N(s) sangat tergantung pada s. Nilai s berubah dari 1 sampai 2k, dengan k = 0, 1, 2,…dan seterusnya, dan 2k tidak boleh lebih besar dari ukuran citra. Bila citra berukuran 2m x 2m, maka nilai k akan berhenti sampai m. Ketiga, hitung D(s) dengan persamaan (2.31). Langkah terakhir adalah membuat garis lurus (regresi linier) berdasarkan nilai-nilai log(N(s)) (sebagai sumbu y) dan nilai-nilai log(s) (sumbu x). Kemiringan (slope) dari garis lurus tersebut merupakan dimensi fraktal dari suatu objek.
Derajat kekosongan fraktal mengukur bagaimana fraktal mengisi ruang. Fraktal yang memiliki kepadatan tinggi, memiliki derajat kekosongan rendah. Derajat kekosongan meningkat bila tingkat kekasaran meningkat.
Derajat kekosongan dapat dihitung dengan cara sebagai berikut. Bila P(m,L) menyatakan probabilitas dari titik berjumlah m pada kotak yang berukuran L. Maka untuk setiap nilai L
N
∑ P(m, L) = 1
m =0
(2)
dengan N menyatakan banyaknya piksel pada kotak yang berukuran L.
N
M (L) = ∑ mP (m, L)
m=0
N
M 2 (L ) = ∑ m 2 P (m, L)
m=0
(3)
(4)
Derajat kekosongan dapat didefinisikan sebagai
M 2( L) -[M (L )]2 [M (L )]2
(5)
Karena derajat kekosongan menurun bila ukuran kotak (L) membesar, maka nilai L semakin kecil merupakan pilihan yang lebih baik karena akan lebih mencerminkan derajat kekosongan dari objek atau citra.
3 METODELOGI
3.1 Segmentasi ROI dan Normalisasi
Teknik segmentasi ROI, persiapan pengolahan dan normalisasi menggunakan metode pada [3][4].
Pemisahan ciri telapak tangan dilakukan dengan metode dimensi dan derajat kekosongan fraktal. Tahapan-tahapan pemisahan ciri dengan metode ini dapat dijelaskan sebagai berikut.
-
1. Garis-garis telapak tangan dideteksi dalam arah 0o, 45o, 90o, 135o, dengan cara berikut:
dengan * menyatakan operasi konvolusi, Ii, I2, I3 dan I4 berturut-turut menyatakan citra rajah telapak tangan dalam arah 0o, 45o, 90o, dan 135o , sedangkan h1, h2, h3, dan h4 merupakan tapis seperti ditunjukkan pada Gambar 1, akan tetapi ukurannya yang diperluas menjadi 9 x 9.
-1
-1 -1
-1 -1
222
-1 -1
-1
-1 2
2 -1
-1
-1
-1
2
2
2
-1
-1
-1
2
-1
-1
-1 -1
2 -1
-1
2
Gambar 1. Tapis pendeteksi garis dari kiri ke kanan berturut-turut untuk arah 0o, 45o, 90o, dan 135o
-
2. Citra I1, I2, I3 dan I4 kemudian
diambangkan dengan metode Otsu sehingga diperoleh 4 citra biner.
-
3. Setiap citra biner kemudian dipartisi menjadi M x M blok tanpa tumpang tindih. Dalam pengujian akan dicoba dua nilai M, yaitu 4 dan 8.
-
4. Selanjutnya nilai dimensi dan derajat kekosongan fraktal untuk setiap blok dihitung, sehingga diperoleh panjang vektor ciri M2 pada setiap citra biner, yang masing-masing ciri dapat dinyatakan sebagai:
vD = (d1, d2, d3, ..., dM2) untuk ciri dimensi fraktal
vL = (k1, k2, k3, ..., kM2) untuk ciri derajat kekosongan fraktal
Dimensi fraktal dan derajat kekosongan fraktal berturut-turut dihitung dengan persamaan (1) dan (5).
Gambar 2 menunjukkan hasil setiap tahapan pemisahan ciri dengan menggunakan metode DFL. Gambar (a) merupakan citra asli, gambar (b),(c),(d), dan (e) berturut-turut adalah rajah telapak tangan dalam arah 0o, 45 o, 90 o, dan 135 o, gambar (f),(g),(h), dan (i) berturut-turut adalah citra biner dari gambar (b),(c),(d), dan (e), gambar (j)-(m) dan (n)-(q) berturut-turut ciri dimensi dan derajat kekosongan fraktal dari gambar (f),(g),(h), dan (i) yang dibagi menjadi 4 x 4 blok. Panjang vektor ciri dimensi dan derajat kekosongan fraktal masing-masing adalah 64.
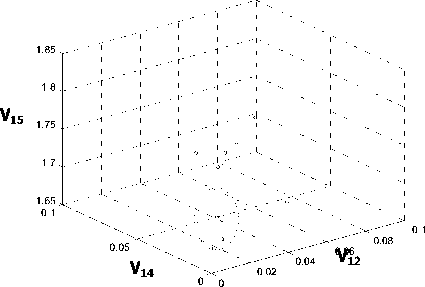
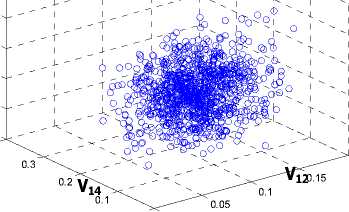
Gambar 3 (a) menyajikan korelasi tiga elemen vektor ciri dalam ruang 3D. Warna biru, hijau, dan merah berturut-turut menyatakan tiga telapak tangan pada group A, B, dan C. Gambar (b) menyajikan korelasi tiga elemen vektor ciri sekitar 1050 telapak tangan milik 210 orang.
(j) (k) (l) b≡⅜* (m) (n) (o) 1÷
(p) (q)
Gambar 2. Tahapan pemisahan ciri dengan metode dimensi dan derajat kekosongan fraktal
(a)
(a)



(d)
(b)


(g)


V15
1.85
1.8
1.75
1.7
1.65
1.6
0.4
0.05
V14
120.15
0.2
0
(b)
Gambar 3. Representasi elemen vektor ciri dalam ruang 3D. (a) tiga elemen vektor ciri group A,B,dan C, (b) tiga elemen vektor ciri untuk 1050 telapak tangan
Pencocokan antara citra uji dengan citra acuan menggunakan metrika korelasi ternormalisasi, yaitu:
8
drs =1
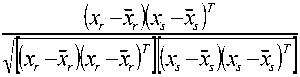
(10)
7
6
Pengguna sah
5
4
3
2
1
Pengguna tidak sah
dengan xr dan xs merupakan vektor ciri citra uji dan citra acuan. Jarak korelasi di atas memiliki jangkauan nilai antara 0 sampai dengan 1. Semakin mirip citra uji dengan citra acuan, maka nilai jarak korelasinya semakin mendekati 0, dan bila semakin tidak mirip maka nilainya mendekati 1. Untuk menentukan apakah citra uji adalah sah (genuine) atau tidak sah (impostor) digunakan suatu nilai ambang (threshold value). Bila jarak (score) lebih kecil dari nilai ambang maka pengguna dikatakan sah, bila lebih besar maka pengguna dikatakan tidak sah.
Pengujian sistem verifikasi pada penelititan ini, menggunakan sekitar 1250 citra tangan milik 250 user dengan 5 sampel untuk setiap user. Tiga citra sampel pertama digunakan sebagai citra acuan pada basisdata, sedangkan sisanya untuk pengujian.
Ada 2 jenis pengujian yang dilakukan, yaitu pertama, mencocokan ciri citra uji dengan rata-rata dari ketiga ciri citra latih, kedua, setiap citra telapak tangan yang ada pada basisdata dicocokan satu sama sehingga total pencocokan yang terjadi adalah 780625 pencocokan. Gambar 4 menunjukkan distribusi probabilitas skor pengguna sah dan tidak sah, dan Gambar 5 menunjukkan nilai FAR, FRR dan EER dengan berbagai nilai ambang, dengan hanya menggunakan ciri dimensi fraktal sehingga panjang vektor ciri adalah 64. Ciri citra acuan yang digunakan adalah ciri rata-rata dari ketiga citra acuan.
0
0
0.2 0.4 0.6 0.8
1
1.2 1.4
Skor
Gambar 4. Distribusi probabilitas skor pengguna sah dan tidak sah dengan menggunakan ciri dimensi fraktal dengan panjang vektor ciri 64
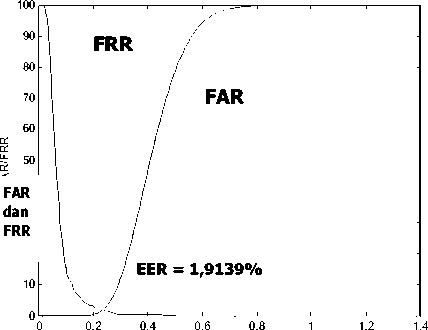
Nilai Ambang (T)
Gambar 5. Nilai FAR, FRR, dan EER dengan menggunakan ciri dimensi fraktal saja, panjang vektor ciri 64
Tabel 1 menunjukkan beberapa nilai FAR dan FRR dengan beberapa nilai ambang (T), dengan menggunakan ciri dimensi fraktal, derajat kekosongan fraktal, dan gabungan kedua ciri tersebut.
Dari Tabel 1 terlihat bahwa gabungan ciri dimensi dan derajat kekosongan fraktal tidak memberikan hasil yang lebih baik dibandingkan bila hanya menggunakan dimensi fraktal saja atau derajat kekosongan saja.
Tabel 1. Nilai FAR/FRR dengan menggunakan beberapa nilai ambang (T), dengan ciri dimensi fraktal, derajat kekosongan fraktal, dan gabungan keduanya, dengan merata-ratakan ciri citra acuan
|
T |
Dimensi Fraktal |
T |
Derajat Kekosongan |
T |
Kombinasi | |||
|
FFR(%) |
FAR(%) |
FRR(%) |
FAR(%) |
FRR(%) |
FAR(%) | |||
|
0,1714 |
2,8708 |
0,5511 |
0,1749 |
3,6683 |
0,0838 |
0,0006 |
5,7416 |
0,0619 |
|
0,1964 |
2,5518 |
0,6875 |
0,2049 |
2,5518 |
0,4366 |
0,0007 |
4,1467 |
0,2341 |
|
0,2164 |
2,3923 |
0,8670 |
0,2199 |
2,0734 |
0,8665 |
0,0008 |
3,0303 |
0,7683 |
|
0,2364 |
1,9139 |
1,9139 |
0,2399 |
1,9139 |
1,9139 |
0,0009 |
2,0734 |
2,0555 |
|
0,2564 |
1,5949 |
3,8134 |
0,2599 |
1,2759 |
3,8646 |
0,0010 |
1,7544 |
4,5594 |
|
0,2664 |
1,1164 |
5,1814 |
0,2699 |
0,9569 |
5,2294 |
0,0011 |
1,4354 |
6,2850 |
|
0,2764 |
0,7974 |
6,7732 |
0,2799 |
0,6380 |
6,8734 |
0,0012 |
1,2759 |
10,987 |
Selain membagi citra menjadi 4 x 4 blok, pengujian juga dilakukan dengan membagi citra 8 x 8 blok sehingga total panjang vektor ciri adalah 256 bila menggunakan ciri dimensi atau derajat kekosongan fraktal saja, atau 512 bila menggunakan gabungan kedua ciri tersebut. EER yang diperoleh dengan menggunakan penambahan jumlah ciri berturut-turut adalah 2,2329, 1,7544, dan 3,3493
untuk ciri dimensi fraktal, derajat kekosongan fraktal, dan gabungan dimensi dan derajat kekosongan fraktal. Hasil pengujian ini menunjukkan penambahan ciri tidak menjamin memberikan hasil yang lebih baik.
Tabel 2 menunjukkan hasil pengujian sistem verifikasi dengan tidak merata-ratakan ciri citra latih.
Tabel 2. Nilai FAR/FRR dengan menggunakan beberapa nilai ambang (T), dengan ciri dimensi fraktal, derajat kekosongan fraktal, dan gabungan keduanya, dengan tidak merata-ratakan ciri citra acuan
|
T |
Dimensi Fraktal (64 ciri) |
T |
Derajat Kekosongan (64 ciri) |
T |
Kombinasi (128 ciri) | |||
|
FRR(%) |
FAR(%) |
FRR(%) |
FAR(%) |
FRR(%) |
FAR(%) | |||
|
0,1714 |
4,7847 |
0,8679 |
0,2299 |
4,5933 |
0,7630 |
0,0008 |
7,947 |
0,1316 |
|
0,1964 |
4,3541 |
1,3338 |
0,2399 |
4,1627 |
1,1936 |
0,0009 |
5,502 |
0,4661 |
|
0,2491 |
3,8278 |
1,9538 |
0,2499 |
3,7799 |
1,7556 |
0,0010 |
4,627 |
1,3728 |
|
0,2641 |
3,1579 |
3,2466 |
0,2649 |
2,9665 |
2,9709 |
0,0011 |
3,0144 |
3,2168 |
|
0,2741 |
2,9187 |
4,3912 |
0,2749 |
2,5837 |
4,0788 |
0,0012 |
2,880 |
6,3962 |
|
0,2841 |
2,3923 |
5,8364 |
0,2849 |
2,1531 |
5,4724 |
0,0013 |
2,053 |
1,1132 |
|
0,2941 |
2,2010 |
7,5937 |
0,2949 |
1,7703 |
7,1610 |
0,0014 |
1,789 |
1,7274 |
Berdasarkan Tabel 1 dan Tabel 2 terlihat bahwa unjuk kerja sistem verifikasi dengan menggunakan rata-rata ciri citra latih lebih baik dibandingkan dengan tanpa merata-ratakan ciri citra acuan.
Berdasarkan hasil percobaan, sistem verifikasi biometrika telapak tangan ini memiliki unjuk kerja yang tinggi, terbukti dari nilai FAR, FRR, dan EER sistem ini kecil atau memiliki tingkat akurasi tinggi yaitu tingkat akurasi mencapai 98% atau FAR = 1.9139 %, FRR = 1.9139%, T = 0.2364. Unjuk kerja tingi pada sistem ini dipengaruhi juga oleh proses
segmentasi, persiapan pengolahan, dan normalisasi yang diperkenalkan oleh Darma Putra, 2006.
-
[1] . Cheng S., 2004, “Feature Extraction of Medical Images Based on the Fractal Charateristics”, http://stut.edu.tw, 20 oktober 2004.
-
[2] . Caetanno T.Jr., Agma Traina, Leejay Wu, Christos F., 2004, “Fast feature selection using fractal dimension”, http://cs.cmu.edu, 11
Nopember 2004.
-
[3] . Darma Putra, IKG. 2006. Disertasi: Metode Fraktal untuk Sistem Pengenalan Biometrika Telapak Tangan. Yogyakarta: Universitas Gadjah Mada.
-
[4] . Darma Putra, Adhi Susanto, Agus Harjoko, Thomas Sri Widodo, 2005, “Sistem Verifikasi dengan Biometrika Telapak Tangan” , Prosiding, UTY Jogjakarta.
-
[5] . Kumar A., David C.M.Wong, Helen C.Shen, Anil K.Jain, 2004, Personal Verification using Palmprint and Hand Geometry Biometric, http://www.biometrics.cse.msu.edu/Kumar_AV BPA2003.pdf, 12 Maret 2004.
-
[6] . Liu Y., Yanda Li, 1997, “Image Feature Extraction and Segmentation using Fractal Dimension”, International Conference on Information, Communication and Signal Processing.
-
[7] . Nalini K.R., Andrew Senior, Ruud M.Bolle, 2003, “Automated Biometrics”, http://us.ibm.com, 24 Mei 2003.
-
[8] . Pratt W.K., 1991, “Digital Image Processing, Second Edition”, John Wiley & Sons.
-
[9] . Zhang D., 2004, “Biometrics – An Unique Authentication Approach”,
http://www4.comp.polyu.edu.hk/~hkbas/, Juli 2005
Teknologi Elektro
6
Vol. 8 No.2 Juli - Desember 2009
Discussion and feedback