Pengaruh Kontrol Optimal Pada Model Penyebaran Penyakit Menggunakan Runge-Kutta Orde 4

Jurnal Matematika Vol. 13, No.1, Juni 2023, pp. 25-40

Article DOI: 10.24843/JMAT.2023.v13.i01.p158

ISSN: 1693-1394

Pengaruh Kontrol Optimal Pada Model Penyebaran Penyakit Menggunakan Runge-Kutta Orde 4

MNH Qomarudin

Universitas Nahdlatul Ulama Blitar e-mail: [email protected]

RR Robby

Universitas Nahdlatul Ulama Blitar e-mail: [email protected]

R Akbarita

Universitas Nahdlatul Ulama Blitar e-mail: [email protected]

Abstract: In the area of mathematics, optimal control is a method for making complex and dynamic decisions. For instance, numerous researchers employ optimum control to determine the best circumstances to control a disease and stop the spread of various diseases. As a result, observations will be made in this study about the comparison of an infectious disease spread dynamic system with and without controls. As of this study, observations are produced by providing control construction on the given model and a number of examples of dynamic system problems (with and without control). After that, both models received numerical simulations. Based on the observations, it is possible to draw the conclusion that a disease's best control, whether achieved by treatment controls or preventive controls like immunizations, depends on the disease's mode of transmission. The spread of infectious diseases can be effectively controlled utilizing treatment processes and preventative processes, such as immunizations, administered widely within the first three months. By accelerating the healing process for infected people and using immunizations in combination, this control can be accomplished.

Keywords: Optimal control, numerical simulation, Dynamical system

Abstrak: Kontrol optimal merupakan salah satu alat dalam bidang matematika dalam pembuatan keputusan yang dinamis dan kompleks. Sebagai contoh optimal kontrol ini digunakan oleh berbagai peneliti dalam upaya mencegah berbagai penyebaran penyakit hingga mencari kondisi optimal dalam mengendalikan suatu penyakit. Oleh karena itu pada penelitian ini akan dilakukan pengamatan mengenai perbandingan suatu sistem dinamik penyebaran penyakit menular dengan menggunakan kontrol dan tanpa kontrol. Pada penulisan ini pengamatan dilakukan dengan memberikan beberapa contoh permasalahan sistem dinamik (dengan dan tanpa kontrol) dan

kemudian memberikan konstruksi kontrol pada model yang telah diperoleh. Setelah melakukan konstruksi pada model yang diperoleh simulasi numerik diberikan pada kedua model tersebut. Berdasarkan pengamatan yang telah dilakukan diperoleh kesimpulan bahwa kontrol optimal pada suatu penyakit menggunakan kontrol pengobatan maupun kontrol pencegahan berupa vaksinasi memberikan efek yang berbeda-beda tergantung pada bagaimana suatu penyakit bertransmisi. Kontrol optimal dengan menggunakan proses pengobatan maupun proses pencegahan berupa vaksinasi yang dilakukan secara masif di tiga bulan pertama memberikan hasil yang baik dalam mengendalikan penyebaran penyakit menular. Pengendalian tersebut dapat dilakukan dengan memaksimalkan proses pengobatan pada korban terinfeksi beserta menggunakan vaksinasi dalam upaya mencegah seseorang terinfeksi suatu penyakit.

Kata kunci:Kontrol optimal, simulasi numerik, sistem dinamik

• 1.    PENDAHULUAN

Kontrol optimal adalah metode standar dalam menyelesaikan permasalahan dinamis yang diekspresikan dalam waktu kontinu. Kontrol tersebut merupakan salah satu alat dalam bidang matematika yang sangat ampuh dalam pembuatan suatu keputusan dimana keputusan itu melibatkan suatu sistem dinamis dan kompleks. Pada mulanya pengembangan mengenai teori kontrol optimal dikembangkan oleh L.S Pontryagin bersama teman-temanya pada tahun 1962 dan dituliskan dalam (Naidu, 2003). Teori kontrol optimal tersebut merupakan proses penentuan lintasan kontrol dan dan variabel-variabel state pada sistem dinamis selama waktu yang ditentukan dengan meminimalkan indeks performansi (Kahuru, Luboobi, & Nkansah, 2017).

Pada berbagai praktek, teori tersebut telah digunakan dalam berbagai permasalahan dinamis untuk membuat suatu strategi pengendalian pada sebuah sistem. Sebagai contoh dalam menangani suatu wabah telah digunakan teori kontrol optimal guna membuat sebuah keputusan dalam pengendalian wabah tersebut. Kontrol optimal tersebut dinyatakan sebagai u(t) yang diartikan sebagai rata-rata proses vaksinasi dan diberikan pada sistem sebagai kontrol kepada individu rentan terhadap penyakit (Jana, Haidar, & Kar, 2016). Pada penelitian yang lain, masalah kontrol optimal ini juga telah digunakan oleh Da-peng Gao dan Nan-jing Huang pada tahun 2017 dalam melakukan pengendalian terhadap penyakit Tubercolousis. Da-peng Gao dan Nan-jing Huang pada penelitian tersebut menggunakan tiga kendali utama yaitu U₁ sebagai kontrol vaksinasi, U₂ kontrol yang dinyatakan sebagai kesuksesan dalam proses penyembuhan beserta U₃ yang merupakan kontrol terhadap proses kesembuhan individu terinfeksi. Dengan menggunakan ketiga kontrol tersebut, Da-peng Gao dan Nan-jing Huang berhasil meminimalkan jumlah korban terinfeksi beserta biaya dari proses pengendalian yang diberikan (Da-peng & Nan-jing, 2017).

Pada penelitian lain yakni yang dituliskan oleh Haileyesus Tessema Alemneh dan Negesse Yizengaw Alemu pada tahun 2021 mengenai kecanduan seseorang terhadap penggunaan media sosial juga menggunakan teori kontrol optimal guna melakukan pengendalian terhadap kecanduan tersebut. Pada penelitian tersebut kasus-kasus mengenai kecanduan media sosial

digambarkan dalam bentuk model matematika deterministik SEARQ yang terdiri dari empat kelas yaitu S (susceptible), E (exposed), A (addicted), R (recovered), dan Q (quit) yang merupakan jumlah individu yang berhenti menggunakan media sosial. Pada penelitian tersebut digunakan dua bentuk kontrol optimal dalam melakukan pengendalian kasus tersebut yaitu melalui pendidikan dan iklan beserta treatment bagi orang yang telah mengalami kecanduan media sosial. Dengan menggunakan dua kontrol tersebut diperoleh kesimpulan bahwa dengan melakukan kombinasi dua kontrol tersebut, maka kasus-kasus kecanduan media sosial dapat dikurangi dengan baik (Alemneh & Alemu, 2021).

Berdasarkan pemaparan yang telah diberikan, perilaku sistem dinamis memberikan hasil yang berbeda saat ada atau tidak adanya kontrol. Oleh karena itu pada penulisan ini, akan dilakukan pengamatan mengenai perbedaan model sistem dinamis penyebaran penyakit saat diberikan kontrol baik proses pengobatan dan vaksinasi dibandingkan dengan tanpa kontrol. Pengamatan tersebut dilakukan dengan melakukan analisis pada penyelesaian numerik model dinamis Runge-Kutta Orde 4. Selanjutnya pada penulisan ini analisis akan dilakukan pada beberapa contoh kasus dimana perbandingan tersebut melibatkan satu atau lebih variabel state yang diberikan.

• 2.    METODE PENELITIAN

  2.1 Prinsip Dasar Pontryagin

  Jika diberikan persamaan pembangkit sebagai berikut x(t) = f(x, u(t),t)

  
  

  dengan fungsi objektif yaitu

  J = S(x(tf),tf) +

  
  

  ∫

  ^j t₀

  
  

  v(x(t),u(t))dt

  
  

  (1)

  (2)

  
  

Dalam hal ini kondisi batas yang diberikan adalah x(t₀) = x₀ dan x(tf) = xf sedemikian hingga untuk mencari solusi permasalahan optimal kontrol tersebut adalah dengan melakukan langkah-langkah sebagai berikut:

• 1)    Pembentukan fungsi pontryagin berdasarkan permasalahan optimal kontrol yang diberikan dengan

H(x(t),u(t),λ(t),t) = V(x(t),u(t),t) + λ'(t) f(x(t),u(t),t)

Dimana u merupakan parameter kontrol, λ(t) merupakan variabel costate, x(t) yang merupakan variabel state, dan t merupakan variabel waktu.

^dengan O = ⁰

2)

3)

Penentuan nilai minimal ^ berdasakan u(t). Dalam hal ini

sedemikian hingga diperoleh u*(t) = h(x*(t), λ*(t),t)

Selanjutnya dengan menggunakan langkah pada poin 1 maka dapat diperoleh bentuk

fungsi hamiltonian atas permasalahan optimal kontrol dan dengan poin 2 maka dapat

diperoleh nilai optimal pada W* berdasarkan nilai u*(t) yang optimal.

4)

Setelah melakukan langkah ketiga, maka akan diperoleh sistem persamaan differensial beserta kondisi awal dan kondisi akhir yang diinginkan dimana sistem persamaan differensial tersebut terdiri atas persamaan state dan costate, sedemikian hingga pada tahap ini langkah yang dilakukan adalah menyelesaikan persamaan yang diperoleh yakni

z . ∂H X*(t) =

∂λ

λ*(t} = -^d∂i ∂x

dengan kondisi awal X₀

dan kondisi akhir [^^, + ^^]  δt f

^+[O* -«< -

• 5)    Pada tahap yang terakhir subsitusikan hasil yang diperoleh yaitu x* (t) dan λ* (t) pada tahap-4 kedalam ekspresi u* (t) di tahap ke dua untuk memperoleh nilai dari optimal kontrol.

• 2.2    Tipe-Tipe Sistem

Berdasarkan kondisi batas yang diperoleh, maka terdapat beberapa tipe sistem pada prinsip dasar pontryagin yaitu:

• 1)    Waktu akhir yang tetap dan kondisi state system akhir yang tetap dimana δtf = 0 dan δXf = 0 dengan kondisi yang diberikan pada tipe ini adalah x(t₀) = X₀, x(tf) = Xf

• 2)    Waktu akhir tak tetap dan kondisi state system akhir yang tetap. Subsitusi pada tipe ini adalah δtf ≠ 0 dan δXf = 0 dimana kondisi yang diberikan pada tipe ini adalah x(t₀) =

X0, xM = Xf,∖tH*+%]  =0

L         ^^t ^tf

• 3)    Waktu akhir yang tetap dan state system akhir tak tetap dengan subsitusi δtf = 0 dan

  ^λ*⅛M≡K

  
  

δxf ≠ 0 dengan kondisi batas yang diberikan x(t₀) = x₀

• 4)    Waktu akhir dan kondisi state system akhir yang terikat. Dalam hal ini subsitusi yang diberikan yaitu δXf = θ(tf) δtf dengan kondisi batas yang diberikan x(t₀) = X₀, x⅛) = e(t_f), [%* + f⁺ {Q ^{- λ}* ω}⅝)] t,

• 5)    Waktu akhir dan kondisi state system akhir yang bebas. Subsitusi yang diberikan pada tipe ini adalah δtf ≠ 0 dan δXf ≠ 0 dengan kondisi batas sebagai berikut δx(t₀) = X₀, [π*+y]  = 0, [(∂S) -λ*(t)]   = 0(Naidu, D.S., 2003).

V^^t_f      LK_θX∕*        tf

• 2.3    Metode Runge Kutta Orde-4

Metode runge-kutta merupakan metode yang menghilangkan keperluan dalam melakukan perhitungan pada turunan f(t,y).

Teorema 2.1 Diberikan f(t,y} dan semua turunan parsialnya untuk order kurang atau sama dengan n + 1 yang kontinu pada D = {(t,y)∣a ≤ t ≤ b, c ≤ y ≤ d], dan diberikan (t₀,y₀) ∈ D. Dalam hal ini, untuk setiap (t,y) ∈ D terdapat f diatnara t dan t₀ beserta μ diantara y dan y₀ dengan

f(t,y) = P_n(t,y) + R_n⁽t,y)

dimana

⅞(t,y) = ∕¼,yo) + [(t

—

∂f                ∂f      1

to) ^gi(^to^,yo') ^{+ (}y ^— yo)g^(^to^,yo)]

Γ           ∂²f                             ∂²f

⁺ l^(t—to)² nκ (^t°^,yo^)+(t—to)y^—yo)∂^(^to^,yo) ∂²f

+ ⁽y — yo⁾² ^₂(Wo)! + ...

I n

∂ⁿf

∂ t^n-j∂y^j

(toJo)j

⅛ ∑(D (^t—t«^)n-,(y^—y«⁾'

■ =0

Dengan

1   ⁿ+¹ n ₊ ι∖                         ∂ⁿ⁺¹ f

^Rn(t’^y) = (n+ 1)! Σ ⁽ j ) ^{(t — t}0^ ^{7+ (y — yo)}+}  ∂tⁿ-i+^∂yi^'^

j=o

(Burden & Faires , 2011)

Dalam hal ini algoritma standar dalam melakukan langkah numerik pada metode runge-kutte dimana elemen ke i menyatakan vektor elemen ke i^th beserta elemen vektor ke j = N + 2 — i dapat dinyatakan sebagai berikut

Forward RK4	Backward RK4
K1 =KtilXilUi) κ2=f(t +∖'xi +1K1’1^U) κ3=f(t + ^i +^K2’1AUi) K4 = f(ti + h,xi + ħK3,ui+1) ħ. Xi+1 = Xi +  (K1 + 2K2 + 2K3 + K4)	K1 = f(tj,λj,xj,uj) K2= f(tj^h,λj^hK1)-ΔxJ-Δu∖ ∖        Ad            Ad       Ad         Ad        Z K3=f(tj^,λj^hK2,hxb1Δui} ∖         Ad            Ad       Ad         Ad        Z K4 = f(tj — ħ,λj — ħK3,xj-1,Uj-1) ħ λj_1 = λj — -(K1+2K2 + 2K3 + K4)

• 3.    HASIL DAN PEMBAHASAN

Pada bagian ini akan diberikan beberapa contoh untuk membandingkan antara suatu model dinamik penyebaran penyakit dengan dan tanpa kontrol optimal dimana kontrol tersebut menggunakan kendali berupa proses pengobatan maupun proses vaksinasi.

• 3.1    Kasus 1 : Model penyebaran virus flu burung

Pada kasus yang pertama akan diberikan konstruksi model berdasarkan penelitian yang dilakukan oleh Herrera dan Gilberto pada (Herrera, J.L., & Gonzalez-Parra, G., 2011) dimana populasi pada model ini dibagi menjadi subpopulasi rentan (subsceptible) S dan susbpopulasi terinfeksi (infected) ∕. Pada kasus tersebut β merupakan rata-rata transmisi virus antara individu rentan dan terinfeksi. Dalam hal ini berdasarkan pada (Regbetade, S.A, et al, 2018) model

tersebut dikonstruksikan kembali dengan menambahkan tingkat kelahiran individu yang dinyatakan dengan Λ dan memasuki kelas susceptible. Laju kematian alami dinyatakan dengan μ, dimana r adalah tingkat kematian akibat penyakit. Sehingga konstruksi model ini dapat dituliskan pada persamaan (3)

dS

— —Λ — μS—βSI dt

dI

— — βSI—(μ + r)I

(3)

Sejumlah individu rentan yang mengalami infeksi akan memasuki populasi terinfeksi dan menambah jumlah populasi pada kelas tersebut. Oleh karena itu pada contoh ini kontrol yang diberikan berguna untuk mengurangi jumlah individu terinfeksi I dan dinyatakan sebagai u dimana kontrol tersebut merupakan proses pengobatan khusus yang diberikan pada individu terinfeksi. Sehigga diperoleh konstruksi model pada persamaan (3) yaitu

dS

— Λ — μ S — βSI + uI dt

dI

~ = βSI — (μ + r')I — uI dt

(4)

Pada konstruksi (4), uI menyatakan jumlah keberhasilan individu terinfeksi yang menjadi sehat dikarenakan proses pengobatan pada setiap waktu t. Sehingga permasalahan optimal kontrol pada contoh ini adalah dengan meminimalisasi fungsional objektif sebagai berikut

J(u) = ∫ A₀ I(t) + - u²(t) dt 02

(5)

dimana subjek 0 ≤ u(t) ≤ u_max dengan t ∈ [θ, t^]. Dalam hal ini A, A₀ merupakan bobot harga dari proses pengobatan dan t^ adalah waktu dalam menjalani pengobatan tersebut. Sehingga berdasarkan (Naidu, 2003) maka bentuk Lagrangian pada contoh ini yaitu

£(I, u) = A₀ I(t) +^u² (t) dt

Dimana bentuk hamiltonian berdasarkan bentuk Lagrange (6) dan sistem (4) adalah

H = £(I,u) +λ₁S +λ₂I

(6)

(7)

Dengan kondisi batas λ_i(t^) = 0 untuk i = 1,2. Selanjutnya nilai optimal u* pada contoh ini ∂H

dapat diperoleh dengan melakukan perhitungan pada — = 0 sedemikian hingga diperoleh

Au + λι I — λ2 I — 0 maka

(8)

* _^(λ2 ^{— λ}1^{)I u} = A

(9)

Menurut pengamatan yang dituliskan pada (Da-peng Gao, Nan-jing Huang , 2017), maka nilai optimal u dapat diperoleh berdasarkan persamaan (9) sebagai berikut

* f         (^λ2

u* = mιnγmaxl 0,—

—

A

λι)n      i

(, ^umax (

(10)

Tahap berikutnya berdasarkan bentuk Hamiltonian (7) maka dicari persamaan state dengan S = ^H- dan I = ^H∙, beserta persamaan costate yaitu λ₁ = ^H dan λ₂ = ^^. Dalam hal ini dapat diperoleh persamaan state seperti pada (3) dan persamaan costate pada persamaan (11) dengan kondisi batas λ_i(tf) = 0.

λι = ^1 M + (^ι — λ2)βI

(11)

^λ2 — ^-^o ⁺ Gk ^- λ^}^βS + (λ2 ^{- λ}ι)^u + (μ + r)λ2

Gambar 1. Jumlah populasi S pada kasus pertama dengan dan tanpa optimal kontrol

Gambar 2. Jumlah populasi I pada kasus pertama dengan dan tanpa optimal kontrol

Gambar 3. Kontrol optimal u(t) pada kasus pertama

Simulasi numerik yang diberikan pada kasus pertama dengan mengambil asumsi dari nilai-nilai parameter yaitu A — 0.0982, β — 0.2, μ — 0.032, r — 0.4, u_max — 1, A — 500, dan A₀ — 250. Seperti yang diberikan pada Gambar 1 dalam waktu 100 hari jumlah individu susceptible mengalami kenaikan sedemikian hingga jumlah individu S'usce'ptible dengan kontrol pengobatan memiliki jumlah lebih banyak jika dibandingkan dengan tanpa kontrol. Adanya kontrol terhadap proses pengobatan tersebut juga menyebabkan jumlah individu terinfeksi flu burung (dengan kontrol) lebih sedikit jika dibandingkan dengan jumlah individu terinfeksi (tanpa kontrol) seperti pada Gambar 2. Berdasarkan Gambar 3 terlihat bahwa proses pengobatan untuk mengurangi jumlah individu terinfeksi penyakit flu burung harus dilakukan secara masif dalam 15 hari pertama dan sedikit mengalami kenaikan (dalam melakukan proses pengobatan) setelah 70-100 hari. Hal tersebut harus dilakukan guna menyembuhkan individu terinfeksi agar menjadi sehat sedemikian hingga dapat mengurangi dampak buruk akan adanya infeksi penyakit tersebut.

• 3.2    Kasus 2: Model SIR Penyebaran Virus Ebola

Pada kasus yang kedua dilakukan pembahasan mengenai model SIR penyebaran virus ebola yang diberikan oleh Amira Rachah dan Defin F.M Tores tahun 2015 sebagai berikut

dS dt

-βSI

dR

dt   ^μj

d!

= βSI~μI

(12)

N(t) = S (t) + Kt) + R(t)

Dengan N konstan dalam hal ini S,! dan R merupakan subpopulasi rentan (subsceptible), terinfeksi virus ebola (infected), dan R subpopulasi yang mengalami penyembuhan akibat penyakit. Dalam hal ini β merupakan rata-rata infeksi akibat adanya kontak individu rentan dan individu terinfeksi, sedangkan μ merupakan rata-rata recovery pada individu terinfeksi (Rachah, Amira, & Torres, D.F.M. , 2015). Selanjutnya sejumlah individu rentan yang mengalami infeksi penyakit akan memasuki kelas ! sehingga kontrol yang diberikan pada model (12) berguna untuk mengurangi jumlah individu terinfeksi yang memasuki kelas !. Berdasarkan (Da-peng Gao, Nan-jing Huang, 2017) untuk mengurangi jumlah infeksi pada penyebaran virus ebola, maka dapat digunakan suatu proses vaksinasi pada sejumlah individu rentan sebelum mereka terinfeksi. Oleh karena itu konstruksi model (12) dituliskan seperti pada persamaan (13)

dS

— =-βS!-uS dt

d!

=βS!-μ!

dR

— = μ! + uS dt

(13)

Pada konstruksi (13) tersebut u(t) merupakan rata-rata vaksinasi virus ebola pada individu

rentan pada setiap waktu t. Setelah mendapatkan vaksin individu rentan akan memasuki kelas recovery dimana individu tersebut menjadi kebal terhadap virus. Namun harga vaksin pada

setiap proses pengobatan tidaklah murah. Oleh karena itu berdasarkan (Kumar, Anuj, &

Srivastava, P.K., 2017) konstruksi ini bertujuan untuk mengurangi jumlah terinfeksi dengan

meminimalisasi harga (cost) dari proses vaksinasi. Sehingga permasalahan optimal kontrol pada

contoh ini adalah meminimalisasi fungsional objektif sebagai berikut

'^,'             A

J(u)= I !(t) + — u² (t) dt

J o          ²

(14)

Dengan kontrol 0≤ u(t)≤u_max dimana t∈ [θ>tf∖- A merupakan bobot harga vaksinasi dan tf adalah lama periode dari vaksinasi. Sehingga dengan menggunakan cara yang sama seperti

pada kasus 1 dapat diperoleh nilai optimal u* sebagai berikut

u* = min

(    ( (A₁-A₃)S]     ]

{^max{^0,----—----}^,u_ma_x }

(15)

Selanjutnya persamaan state yang diperoleh seperti untuk kasus ini seperti pada (13) dan persamaan costate dapat dinyatakan sebagai berikut

λι = (λι — λ^)β! + (Ai — λ3)u                   ^A3 = 0

^λ2 = ^{— 1 + (λ}1^—λ2^{)βS +} (^λ2^{- λ}3)μ                                     ⁽¹⁶⁾

Dimana berlaku kondisi batas kondisi batas λ_i (tf} = 0 untuk i = 1,2,3.

Hasil simulasi numerik telah diperoleh pada kasus kedua dengan β = 0.437, μ = 0.032, dan A = 200 dengan u_max = 1 sebagai asumsi. Terlihat seperti pada Gambar 4 setelah 22 hari proses vaksinasi dilakukan, maka jumlah individu susceptible (rentan) dengan kontrol vaksinasi

memiliki jumlah lebih banyak jika dibandingkan dengan jumlah individu rentan tanpa kontrol. Pada Gambar 5 terlihat jelas bahwa setelah adanya kontrol vaksinasi yang diberikan, individu terinfeksi dengan kontrol vaksinasi memiliki jumlah yang lebih sedikit jika dibandingkan tanpa adanya proses vaksinasi. Kedua hal tersebut juga menyebabkan individu yang mengalami recovery (penyembuhan) dengan kontrol juga memiliki jumlah yang lebih banyak daripada tanpa kontrol di 50 hari pertama, meskipun setelah itu jumlah individu recovery tanpa kontrol sedikit lebih banyak jika dibandingkan dengan adanya kontrol vaksinasi seperti pada Gambar 6. Ketiga hal tersebut dapat terjadi dengan baik jika kontrol vaksinasi dilakukan dengan efektif pada 50 hari pertama seperti terlihat pada Gambar 7. Oleh karena itu jika proses vaksinasi dilakukan dengan baik setidaknya 50 hari pertama agar jumlah individu terinfeksi dapat dikurangi dengan optimal.

Gambar 4. Jumlah populasi S pada kasus kedua dengan dan tanpa optimal kontrol

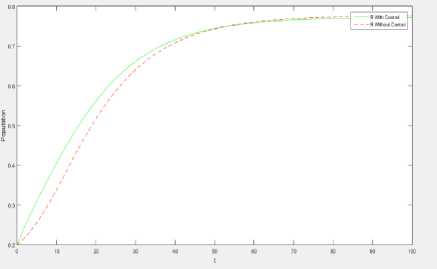
Gambar 5. Jumlah populasi I pada kasus kedua dengan dan tanpa optimal kontrol

Gambar 6. Jumlah populasi R pada kasus kedua dengan dan tanpa optimal kontrol

Gambar 7. Kontrol optimal u pada kasus kedua

• 3.3    Kasus 3: Model Matematika SIR Pada Penyakit Tuberkolosis

Pada contoh yang ketiga model SIR akan sedikit dikembangkan dengan adanya rata-rata kelahiran yang diasumsikan memasuki individu rentan seperti pada jurnal yang dituliskan oleh Yasin Ucakan dkk pada tahun 2021. Model tersebut diberikan dalam bentuk sebagai berikut

dS

~r = bN dt

βSI ~N

— μS

d!

— = βS1—μ1 — γ1 dt

dR

— = γ^μR dt

N=S+1+R

(17)

Sama seperti contoh sebelumnya, S merupakan jumlah populasi susceptible (rentan), 1 adalah jumlah individu infected, dan R merupakan individu recovery. β > 0 merupakan parameter transmisi virus akibat adanya kontak antara indvidu rentan dan individu terinfeksi.

Selanjutnya γ < 1 merupakan rata-rata proses penyembuhan pada individu terinfeksi hingga memasuki kelas recovery. Dalam hal ini, μ merupakan rata-rata kematian alami dan b adalah rata-rata kelahiran alami yang memasuki kelas susceptible (Yasin U., et al., 2021).

Untuk mengendalikan virus pada model (17) maka kontrol yang dapat dilakukan yaitu dengan mengadakan suatu proses vaksinasi untuk mengurangi jumlah individu yang terinfeksi. Dalam hal ini, konstruksi model yang dapat diberikan pada contoh ketiga dapat diberikan seperti

pada persamaan (18). Dimana u merupakan parameter kontrol yang merupakan proses vaksinasi. Selanjutnya individu susceptible akan memasuki kelas recovery setelah diberikan vaksin pada individu rentan.

— = bN —  — μS — us            — - —Ir μR+us

dt         N^                         dt                                 (18)

dl

— =βS1—μ1 — γ1

dt

Berdasarkan (Okosun, K.O.,  & Makinde, O.D., 2014) fungsional objektif dapat diberikan

dalam bentuk sebagai berikut

Ku) = ∫ j 0

^tf

A1(t) + — u²(t) dt

(19)

dengan 0 < u(t) ≤ u_max dimana t ∈ [0, t^ ] dan A,B merupakan bobot dari harga vaksinasi yang dapat diartikan sebagai harga total dari semua proses kegiatan vaksinasi. Oleh karena itu,

tujuan utama pada contoh ini adalah meminimalkan biaya dan mengurangi jumlah korban terinfeksi. Langkah yang sama juga dilakukan seperti pada kasus 1 dan kasus 2 sedemikian

diperoleh nilai optimum u* yaitu

u* = min

i I_n ⁽¹‘—¹≈>^sl      1

{maxt0,---------i,u_maχi

(20)

Dengan persamaan state seperti pada (18) dan persamaan costate yaitu

K

(λ₁—λ2)β1 N

+ (λι — λ₃)u + λ^μ

λ₃ = λ₃μ

(λ₁ — λ2)βS

^λ2= ^—A+--N--⁺ (^λ2 ^{— λ}3K ^{+ λ}2 μ

(21)

Pada kasus ketiga asumsi yang diambil untuk nilai-nilai parameter yang digunakan yaitu b = 0.182, β = 0.64, μ = 0.032, N = 1, γ = 0.28, dan A = 200,B = 150 dimana u_max = 1.5 guna menemukan solusi numerik pada permasalahan kontrol optimal (21). Solusi dari permasalahan kontrol optimal dapat dimati berdasarkan Gambar 8-11. Terlihat bahwa individu rentan (susceptible) dengan kontrol memiliki jumlah yang lebih banyak setelah 15 hari masa

vaksinasi. Berdasarkan Gambar 9 jumlah individu terinfeksi tuberkolosis dengan adanya kontrol jauh lebih sedikit jika dibandingkan tanpa adanya kontrol vaksinasi. Adanya kontrol vaksinasi ini menyebabkan banyaknya individu rentan yang memasuki kelas recovery dan tidak mengalami infeksi kembali. Pada pengamatan ini juga diamati bahwa populasi pada kelas recovery memiliki jumlah yang lebih banyak setelah dimulainya proses vaksinasi. Dalam hal ini keberhasilan dari kontrol dapat diperoleh jika proses vaksinasi dilakukan secara cepat dan tepat setidaknya dalam 90 hari pertama setelah adanya penyebaran penyakit tuberkolosis seperti pada Gambar 11. Oleh karena itu dengan suksesnya proses vaksinasi ini maka jumlah korban dikarenakan penyakit tuberkolosis dapat dikurangi dengan optimal.

Gambar 8. Jumlah populasi S pada kasus ketiga dengan dan tanpa optimal kontrol

Gambar 10. Jumlah populasi R pada kasus ketiga dengan dan tanpa optimal kontrol

Gambar 9. Jumlah populasi I pada kasus ketiga dengan dan tanpa optimal kontrol

Gambar 11. Kontrol optimal u(t) pada kasus ketiga

• 3.4    Kasus 4: Model SEIR Pada Pandemi Covid-19

Pada kasus terakhir model yang diberikan yaitu model SEIR untuk mengamati perkembangan virus Covid-19. Model tersebut diberikan oleh Zulfan Adi pada tahun 2020 (Putra, Z.A., & Abidin, S.A.Z, 2020) yang diberikan pada persamaan (22) dengan S merupakan jumlah individu susceptible (rentan), I adalah kelas terinfeksi, E menyatakan jumlah individu exposed, dan R merupakan jumlah individu pada kelas recovery. Kelas exposed berisikan individu yang secara tak sadar telah terinfeksi dan disebut sebagai carrier.

dS

— — -βSl - d_sS + i_sS

dE

— = βSl-aE + i_eE - d_εE

dl

dl ^{— aE}~^ ^{+ i}

I^l

_-

d₁l

(22)

dR

— = γl + i_κR-d_κR

Selanjutnya β merupakan parameter transmisi virus diakibatkan adanya kontak individu rentan dengan individu terinfeksi. Parameter d merupakan rasio kematian dimana i menyatakan rasio imigrasi yang terjadi pada masing-masing kelas. a dan γ merupakan periode inkubasi virus menuju kelas terinfeksi dan periode recovery yang terjadi saat individu terinfeksi mengalami kesembuhan (Putra, Z.A., & Abidin, S.A.Z, 2020).

Untuk melakukan pengendalian pada penyebaran virus korona, salah satu cara yang dilakukan oleh pemerintah yaitu menggunakan proses karantina (membatasi mobilitas) kepada masyarakat maupun dengan melakukan vaksinasi (nasional.kontan.co.id). Oleh karena itu untuk melakukan pengendalian pada virus korona, maka pada penelitian ini akan menggunakan kontrol berupa proses vaksinasi yang diberikan pada individu rentan. Sehingga pada model (22) akan diberikan penambahan variabel berupa rata-rata vaksinasi pada model tersebut yaitu u(t) untuk setiap t. Sedemikian hingga model (22) dapat direkonstruksi sebagai berikut

dS

— —βSl — d_sS + i_sS— uS

dE

— — βSl — aE + i_EE — d_EE

dl

dl ^{— aE}~^ ^{+ i}

I^l

_—

d₁l

dR

-^ — γl + i∏R — d_ER + uS

(23)

Dimana 0 ≤ u(t) ≤ U_max merupakan variabel kontrol yang dilakukan pada S dan kemudian memasuki kelas recovery. Pada kasus ini fungsional objektif yang diminimumkan

diberikan sebagai berikut

(24)

J(U) — ∫ Al(t) +— u²(t) dt

J o           ²

Dengan t ∈ [θ,t^] dan A, B merupakan bobot harga dari proses vaksinasi. Sehingga dapat

diperoleh nilai optimum u(t) yang dapat dituliskan sebagai berikut

u* — min

(*i max-i 0,—

_—

λ₄)S'

B

^}, ^umax^}

(25)

Pada kasus ini dapat diperoleh persamaan state seperti pada (22) dan persamaan costate yaitu

λι — (λι — λ^)βl + λ₄ ds — λι is + (λι — λ4)u

^λ2 ^— (^λ2 ^{— λ}3)^{a — λ}2ⁱE ^{+ λ}2 ^dE

(26)

λ3 — —A + (λ₄ — λ2) βS + (λ₃ — λ4) γ — λ3 ii + λ₃ di

λ4 — (d_R — i_κ)λ4

Pada kasus keempat parameter-parameter yang digunakan sebagai asumsi pengamatan yaitu β — 0.735, d_s — 0.132, i_s — 0.401, a — 0.51, i_E — 0.1, d_E — 0.433, γ — 0.48, i_i — 0.476, d_i — 0.08, i_R — 0.454, u_max — 1.67, dan d_R — 0.3 dengan bobot A — 200, serta B — 150. Proses kendali pada virus korona menggunakan program vaksinasi yang diberikan pada individu rentan (susceptible) yang kemudian individu tersebut akan memasuki kelas recovery. Sehingga terlihat berdasarkan Gambar 12 setelah hari pertama proses vaksinasi dilakukan, maka jumlah

individu rentan dengan kontrol vaksinasi jauh lebih sedikit jika dibandingkan dengan jumlah individu rentan (susceptible) tanpa kontrol.

Setelah adanya vaksinasi pada individu rentan maka individu tersebut memasuki kelas recovery dan menyebabkan jumlah individu exposed dengan kontrol lebih sedikit dibandingkan dengan jumlah individu exposed tanpa kontrol di hari-hari pertama proses vaksinasi seperti pada Gambar 13. Oleh karena itu, jumlah individu terinfeksi dengan kontrol akan jauh lebih sedikit (seperti pada Gambar 14) jika dibandingkan dengan tanpa kontrol setelah 3 hari program vaksinasi. Akibat dari proses vaksinasi ini juga dapat dilihat berdasarkan Gambar 15 dimana jumlah individu recovery jauh meningkat dengan signifikan dengan adanya kontrol vaksinasi jika dibandingkan jumlah individu recovery tanpa kontrol. Dengan adanya peningkatan jumlah individu recovery tersebut maka jumlah individu terinfeksi berkurang cukup banyak. Keberhasilan proses vaksinasi ini dapat dicapai jika dalam 5 hari pertama program ini dapat dilakukan dengan masif pada populasi rentan. Oleh karena itu dengan program vaksinasi ini diharapkan jumlah korban akibat adanya penyakit covid-19 dapat diminimalisasi dengan baik.

Gambar 12. Jumlah populasi S pada kasus keempat dengan dan tanpa optimal kontrol

Gambar 13. Jumlah populasi E pada kasus keempat dengan dan tanpa optimal kontrol

Berdasarkan contoh kasus yang telah diberikan, dapat disimpulkan bahwa pengendalian atas penyebaran penyakit perlu dilakukan agar dampak dari penyakit dapat diminimalkan. Seperti pada kasus pertama proses pengobatan terhadap penyakit flu burung harus dimaksimalkan dalam 15 hari pertama dalam melakukan penyembuhan pada individu terinfeksi. Hal tersebut perlu dilakukan secara maksimal agar korban terinfeksi virus flu burung dapat dikurangi dengan baik. Selanjutnya berdasarkan kasus kedua, kasus ketiga, dan kasus keempat kontrol yang digunakan dalam menanggulangi penyebaran virus tersebut yakni rata-rata vaksinasi diberikan pada individu susceptible guna mencegah seseorang terinfeksi. Dalam hal ini pada kasus kedua proses vaksinasi harus dimaksimalkan dalam 50 hari pertama guna meminimalkan jumlah individu yang terinfeksi virus ebola sedangkan pada kasus ketiga dibutuhkan setidaknya 90 hari pertama dalam melakukan vaksinasi secara masif guna mencegah penyebaran bakteri tuberkolosis. Pada kasus yang terakhir dalam upaya mencegah penyebaran Covid-19 proses vaksinasi harus dilakukan secara masif setidaknya dalam 5 hari pertama kepada setiap individu rentan agar kasus Covid-19 dapat ditanggulangi dengan baik.

Oleh karena itu dengan pengamatan yang telah dilakukan dapat disimpulkan bahwa dengan adanya kontrol optimal pada masing-masing kasus penyebaran penyakit baik dalam proses pengobatan maupun dalam proses pencegahan berupa vaksinasi, jika proses-proses tersebut dapat dilakukan secara maksimal setidaknya dalam tiga bulan pertama, maka jumlah individu terinfeksi dapat dikendalikan dengan baik. Hal tersebut dapat menjadi suatu gambaran kepada para petugas terkait dalam melaksanakan pengendalian pada penyebaran penyakit. Dalam hal ini, petugas kesehatan dapat membuat suatu strategi agar penyebaran penyakit dapat diminimalisasi. Dimana proses pengendalian dalam suatu penyebaran penyakit dapat dikendalikan dengan cara melakukan pencegahan (vaksinasi), pengobatan, ataupun keduanya yang dilakukan secara masif setidaknya dalam 3 bulan pertama agar jumlah korban dari suatu penyakit dapat dikendalikan dan dapat diminimalkan dengan baik.

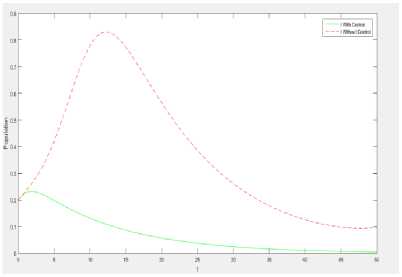
Gambar 14. Jumlah populasi I pada kasus keempat dengan dan tanpa optimal kontrol

Gambar 15. Jumlah populasi R pada kasus keempat dengan dan tanpa optimal kontrol

Gambar 16. Kontrol optimal u(t) pada kasus keempat

• 4.    KESIMPULAN DAN SARAN

Kontrol optimal pada suatu penyakit menggunakan kendali pengobatan maupun kontrol pencegahan berupa vaksinasi memberikan efek yang berbeda-beda tergantung pada bagaimana suatu penyakit bertransmisi. Dalam hal ini kontrol penyakit berupa pengobatan maupun vaksinasi secara maksimal harus dilakukan. Kontrol tersebut dapat dilakukan secara masif di tiga bulan pertama agar memberikan hasil yang sangat baik dalam mengendalikan penyebaran penyakit menular. Oleh karena itu diperlukan suatu kebijakan dan strategi dari petugas terkait

guna memaksimalkan berbagai kegiatan dalam menanggulangi penyebaran penyakit menular. Hal tersebut harus dilakukan secara maksimal sedemikian hingga dampak dari infeksi dan peyebaran penyakit tersebut dapat dikendalikan dengan baik.

Dalam hal ini selain berdasarkan pada proses pengobatan ataupun vaksinasi, langkah dalam mengendalikan penyakit menular juga bisa dilakukan dengan cara membatasi pergerakan dari setiap orang. Pergerakan tersebut didasarkan pada kontak secara langsung antara individu rentan dan individu yang telah mendapatkan infeksi. Oleh karena itu kendali pada pergerakan tiap-tiap individu tersebut juga harus diberikan agar proses pengendalian penyakit menular dapat dilakukan dengan baik. Jelas hal ini juga membutuhkan biaya program yang tidak sedikit dimana hal tersebut juga akan membatasi banyak kegiatan ekonomi suatu masyarakat. Sehingga proses pengendalian ini juga penting dilakukan secara optimal agar dampak penyebaran bisa diminimalkan dimana kendalanya adalah besarnya biaya program yang dibutuhkan dengan kegiatan ekonomi yang sangat sedikit.

DAFTAR PUSTAKA

Alemneh, H.T. & Alemu, N.Y. (2021). Mathematical Modeling With Optimal Control

Analysis of Social Media Addiction, Infectious Disease Modelling, 6 : 405 -- 419

Burden, R.L., & Faires, J.D. (2011). Numerical Analysis Ninth Edition, Brooks/Cole Cengage Learning, Boston

Da-peng Gao., Nan-jing Huang. (2017). Optimal control analysis of a tuberculosis model, Applied Mathematical Modelling (2017), doi: 10.1016/j.apm.2017.12.027

Herrera, J.L. & Gonzalez-Parra, G. (2011). Dynamical graphs for the SI epidemiological model, arXiv, https://arxiv.org/abs/1110.4070

Jana, Soovoojet., Haldar, Palash, & Kar, T.K. (2016). Optimal control and stability analysis of an epidemic model with population dispersal, Chaos, Solitons and Fractals, 83 : 6781

Kahuru, J., Luboobi, L.S., & Nkansah-Gyekye, Y. (2017). Optimal Control Techniques on a Mathematical Model for the Dynamics of Tungiasis in a Community, International Journal of Mathematics and Mathematical Sciences, 2017 : 1 -- 19

Kumar, Anuj, & Srivastava, P.K. (2017). Mathematical Vaccination and treatment as control interventions in an infectious disease model with their cost optimization , Commun Nonlinear Sci Numer Simulat, 44: 334-343

Naidu, D.S. (2003). Optimal Control System, CRC Press LLC, Boca Raton

Nasional.kontan.co.id. (2021, 02 Januari). Ini tiga langkah pemerintah cegah penularan

Covid-19 di tahun ini. Diakses pada 23 Maret 2022, dari https: //nasional. kontan.

co.id/news/ini-tiga-langkah-pemerintah-cegah-penularan-covid-19-di-tahun-ini

Okosun, K.O., & Makinde, O.D. (2014). A co-infection model of malaria and cholera diseases with optimal control , Mathematical Biosciences, 258 : 19-32

Rachah, Amira, & Torres, D.F.M. (2015). Mathematical Modelling, Simulation, and Optimal Control of the 2014 Ebola Outbreak in West Africa, Hindawi Publishing Corporation, 2015 : 1-9

Regbetade, S.A, Salawu , I.A. , & Fasanmade, P.A. (2018). Local Stability of Equilibrium Points of a SIR Mathematical Model of Infectious Diseases, World Journal of Research and Review,6 (3): 79-81

Rose, Garrett Robert. (2015). "Numerical Methods for Solving Optimal Control Problems.

Master's Thesis, University of Tennessee. http://trace.tennessee.edu/utk_{}gradthes/3401

Yasin Ucakan, Seda Gulen, & Kevser Koklu. (2021). Analysing of Tuberculosis in Turkey through SIR, SEIR and BSEIR Mathematical Models, Mathematical and Computer Modelling of Dynamical Systems, 27:1, 179-202, DOI: 10.1080/13873954.2021.1881560

40