Perbandingan Extreme Learning Machine dan Double Exponential Smoothing Untuk Meramalkan PDRB di Provinsi NTT

Jurnal Matematika Vol. 12, No.1, Juni2022, pp. 34-48

Article DOI: 10.24843/JMAT.2022.v12.i01.p147

ISSN: 1693-1394

Perbandingan Extreme Learning Machine dan Double Exponential Smoothing Untuk Meramalkan PDRB di Provinsi NTT

Laura Liokelly Toron¹

¹Laura Liokelly Toron, Institut Sains & Teknologi AKPRIND Email: [email protected]

Yudi Setyawan^2§, ²Yudi Setyawan, Institut Sains & Teknologi AKPRIND Email: [email protected]

Noviana Pratiwi³

³Noviana Pratiwi, Institut Sains & Teknologi AKPRIND Email: [email protected]

^§Corresponding Author

Abstract: Gross Regional Domestic Product is the total number of goods and services produced by production units of all economic sectors of a particular region during one year. BPS NTT noted that the economic growth rate of NTT in 2020 experienced a contraction of -0.83% from 5.24% in the previous year, so this study aims to predict NTT's GRDP using the ELM method and Holt's Double Exponential Smoothing. ELM is an artificial neural network that has one hidden layer that is applied through training and testing process, then involves a binary sigmoid activation function and a Moore Penrose Pseudo Inverse matrix to get the output weight used to predict. DES Holt is a forecasting method that pays attention to trend data plots and uses two parameters in its calculations. The results of the forecasting research show that the ELM method with a proportion of 80%:20% is the best method for predicting the GRDP of NTT. The ELM method produces quarterly GRDP values in 2021, which are 17493.19754, 18154.80753, 18712.02153, and 18822.97416 (billion rupiah) with 4 input neurons, 12 hidden layer neurons, 1 output neuron and the MAPE value is 0.7968% which is smaller than DES Holt.

Keywords: Gross Regional Domestic Product, Extreme Learning Machine, Double Exponential Smoothing Holt.

Abstrak: Produk Domestik Regional Bruto merupakan jumlah total produk barang dan jasa yang dihasilkan unit produksi seluruh sektor perekonomian suatu daerah tertentu selama satu tahun. BPS NTT mencatat bahwa laju pertumbuhan ekonomi NTT tahun 2020 mengalami kontraksi sebesar -0,83% dari tahun sebelumnya 5,24%, sehingga penelitian ini bertujuan meramalkan PDRB NTT menggunakan metode ELM dan Double Exponential Smoothing dari Holt. ELM merupakan jaringan syaraf tiruan

yang memiliki satu hidden layer yang diterapkan melalui proses training dan testing, kemudian melibatkan fungsi aktivasi sigmoid biner dan matriks Moore Penrose Pseudo Inverse untuk mendapatkan output weight yang digunakan untuk meramalkan. DES Holt merupakan metode peramalan yang memperhatikan plot data trend dan menggunakan dua parameter dalam perhitungannya. Hasil penelitian peramalan menunjukkan bahwa metode ELM dengan proporsi 80%:20% adalah metode terbaik dalam meramalkan PDRB NTT. Metode ELM menghasilkan nilai PDRB triwulan pada tahun 2021, yaitu sebesar 17493.19754, 18154.80753, 18712.02153, dan 18822.97416 (miliar rupiah) dengan 4 neuron input, 12 neuron hidden layer, 1 neuron output dan diperoleh nilai MAPE sebesar 0,7968% yang lebih kecil daripada DES Holt.

Kata Kunci: Produk Domestik Regional Bruto, Extreme Learning Machine, Double Exponential Smoothing Holt

• 1.    Pendahuluan

Produk Domestik Regional Bruto (PDRB) yakni total produk barang dan jasa dari seluruh sektor perekonomian suatu daerah tertentu selama satu tahun, merupakan indikator kinerja perekonomian yang akan menjadi bahan evaluasi bagi daerah dalam menyusun kebijakan dan perencanaan pembangunan daerah. Nusa Tenggara Timur (NTT) adalah salah satu provinsi pada bagian timur Indonesia yang memiliki 22 kabupaten dengan 3 pulau utama, yaitu Flores, Timor, dan Sumba. Menurut data BPS provinsi NTT, laju pertumbuhan NTT pada tahun 2020 mengalami kontraksi sebesar -0,83% dari tahun sebelumnya (2019) sebesar 5,24%. Ketidakpastian berakhirnya COVID-19 dan adanya dengan penyebaran virus hewan African Swine Fever (ASF) di sebagian besar wilayah NTT yang mengandalkan industri peternakan sebagai salah satu pencaharian warga, tanpa disadari sewaktu-waktu dapat mengakibatkan kasus kemiskinan semakin meningkat yang berdampak pada penurunan pertumbuhan ekonomi masyarakat di daerah tersebut. Menanggapi situasi yang tidak pasti dan permasalahan perekonomian NTT, maka perlu dilakukan penelitian untuk meramalkan PDRB.

Peramalan atau forecasting adalah suatu aktivitas dalam memprediksi hal yang akan terjadi pada masa yang akan datang dengan memanfaatkan data historis. Perkembangan teknik dan metode dalam peramalan tidak jarang membuat banyak penelitian yang membandingkan metode klasik dan kontemporer untuk menghasilkan nilai peramalan terbaik, sekaligus membuktikan bahwa penggunaan metode terbaru lebih baik dibandingkan metode lama (klasik). Oleh sebab itu, penelitian ini menggunakan metode Double Exponential Smoothing dan Extreme Learning Machine (ELM) untuk meramalkan PDRB NTT pada tahun 2021. Double Exponential Smoothing dari Holt merupakan metode peramalan klasik yang memperhatikan plot data trend dan mengabaikan pola musiman dengan menggunakan dua parameter, yaitu α dan β dalam perhitungannya (Makridakis, 1999). ELM merupakan salah satu jenis metode kontemporer jaringan syaraf tiruan (JST) yang dikenal dengan Single Layer

Feedforward Neural Networks (SLFNs) yang menggunakan satu hidden layer (Huang, Zhu, & Siew, Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks, 2006).

ELM dapat melakukan pembelajaran berdasarkan parameter input weight dan bias yang dibangkitkan secara random dengan fungsi aktivasi yang mentransformasi data output ke dalam suatu rentangan nilai tertentu, sehingga memiliki kelebihan dalam proses learning speed dan mampu menghasilkan nilai error yang sangat kecil (Huang, Zhu, & Siew, 2006). Menurut (Kurniasih, Furqon, & Adinugroho, 2020) pembagian data training yang lebih besar dari data testing akan menghasilkan model prediksi yang lebih baik. Selain itu, jumlah hidden neuron dan proporsi data training dan testing yang optimal pada jaringan ELM akan menghasilkan nilai kesalahan peramalan yang kecil (Alfiyatin, Mahmudy, Ananda, & Anggodo, 2019). Penelitian menggunakan Double Exponential Smoothing dari Holt untuk meramalkan PDRB pernah dilakukan oleh (Martua, 2018). Selanjutnya, penelitian yang membandingkan metode Double Exponential Smoothing dan Extreme Learning Machine (ELM) belum pernah dilakukan sebelumnya, namun ada sebuah penelitian oleh (Dewi, 2018) yang membandingkan metode Holt Winter's Exponential Smoothing dan Extreme Learning Machine (ELM) pada peramalan penjualan semen.

Berdasarkan penjelasan yang telah disampaikan, maka peneliti melakukan peramalan PDRB NTT menggunakan metode Double Exponential Smoothing dari Holt dan metode Extreme Learning Machine (ELM). Kemudian membandingkan hasil peramalan kedua metode tersebut berdasarkan nilai MAPE. Metode dengan nilai MAPE terkecil akan dipilih menjadi model prediksi terbaik dalam meramalkan PDRB NTT di empat triwulan pada tahun 2021.

• 2.    Metode
  
  2.1    Jenis Penelitian

Jenis penelitian yang digunakan adalah penelitian eksploratif, yaitu pendekatan penelitian yang dilakukan untuk menggali atau memperdalam suatu ilmu pengetahuan dan mencari ide-ide baru mengenai suatu permasalahan yang sedang terjadi.

• 2.2    Sumber Data

Penelitian ini menggunakan data sekunder PDRB NTT yang diperoleh dari website Badan Pusat Statistik (BPS) Nusa Tenggara Timur, yaitu https://ntt.bps.go.id.

• 2.3    Lokasi Penelitian

Lokasi penelitian yang digunakan dalam penelitian ini berada di Provinsi Nusa Tenggara Timur.

• 2.4    Metode Pengumpulan Data

Teknik pengumpulan data pada penelitian ini menggunakan data sekunder, yaitu data yang diperoleh dari publikasi informasi atau dokumen yang dipublikasikan oleh Badan Pusat Statistik (BPS) Nusa Tenggara Timur secara berkala.

• 2.5    Variabel Penelitian

Penelitian ini menggunakan satu variabel data times series, yaitu 44 data PDRB harga konstan dari triwulan-I 2010 sampai dengan triwulan-IV 2020 masing-masing dalam satuan miliar rupiah.

• 2.6    Tahapan Analisis Data

• a)    Double Exponential Smoothing Holt

Tahapan analisis data metode Double Exponential Smoothing Holt adalah:

• 1.    Mengumpulkan data historikal berdasarkan kebutuhan penelitian.

• 2.    Mengidentifikasi pola data trend pada data penelitian.

  3.

  
  

Melakukan inisialisasi awal pada data penelitian, yaitu mencari nilai S₁ dan b₁

menggunakan persamaan:

S₁ =X₁

(1)

(2)

,    ^(X2 ^{- X}1) ^{+ (X}4 - ^X3)

= ---------------

Keterangan:

S₁  : pemulusan standar periode ke-1

X₁  : data aktual pada waktu ke-1

b₁  : nilai trend periode ke-1

• 4.    Menentukan parameter pemulusan α dan parameter ^ dengan cara trial and error menggunakan persamaan:

S_t = αX_t + (1-α)(S_t-₁+b_t-₁).                     (3)

b_t=β(S_t-S_t-Λ + (1-β)b_t-1.                    (4)

Keterangan:

S_t  : pemulusan standar periode ke-1

S_t-1: pemulusan standar periode ke t-1

X_t : data aktual pada waktu ke-1 b_t : nilai trend periode ke-1 b_t-1: nilai trend periode ke t-1 a  : parameter pemulusan standar

β  : parameter pemulusan trend linear

• 5.    Menghitung nilai peramalan F_t+m menggunakan persamaan:

Ft+_m =St + bt*m.                       ⁽⁵⁾

Keterangan:

F_t+m: pemulusan standar periode ke-1

S_t  : pemulusan standar periode ke-1

b_t  : nilai trend periode ke-1

m : banyak periode yang diramalkan

• 6.    Menghitung nilai akurasi peramalan MAPE menggunakan persamaan:

_mape = ∑=W±               (6)

n

Keterangan:

• n : jumlah periode waktu data

PE_i : persentase kesalahan

• b)    Extreme Learning Machine (ELM)

Tahapan analisis data metode ELM adalah:

• 1.    Mengumpulkan data historikal berdasarkan kebutuhan penelitian.

• 2.    Melakukan normalisasi data menggunakan persamaan:

0,8 * (X ^- Xmin)   _{n λ}

(7)

X =   -------------r- + 0,1.

^(Xmax   ^xmin)

Keterangan:

• x'  : data hasil normalisasi

• x   : data aktual

• x_mi_n: data aktual minimum

X_max: data aktual maksimal

• 3.    Membagi data menjadi data training dan testing dengan berbagai pilihan

proporsi.

4. Melakukan proses training data untuk mendapatkan bobot output dengan tahapan sebagai berikut:

> Memberikan nilai bias dan bobot input secara random.

> Menghitung nilai output hidden layer (Hi_ni_t) menggunakan persamaan:

Hinit = X.W +b.                             (8) Γ (X1W1 + b1)  -  (X1Wm + bm)l Hinit =         ⋮           ×           ⋮         .                      (9) L (XNWi + bi)  -  (XNWm + bm)l

Keterangan:

Hi∏i_t: matriks untuk output hidden neuron

X : nilai input

W : matriks bobot

b : bias matriks

N : banyaknnya data

m : jumlah node hidden neuron

> Menghitung nilai output hidden neuron (H) menggunakan fungsi aktivasi

untuk masuk ke proses perhitungan matriks Moore-Penrose Pseudo

Inverse menggunakan persamaan:

1

(10)

(11)

H = -—-—-.

⁽¹ + exp ^(-Hi_nit)

g(X₁W₁ + b₁)  -  g(X₁W_m +b

.g(XNW1 + b1)  -  g(X_NWm +b

Keterangan:

H  : hasil output hidden neuron

X   : nilai input

W  : matriks bobot

b   : bias matriks

N  : banyaknnya data

m  : jumlah node hidden neuron

g(X₁ W₁ + b₁) : fungsi sigmoid dari H_init

• > Menghitung matriks Moore-Penrose Pseudo Inverse (H⁺) dari hasil

output hidden neuron (H) dengan fungsi aktivasi menggunakan

persamaan:

H⁺ = (H^tH)^-1 H^t.                            (12)

Keterangan:

H⁺ : matriks Moore-Penrose Pseudo Inverse

H^t : hasil transpose matriks H

(H^tH)^-1  : matriks invers pekalian dari H transpose dan H

• 5.    Menghitung nilai bobot akhir dari hidden layer (β) menggunakan persamaan:

β = H⁺T.                               (13)

Keterangan:

• β   : matriks bobot output

• H⁺ : matriks Moore-Penrose Pseudo Inverse

• T   : matriks target

• 6.    Melakukan proses testing dengan tahapan sebagai berikut:

• >    Menginisiasi nilai bobot input (W) dan bias dari nilai pada proses data training.

• >    Menghitung nilai dari matriks Hi_ni_t menggunakan persamaan:

H_init =X. W + bias.(14)

Γ (X1W1 + b1)  -  (X1Wm +b

Hinit = I       ⋮          ×           ⋮(15)

L (XNW1 + b1)  -  (XNWm +b

Keterangan:

Hinit: matriks untuk output hidden neuron

X W b

N m

>

: nilai input

: matriks bobot

: bias matriks

: banyaknnya data

: jumlah node hidden neuron

Menghitung matriks output hidden layer (H) menggunakan persamaan:

1

"=[

H =-----——-.

^{(1 +} e^χp ^(-Hinit⁾ g(X1W1 + b1)  -  g(XιWm + bm)

^g(X_N^W1 + b₁)  ■••  g(X_NW_m + b_m)

I

(16)

(17)

Keterangan:

H X W b N m

: hasil output hidden neuron

: nilai input

: matriks bobot

: bias matriks

: banyaknnya data

: jumlah node hidden neuron

g(X₁ W₁ + b₁) : fungsi sigmoid dari H_init

> Perhitungan nilai prediksi (Y) menggunakan persamaan: Y = H*β.

(18)

Keterangan:

A Y

H β >

: nilai prediksi yang ternormalisasi

: hasil output hidden neuron

: matriks bobot output

Menghitung nilai MAPE menggunakan persamaan:

∑n~ι∣pE_i∣

MAPE = ==¹—-n

■

(19)

Keterangan:

n : jumlah periode waktu data

PE_i : persentase kesalahan

7. Melakukan denormalisasi data menggunakan persamaan:

_ ((X' - 0,1) * (Xm_ax 0,8

-

Xmin)') _{l v}

^{+ X}min^.

(20)

Keterangan:

x'

x

: data hasil normalisasi

: data hasil denormalisasi

x_mi_n: data aktual minimum

^xmax: data aktual maksimal

• 3.    Hasil dan Pembahasan
  
  3.1    Analisis Statistik Deskriptif Data

Analisis statistis deskriptif data triwulan PDRB NTT tampak pada Tabel 1 berikut.

Tabel 1. Analisis Deskriptif PDRB NTT

Statistik Deskriptif Data PDRB NTT (Miliar Rupiah)
Rata-rata	Minimum	Maksimum	Standar Deviasi
14271,66259	10273,68771	18154,26574	2236,115864

Sumber: BPS NTT, data diolah (2021)

Tabel.1 menunjukkan bahwa rata-rata PDRB NTT secara triwulan dari tahun 2010 hingga 2020 adalah 14271,66259, dengan nilai PDRB terendah sebesar 10273,68771, dan nilai PDRB tertinggi sebesar 18154,26574, serta nilai standar deviasi PDRB sebesar 2236,115864 masing-masing dalam satuan miliar rupiah.

• 3.2    Double Exponential Smoothing Holt

  • 3.2.1    Analisis Pola Data PDRB NTT

Analisis pola data PDRB menggunakan grafik pada MS Excel dan diperoleh hasil seperti pada Gambar 1. berikut.

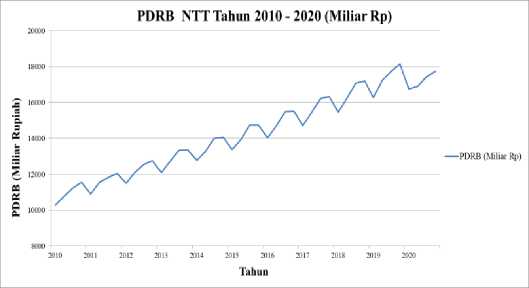
Gambar 1. Analisis pola trend data PDRB NTT Sumber: ntt.bps.go.id

Gambar 1. menunjukkan bahwa terdapat pola data trend untuk data PDRB Provinsi NTT, sehingga penggunaan metode Double Exponential Smoothing Holt sangat disarankan.

• 3.2.2    Parameter α dan ^

Parameter α dan β dihitung dengan melakukan inisialisasi nilai awal, dimana S₁ = X₁, sehingga nilai awal pemulusan S₁= 10273,68771 dan nilai awal untuk pemulusan trend adalah b₁ = 485,99289 masing-masing dalam satuan miliar rupiah. Pengujian parameter dengan nilai α dan ^ mulai dari 0,1 sampai 0,9 menghasilkan nilai akurasi MAPE pada Tabel.2 dan Tabel.3 berikut. Selanjutnya parameter terpilih α = 0,9 dan ^ = 0,1 diuji pada program Data solver MS Excel untuk memperoleh nilai α dan ^ baru yang akan meminimalisir nilai MAPE. Dengan perintah Solver diperoleh nilai parameter untuk meramalkan PDRB adalah sebesar α = 0,61 dan β = 0,07, karena dengan parameter tersebut, nilai galat yang dihasilkan paling kecil, yaitu 0,029372.

Tabel 2. Nilai MAPE Parameter α

α	MAPE
0,1	0,0975464
0,2	0,056177638
0,3	0,044597996
0,4	0,041905335
0,5	0,040662232
0,6	0,040040945
0,7	0,039617561
0,8	0,039145507
0,9	0,038526416

Tabel 3. Nilai MAPE Parameter β

β	MAPE
0,1	0,033642508
0,2	0,035622092
0,3	0,038137237
0,4	0,040726929
0,5	0,043273634
0,6	0,045721158
0,7	0,048053802
0,8	0,049988708
0,9	0,051492798

• 3.2.3    Nilai Peramalan PDRB NTT

Berdasarkan nilai parameter optimal sebesar α = 0,61 dan β = 0,07, maka diperoleh nilai peramalan PDRB NTT pada empat triwulan pada tahun 2021 pada Tabel 4 berikut.

Tabel 4. Nilai Peramalan PDRB NTT

Nilai Ramalan PDRB Tahun 2021 (Miliar Rupiah)
Triw-I	Triw-II	Triw-III	Triw-IV
17816,753030	17979,051097	18141,349170	18303,664724

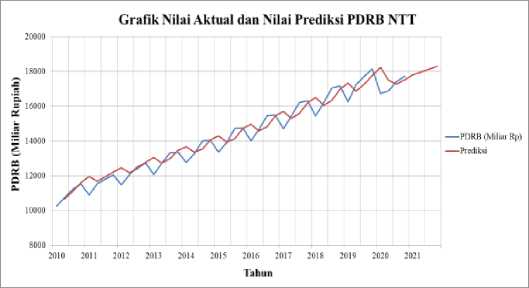
Gambar 2. Grafik nilai aktual dan nilai prediksi PDRB NTT

Berdasarkan Gambar 2, terdapat perbedaan data aktual PDRB NTT dan data prediksinya, dimana ramalan PDRB untuk triwulan I sampai triwulan IV di tahun 2021 menggunakan metode DES Holt mengalami peningkatan, seperti terlihat pada ujung grafik PDRB prediksi yang bergerak naik.

• 3.3    Extreme Learning Machine (ELM)

  • 3.3.1    Normalisasi Data

Hasil dari perhitungan normalisasi data PDRB NTT tahun 2010-2020 dapat dilihat pada Tabel 5 berikut.

Tabel 5. Hasil Normalisasi Data PDRB NTT

No.	Tahun	Triwulan	PDRB (Miliar Rp)	Normalisasi Data
1	2010	1	10273,68771	0,1
2	2010	2	10759,68061	0,149335762
3	2010	3	11251,41098	0,199253965
⋮	⋮	⋮	⋮	⋮
40	2019	4	18154,26574	0,9
41	2020	1	16747,59505	0,757201268
42	2020	2	16897,95530	0,772465148
43	2020	3	17419,70949	0,825431231
44	2020	4	17741,40543	0,858088322

Tabel 5 menunjukkan bahwa data PDRB berada dalam interval [0,1, 0,9], dimana nilai minimum menjadi 0,1 (batas bawah) dan nilai maksimum menjadi 0,9 (batas atas).

• 3.3.2    Pembagian dan Proses Training dan Testing Data

Pembagian data PDRB menggunakan rasio 80%:20% sebagai proses untuk menentukan jumlah neuron hidden layer dan perulangan yang optimal. Dengan 3-20 hidden neuron dan 15, 18, dan 20 perulangan pada proses ELM, maka diperoleh Tabel 6 nilai akurasi MSE berikut.

Tabel 6. Nilai MSE Hasil Pengujian Hidden Neuron dan Perulangannya

Hidden Neuron	Perulangan			Hidden Neuron	Perulangan
	15	18	20		15	18	20
3	0.000546	0.000471	0.000449	12	0.000053	0.000048	0.000045
4	0.000233	0.000255	0.000277	13	0.000053	0.000052	0.000050
5	0.000120	0.000108	0.000171	14	0.000048	0.000047	0.000050
6	0.000095	0.000070	0.000080	15	0.000053	0.000048	0.000049
7	0.000047	0.000072	0.000079	16	0.000050	0.000053	0.000055
8	0.000053	0.000058	0.000053	17	0.000057	0.000052	0.000051
9	0.000056	0.000052	0.000061	18	0.000052	0.000050	0.000052
10	0.000049	0.000062	0.000047	19	0.000051	0.000053	0.000055
11	0.000050	0.000050	0.000054	20	0.000050	0.000053	0.000054

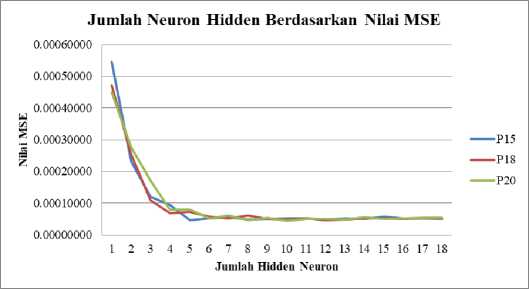
Gambar 3. Grafik jumlah neuron hidden layer terhadap nilai MSE

Tabel 6. menunjukkan bahwa dengan 12 hidden neuron dan perulangan sebanyak 20 akan menghasilkan nilai MSE terkecil, sebesar 0,0000446. Selanjutnya Gambar.3 menunjukkan bahwa semakin banyak jumlah neuron hidden layer, maka kurva nilai MSE akan semakin melandai, yang artinya semakin banyak jumlah neuron hidden layer, maka nilai MSE semakin kecil. Namun, hasil pada Tabel 7 membuktikan bahwa tidak selalu demikian. Hal tersebut dibuktikan dalam penelitian ini, bahwa jumlah neuron hidden layer yang menghasilkan MSE terkecil adalah sebanyak 12 dengan 20 perulangan. Setelah diperoleh 12 hidden neuron optimal, maka selanjutnya menguji

proporsi pembagian data berdasarkan nilai MSE terkecil dan diperoleh hasil proporsi optimal pada Tabel.7 berikut.

Tabel 7. Proporsi Data Training dan Testing Berdasarkan Nilai MSE

Presentase	Pembagian		Nilai MSE
	Data Training	Data Testing
61% : 39%	27	17	0,000058
68% : 32%	30	14	0,00005
75% : 25%	33	11	0,00006
80% : 20%	35	9	0,000047
91% : 9%	40	4	0,00007

Tabel 7 menyimpulkan bahwa pengujian proporsi data training dan testing terbaik adalah sebesar 80%:20% yang menghasilkan nilai MSE terkecil, yaitu 0,000047.

• 3.3.3    Nilai Peramalan PDRB NTT

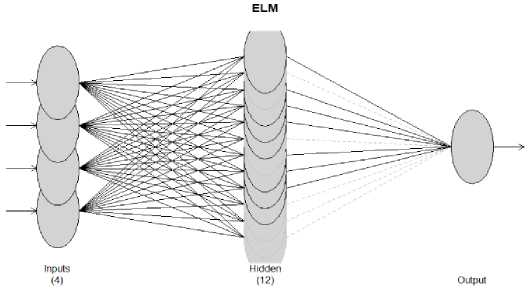
Gambar 4. Arsitektur jaringan syaraf elm data PDRB NTT.

Gambar 4 merupakan arsitektur dari jaringan syaraf data PDRB NTT berdasarkan jumlah neuron input sebanyak 4, jumlah neuron hidden layer sebanyak 12, dan jumlah neuron output sebanyak 1 sebagai hasil dari peramalan PDRB.

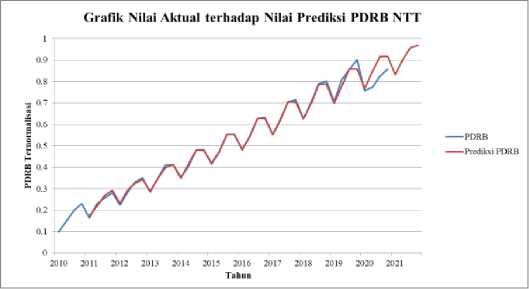
Gambar 5. Grafik data aktual dan data hasil prediksi PDRB NTT.

Gambar 5 memperlihatkan grafik yang mirip pada tahun 2010 sampai 2018 dan terlihat perbedaan yang cukup jelas pada tahun-tahun setelahnya. Hal ini disebabkan oleh nilai error yang terjadi dari data aktual terhadap data hasil prediksi data PDRB, dan dapat dilihat bahwa PDRB mengalami peningkatan pada tahun 2021 dengan nilai peramalan ternormalisasi pada Tabel 8 berikut.

Tabel 8. Hasil Prediksi PDRB NTT Pertriwulan Tahun 2021

Tahun	Prediksi Triwulan Ternormalisasi
2021	1         0,8328914 2         0,900055 3        0,9566208 4        0,9678842

• 3.3.4    Denormalisasi Data

Setelah memperoleh nilai peramalan, selanjutnya dilakukan denormalisasi data PDRB hasil peramalan yang tampak pada Tabel 9.

Tabel 9. Data Prediksi PDRB NTT Denormalisasi.

Tahun	Triwulan	Prediksi Ternormalisasi	Prediksi Denormalisasi
2021	1	0,8328914	17493,19754
	2	0,900055	18154,80753
	3	0,9566208	18712,02153
	4	0,9678842	18822,97416

• 3.4    Pengukuran Akurasi MAPE

Berdasarkan parameter, jumlah hidden neuron, dan proporsi data training dan testing yang optimal, maka diperoleh MAPE pada Tabel 10.

Tabel 10. Perbandingan Nilai MAPE.

Metode	Nilai MAPE (%)
Double Exponential Smoothing Holt (α=0,61 dan ^ = 0,07)	2,9372
Extreme Learning Machine	0,7968

Tabel 10 menunjukkan bahwa ELM menjadi metode terbaik dalam meramalkan PDRB NTT, karena nilai MAPE yang kecil, yaitu 0,7968%. Secara statistika, proses ELM melibatkan perulangan pembelajaran hingga memperoleh MAPE terkecil. Perulangan tersebut apabila dilakukan secara terus menerus, maka terbentuk sejumlah data sampel pengujian MAPE, sehingga dapat dihitung interval keyakinan untuk

meramalkan MAPE. Penelitian ini kemudian melakukan 30 kali perulangan untuk mendapat MAPE sebanyak perulangannya, dan diperoleh rata-rata MAPE = 0,007907854 dengan standar deviasi sebesar 0,000396298, sehingga interval keyakinan untuk meramalkan MAPE dengan tingkat keyakinan 95% adalah:

σ

σ

X — Za/^.— < μ < X + Za/^.— 0,000396298                         0,000396298

0,007907854 — 1,96 *----=---<μ< 0,007907854 + 1,96 *----=---

√30                               √30

0,00776604 < μ < 0,008049667

Dengan demikian, dapat disimpulkan bahwa pada tingkat keyakinan 95%, rata-rata nilai MAPE dengan 30 kali perulangan adalah berkisar antara 0,00776604 - 0,008049667.

• 4.    Kesimpulan

Berdasarkan hasil analisis dan pembahasan, diperoleh beberapa disimpulkan sebagai berikut:

• 1.    Analisis deskriptif menunjukkan bahwa rata-rata PDRB NTT adalah 14271,66259, dengan nilai PDRB terendah sebesar 10273,688, dan nilai PDRB tertinggi sebesar 18154,266, serta nilai standar deviasi PDRB sebesar 2236,115864 dalam satuan miliar rupiah.

• 2.    Parameter terbaik dalam meramalkan PDRB NTT menggunakan metode Double Exponential Smoothing Holt adalah α=0,61 dan β=0,07 dan nilai ramalan triwulan I sampai IV tahun 2021 adalah sebesar 17816,75303, 17979,051097, 18141,34917, dan 18303,664724 (satuan miliar rupiah).

• 3.    Berdasarkan proporsi 80% data training dan 20% data testing dengan 4 neuron input, 12 hidden neuron, dan 20 perulangan pada metode ELM, diperoleh nilai ramalan triwulan I sampai IV tahun 2021 sebesar 17493,19754, 18154,80753, 18712,02153, dan 18822,97416 (satuan miliar rupiah).

• 4.    Berdasarkan perbandingan nilai MAPE terkecil, metode ELM adalah metode terbaik dalam meramalkan PDRB di Provinsi Nusa Tenggara Timur adalah metode ELM dengan nilai MAPE sebesar 0,7968%.

Ucapan Terima Kasih

Dalam penyusunan tulisan ini, banyak pihak telah terlibat dan mendukung selesainya penelitian ini. Oleh sebab itu, dengan segala kerendahan hati, peneliti ingin menyampaikan rasa syukur dan terima kasih kepada Institut Sains & Tekonologi AKPRIND Yogyakarta, khususnya Bapak/ Ibu dosen Jurusan Statistika untuk segala bimbingan dan arahannya.

Daftar Pustaka

Alfiyatin, A. N., Mahmudy, W. F., Ananda, C. F., & Anggodo, Y. P. (2019). Penerapan Extreme Learning Machine (ELM) Untuk Peramalan Laju Inflasi di Indonesia. Jurnal Teknologi Informasi dan Ilmu Komputer (JTIIK), 6(2), 179-186.

Dewi, E. A. (2018). Perbandingan Metode Holt Winter's Exponential Smoothing dan Extreme Learning Machine (ELM) Pada Peramalan Penjualan Semen. Yogyakarta: Universitas Islam Indonesia.

Huang, G.-B., Zhu, Q.-Y., & Siew, C.-K. (2006). Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks. Neurocomputing, 489-501.

Huang, G.-B., Zhu, Q.-Y., & Siew, C.-K. (2006). Extreme Learning Machine: Theory and Applications. Neurocomputing, 70, 489-501.

Kurniasih, I. H., Furqon, M. T., & Adinugroho, S. (2020). Prediksi Pertumbuhan Penduduk di Kota Malang Menggunakan Metode Extreme Learning Machine (ELM). Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer, 4(2), 509-516.

Makridakis. (1999). Metode Dan Aplikasi Peramalan. In Makridakis, Metode Dan Aplikasi Peramalan (p. 101). Jakarta: Binarupa Aksara.

Martua, M. N. (2018). Peramalan Produk Domestik Regional Bruto (PDRB) Sektor Pertanian Kota Padangsidimpuan Tahun 2019. Medan, Sumatera Utara, Indonesia: Universitas Sumatera Utara.

48