Jurnal Matematika Vol. 11, No.1, Juni 2021, pp. 64-74

Article DOI: 10.24843/JMAT.2021.v11.i01.p137

ISSN: 1693-1394

Perbandingan GCV Dan UBR Dalam Regresi Nonparametrik Multivariabel

Luh Putu Safitri Pratiwi

Program Studi Sistem Informasi, Institut Teknologi dan Bisnis Stikom Bali e-mail: putu_safitri@stikom-bali.ac.id

Ni Putu Meina Ayuningsih

Program Studi Sistem Informasi, Institut Teknologi dan Bisnis Stikom Bali e-mail: meina_ayuningsih@stikom-bali.ac.id

Ni Made Dwijayani

Program Studi Sistem Informasi, Institut Teknologi dan Bisnis Stikom Bali e-mail: nimade_dwijayani@stikom-bali.ac.id

Abstract: The spline truncated is a popular and frequently used nonparametric regression model approach. This study aims to determine the optimal knot point using the GCV and UBR methods, which are applied to the Maternal Mortality Rate in Bali Province. The more optimal the knot points selected in making the nonparametric regression model, the greater the goodness of the model obtained. The results showed that the GCV method in terms of choosing the best model criteria for determining the optimal knot point was better than the UBR method. The GCV method produces an MSE value of 0.036 which lies in the three knot linear Spline model, while the UBR method produces an MSE value of 0.074 which is located on the one knot linear Spline model.

Keywords: GCV, UBR, knot point, Spline, nonparametric

Abstrak: Spline truncated merupakan pendekatan model regresi nonparametrik yang popular dan sering digunakan. Penelitian ini bertujuan sebagai penentu titik knot optimal dengan menggunakan metode GCV dan UBR, yang diaplikasikan pada data Angka Kematian Ibu di Provinsi Bali. Semakin optimal titik knot yang dipilih dalam membuat model regresi nonparametrik maka semakin besar pula kebaikan model yang diperoleh. Hasil penelitian menunjukkan bahwa metode GCV dalam hal memilih kriteria model terbaik untuk penentuan titik knot optimal lebih baik dibandingkan metode UBR. Metode GCV menghasilkan nilai MSE sebesar 0,036 terletak pada model Spline linier tiga knot, sedangkan metode UBR menghasilkan nilai MSE sebesar 0,074 yang terletak pada model Spline linier satu knot.

Kata Kunci: GCV, UBR, titik knot, Spline, nonparametric

  • 1.    Pendahuluan

Memilih parameter penghalus sangat diperlukan dalam Spline ketika terdapat error yang independen dengan varian tidak diketahui untuk itu digunakan suatu metode yang disebut dengan Generalized Cross Validation (GCV). Wang (1998) merepresentasikan suatu Spline penghalus dalam suatu model dengan keadaan tertentu dan memperluas metode Unbiased Risk (UBR), Cross Validation (CV), Generalized Maximum Likelihood (GML), serta Generalized Cross Validation (GCV), untuk suatu barisan moving average error. Gu, et al. (1992) melakukan penelitian dengan tujuan untuk memilih parameter penghalus untuk meminimumkan nilai GCV, dimana nilai dari GCV tersebut optimal secara asimtotik untuk meminimumkan Mean Square Error (MSE). Adapun metode lain dalam pemilihan titik knot yang optimal adalah UBR. Metode UBR sering digunakan apabila parameter dari σ2 diketahui (Sari, 2016).

Setiap metode dalam statistika pastinya memiliki kelebihan dan kekurangan. Adapun kelebihan GCV dan UBR dalam memilih titik knot optimal ialah invarian terhadap transformasi dan tidak memerlukan informasi terhadap σ², tak terlepas dari kesederhanaanya dalam menyelesaikan perhitungan sehingga optimal secara asimtotik (Wahba,1990 & Wang 1998). Metode GCV dalam hal pemilihan titik knot lebih baik digunakan jika data Gaussian yang berdistribusi normal, sementara metode UBR lebih baik digunakan pada data non-Gaussian atau tidak berdistribusi normal (Wang, 1998).

Penelitian mengenai pemilihan titik knot terbaik pernah diteliti oleh Pratiwi (2017) mengenai perbandingan metode CV dan GCV. Hasil yang didapat yaitu model terbaik dengan menggunakan metode CV dan menghasilkan nilai minimum sebesar 77,378 pada model Spline linier satu knot. Sari (2016) juga pernah membandingkan metode GCV dan UBR yang menghasilkan R2 adj sebesar 52,15% serta nilai MSE sebesar 0,013 dan nilai-nilai ini merupakan nilai satu titik knot optimum dari GCV. Hal tersebut merupakan bukti bahwa GCV pada data berdistribusi normal lebih baik dibandingkan dengan metode UBR dalam kasus pemilihan knot untuk angka kematian maternal

Penerapan metode ini diaplikasikan pada data Angka Kematian Ibu (AKI). Millenium Development Goals (MDGs) memiliki beberapa tujuan diantaranya mencapai target AKI sebesar 102 per 100.000 kelahiran hidup dan diharapkan bisa turun lagi, akan tetapi menurut data Survei Demografi dan Kesehatan Indonesia (SDKI) tahun 2007 AKI di Indonesia masih cukup tinggi yaitu mencapai 228 per 100.000 kelahiran hidup sedangkan di tahun 2012 tercatat mencapai 359 per 100.000 kelahiran hidup (Kemenkes RI, 2013).

  • 2.    Regresi Nonparametrik Spline

Fungsi Spline diberikan oleh persamaan berikut.

pr

fj (xji ) = Σ βujxβ + Σ β p+k) j (xH - Kkj )+ , J = 1,2,..., h                           (1)

u=0            k=1

merupakan titik-titik knot. Nilai p pada persamaan (1) merupakan derajat dari Spline.

Untuk pemilihan titik knot optimal dalam penelitian ini menggunakan metode GCV dan UBR. Secara umum GCV didefinisikan sebagai berikut.

GCV (K1, K2,..., Kr) =


MSE(K1,K2,...,Kr)

{ n'trace [ I - A( K1, K1,..., Kr )]}2


(2)


dengan:

n

MSE(K1,K2,...,Kr) =1 ∑(yi -yi)2, A(K1,K2,...,Kr) = X(x'x)-1 X', dan I matriks identitas.

n i=1

Seperti halnya GCV, UBR merupakan salah satu metode dalam pemilihan titik knot optimal dalam Spline truncated, yang dirumuskan sebagai berikut.

2 σ2

+--trace

n


U (k ) = 1 ⅛-Α( k)) n’ +


2


[A2 (k)]


dengan:

A(k) = X(X'X)-1 X' dan I matriks identitas.

  • 3.    Hasil dan Pembahasan

    a.    Karakteristik Data AKI dan Faktor Mempengaruhinya

Penelitian ini menggunakan data AKI dan beberapa faktor yang mempengaruhinya pada 57 kecamatan di Provinsi Bali (BPS, 2017). Berikut ini merupakan karakteristik AKI dan beberapa faktor mempengaruhinya dalam Tabel 1.

Tabel 1.Karakteristik Data AKI dan Faktor Mempengaruhinya

Var

Rata-rata

Varians

Minimum

Maximum

y

1,19

0,23

0,30

2,79

X1

98,03

8,64

90,53

102,81

*2

96,69

21,28

76,45

102,53

98,71

4,49

93,92

102,96

*4

92,22

14,71

80,81

98,80

Berdasarkan Tabel 1, diketahui bahwa nilai rata-rata AKI di Provinsi Bali adalah sebesar 1,19 kelahiran hidup. Sementara AKI minimumnya sebesar 0,30 kelahiran hidup sedangkan AKI maksimum mencapai 2,79 kelahiran hidup. Beberapa variabel yang diduga mempengaruhi yaitu persentase persalinan dengan bantuan tenaga medis , persentase ibu hamil memperoleh Tablet Fe1 , persentase ibu hamil melakukan program K1 , persentase ibu hamil melakukan program K4 . Langkah selanjutnya,

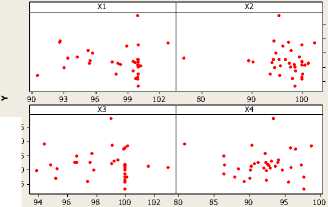
melakukan analisis pola dengan scatter plot, untuk melihat hubungan antara variabel y dengan masing-masing variabel x dapat dilihat pada Gambar 1.

Scatterplot of Y vs X1, X2, X3, X4

90

2.5

2.0

1.5

1.0

0.5

2.5

2.0

1.5

1.0

0.5

Gambar 1. Scatter plot

Gambar 1 menunjukkan bahwa AKI dengan variabel bantuan tenaga medis 0*1), ibu hamil memperoleh Tablet Fe1 (^z), ibu hamil mengikuti program K1 G⅛) , ibu hamil mengikuti program K4 (^4), tidak mengikuti pola tertentu. Jadi pola hubungan antara masing-masing variabel prediktor dengan variabel respon sesuai penggunaannya dengan pendekatan nonparametrik begitupula pemodelannya memakai regresi nonparametrik.

  • b.    Pemodelan AKI Berdasarkan Titik Knot Optimal

Tabel 2 merupakan knot minimun pada GCV dan UBR. Minimum knot pada GCV yaitu di tiga titik knot, sedangkan pada UBR nilai minimum terletak pada satu titik knot hasil ini selanjutnya akan digunakan dalam pemodelan AKI di Provinsi Bali.

Tabel 2. Titik Knot GCV dan UBR minimum

Titik Knot

Nilai GCV Minimum

Nilai UBR Minimum

Satu Knot

0,37331

0,000403

Dua Knot

0,28500

0,000480

Tiga Knot

0,07722

0,000500

  • c.    Pengujian Signifikansi Parameter Model GCV dan UBR

    1)    Pengujian Signifikansi pada GCV

Dalam menguji signifikansi parameter maka akan dilakukan pengujian secara serentak terlebih dahulu. Setelah itu dilanjutkan dengan pengujian signifikansi parameter individu, bila pengujian secara serentak memiliki nilai yang signifikan terhadap AKI.

  • a)    Uji Serentak

Uji hipotesis serentak untuk parameter model sebagai berikut.

H :β = β =...= β = 0

0     11       21              (p+r) h

Hi : minimal ada satu βιιj ≠ 0, u = 1,2,...,(p + r),

dan j = 1,2,..., h.

Tabel 3. Analysis of Variance (ANOVA) Model Regresi Spline Secara

Serentak

Sumber Variansi

df

SS

MS

Fhit

Regresi

53

7,589

0,143

3,97

Error

3

0,108

0,036

Total

56

7,697

-

Tabel 3, dapat diambil keputusan bahwa H0 ditolak karena Fhit=3,97> Fta-bel=3,820, bahwa ada variabel yang berpengaruh nyata terhadap model.

  • b)    Uji Individu

Selanjutnya dilakukan uji parameter secara individu dengan uji t. Hipotesis uji t sebagai berikut:

Ho: βuj= 0

H1: βuj≠ 0

Berikut ini akan ditunjukkan uji signifikansi parameter model regresi secara individu dalam Tabel 4.

Tabel 4.Uji Parameter Model Regresi Secara Individu

Variabel

Parameter

Estimasi

thit

Keputusan

Constant

^

Z^0

0,08

4,94

Signifikan

*1

β11

3,38

5,22

Signifikan

β21

-3,37

-5,22

Signifikan

ˆ

β31

-2,55

-2,83

Signifikan

β41

2,90

3,45

Signifikan

β12

-3,87

-5,85

Signifikan

β22

6,79

5,95

Signifikan

ˆ

β32

-9,41

-6,49

Signifikan

ˆ

β42

6,41

6,61

Signifikan

*3

β13

1,45

4,63

Signifikan

β23

-1,53

-3,58

Signifikan

ˆ

β33

0,46

0,49

Tidak Signifikan

ˆ

β43

0,01

0,02

Tidak Signifikan

*4

ˆ

β14

-1,33

-8,93

Signifikan

β24

1,60

7,95

Signifikan

β34

-0,17

-0,68

Tidak Signifikan

ˆ β44

-0,21

-0,92

Tidak Signifikan

Apabila nilai tthit ∣> t0 025.3, dengan nilai t0 025.3 yaitu sebesar 2,447 maka keputusan yang diambil adalah menolak Ho yang artinya bahwa terdapat pengaruh variabel independen terhadap variabel dependen. Namun, berdasarkan Tabel 4 dari 17 parameter terdapat variabel yang tidak signifikan yaitu variabel x3 pada β3 dan β3, sedangkan di variabel x4 pada β34 dan β44 selain parameter tersebut, parameter yang lainnya memberikan pengaruh yang signifikan terhadap model.

  • 2)    Pengujian Asumsi Error GCV

Pengujian asumsi error berkaitan dengan layak tidaknya suatu model regresi digunakan untuk menggambarkan pola hubungan antar variabel independen dan dependen. Apabila model regresi tersebut melanggar asumsi error maka tidak disarankan dipakai untuk menggambarkan pola hubungan antar variabel walaupun model memenuhi kreteria dan parameternya signifikan

  • a)    Uji Identik

Pengujian identik pada penelitian ini yaitu dengan menggunakan uji Glejser.

Uji Glejser adalah pemodelan yang dilakukan untuk mengetahui ada tidaknya suatu heteroskedastisitas.

Hipotesis untuk uji Glejser:

H : error identik

H : error tidak identik

Tabel 5. ANOVA Uji Glejser

Sumber Variansi

df

SS

MS

Fhit

Regresi

53

0,051

0,002

0,990

Error

3

0,011

0,002

Total

56

0,063

-

Berdasarkan Tabel 5, bahwa nilai statistik uji Fhit=0,990 < Ftabel=3,820, sehingga dapat dikatakan bahwa error identik atau dapat diartikan bahwa tidak terdapat heteroskedastisitas pada data.

  • b)    Uji Independen

Salah satu cara mendeteksi adanya independensi pada error yaitu dengan perhitungan nilai Durbin Watson dimana dhitung =2,419 > dU =1,034 sehingga gagal tolak Ho, yang dapat disimpulkan bahwa asumsi error independen telah terpenuhi.

  • c)    Uji Distribusi Normal

Berdasarkan Tabel Kolmogorov-Smirnov didapatkan nilai D sebesar

0,224. Untuk nilai D = Sup∖Fn(x)-Ffi(x)| yaitu sebesar 0,178. Keputusan x

yang diperoleh yaitu gagal tolak Ho karena D < D0 05.35. Berdasarkan keputusan tersebut maka asumsi telah tercapai dilihat dari nilai error berdistribusi normal.

  • 3)    Pengujian Signifikansi Parameter dengan UBR

Langkah – langkah pengujian signifikansi parameter dimulai dengan melakukan pengujian parameter secara serentak, maka selanjutnya melakukan tahapan uji secara individu, sebagai berikut:

  • a)    Uji Serentak

Uji hipotesis serentak untuk model diberikan oleh:

H : β = β =...= β = 0

0 /11    /21               ( p+r) h

H, : minimal ada satu β,i ≠ 0, 1                                             uj

u = 1,2,..., (p + r), dan j = 1,2,..., h.

Berikut hasil uji estimasi parameter secara serentak dapat dilihat dalam Tabel 6.

Tabel 6. Analysis of Variance (ANOVA) Model Regresi Spline Secara Serentak

Sumber Variansi

df

SS

MS

Fhit

Regresi

53

20,999

0,396

5,35

Error

3

0,222

0,074

Total

56

8,231

-

Berdasarkan Tabel 6, akan dibandingkan nilai dari Fhit dengan Ftabel. Hasil yang diperoleh bahwa nilai Fhit=5,35 > Ftabel=3,820, sehingga H0 ditolak. Dalam artian bahwa minimal ada satu variabel yang memberikan pengaruh yang signifikan terhadap model.

  • b)    Uji Individu

Selanjutnya dilakukan uji parameter secara individu dengan uji t. Hipotesis uji t sebagai berikut:

H0: βu = 0

Hi: βu≠ 0

Tabel 7.Uji Parameter Model Regresi Secara Individu

Variabel

Parameter

Estimasi

thit

Keputusan

Constant

ˆ

β01

0,03

5,94

Signifikan

βii

1,38

6,20

Signifikan

x1

β21

3,40

7,21

Signifikan

β12

2,55

5,83

Signifikan

x2

ˆ

β22

-3,90

5,42

Signifikan

ˆ

β13

4,87

8,81

Signifikan

x3

β23

6,79

8,90

Signifikan

β14

-5,41

5,40

Signifikan

x4

ˆ

β24

7,41

3,60

Signifikan

Apabila nilai ∖thit ∣> t0 025.3 dengan nilai ^0 025 3 sebesar 2,447 maka berdasarkan Tabel 7, sembilan parameter tersebut signifikan. Sehingga secara keseluruhan keempat variabel memberikan pengaruh terhadap model.

  • 4)    Pengujian Asumsi Error UBR

Pengujian asumsi error digunakan untuk melihat apakah error memenuhi kreteria identik, independen, dan berdistribusi normal pada regresi nonparametrik Spline truncated. Berikut akan disajikan hasil uji dari masing-masing asumsi.

  • a)    Uji Identik

Untuk uji asumsi identik dapat dilakukan dengan menggunakan uji Glejser.

Hipotesis untuk uji Glejser:

H : error identik

H : error tidak identik

Tabel 8. ANOVA Uji Glejser

Sumber Variansi

df

SS

MS

Fhit

Regresi

53

0,551

0,01

3,33

Error

3

0,011

0,003

Total

56

0,063

-

Berdasarkan Tabel 8, bahwa nilai statistik uji Fhit=3,33 < Ftabel=3,820, sehingga dapat dikatakan bahwa error identik atau dapat diartikan bahwa tidak terdapat heteroskedastisitas.

  • b)    Uji Independen

Setelah pengujian asumsi error identik, uji asumsi yang harus terpenuhi selanjutnya yaitu error bersifat independen. Asumsi error independen dapat terpenuhi bila adanya independensi pada error. Salah satu cara mendeteksi adanya independensi pada error yaitu dengan perhitungan nilai Durbin Watson dimana dhitung =4,666 > dU =1,034 sehingga gagal tolak Ho, yang dapat disimpulkan bahwa asumsi error independen telah terpenuhi.

  • c)    Uji Distribusi Normal

Berdasarkan Tabel Kolmogorov-Smirnov didapatkan nilai D sebesar

0,224. Sementara itu uji D = Sup F(x)-F0(x)| sebesar 0,178. Keputusan x

yang diperoleh yaitu gagal tolak Ho karena D < D0 05.35 . Berdasarkan keputusan tersebut yang artinya asumsi error berdistribusi normal terpenuhi.

  • 5)    Perbandingan Metode GCV dan Metode UBR dalam Pemodelan Regresi Nonparametrik Spline

Disajikan tabel perbandingan dua buah metode GCV dan UBR untuk data AKI di Provinsi Bali.

Tabel 9. Perbandingan Metode GCV &Metode UBR

Pengujian

GCV

UBR

MSE

0,036

0,074

Asumsi Residual Identik

Terpenuhi

Terpenuhi

Asumsi Residual Independen

Terpenuhi

Terpenuhi

Asumsi Residual Distribusi Normal

Terpenuhi

Terpenuhi

Berdasarkan Tabel 9, perbandingan antara GCV dan UBR dilihat dari nilai MSE masing-masing. Terlihat dari nilai MSE metode GCV lebih kecil dibandingkan metode UBR pada data AKI di Provinsi Bali.

  • 4.    Kesimpulan dan Saran

Aplikasi data AKI menggunakan metode GCV minimum menghasilkan model sebagai berikut

y = 0,08 + 3,38x1 -3,37(x1 -92,79)+ - 2,55(x1 -97,80)+ + 2,90(x1 -98,30)+ +

-3,87x2 + 6,79(x2 -81,24)+ -9,41(x2 -91,89)+ + 6,41(x2 -92,95)+ +

+1,45x3 -1,53(x3 - 95,58)+ + 0,46(x3 - 99,27)+ + 0,01(x3 - 99,64)+ +

-1,33x4 +1,60(x4 - 84,11)+ - 0,17(x4 - 91,46)+ - 0,21(x4 - 92.19)+

Sedangkan, aplikasi data AKI dengan metode UBR minimum sebagai berikut.

y = 0, 03 + 1,38x1 + 3,40(x1 - 98,99)+ + 2,55x2

-3,90(x2 - 82,55)+ + 4,87x3 + 6,79(x3 -94,58)+

- 5,41 x4 + 7,41(x4 - 89,11)+

Model terbaik terletak pada GCV Spline linier tiga titik knot, dengan nilai GCV yaitu sebesar 0,077 dan nilai MSE sebesar 0,036.

Ucapan Terima Kasih

Kami mengucapkan terima kasih kepada ITB STIKOM Bali yang telah memberi dukungan financial terhadap penelitian ini.

Daftar Pustaka

BPS (Badan Pusat Statistik) Propinsi Bali. (2017). Bali Dalam Angka Tahun 2017. Bali : Badan Pusat Statistik.

Gu, C., Heckman, N., and Wahba, G. (1992). “A Note on Generalized Cross Validation with Replicates”. Journal Statistics and Probability Letters 14, Vol : 14 No. 4; 283-287.

Kemenkes RI (Kementerian Kesehatan Republik Indonesia). (2013). Profil Kesehatan Indonesia Tahun 2012. Jakarta: Kementerian Kesehatan RI.

Padilah, T. N., & Adam, R. I. (2019). “Analisis Regresi Linier Berganda Dalam Estimasi Produktivitas Tanaman Padi Di Kabupaten Karawang”. Jurnal fibonacci. Jurnal Pendidikan Vol. 5(2), pp: 117-128

Pratiwi,L, P, S. (2017). “Perbandingan Metode Cross Validation Dan Generalized Cross Validation Dalam Regresi Nonparametrik Birespon Spline”. Jurnal Varian Vol.1(1).

Sari, S. U. R. (2016). Perbandingan Model Regresi Nonparametrik Spline Multivariabel Dengan Menggunakan Metode Generalized Cross Validation (Gcv) Dan Unbi-

assed Risk (Ubr) Dalam Pemilihan Titik Knot Optimal. Tesis. Jurusan Statistika, FMIPA, Institut Teknologi Sepuluh Nopember (ITS), Surabaya

Wahba, G. (1990). “Spline Models for Observation Data, SIAM, Philadelphia”.

CBMSNSF Regional Conference Series in Applied Mathematics. Vol. 59

Wang, Y. (1998). “Smoothing Spline Models With Correlated Random Errors”. Journal of The American Statistical Association. Vol. 93. No. 441. Hal. 341-348

74