Optimasi Radio Frequency Unit Berbasis Interferensi Kanal Menggunakan Pendekatan Upper Bound Bilangan Kromatik
on
Jurnal Matematika Vol. 3 No. 1, Juli 2013. ISSN : 1693-1394
Optimasi Radio Frequency Unit Berbasis Interferensi Kanal Menggunakan Pendekatan Upper Bound Bilangan Kromatik
Noor Saif Muhammad Mussafi
Program Studi Matematika Fakultas Sains dan Teknologi UIN Sunan Kalijaga Jl. Marsda Adisucipto No. 1 Yogyakarta 55281 e-mail: om norsa@yahoo.com
Abstrak: Gangguan gelombang transmisi radio sering terjadi dikarenakan kesenjangan antara bandwith frekuensi yang tersedia dan tingginya permintaan frekuensi. Telaah pewarnaan graf khususnya algoritma Welsh-Powell diharapkan dapat memberikan alternatif solusi permasalahan tersebut. Penelitian ini mengkaji optimasi radio frequency unit berbasis interferensi kanal menggunakan pendekatan upper bound bilangan kromatik. Data mengenai persebaran radio akan direpresentasikan dalam bentuk graf dengan mempertimbangkan tingkat interferensi yaitu kuat medan listrik, selanjutnya akan dianalisis menggunakanpewarnaan graf dengan algoritma Welsh-Powell. Hasil penelitian memberikan alternatif model distribusi frekuensi radio yang optimal.
Keywords: Radio Frequency Unit, Interferensi, Algoritma Welsh-Powell.
-
1. Pendahuluan
Gangguan gelombang transmisi radio kerap kali menyebabkan suara menjadi tidak jelas sehingga membuat masyarakat khususnya penggemar media radio menjadi tidak nyaman. Gangguan gelombang atau sering disebut interferensi terjadi akibat dua gelombang atau lebih yang saling berpadu atau bersuposisi sehingga menghasilkan pola interferensi maksimum dan minimum.Dengan bertambahnya penggunaan telepon seluler, gelombang wi-fi, dan berbagai aplikasi lain terhadap gelombang serta terbatasnya jumlah frekuensi yang tersedia tentunya menambah deretan persolan yang perlu ditangani untuk menjaga stabilitas komunikasi. Karena semakin banyak pengguna yang memanfaatkan frekuensi gelombang radio ini maka perlu adanya regulasi atau pengaturan agar tidak terjadi interferensi antara radio satu dengan yang lain.
Menurut peraturan Menteri Komunikasi dan Informasi No. 13/PER/M. KOMINFO /08/2010, setiap wilayah telah diatur pembagian masing-masing frekuensinya. Pengaturan frekuensi radio FM (frequency modulation) Daerah Istimewa Yogyakarta dilaksanakan sesuai dengan keputusan Menteri Perhubungan KM No. 15 Tahun 2003 yang menyebutkan bahwa rentang pita frekuensi radio yang digunakan adalah 87,6 MHz-107.9 MHz. Provinsi Daerah Istimewa Yogyakartamendapat alokasi frekuensi sebanyak 42 kanal FM. Kanal-kanal tersebut masing-masing 14 kanal untuk Kota Yogyakarta, 17 kanal untuk Sleman, 4 kanal untuk Bantul, 3 kanal untuk Gunung Kidul dan 3 kanal untuk Kulon Progo. Agar tidak terjadi interferensi, maka dalam pengaturan kanal perlu mempertimbangkan beberapa aspek salah satu diantaranya yaitu kuat medan listrik.
Untuk itu pertanyaan terbuka yang muncul adalah bagaimana mengoptimalkan pengaturan kanal radio dan pendekatan apa yang dapat digunakan. Oleh karena itu penelitian ini mengembangkan konsep pewarnaan graf heuristik yang merupakan sub kajian dari teori graf menggunakan pendekatan upper bound greedy algorithm untuk mengoptimalkan layanan publik dengan mempertimbangkan kuat medan listrik.
-
2. Tinjauan Pustaka
-
2.1. Graf
-
Menurut Winston (1990), suatu Graf G terdiri dari himpunan tidak kosong yang dise-
but titik V (G) dan himpunan pasangan tidak terurut dari titik-titik tersebut yang dina-
V (2G)
makan sisi E (G) ⊆
Dua sisi atau lebih yang menghubungkan satu pasang titik
disebut sisi rangkap (multiple edges). Suatu sisi yang titik ujungnya sama disebut loop.
Graf tanpa sisi rangkap dan tanpa loop disebut graf sederhana (simple graph). Jika diketahui graf G = (V, E) dengan V(G) = {a, b, c, d, e, f} dan E(G) = {aa, ab, ac, ae, cd, cf},
maka graf tersebut dapat dinyatakan seperti berikut.

Gambar 1. Graf G
Graf pada gambar 1 tidak sederhana karena mengandung loop. Derajat suatu titik v di G, dinyatakan dengan d(v), adalah cacah sisi di G yang terkait dengan v dengan masing-masing loop dihitung sebagai dua sisi yang terkait dengan v . Untuk graf pada gambar 1, d(a) = 5, d(b) = 2, d(c) = 5, d(d) = 1, d(e) = 2, dan d(f) = 1 dan jumlah dera jat titik di G adalah 16. Graf berarah (directed graf) D = (V, A) adalah graf yang setiap sisinya diberikan orientasi arah yang dikenal dengan arcs seperti pada gambar 2.a, (u, v) dan (v, u) menyatakan dua buah sisi yang berbeda, dengan kata lain (u,v) = (v,u )•

Gambar 2. (a) Graf berarah (b) Graf lengkap K4
Graf planar adalah graf yang dapat digambarkan pada bidang datar sedemikian sehingga tidak ada sisi-sisinya yang saling berpotongan (bersilangan). Graf lengkap K4 adalah graf planar (lihat gambar 2.b)
-
2.2. Pewarnaan Graf
-
2.2.1. Pewarnaan Titik
-
Misalkan G graf tanpa loop. Suatu pewarnaan-k (pewarnaan titik) untuk graf Gadalah pengguanaan sebagian atau semua k warna berbeda untuk mewarnai semua titik di G sehingga setiap dua titik yang terhubung langsung diberi warna berbeda. Jika G mempunyai pewarnaan-k maka G dikatakan dapat diwarnai dengan k warna.
Bilangan kromatik (chromatic number) dari graf G, dinyatakan dengan χ(G) adalah bilangan k terkecil sehingga G dapat diwarnai dengan k warna. Warna-warna yang digunakan untuk mewarnai dapat dinyatakan dengan bilangan 1, 2, 3, . . . , k. Jelas bahwa χ(G) ≤ |V (G)|, sedangkan cara mudah untuk mencari batas bawah adalah dengan mencari graf bagian komplit terbesar di G. Batas atas dari bilangan kromatik dari graf G, χ(G), sudah banyak diketahui orang, seperti pada Diestel (2005).
Teorema 2.1. Jika G adalah graf sederhana dengan derajat titik maksimum ∆(G), maka χ(G) ≤ ∆(G) + 1
Batas tersebut diperbaiki oleh Brook sebagai berikut:
Teorema 2.2. Misalkan G adalah graf sederhana, terhubung, dan dengan derajat titik maksimum ∆(G). Jika G bukan graph komplit dan bukan siklus ganjil, maka χ(G) ≤ ∆(G).
-
2.2.2. Greedy Algorithm
Ada beberapa teknik dalam k-pewarnaan graf G berbasis heuristik, salah satunya adalah greedy algorithm yang pernah dikritisi nilai probabilitasnya oleh Kucera (1991).
Teorema 2.3. Apabila d adalah derajat terbesar dari titik di graf G maka G paling tidak mempunyai warna sebanyak d + 1, dengan kata lain bilangan kromatik dari graf G paling banyak d + 1
χ(G) ≤ d + 1
Dalam konteks pewarnaan graf, greedy algorithm berarti memberikan warna untuk beberapa cacah dera jat titik berturutan dimulai dari derajat terbesar untuk memperoleh cacah pewarnaan paling minimum (A.E.Eiben, 1998).
Algoritma yang digunakan dalam penelitian ini adalah algoritma Welsh-Powell yang merupakan bagian dari greedy coloring.Tujuan penggunaan algoritma ini adalah mencari solusi bilangan kromatik suatu graf.Algoritma ini tergolong dalam jenis algoritma Largest Degree Ordering (LDO) yaitu algoritma yang memprioritaskan pewarnaan simpul berdasarkan urutan dari dera jat tertinggi.Menurut Welsh dan Powell (1967),
Langkah-langkah penyelesaian pewarnaan titik menggunakan algoritma Welsh-Powell memiliki empat tahapan yaitu (1) urutkan simpul-simpul dari graf G dalam derajat yang menurun dari yang terbesar (urutan seperti ini dimungkinkan tidak unik karena beberapa simpul bisa b erdera jat sama); (2) gunakan satu warna untuk mewarnai simpul pertama (simpul dengan dera jat tertinggi) dan simpul-simpul lain (dalam urutan yang berurut) yang tidak adjacent dengan simpul pertama tersebut; (3) mulai lagi dengan simpul derajat tertinggi berikutnya di dalam daftar terurut yang belum diwarnai dan ulangi proses pewarnaan simpul dengan menggunakan warna kedua; (4) ulangi penambahan warna-warna sampai semua simpul telah diwarnai.
-
2.3. Interferensi dan Medan Listrik
Gelombang elektromagnetik sebagai suatu gelombang yang dapat merambat tanpa medium terjadi akibat interaksi antara medan magnet dan medan listrik. Gelombang radio merupakan bagian dari gelombang elektromagnetik pada spektrum frekuensi radio dengan panjang gelombang lebih dari 10-3 meter dan berada pada daerah MHz (gambar 3).
AM FM and VHF UHF
r—^—i—i—Iiiii
O IOO 300 500 700 900
Frequei
(MHz
Gambar 3. Frekuensi Radio dalam MHz
Interferensi antara dua gelombang atau lebih disebabkan salah satunya oleh kuat medan listrik pada suatu titik. Menurut J.H. Kraus (1994), interferensi terjadi jika kuat medan listrik E > 2, 5 N/C. Kuat medan listrik dipengaruhi oleh beberapa faktor yaitu daya pancar antena(Wt/Watt), konstanta direktivitas(D), dan jarak antara dua titik (d/meter)yang dirumuskan sebagai berikut:
30 · Wt · D
E=
d
(1)
Untuk menghitung jarak antara dua titik pada rumus (1), John Meeus (1991) menggunakan formula (4.2)terlebih dahulu untuk menghitung sudut antara kedua titik (s) dengan mempertimbangkan titik koordinat Bujur dan Lintang dari dua titik tersebut.
arc cos(s) = sin(L1) · sin(L2) + cos(L1) · cos(L2) · cos(B1 - B2) (2)
Selanjutnya jika sudut sdalam derajat, maka jarak kedua titik adalah d kilometer dengan memperhitungkan jarak antara pusat bumi-ekuator (6.378,137 km) dan π =
3, 14, yaitu
6378,137·π·s d=
180
(3)
-
3. Hasil dan Pembahasan
Ketimpangan antara persediaan spektrum frekuensi radio gelombang dan peningkatan jumlah stasiun radio menjadi salah satu permasalahan yang muncul di Daerah Istimewa Yogyakarta. Untuk itu diperlukan mana jemen radio frequency unitdalam rangka menghindari terjadinya interferensi gelombang transmisi antara dua atau lebih stasiun radio.Persoalan ini dapat dika ji pengaturannya menggunakan prinsip vertex coloring. Untuk lebih jelasnya berikut adalah langkah-langkah aplikasi vertex coloring pada radio frequency unit:
-
1. Menganalisis interferensi gelombang transmisi dengan mengkalkulasi jarak antara sebarang dua titik koordinat (stasiun radio) dan kuat medan listrik antara sebarang dua titik.
-
2. Mentransformasi stasiun radio beserta garisnya ke bentuk graf. Seperti yang telah dijelaskan pada landasan teori, graf terdiri atas simpul dan garis. Simpul merepresentasikan semua lokasi stasiun radio dan garis merepresentasikan dua sebarang stasiun radio yang saling terinterferensi yaitu jika E > 3, 5 N/C yang selanjutnya simpul-simpul tersebut saling dihubungkan.
-
3. Mewarnai setiap simpul pada graf dengan menggunakan algoritma Welsh-Powell. Selain untuk mengetahui stasiun radio mana saja yang diperbolehkan dalam satu kanal, diperoleh juga jumlah bilangan kromatik yang akanberguna pada tahap berikutnya.
-
4. Menentukan alternatif penyelesaian manajemen radio frequency unit dengan menyajikan dalam graf berwarna.
Berikut disajikan radio frequency unit di Daerah Istimewa Yogyakarta dengan mengambil data sampel 10 stasiun radio secara acak yang diperoleh dari LPJ Balai Monitor Spektrum Frekuensi Radio Kelas II DIY 2011 (Tabel 4).
Tabel 4.Sumber data LPJ Balai Monitor Spektrum Frekuensi Radio Kelas II DIY 2011
|
No |
Nama Radio |
Jenis Antena |
Daya Pancar Antena (Watt) |
Konstanta Direktivitas |
Koordinat Pemancar |
Garis lintang/ bujur |
|
1 |
Q-Radio |
Cycloid |
2500 |
0.4 |
7◦ 44'47.4'' S/ 110◦23'36.5" E |
7.7465/ 110.3935 |
|
2 |
I-Radio |
MS-1 |
2500 |
0.7 |
7o47'58.9'' S/ 110o 19’49.1 ” E |
7.9969/ 110.3303 |
|
3 |
Bantul Radio |
Circulair |
2000 |
0.9 |
7°46'58.3" S/ 110◦ 20'53" E |
7.7828/ 110.3481 |
|
4 |
JIZ FM |
MS-1 |
2500 |
0.4 |
7◦45'42.6" S/ 110◦24,29.3" E |
7.7618/ 110.4081 |
|
5 |
Sasando FM |
MS-1 |
2000 |
0.7 |
7°47‘ 1.0" S/ 110o23’50.0" E |
7.7836/ 110.3972 |
|
6 |
UTY FM Medari |
OMB |
3000 |
0.7 |
7o40'43.1'' S/ 110o20, 18.0" E |
7.6786/ 110.338 |
|
7 |
RRI Pro-1 |
Circular |
15000 |
0.9 |
7°46' 16.3" S/ 110o24’29.3” E |
7.7712/ 110.408 |
|
8 |
MQ FM |
Circular |
1500 |
0.9 |
7◦44'54" S/ 110◦24'38.5" E |
7.7348/ 110.4107 |
|
9 |
MBS |
Sige |
2500 |
0.6 |
7o49'34'' S/ 110o23'29'' E |
7.8261/ 110.3914 |
|
10 |
Argososro FM |
Folded Cycloid |
700 |
0.7 |
7o47'43.6'' S/ 110o23'6.9'' E |
7.7954/ 110.3852 |
Langkah-langkah penyelesaian alternatif manajemen radio frequency unit di Daerah Istimewa Yogyakarta adalah sebagai berikut:
-
1. Analisis interferensi gelombang transmisi menggunakan kaidah kuat medan listrik. Pada tahap ini data pada tabel 4 diperlukan untuk mengetahui kuat medan listrik antara satu radio dengan lainnya. Jarak antara dua stasiun radio dapat dihitung menggunakan formula (2) dan (3) sedemikian sehingga diperoleh tabel 5 dalam satuan meter. Setelah diketahui jarak tersebut kemudian dapat dilakukan perhitungan kuat medan listrik menggunakan formula (1). Sehingga berdasarkan studi kasus 10 stasiun radio di wilayah Daerah Istimewa Yogyakarta, diperoleh data mengenai kuat medan listrik antara dua sebarang stasiun radio (lihat tabel 6).
Q-Radio
I-Radio
Bantul
Jiz
Sasando
Radio Q
0.00
27846.57
4062.88
1709.96
4128.01
I-Radio
27846.5
0.00
23820.58
26138.9
23720.63
Bantul
4062.88
23820.58
0.00
2398.13
396.44
Jiz
1709.96
26138.99
2398.13
0.00
2427.50
Sasando
4128.01
23720.63
396.44
2427.50
0.00
UTY
7601.88
35414.77
11594.29
9309.75
11705.42
Pro-1
2752.40
25094.40
1388.14
1045.87
1382.70
MQ
1319.60
29138.55
5378.90
3004.25
5431.37
MBS
8856.55
18998.88
4822.46
7154.83
4728.77
Argo-sosro
5441.26
22412.52
1426.99
3743.12
1315.70
|
UTY |
Pro-1 |
MQ |
MBS |
Argo-sosro | |
|
Radio Q |
7601.88 |
2752.40 |
1319.60 |
8856.55 |
5441.26 |
|
I-Radio |
35414.7 |
25094.4 |
29138.5 |
18998.8 |
22412.5 |
|
Bantul |
11594.2 |
1388.14 |
5378.90 |
4822.46 |
1426.99 |
|
Jiz |
9309.75 |
1045.87 |
3004.25 |
7154.83 |
3743.12 |
|
Sasando |
11705.4 |
1382.70 |
5431.37 |
4728.77 |
1315.70 |
|
UTY |
0.00 |
10345.3 |
6360.61 |
16416.5 |
13006.3 |
|
Pro-1 |
10345.3 |
0.00 |
4050.08 |
6108.99 |
2698.35 |
|
MQ |
6360.61 |
4050.08 |
0.00 |
10159.0 |
6746.70 |
|
MBS |
16416.5 |
6108.99 |
10159.0 |
0.00 |
3415.89 |
|
Argo-sosro |
13006.3 |
2698.35 |
6746.70 |
3415.89 |
0.00 |
Tabel 5. Jarak Antara Dua Stasiun Radio (dalam satuan meter)
|
Q-Radio |
I-Radio |
Bantul |
Jiz |
Sasando | |
|
Radio Q |
0 |
1.37307 |
3.64569 |
4.18859 |
3.18973 |
|
I-Radio |
1.37307 |
0 |
1.50564 |
1.07131 |
1.33064 |
|
Bantul |
3.64569 |
1.50564 |
0 |
3.53691 |
10.2929 |
|
Jiz |
4.18859 |
1.07131 |
3.53691 |
0 |
4.15954 |
|
Sasando |
3.18973 |
1.33064 |
10.2929 |
4.15954 |
0 |
|
UTY |
2.87879 |
1.33376 |
2.33103 |
2.60136 |
2.31994 |
|
Pro-1 |
12.1303 |
4.01734 |
17.0809 |
19.6783 |
17.1145 |
|
MQ |
5.53996 |
1.17895 |
2.74398 |
3.67163 |
2.73069 |
|
MBS |
2.2541 |
1.53901 |
3.05472 |
2.50788 |
3.08484 |
|
Argososro |
1.64365 |
0.80987 |
3.20958 |
1.98172 |
3.34257 |
|
UTY |
Pro-1 |
MQ |
MBS |
Argososro | |
|
Radio Q |
12.1303 |
5.53996 |
2.2541 |
1.643649 | |
|
I-Radio |
1.33376 |
4.01734 |
1.17895 |
1.53901 |
0.8098663 |
|
Bantul |
2.33103 |
17.0809 |
2.74398 |
3.05472 |
3.2095762 |
|
Jiz |
2.60136 |
19.6783 |
3.67163 |
2.50788 |
1.9817188 |
|
Sasando |
2.31994 |
17.1145 |
2.73069 |
3.08484 |
3.3425725 |
|
UTY |
0 |
6.25683 |
2.52335 |
1.65564 |
1.0631154 |
|
Pro-1 |
6.25683 |
0 |
3.16224 |
2.71407 |
2.3340486 |
|
MQ |
2.52335 |
3.16224 |
0 |
2.10465 |
1.4760907 |
|
MBS |
1.65564 |
2.71407 |
2.10465 |
0 |
2.0744681 |
|
Argososro |
1.06312 |
2.33405 |
1.47609 |
2.07447 |
0 |
Tabel 6. Kuat Medan Listrik Dua Sebarang Radio (dalam satuan N/C atau V/M)
-
2. Transformasi stasiun radio beserta garis yang terhubung ke dalam graf. Stasiun radio dalam hal ini disebut sebagai titik dalam graf, sedangkan garis dipengaruhi oleh tingkat interferensi antara pasangan stasiun radio. Data pada tabel 6 menunjukkan kuat medan listrik antara satu radio dengan lainnya yang dikatakan saling terinterferensi jika nilainya > 3, 5 N/C (J.H. Kraus: 1994). Dengan kata lain untuk setiap kuat medan listrik < 3, 5 N/C (diarsir), maka tidak ada garis yang menghubungkan antara pasangan stasiun radio, sebagai contoh stasiun UTY dan I-Radio memiliki nilai E = 1.33 N/C. Sehingga berdasarkan data pada tabel 6 dapat dibuat representasi grafnya (lihat gambar 4).
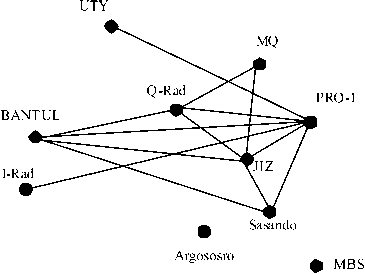
Gambar 4. Representasi Graf Berbasis Interferensi Gelombang
-
3. Pewarnaan simpul menggunakan algoritma Welsh-Powell
Berdasarkan data pada gambar 4, selanjutnya dapat dilakukan pewarnaan simpul merujuk pada algoritma Welsh-Powell. (1) Diawali dengan mengurutkan simpul-simpul dari graf G dalam dera jat menurun dari yang terbesar, dalam hal ini berturut-turut Pro-1, Jiz, Bantul, Q-Radio, Sasando, MQ, I-Radio, UTY, Ar-gososro, dan MBS; (2) menentukan satu warna yaitu merah(disimbolkan dengan angka 1) untuk mewarnai simpul pertama yaitu Pro-1 dan simpul-simpul lain yang tidak adjacent dengan simpul Pro-1 yaitu MQ, MBS, dan Argososro; (3) dilanjutkanpewarnaan simpul biru (disimbolkan dengan angka 2)untuk derajat tertinggi berikutnya yaitu Jiz dan simpul-simpul lain yang tidak adjacent dengan simpul Jiz yaitu UTY dan I-Radio; (4) ulangi langkah tersebut hingga diperoleh pewarnaan hijau (disimbolkan dengan angka 3)dan kuning (disimbolkan dengan angka 4)yang berarti semua simpul telah diwarnai (lihat gambar 5).

Gambar 5. Hasil Pewarnaan Graf Berbasis Algoritma Welsh-Powell
-
4. Penentuan alternatif solusi radio frequency unit yang tersaji dalam graf berwarna. Gambar 5 menunjukkan bahwa bilangan kromatik k = 4, sehingga 10 stasiun radio tersebut dapat dibagi ke dalam empat klaster yaitu:
-
(a) Merah : 57, 99, 75, 119
-
(b) Biru : 12, 4, 67
-
(c) Hijau : 111, 162
-
(d) Kuning : 170
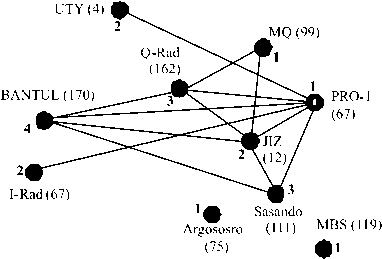
Gambar 6. Distribusi Frekuensi Radio
Dengan demikian diperoleh alternatif pembagian frekuensi stasiun radio sebagaimana diilustrasikan pada gambar 6.
-
4. Kesimpulan
Setelah melakukan pengkajian mengenai manajemen radio frequency unit, dapat disimpulkan bahwa graph coloring menggunakan pendekatan greedy algorithm khususnya upper bound bilangan kromatik dapat diaplikasikan dalam memberikan alternatif solusi terhadap permasalahan manajemen radio frequency unit khususnya berkaitan dengan optimalisasi jumlah klaster. Hal ini dilakukan dengan cara memodelkan beberapa stasiun radio ke dalam perspektif graf dengan mempertimbangkan tingkat interferensi yaitu kuat medan listrik kemudian dianalisis menggunakan kaidah upper bound bilangan kro-matik untuk memperoleh jumlah minimum klaster frekuensi radio.
Daftar Pustaka
-
[1] Liang, C.,Zheng, G., Zhu, N., Zhe, T., Lu, S., dan Chen, L.: A New Environmental Heat Stress Index for Indoor Hot and Humid Envirenments Based on Cox Regression. Journal International of Buliding and Environment, 46, 2472-2479 (2011)
-
[2] Balakrishnan V.K., 1997,Scaum’s Outlines Graph Theory, McGraw-Hill.
-
[3] Bollobas Bela, 1998,Modern Grapf Theory, Springer.
-
[4] Bondy, J.A dan Murty, U.S.R., 1976,Graph Theory With Applications, New York: MacMillan Press.
-
[5] DiestelReinhard, 2005, Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag.
-
[6] D.J.A. Welsh & M.B. Powell, 1967, An upper bound for the chromatic number of a graph and its application to timetabling problems, The Computer Journal, vol.10, pp. 85-86.
-
[7] A.E. Eiben, dkk., 1998, Graph Coloring with Adaptive genetic Algorithm, Cite-Seerx Digital Library.
-
[8] Gross, Jonathan L. dan Yellen Jay, 2003, Handbook of Graph Theory, CRC Press.
-
[9] Hamdy A. Taha, 2007, Operations Research: an Introduction, Prentice Hall, NJ.
-
[10] Hirose, Akira. 1984, Introduction to Wave Phenomena. Canada: John Wiley & Sons Publisher
-
[11] J.A, Boundy, U.S.R, Murty. 1976. Graph Theory with Application. New York : North-Holan
-
[12] Jean Meeus: Astronomical Algorithm, Willmann-Bell, Virginia, 1991
-
[13] Jensen, T.R. dan Toft, B., 1995, Graph Coloring Problems, Wiley-Interscience, NewYork.
-
[14] Krauss, John D. 1994. Antennas. U.S.A: Mc-Graw-Hill Series
-
[15] L. Kucera, 1991, The greedy coloring is a bad probabilistic algorithm, Journal of Algorithms, 12:674-684.
-
[16] Lipschutz, S, Lipson, M. 2007. Matematika Diskrit, Schaum’s Outlines. New York: Mc Graw-Hill
-
[17] Nadzir, Muhammad. 1998. Metode Penelitian . Jakarta: Ghalia Indonesia Regulasi Penyiaran. http://www.postel.go.id, diakses pada tanggal 9 November 2012 pukul 19:12 WIB
-
[18] Pozar,D.M.MicrowaveEngineering.JohnWiley & Sons,2ndedNewYork, 1998
-
[19] Siahaan, Margaretha. 2010. Studi Pewarnaan Graf pada Radio Frequency Assignment Problem. http://std.stei//struktur-diskrit.pdf diakses pada tanggal 26 Oktober 2011 pukul 06:38 WIB
-
[20] Siamak Firouzian, dkk, 2011, Coloring Fuzzy Graphs and Traffic Light Problem, The Journal of Mathematics and Computer Science Vol .2: 431-435.
-
[21] Siang, Jong Jek. 2002. Matematika Diskrit dan Aplikasinya pada Ilmu Kom-puter.Yogyakarta : Andi
-
[22] Suparyanto, Tri. 2012. Directory Radio Televisi Daerah Istimewa Yo-gyakarta,Yogyakarta: Komisi Penyiaran Daerah (KPID) D.I Yogyakara
-
[23] Supiyanto. 2006. Fisika 1 Untuk SMA/MA Kelas X. Jakarta: Phibeta
-
[24] Walter Klotz, 2002, Graph Coloring Algorithms, Mathematik-Bericht 5, 1-9, TU Clausthal. Germany.
-
[25] Wangsness, Roald K. 1986. Electromagnetic Fields.Singapore : John Wiley and Sons
-
[26] Wilson, Robert A. 2002. Graph, Colouring and The four Colour Theorem. New York: Oxford University Press
-
[27] Winston, Wayne L., 2000, Operation Research: Applications and Algorithms, Edisi keempat, Canada: Thomson.
-
[28] ————————-. 2003 Peraturan Radio, Jakarta : Himpunan Komunikasi Inter-
nasional
Discussion and feedback