Penentuan Rute Terpendek dengan Menggunakan Algoritma Dijkstra pada Jalur Bus Sekolah
on
Jurnal Matematika Vol. 10, No.2, Desember 2020, pp. 116-123
Article DOI: 10.24843/JMAT.2020.v10.i02.p128
ISSN: 1693-1394
Penentuan Rute Terpendek dengan Menggunakan Algoritma Dijkstra pada Jalur Bus Sekolah
I Putu Winada Gautama
Universitas Udayana e-mail: winadagautama@unud.ac.id
Koko Hermanto
Universitas Teknologi Sumbawa e-mail: kokohermato@gmail.com
Abstract: The role of public transport or school buses is very important in reducing traffic violations for underage drivers. School bus transportation is becoming popular in Bali. Especially in Denpasar City, Denpasar City transportation service has been operating in September 2017. One of the optimizations that can be done is to determine the shortest distance from the school bus line. The shorter the distance traveled, of course, has an impact on cost and time. Costs incurred can be minimized and travel time is more efficient. Based on the results obtained, the fuel costs incurred for the morning shift school bus were IDR 70,132. These results can provide an overview for the Denpasar City Transportation Agency regarding the application of mathematics in determining routes that can optimize fuel costs.
Keywords: CVGRP, Optimization, Transportation
Abstrak: Peran angkutan umum atau bus sekolah sangat penting dalam mengurangi pelanggaran lalu lintas bagi pengemudi di bawah umur. Transportasi bus sekolah menjadi populer di Bali. Khusus di Kota Denpasar, layanan transportasi Kota Denpasar baru beroperasi pada September 2017. Salah satu optimalisasi yang bisa dilakukan adalah dengan menentukan jarak terpendek dari jalur bus sekolah. Semakin pendek jarak yang ditempuh tentunya berdampak pada biaya dan waktu. Biaya yang dikeluarkan dapat diminimalisir dan waktu tempuh lebih efisien. Berdasarkan hasil yang diperoleh, biaya bahan bakar yang dikeluarkan untuk bus sekolah shift pagi sebesar Rp70.132. Hasil tersebut dapat memberikan gambaran bagi Dinas Perhubungan Kota Denpasar mengenai penerapan matematika dalam menentukan rute yang dapat mengoptimalkan biaya bahan bakar.
Kata Kunci: CVGRP, Optimasi, Transportasi
Salah satu upaya untuk menekan angka kecelakaan lalu lintas di kalangan pelajar adalah mengoptimalkan angkutan umum untuk angkutan siswa. Angkutan umum atau bus sekolah dapat meringankan biaya sekolah dalam hal transportasi sehingga orang tua siswa tidak akan terbebani. Disamping itu, orang tua siswa juga tidak akan khawatir karena menggunakan angkutan sekolah siswa memiliki kepastian jadwal pemberangkatan ke sekolah / pulang sekolah karena pada bus sekolah dilengkapi jadwal pemberangkatan dan waktu pemberhentian sesuai dengan lokasinya. Dikutip dari www.bali.antaranews.com tercatat pada bulan Juli 2018 sebanyak 1084 orang yang melanggar lalu lintas. Sebanyak 757 orang atau sekitar 70% pengendara di bawah umur. Hal ini tentunya sangat membahayakan bagi pengendara dibawah umur yang tergolong pelajar sebab pelanggaran lalu lintas adalah salah satu penyebab terjadinya kecelakaan lalu lintas. Peran angkutan umum atau bus sekolah sangat vital dalam mengurangi pelanggaran lalu lintas bagi pengendara di bawah umur. Alat transportasi bus sekolah mulai populer di Bali. Khususnya di kota Denpasar, dinas perhubungan Kota Denpasar sudah beroperasi pada bulan September 2017. Bus sekolah yang beroperasi di Kota Denpasar memiliki fasilitas aplikasi mobile yang bernama “Si_Bused” (Sistem Informasi Bus Sekolah). Fitur dari aplikasi tersebut diantaranya memberikan notifikasi, live CCTV di dalam kendaraan, mengkomunikasikan perubahan jadwal sekolah secara realtime, merekam data identitas penumpang secara akurat, memberikan data petugas yang bertugas waktu itu, dan memberikan berbagai informasi penting lainnya. Bus Sekolah tersebut dilengkapi wifi gratis, full AC, multimedia, smart card, slot charger serta asuransi penumpangSalah satu optimasi yang dapat dilakukan adalah menentukan jarak terpendek dari rute bus sekolah. Semakin pendek jarak yang dilalui tentunya berdampak pada biaya dan waktu. Biaya yang dikeluarkan dapat diminimalkan dan waktu tempuh lebih efisien.
Beberapa penelitian sebelumnya, (Hermawan et al 2017), mengenai sistem optimasi rute kuliner di Malang, yang menggunakan optimasi Travelling Salesman Problem (TSP) Dengan Algoritme Bee Colony (lebah). Dengan merepresentasikan titik jarak dengan pasukan lebah, dilakukan perhitungan dengan fase employee bee, scout bee dan onloker bee. Penelitian serupa juga pernah dilakukan oleh (Karimah et al 2017), dengan judul optimasi multiple travelling salesman problem (M-TSP) pada pendistribusian air minum menggunakan Algoritme Genetika. Dengan adanya berbagai metode pendekatan untuk menyelesaikan masalah optimasi, peneliti menggunakan algoritma dijkstra untuk mengoptimalkan masalah travelling salesman problem pada bus sekolah di Kota Denpasar.
Dalam penelitian ini menggunakan Algoritma Djikstra dalam membuat model CVGRP. Tujuan CGVRP adalah untuk menentukan koleksi biaya minimum dari m tur kendaraan yang berawal dan berakhir di gudang sehingga vertek dari tiap graph dikunjungi tepat satu kali dengan melakukan jalur Halmiton pada tiap vertek, serta muatan masing-masing kendaraan tidak melebihi kapasitas. Setiap rute kendaraan mengunjungi tepat satu vertek dari sejumlah kelompok dan memenuhi kendala kapasitas.
Algoritma Dijkstra merupakan sebuah algoritma digunakan untuk menentukan rute terpendek pada graph berarah atau graph tak berarah yang memiliki bobot tanpa mengenumerasi secara eksplinsit semua rute alternatif yang mungkin menjadi solusi rute optimal. Prinsip algoritma Dijkstra dalam menentukan rute terpendek dari suatu masalah jaringan yang dimodelkan dalam graph adalah pada waktu penentuan rute alternatif yang kemungkinan menjadi solusi, setiap bobot dari vertek yang belum dipilih akan dianalisis, lalu dipilih vertek dengan bobot yang paling kecil. Apabila ada bobot yang lebih kecil melalui vertek tertentu, maka rute akan berubah mengikuti bobot yang lebih kecil tersebut, artinya rute lintasan akan berubah. Algoritma Dijkstra akan berhenti ketika semua vertek sudah terlewati. Jadi, metode GVRP, CGVRP, dan algoritma Djikstra untuk menentukan rute terpendek penjemputan siswa adalah metode yang digunakan dalam penelitian ini.
Proses pengumpulan data sebelumnya sudah mendapatkan ijin dari kepala Unit Pelayanan Teknis Transportasi Darat Dinas Perhubungan Kota Denpasar. Pengumpulan data dengan melakukan wawancara langsung dengan salah satu petugas UPT Pelayanan Transportasi Darat dan melakukan survei ke lokasi titik penjemputan dan penurunan siswa. Adapun data yang diperoleh yaitu jumlah bus sekolah, rute bus sekolah, dan lokasi dropzone. Terdapat delapan buah bus, diantaranya 2 bus berukuran besar dan 6 bus berukuran kecil yang dapat menampung kurang lebih 25 siswa. Bus sekolah ini lebih mengutamakan pada keamanan dan kenyamanan siswa sekolah. Bus sekolah tersebut juga dilengkapi dengan fasilitas Smart Card, AC, CCTV, WiFi, Multimedia, GPS, dan Aplikasi Android SiBused. Aplikasi Sibused memungkinkan orang tua siswa untuk mengetahui lokasi bus sekolah. Bus sekolah tersebut beroperasi dengan trayek-trayek yang berbeda.
Untuk menjadi penumpang Bus sekolah kota Denpasar, calon penumpang mendaftarkan diri ke UPT Transportasi Darat melalui telepon atau datang langsung ke
kantor. Tata cara pendaftarannya antara lain; mengisi formulir pendaftaran dan surat kesanggupan, melaporkan ke pihak sekolah, dan melengkapi surat-surat lainnya dari UPT Transdar. Hasil pendataan siswa akan menjadi acuan untuk melakukan penjemputan dan pengantaran siswa dari dan ke lokasi dropzone yang terdekat dengan tempat tinggal siswa serta sekolah tempat siswa bersekolah. Daerah pelayanan Bus Sekolah ini untuk seluruh kecamatan yang ada di Denpasar.
Penjemputan dan pengantaran siswa dilakukan menjadi empat shift. Shift pagi putaran pertama pukul 05:40 WITA-07:00 WITA, Shift pagi putaran kedua pukul 10:57 WITA-11:40 WITA, Shift siang putaran pertama pukul 12:40 WITA-15:00 WITA, dan terakhir shift siang putaran kedua pukul 17:30 WITA-18:30 WITA.
Jarak setiap dropzone ditentukan dengan bantuan google maps yang dilakukan pada waktu bersamaan. Selanjutnya setiap dropzone dikelompokan berdasarkan keluarahan di Kota Denpasar dengan memperhatikan kapasitas bus sekolah, jika melebihi kapasitas maka dibentuk kelompok baru. Berikut ini disajikan tabel pengelompokan dropzone
Tabel 1. Pengelompokan Dropzone Berdasarkan Kelurahan
|
Bus |
Kecamatan |
Kelurahan |
Area Penjemputan Siswa |
Jumlah Siswa |
|
V1 |
Denpasar Barat |
Dauh Puri |
Dropzone Jl Patimura (22) |
2 |
|
Denpasar Barat |
Pemecutan |
Dropzone Bung Tomo (17) |
2 | |
|
Denpasar Selatan |
Pedungan |
Depan Toko Wikowi (96) |
3 | |
|
Denpasar Timur |
Dangin Puri |
Banjar Tampak Gangsul (103) |
1 | |
|
Halte Nangka Selatan (40) |
9 | |||
|
Hotel Nuansa Indah (104) |
1 | |||
|
Denpasar Timur |
Kesiman |
Halte Sarbagita Kesiman (41) |
2 | |
|
Plang SD Saraswati 5 (71) |
4 | |||
|
V2 |
Dropzone TL Surabi (74) |
4 | ||
|
Denpasar Timur |
Penatih |
Wantilan Penatih Trenggana (85) |
4 | |
|
Indomaret Trenggana (48) |
2 | |||
|
Dropzone Jl. Nagasari (21) |
4 | |||
|
LPD Bekul (53) |
9 | |||
|
V3 |
Toko Buku Asiki Siulan (75) |
3 | ||
|
Dapurku Siulan (13) |
4 | |||
|
Toko Bangunan UD Sri Re-jeki (94) |
1 | |||
|
Br Palagiri (95) |
1 | |||
|
ASIKI Trenggana (4) |
2 | |||
|
Pertigaan Nagasari (60) |
6 |
|
Kantor Lurah Penatih (50) |
4 | |||
|
Denpasar TImur |
Sumerta |
DropzoneJL. Subita (29) |
1 | |
|
V4 |
Denpasar Utara |
Peguyangan |
Halte Ayani (39) |
4 |
|
Indomaret Ayani (47) |
4 | |||
|
Alfamart Ayani (1) |
1 | |||
|
Cening Laundry (66) |
6 | |||
|
Dropzone Simpang lembu Sora (26) |
1 | |||
|
TB Tiga Pilar Mas (73) |
4 | |||
|
Dropzone Dr. Umum Jl Per-tulaka (16) |
2 | |||
|
Halte Antasura (38) |
3 | |||
|
V5 |
Pertigaan Suradipa 2 (61) |
8 | ||
|
Toko Ratu (79) |
7 | |||
|
Daimaru (92) |
1 | |||
|
Indomaret Antasura (44) |
4 | |||
|
Gang Sutra Jl Antasura (97) |
2 | |||
|
TL Antasura wr Mina (87) |
8 | |||
|
TL Pasar Peguyangan (98) |
1 | |||
|
Depan Toko New Bintang pangan (100) |
1 | |||
|
V6 |
Toko Agung Jl Peguyangan (101) |
1 | ||
|
Denpasar Utara |
Tonja |
Perumahan Padma Indah (102) |
4 | |
|
Denpasar Utara |
Ubung |
Dunkin Donut Cokroaminoto (30) |
4 | |
|
Depan Terminal Ubung (15) |
7 | |||
|
Indihome Ubung (43) |
2 | |||
|
Toko Chacha (76) |
8 | |||
|
V7 |
Kurnia Motor Cargo (52) |
2 | ||
|
Pasar Pidada (57) |
2 | |||
|
Hotel Ferry Antho Pidada (32) |
2 | |||
|
Indomaret Green Kori (46) |
5 | |||
|
Total |
163 |
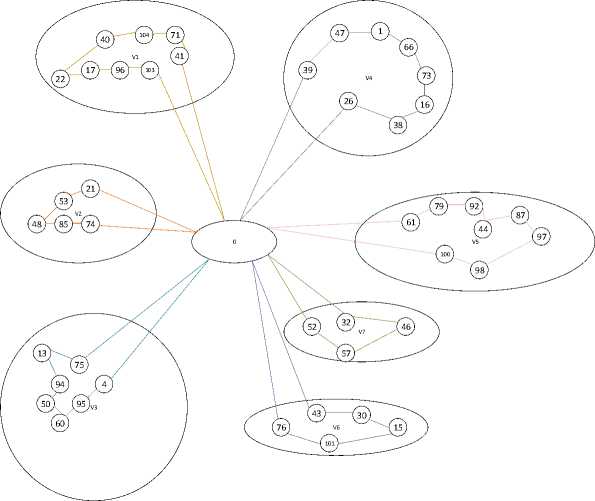
Berikut ini adalah ilustrasi yang diperoleh berdasarkan Tabel 1.


Gambar 1. Pengelompokan Dropzone
Selanjutnya akan diukut jarak minimal antar dropzone, dengan menggunakan metode Djikstra disusunlah model GVRP. Vertek pada masing kelompok diukur dengan menentukan jarak minimal dengan MAKO kemudian dihubungkan dengan edge. Jika bus sekolah mengunjungi lebih dari satu kelompok, maka akan dipilih dua dropzone dari kelompok yang berbeda. Selanjutnya diperoleh model GVRP yang tertuang dalam Gambar 2.

Gambar 2. Model GVRP Dropzone
Selanjutnya dibentuk model CGVRP dengan menggunakan metode Djikstra, dengan menentukan rute terpendek dropzone pada masing-masing kelompok.
Gambar 3. Model CGVRP Dropzone
Berdasarkan Gambar 3, total rute Bus Sekolah Denpasar untuk shift pagi sepanjang 95,5 km. Bus Sekolah tersebut menggunakan bahan bakar pertadex, dimana 1 liter dengan harga Rp 9.400 dapat menempuh 12,8 km. Jadi total biaya bahan bakar bus sekolah tersebut adalah Rp 70.132,-.
Berdasarkan hasil yang diperoleh bahwa biaya bahan bakar yang dihabiskan bus sekolah shift pagi adalah Rp 70.132,-. Hasil ini dapat memberikan gambaran untuk Dinas Perhubungan kota Denpasar mengenai terapan matematika dalam menentukan rute yang dapat mengoptimalkan pengeluaran biaya bahan bakar.
Ucapan Terima Kasih
Penulis mengucapkan terima kasih kepada LPPM Universitas Udayana yang telah memberi dukungan finansial terhadap penelitian ini.
Daftar Pustaka
Acharjya, D.P. dan Sreekumar. 2009. Fundamental Approach to DiscreteMathematics, Second Edition. New Delhi: New Age Internasional (P)Limited.
Arefin, Rajib. Dkk. 2013. Additive Algorithm for Solving 0-1 Integer Linear Fractional-Programming Problem. Department of Mathematics, Dhaka Uni-versty.DhakaUniv. J. Sci. 61(2): 173-178, 2013 (July)
Gendreau, Michel. Dkk. 2010. A Tabu Search Heuristic for the Vehicle Routing Problem. Jstor. Management Science, Vol. 40, No. 10 (Oct., 1994), pp. 1276-1290.
Hermawan, Arif, Hidayat, I., & Budi. 2017.Sistem Optimasi Rute Tempat
WisataKuliner Di Malang MenggunakanAlgoritma Bee Colony.S1. Universitas Brawijaya.
Karimah, Sayyidah. Cholissodin, I., & Indriati.2017. optimasi multiple travelin salesman problem (M-TSP) pada pendistribusian air minum menggunakan algoritme genetika S1. Universitas Brawijaya.
Munawir, Hafidh, dan Narima, Agus. 2012. Penentuan Rute Pendistribusian KertasKarton Model Studi Kasus: PT. Papertech Indonesia Unit II Mage-lang.Simposium Nasional RAPI XI FT UMS. ISSN:1412-9612.
Mutakhiro, Iing. 2007. Pemanfaatan Metode Heuristik Dalam Pencarian JalurTerpen-dek Dengan Algoritma Semut Dan Algoritmna Genetik. Yogyakarta: Universitas Islam Indonesia.
P. C. Pop. 2007. New Integer Programming Formulations of the GeneralizedTravelling Salesman Problem. American Journal of Applied Sciences 4 (11):932-937, 2007, ISSN 1546-9239
Santosa, Budi. 2008. Matlab Untuk Statistika dan Teknik Optimasi Aplikasi untuk Rekayasa dan Bisnis. Yokyakarta: Graha Ilmu.
Scheinerman, Edward R. 2006. Mathematics A Discrete Introduction. Boston, Amerika Serikat: Department of Applied Mathematics and Statistcs The John Hopkins University.
Susanna S. 2012. Discrete Mathematics with Application, 4thEdition. Boston, Amerika Serikat: DePaul University.
123
Discussion and feedback