Estimasi Maksimum Likelihood Melalui Algoritma Ekspektasi Maksimasi Untuk Model Regresi Linear dengan Data Hilang

Jurnal Matematika Vol. 10, No.2, Desember 2020, pp. 105-115

Article DOI: 10.24843/JMAT.2020.v10.i02.p127

ISSN: 1693-1394

Estimasi Maksimum Likelihood

Melalui Algoritma Ekspektasi Maksimasi Untuk Model Regresi Linear dengan Data Hilang

Harizahayu

Politeknik Negeri Medan ,Jl. Almamater No. 1 Kampus USU 20155, Medan e-mail: harizahayu@polmed.ac.id

Abstract: Data is one of the important points in any data analysis, because it is impossible for the analysis to be carried out if the data is incomplete. The data used is expected to be good data. But in reality, the data is often not what we expect. Incomplete data makes the process of drawing conclusions more difficult. If missing data is ignored, it will lead to biased or invalid conclusions. In this study, a linear regression model will be used. Regression analysis is a statistical analysis performed to model the relationship between Y (the dependent variable) and X categorical random variable (the independent variable). For Y, the continuous variable and X are discrete variables, assuming Y the fully observable variable and X there are several missing variables. The classification of missing data that will be compared consists of three classifications, namely: MCAR, MAR, and MNAR. This discussion ends with a case study regarding the estimation of the missing data value in the xerostomia data presentation variable using the EM algorithm to calculate the maximum likelihood estimate (MLE) in the linear regression model with three missing data classifications.

Keywords: linear regression, missing data, missing completely at random,

missing at random, missing not at random, Lagrange multipliers, expectation maximization.

Abstrak: Data merupakan salah satu poin penting dalam setiap analisis data, karena tidak akan mungkin analisis dapat dilakukan jika datanya tidak lengkap. Data yang digunakan diharapkan merupakan data yang baik. Namun pada kenyataannya, sering-kali data tidak sesuai dengan yang kita harapkan. Data yang tidak lengkap menyebabkan proses mengambil kesimpulan mejadi lebih sulit. Jika data yang hilang diabaikan, maka akan menyebabkan kesimpulan bias atau tidak valid. Dalam penelitian ini akan digunakan model regresi linear. Analisis regresi adalah analisis statistik yang dilakukan untuk memodelkan hubungan antara ¥ (variabel dependen) dan X variabel random kategorik (variabel independen). Untuk Y variabel kontinu dan X variabel dis-krit, dengan mengasumsikan Y variabel yang seluruhnya teramati dan X terdapat beberapa variabel yang hilang. Adapun klasifikasi data hilang yang akan dibandingkan terdiri dari tiga klasifikasi yaitu: MCAR, MAR, dan MNAR. Pembahasan ini diakhiri dengan studi kasus mengenai estimasi nilai data hilang pada variabel presentasi data xerostomia dengan menggunakan algoritma EM untuk menghitung maksimum likelihood estimasi (MLE) pada model regresi linear dengan tiga klasifikasi data hilang.

Kata kunci: regresi linear, data hilang, MCAR, MAR, MNAR, Lagrange multipliers, ekspektasi maksimisasi

1. Pendahuluan

Analisis regresi merupakan suatu metode dalam statistik yang banyak digunakan pada penelitian dalam berbagai bidang untuk mempelajari hubungan antara variable dependen dan independen (Angelini, 2018). Analisis regresi yang memiliki satu variable independen disebut analisis regresi sederhana. Dalam analisis regresi terdapat sepasang data, yaitu data untuk variable independen dan dependen. Data inilah yang digunakan dalam analisis. Karena data merupakan bahan utama yang nantinya akan diolah sehingga menghasilkan suatu kesimpulan dari apa yang diduga pada awal penelitian. Pengumpulan data pengamatan tidak selalu berjalan dengan mulus, adakalnya terjadi bermacam kendala yang mengakibatkan data menjadi tidak lengkap atau memuat beberapa nilai yang hilang, sehingga menyulitkan pada saat melakukan analisis statistik.

Data yang hilang atau data yang rusak adalah hal biasa dalam kumpulan data dunia nyata, hal ini mempengaruhi estimasi dan pengoperasian model analitik di mana kelengkapan diasumsikan atau diperlukan. Data yang hilang atau data yang rusak adalah hal biasa dalam kumpulan data dunia nyata, hal ini mempengaruhi estimasi dan pengoperasian model analitik di mana kelengkapan diasumsikan atau diperlukan. Efek yang mungkin terjadi dari informasi data hilang sebagian besar didasarkan pada penyebab atau alasan data menjadi hilang atau tidak lengkap. Skenario kasus terbaik adalah penjelasan untuk data yang hilang sepenuhnya acak. Misalnya, untuk subset peserta secara acak, mungkin peneliti studi yang terganggu secara tidak sengaja lupa mengukur tinggi badan (Sainani, 2015).

Analisis retrospektif data klinis dunia nyata menghadapi tantangan penyebab data hilang karena tidak adanya beberapa elemen data. Secara historis, data yang hilang ditangani dengan terlebih dahulu mengklasifikasikan keberadaannya menjadi salah satu dari tiga kategori: missing completely at random (MCAR), missing at random (MAR) dan missing not at random (MNAR). Teknik imputasi terus dikembangkan dan diuji untuk mengukur kapasitasnya dalam memitigasi dampak negatif tipe data yang hilang pada analisis dan hasilnya. Penelitian ini melakukan perbandingan dua teknik imputasi data: probabilistic principal component analysis (PPCA) dan multiple imputation using chained equations (MICE) (Hegde et al., 2019).

Penelitian ini menerapkan cara mengatasi data hilang dengan mengumpulkan, melacak data dengan hati-hati, dan menangani data hilang dengan mencari formulir yang hilang atau menghubungi kembali peserta studi. Tetapi pada kenyataannya di lapangan, pencegahan data hilang sangat sulit diatasi, sehingga diperlukan metode statistik untuk mengolaha daya yang hilang tersebut. Karena informasi yang hilang sangat kompleks, ahli statistik tidak mungkin merumuskan kumpulan pedoman universal yang berfungsi untuk semua situasi dan menjalankan simulasi untuk memprediksi solusi optimal (Sainani, 2015). Sehingga pada penelitian ini digunkan algoritma ekspetasi maksimisasi

(EM Algorithm) dengan membandingkan tiga metode klasifikasi data hilang yaitu, MCAR, MAR, dan MNAR untuk memperoleh estimasi terbaik dari ketiga metode klasifikasi tersebut.

Algoritma Ekspektasi Maksimisasi adalah algoritma umum yang digunakan untuk menghitung estimasi maksimum likelihood pada keadaan yang menyertakan pengamatan data data hilang. Algortima EM pertama kali diteliti secara sistematik oleh Dempster, Laird, dan Rubin (Gupta & Chen, 2010). Algoritma EM adalah proses dua langkah untuk mengestimasi parameter suatu model data tidak lengkap. Langkah awalnya adalah membagi data ke dalam dua bagian, yaitu bagian missing dan nonmissing, kemudian mengestimasi nilai data yang hilang melalui regresi linear sehingga data menjadi lengkap. Dimana regresi awal yang digunakan diambil dari data yang teramati saja, dengan syarat dapat meningkatkan parameter awal. Pada proses iterasi selanjutnya estimasi data hilang diperoleh dari persamaan regresi linear data lengkap pada data sebelumnya. Langkah akan terus berjalan sampai data yang hilang menjadi konvergen, sehingga didapatkan parameter yang maksimal. Berdasarkan keadaan tersebut, peneliti akan membahas metodologi algoritma ekspektasi maksimisasi untuk analisis maksimum likelihood pada model regresi linear dengan variabel independen berupa kategorik yang beberapa variabelnya terdapat data yang hilang dengan parameter constraint Pl +P⅛ + '" + Pi - ¹ = ⁰ . Selanjutnya peneliti membandingkan tiga metode klasifikasi data hilang. Metode yang dinyatakan baik adalah klasifikasi data hilang dengan tingkat kekonvergenan untuk iterasi paling sedikit dan kemudian menghitung tingkat kekonver-genan dengan menggunakan standar error missing information principle.

Langkah 1

Langkah 2

Langkah 3

Langkah 4

Langkah 5

Langkah 6

Langkah 7

Klasifikasi Data Hilang

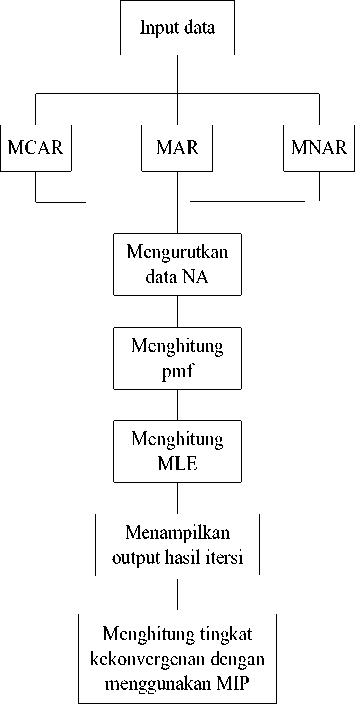
Gambar 1. Alur Kerja Program R

Berdasarkan Gambar 1 penelitian melakukan langkah satu sampai dengan langkah tujuh secara berurutan yang diawali dengan mengimput data dengan bantuan ms. excel. Langkah kedua pengklasifikasian data hilang menjadi tiga klasifikasi (MCAR, MAR, dan, MNAR). Adapaun tiga klasifikasi data hilang dihilangkan dengan mengasumsikan berapa banyak jumlah data yang akan dihilangkan, tidak ada batasan berapa banyak jumlah data yang akan dihilangkan, langkah ketiga mengurutkan data yang NA (Not Available) dari hasil klasifikasi data dengan memberikan nilai 1 (Satu) sebagai estimasi awal, langkah keempat menghitung pmf (probability mass function), langkah kelima melakukan estimasi dengan metode maksimum likelihood , langkah keenam menampilkan output berupa hasil iterasi, dan langkah terakhir melakukan perhitungan tingkat kekonvergenan dengan menggunakan Missing Information Principle (MIP):

∂²h(θ,θ) g-g ∂θ∂θ^t

8²in₃(γe') _  3∖⅛⅛)

--------z  '^--∑—

∂θ∂θ^t

₁ a⅛ dan ∂θ^z

∂θ∂θ^t

, dimana —     sebagai informasi lengkap

∣S=Θ

sebagai informasi yang hilang, jadi berdasarkan informasi utama yang hilang

(Louis, 1982) meyatkan bahwa Informasi yang teramati = Informasi lengkap – Informasi yang hilang (Harizahayu, 2014).

• 3.    Hasil dan Pembahasan

Data yang digunakan dalam kasus ini adalah data sekunder yang berasal dari lampiran penelitian skripsi dengan judul “Hubungan kualitas hidup terhadap terjadinya xerostomia pada orang yang merokok”. Variabel independent pada data ini adalah skor OHIP-14. Data skor OHIP diperoleh melalui penyebaran kuesioner kepada respodent perokok di sekitar wilayah Sungai durian, Koto panjang dalam, dan Perambahan (Erauly, 2014). Kesehatan gigi dan mulut terkait kualitas hidup dapat diukur dengan menggunakan tujuh dimensi dalam Oral Health Impact Profile -14 (OHIP-14) di mana tujuh dimensi tersebut (keterbatasan fungsi, rasa sakit fisik, ketidaknyamanan psikis, ketidakmampuan sosial, dan handikap) merupakan dampak akibat kualitas hidup. Xerostomia adalah perasaan subjektif dari mulut kering. Penyebab utamanya adalah sindrom Sjögren (SS), pengobatan dan radioterapi pada kepala dan leher. SS adalah penyakit au-toimun sistemik kronis yang ditandai dengan infiltrasi kelenjar eksokrin, khususnya kelenjar ludah dan lakrimal. Gangguan yang biasa ditemukan dalam praktik kedokteran gigi adalah xerostomia atau mulut kering (Cassolato & Turnbull, 2003). Tanda-tanda utama xerostomia termasuk kesan mulut kering , masalah dengan konsumsi makanan, dan kekeringan pada mukosa mulut dan kulit (Delli et al., 2014). Evaluasi didasarkan pada wawancara terstruktur (test Fox) dan penentuan volume saliva yang tidak distimulasi dan distimulasi (Tanasiewicz et al., 2016).

• 3.1.    Ilustrasi Data

Tujuan penelitian ini adalah menganalisis hubungan antara skor Oral Health Impact Profile (OHIP-14) dan umur terhadap kualitas hidup. OHIP-14 bertujuan untuk memprediksi dampak yang terkait dengan kondisi mulut secara umum, bukan dampak yang mungkin disebabkan oleh kelainan rongga mulut atau sindrom tertentu. Data yang digunakan dalam penelitian ini merupakan data lengkap dan tidak terdapat nilai data yang hilang, namun demi tujuan dari penelitian ini yakni mencari estimasi nilai data hilang dari analisis persamaan regresi sederhana. Maka data yang digunakan pada penelitian ini hanya sebagian sesuai dengan kebutuhan dan nilai data dari variabel umur akan dihilangkan. Berikut gambaran singkat mengenai data hasil penelitian. Penulis mengilustrasikan aplikasi dari model regresi linear sederhana dengan mengasumsikan relasi antara skor OHIP-14 (J^r) dan tipe perokok ringan, sedang, dan berat yang dinotasikan dengan 1 untuk perokok ringan, 2 untuk untuk perokok sedang, dan 3 untuk

perokok berat atau tipe perokok (X) ,(X = 1,2,3). Sehingga model regresi dapat dituliskan dalam persamaan Y = β₀ + β₁X + e .

3.2. Estimasi Nilai Data Hilang Menggunakan Algoritma EM

Dalam mencari nilai estimasi data hilang dengan menggunakan algoritma EM, terdapat beberapa langkah. Pada penelitian ini akan dilakukan dengan tiga metode klasifikasi data hilang yaitu, MCAR, MAR, dan MNAR. Adapun langkah-langkahnya adalah sebagai berikut:

Langkah I

membentuk klasifikasi dari tiga metode

Langkah 2

menentukan nilai inisialisasi awal dengan menggunakan anlisis regresi linear sederhana pada data pengamatan.

Langkah 3

melakukan analisis regresi linear pada data lengkap. Analisis ini dimaksudkan untuk memperoleh model awal regresi pada data dan melihat keeratan hubungan pada data pengamatan

Langkah 4

E (ekspektasi) dan M (maksimisasi) dengan bantuan software R.

Langkah 5

membandingkan hasil estimasi pada tiga klasifikasi data hilang

Gambar 2. Langkah-Langkah Estimasi Data Hilang Menggunakan Algoritma EM

Langkah awal yang dilakukan penulis pada penelitian ini adalah mengklasifikasikan data menggunkan tiga klasifikasi seperi Gambar 1, langkah kedua mencari nilai inisialisasi awal atau dengan menggunakan anlisis regresi linear sederhana. Langkah ketiga, sebelum melakukan anlisis regresi pada data yang tersedia maka akan dilakukan uji pada beberapa asumsi yang terkai dengan

analisis regresi linear sederhana. Uji asumsi tersebut adalah uji linearitas, uji normalitas data kualitas hidup dan uji kelayakan

model. Persamaan regresi yang diperoleh dari hasil analisis yaitu:

OHIP=11,867+1,5*Umur                (3.1)

Setelah diperoleh nilai dari persamaan estimasi regresinya, diperoleh nilai awal:

e'” - (^‰^,^.rf

= (11.867,0.539,0.333,0.333,0.333,6.881)          (3.2)

dengan

β(⁰: Nilai intersep regresi data pengamatan

β°⁰: Nilai koefisien umur pada regresi dengan data pengamatan

p⁽⁰⁾: Nilai peluang rata- rata p(⁽⁰⁾ + p⁽⁰⁾ + p⁽⁰⁾ = 1 σ^⁰): Standar deviasi '/

Langkah keempat adalah melakukan langkah E (ekspektasi) dan langkah M (maksimisasi) yang dilakukan dengan bantuan software R , dan langkah terakhir penulis membandingkan nilai-nilai hasil estimasi              dan dari dua klasifikasi data

MCAR, MAR, MNAR. Kemudian dibuat grafik perbandingan dengan bantuan program R.

• 3.3.    Membandingkan Hasil Estimasi pada Tiga Klasifikasi Data Hilang

Pada tahapan akan dibandingkan nilai-nilai hasil estimasi               dan

dari dua klasifikasi data MCAR, MAR, MNAR yang ditampilkan dengan menggunakan grafik. Grafik berfungsi untuk memberikan data yang lebih menarik, dapat mengetahui naik turunnya suatu keadaan data, dan menyajikan data yang dapat lebih mudah dipahami (Setyowati, 2019). Sehingga peneliti membuat grafik perbandingan dengan bantuan program R dan menampilkan grafik kekonvergenan algoritma EM sebagai berikut:

Gambar 3. Hasil Estimasi pada Tiga Klasifikasi Data Hilang

Berdasarkan grafik Gambar 3 dapat dilihat hasil estimasi^θ = (Λ∙βvPι∙PzP3>^σ^ dengan menggunakan tiga klasifikasi data hilang yaitu : MCAR, MAR, dan MNAR. E-

stimasi menggunakan Missing Completely at Random (MCAR) akan konvergen pada iterasi ke-13 dengan standar error 0,5143876, estimasi menggunakan Missing at Random akan konvergen pada iterasi ke-65 dengan standar error 0,6580985, sedangkan estimasi dengan menggunakan Missing Not at Random akan konvergen pada iterasi ke-383 dengan standar error 0,7939673. Jadi, berdasarkan kecepatan konvergensi dan standar error dapat diambil kesimpulan metode klasifikasi untuk data hilang dengan menggunakan algoritma EM untuk model regresi dengan parameter constraint adalah Missing Completely at Random (MCAR) lebih baik dari metode lainnya. Hal itu dapat dilihat dari grafik yang digambarkan, bahwa tingkat kekonvergenan Missing Completely at Random cenderung lebih stabil dibandingkan MAR dan MNAR. Untuk memperkuat bahwa MCAR lebih baik diantara ketiga klasifikasi data, akan diperlihatkan grafik perbandingan nilai data asli dengan nilai estimasi dari ketiga klasifikasi data.

Gambar 4. Grafik Perbandingan Data Asli dan Data Estimasi

Berdasarkan grafik Gambar 4 dapat dilihat bahwa nilai estimasi dari tiga klasifikasi data hilang, bahwa Missing Completely at Random (MCAR) mempunyai nilai yang sangat dekat dengan nilai asli.

Tabel 1. Perbandingan Hasil Analisis Regresi Data Asli dengan Estimasi

Model	⅛	.01	Pi	F⅛	eξ	sigma	mean
Data Asli	11,867	1,5	0,3333	0,3333	0,3333	1,2351	2
MCAR	11,079	2,074	0,4524	0,2818	0,2639	1,2796	1,8264
MAR	4,943	4,806	0,2811	0,3734	0,3455	2,5728	2,0646
MNAR	19,244	-1.947	0,2749	0,2540	0,4962	13,4507	0,2464

Berdasarkan Tabel 1 dapat terlihat bahwa hasil analisis regresi dengan nilai estimasi dan ketiga memiliki nilai yang hampir berdekatan. Sedangkan nilai estimasi MCAR memiliki nilai yang paling mendekati data asli. Hal ini menunjukkan bahwa hasil estimasi yang dilakukan dengan menggunakan algoritma Ekspektasi Maksimisasi dengan metode klasifikasi data hilang MCAR mendekati nilai data asli. Berdasarkan Grafik 1 sampai dengan Grafik 7 perbandingan data asli dan estimasi dan Tabel 1 perbandingan analisis regresi dengan nilai estimasi, maka dapat disimpulkan bahwa algoritma Ekspektasi Maksimisasi dengan menggunakan metode MCAR untuk data hilang menghasilkan estimasi yang baik dengan nilai estimasi 0,5143876 untuk konvergensi pada iterasi yang ke-13.

• 4.    Kesimpulan

Berdasarkan pembahasan penelitian yang telah dilakukan maka dapat disimpulkan bahwa data hilang merupakan suatu problem / masalah karena data yang hilang menyebabkan sulitnya interpretasi data. Masalah data yang hilang dapat diselesaikan dengan pendekatan klasifikasi data hilang dengan Missing Completely at Random (MCAR) yang merupakan klasifikasi terbaik dibanding dengan dua klasifikasi (MAR dan MNAR) karena memiliki estimasi yang hampir sama dengan nilai aslinya.

Daftar Pustaka

Allison, P. D. (2012). Handling Missing Data by Maximum Likelihood. SAS Global Forum 2012 Statistics and Data Analysis.

Angelini, C. (2018). Regression analysis. In Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics (Vols. 1–3). Elsevier Ltd. https://doi.org/10.1016/B978-0-12-809633-8.20360-9

Cassolato, S. F., & Turnbull, R. S. (2003). Xerostomia: clinical aspects and treatment. In

Gerodontology. https://doi.org/10.1111/j.1741-2358.2003.00064.x

Delli, K., Spijkervet, F. K. L., Kroese, F. G. M., Bootsma, H., & Vissink, A. (2014).

Xerostomia. Monographs in Oral Science. https://doi.org/10.1159/000358792

Gupta, M. R., & Chen, Y. (2010). Theory and use of the em algorithm. Foundations and

Trends in Signal Processing. https://doi.org/10.1561/2000000034

Erauly, Olga. (2014). Hubungan kulaitas hidup terhadap terjadinya xerostomia pada orang yang merokok. Skrip. Fakultas Kedokteran Gigi Andalas, Padang

Harizahayu. (2014). Estimasi Maksimu Likelihood Melalui Algoritma Ekspektasi Maksimisasi untuk Model Regresi Linear dengan Data Hilang , Tesis, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Gadjah Mada.

Hegde, H., Shimpi, N., Panny, A., Glurich, I., Christie, P., & Acharya, A. (2019). MICE vs PPCA: Missing data imputation in healthcare. Informatics in Medicine Unlocked. https://doi.org/10.1016/j.imu.2019.100275

Sainani, K. L. (2015). Dealing With Missing Data. PM and R. https://doi.org/10.1016/j.pmrj.2015.07.011

Setyowati, D. (2019). Pelatihan Membuat Grafik dalam Microsoft Excel untuk Pengolahan dan Penyajian Data. Jurnal Dharma Bakti-LPPM IST AKPRIND Yogyakarta.

Tanasiewicz, M., Hildebrandt, T., & Obersztyn, I. (2016). Xerostomia of various etiologies: A review of the literature. In Advances in Clinical and Experimental Medicine. https://doi.org/10.17219/acem/29375

115