Penyelesaian Positif Model Penyebaran Virus Ebola Antar Dua Wilayah

Jurnal Matematika Vol. 10, No.1, Juni 2020, pp. 44-52

Article DOI: 10.24843/JMAT.2020.v10.i01.p122

ISSN: 1693-1394

Penyelesaian Positif Model Penyebaran Virus Ebola antar Dua Wilayah

Awawin Mustana Rohmah

Jl. Airlangga No. 3 Sukodadi Lamongan Jawa Timur e-mail: awawin.emer@gmail.com

Dinita Rahmalia

Jl. Airlangga No. 3 Sukodadi Lamongan Jawa Timur e-mail: dinitarahmalia@unisda.ac.id

Abstract: A Model describing the epidemic spread of the Ebola virus disease in region 1 and region 2 can be formed in a mathematical model, one of which is the SEIR endemic model. To form a mathematical model it is necessary to know the phenomenon of the spread of the Ebola virus, namely the large number of infected populations in an area which is not only caused by infected individuals in one area but can be caused by individuals traveling from one region to another. In this case, the SEIR model is analyzed for existence and uniqueness. Before doing the Analyze, the SEIR model was simplified. Then Lipschitz was determined, so that an analysis of existence and uniqueness could be carried out. This shows that the SEIR model has a unique solution. Furthermore, a positive solution is determined in the model, to show that the SEIR model has a continuous and dynamic flow. Based on these results, it was found that the SEIR model in the spread of the Ebola virus had dynamic and a continuous flow.

Keywords: Analysis of Existence and Uniqueness, Dynamic and a continuous Flow, Lipschitz, SEIR model

Abstrak: Model epidemik yang menggambarkan penyebaran penyakit virus Ebola di wilayah 1 dan wilayah 2 dapat dibentuk dalam model matematika yang salah satunya adalah model endemik SEIR. Untuk membentuk model matematika perlu diketahui adanya fenomena penyebaran virus Ebola yaitu banyaknya populasi terinfeksi dalam suatu wilayah yang tidak hanya disebabkan oleh individu terinfeksi pada satu wilayah akan tetapi dapat disebabkan oleh individu yang melakukan perjalanan dari wilayah ke wilayah lain. Dalam hal ini, model SEIR dilakukan analisa eksistensi dan ketunggalan. Sebelum dilakukan Analia, dilakukan penyederhanaan model SEIR. Kemudian ditentukan lipschitz, sehingga dapat dilakukan analisa eksistensi dan ketunggalan. Hal ini menunjukkan bahwa model SEIR mempunyai penyelesaian dan tunggal. Selanjutnya ditentukan penyelesaian positif pada Model tersebut, untuk menunjukkan bahwa model SEIR memiliki aliran kontinu dan dinamis. Berdasarkan hasil tersebut diperoleh bahwa model SEIR dalam penyebaran virus Ebola memiliki penyelesaian dan tunggal serta aliran kontinu.

Kata Kunci: Analisa Eksistensi dan Ketunggalan, Aliran Dinamis dan Kontinu Lipschitz, Model SEIR

• 1.    Pendahuluan

Penyakit Ebola merupakan virus yang dapat menyebar melalui kontak langsung dengan individu melalui kulit rusat atau selaput lendir dengan darah, sekresi, organ atau cairan tubuh lain dari orang yang terinfeksi. Penyebaran dapat juga terjadi pada individu terinfeksi dengan benda yang terkontaminasi antara lain tempat tidur dan pakaian yang terkontaminasi dengan cairan. Penyebaran virus Ebola terjadi ketika masyarakat melakukan kontak langsung dengan masyarakat lain saat melakukan perjalanan antar wilayah. Virus tersebut memiliki masa inkubasi 2-21 hari. Sedemikian hingga fenomena yang terjadi dapat dimodelkan.

Model matematika merupakan salah satu metode yang dapat digunakan untuk mempelajari dinamika dan memprediksi perilaku dari penyebaran virus Ebola. Fenomena tersebut dimodelkan oleh persamaan diferensial dengan representasi waktu kontinu. Beberapa contoh model matematika yang digunakan untuk mengetahui penyelesaian model penyebaran virus Ebola antara lain model SI, SIS, SIR, SEIS, SEIR, dan se-bagainya.

Hariyanto, Widodo, B., dan Budi, I, Nyoman (2013) mengkonstruksi model pro-koalisi antara virus influenza dengan H5N1 yang menyerang hewan unggas dan manusia. Model tersebut dibentuk berdasarkan transisi dan perubahan genetik pada populasi individu serta dilakukan analisa co-eksistensi dari kedua tranmisi virus. Rohmah, A.W., Hariyanto, Imron. C (2016) mengkonstruksi dan menganalisa model penyebaran virus Ebola antar dua Negara (Guinea dan Sierra Leone). Model tersebut dilakukan untuk mengetahui pola penyebaran penyakit. Rohmah (2017) menentukan solusi postif pada Model SIR untuk mengetahui ketunggalan dan eksistensi serta solusi pada model tersebut.

Berbeda dengan penelitian sebelumnya, pada penelitian ini mengembangkan model matematika tipe SEIR yang menggambarkan transmisi penyebaran virus Ebola antar dua wilayah tanpa adanya subpopulasi yang dapat terinfeksi kembali. Penelitian ini dilakukan karena banyaknya subpopulasi terinfeksi dalam suatu wilayah yang tidak hanya disebabkan oleh individu pada satu wilayah tetapi dapat disebabkan oleh individu dari wilayah lain. Untuk mengetahui model penyebaran virus perlu dilakukan analisa. Analisa yang dapat dilakukan yaitu eksistensi dan ketunggalan penyelesaian model SEIR dengan menunjukkan konstanta Lipschitz, Analisa eksistensi dan ketunggalan dilakukan untuk mengetahui bahwa model memiliki penyelesaian dan tunggal serta penyelesaian positif. Sedemikian sehingga dapat diketahui bahwa sistem tersebut memiliki aliran kontinu.

• 2.    Metode Penelitian

Metode yang digunakan untuk mencapai tujuan pada penelitian ini adalah menyederhanakan model SEIR. Penyederhanaan model SEIR dilakukan untuk menekankan terjadinya evolusi pada subpopulasi yang diamati. Kemudian menentukan eksistensi dan ketunggalan pada model SEIR. Untuk menunjukkan eksistensi dan ketunggalan penyelesaian pada model SEIR, ditentukan konstanta Lipschitz k(t). Misal-kanAC≡Rdanf-.A→ Rdisebut fungsi Lipschitz jika terdapat K > O sedemikian hing-

ga:

Hf(*ι) -∕0₂)∣∣ ≤ Λ'∣∣x₁-x₂∣∣,Vx₁,x₂ ∈ .4

(Pangarapan, 2009).

Setelah diperoleh konstanta Lipschitz, selanjutnya menentukan penyelesaian positif pada masing masing model dan dapat ditunjukkan bahwa model SEIR memiliki aliran kontinu dan dinamis. Aliran kontinuT = (X,R,π) pada X , dimanaπ∙.X×R → X

adalah pemetaan kontinu sedemikian hingga τr(x, O) = X untuk semua x ∈ X dan π(π(x, t), s) = π(x, t + s) untuk semuaxEXdan t,s E R (Freedman dkk, 1993).

• 3.    Hasil dan Pembahasan
  
  3.1    Penyederhanaan Model SEIR

Langkah pertama sebelum dilakukan analisa eksistensi dan ketunggalan adalah

penyederhanaan model SEIR sehingga diperoleh

dS₁ dt dS₂ dt d E₁ dt

d E₂ dt dl₁ dt dl₂ dt dR₁ dt

d R₂ dt

λ₁S₁ — b.S, — (1 — p)S₁ — a₁S, + a₇S₇ — (1 — ρ)5₁

XX    XX '    • * X    XX    XiXi            X

λ₂5₂ — b₂S₂ — (1 — w)S₂ — Ct₂S₂ + α₁S₁ — (1 — y)S₂

pE₁ — (1 — n)E₁ — b. E₁ — a . E₁ + a₇E₇ + qE₁ * X      '          -^r X        X, X,        XX        Xi Xi           X

^w&2 ^— (1 ^{- c})¾ ^- ½¾ ^{- a}2^2 + ^al^l + y^2

nl₁ — b₁l₁ — (1 — fc)∕₁

^c⅞ ^- ½^2 ^- O ^{- u}^2

kR₁ — b₁R₁ — a₁R₁ + a₂R₂

uR₂ — b₂R₂- a₂R₂ + a₁R₁

• 3.2    Analisa Eksistensi dan Ketunggalan

Langkah selanjutnya adalah ditunjukkan eksistensi dan ketunggalan pada Model SEIR. Untuk menunjukkan eksistensi dan ketunggalan penyelesaiaan, ditentukan konstanta Lipschitz berikut.

ll∕(x¹(t),t) - /(x²(0,t)ll < It(I)IPr¹-X²II

Sehingga model SEIR berlaku untuk setiap f E R. Selanjutnya Persamaan (1) dapat dibentuk

dX , X

÷=λ*(o.o

Misalkan terdapat ∕σ¹(tM dan Λ*²ω,t) dengan

X¹ = ⅛, ^Z , ⅛ , ⅛ , ⅛ , ⅛ , ^i , ¾^t }

X² = {Sf, ^Z , ⅛ , ^Z , ∕₁ ,   , ^i ,    .

Selanjutnya akan dicari nilai dari k(t) yang merupakan konstanta Lipschitz dan memenuhi bentuk berikut.

ιι∕a^ι(o,t)-Λ*W)∣∣≤fc^^

dengan

∣∣Λ*W)-Λ*W)II =

^βll ^flZl ^α31 ^α41

dinyatakan sebagai «ii = ⅛ι + ς_i,

dengan

i = 1,2,3,4 maka

(2)

denganIIfe_ilII = maks∑‰ι Ife₁-I,dengan ketentuan «a ≤ IIfe₁₁II + l<ι<n ^{j j}

Berdasarkan Persamaan (1) dapat dibentuk sebegai berikut.

• 1.    Susceptible

«n =  f(S^t)-f(S^t)

α₁₁= ⅛-fe₁-(l-p)-(l-ρ))(Sι¹-Sj)

+ (^₂ - ½ - (1 - w) - (1 - y))(S∣ - 5²)

menggunakan ketentuan (2) maka diperoleh

Ilo₁IIl ≤ IIOi- ⅛1 - (1 -p) - (I - Q))(s₁¹ - Sf)∣∣ +

(3)

• ∣∣⅛ - ⅛ - (1 - _W) - (1 - y))(S* - s²)∣∣

  2. Exposed

  Cl_i∙ι =

  
  

  ^QZ1 ^-

  
  

  f(E},t)-f(E²_l,t)

  (p - (1 - n) - b₁ + q^) (⅛ -

  
  

  ^c) ½ + y)(⅛ ⅛)

  
  

menggunakan ketentuan (2) maka diperoleh

Ila₂₁Il < ||(p - (i - n) - b₁ + <j) (e₁¹ - ⅛)∣∣ +∣∣(w-(l-c)-b₂ + y)(⅛-l⅛)∣∣

(4)

• 3.    Infected

^clcl =

«31 ⁼

∕^,(z¹,t) - fC¹ι>^t)

(n - b₁ - (1 - fc))(Z₁¹ - Z₁²) + (c - b₂ - (1 - u))(Z¹ - Z₂²)

Menggunakan ketentuan (2) maka diperoleh

∣∣^α3i∣∣ ≤ Il(m - ^i - (i - ⅛))(z₁¹ - z₁²)∣∣ + IK^ ~ ½ ~ (1 ~ "))(Z₂¹ - ⅛)∣∣

(S)

• 4.    Removed

«ii = f(Rf_rt)-f(^,t)

«41 = (k - ^1) («f - Z?²) + (u - b₂) (ZZ₂¹ - Z?²)

Menggunakan ketentuan (2) maka diperoleh

Ila₄₁Il < IKfc- b₁)(R₁¹ -¾=)∣∣+∣∣(_b-⅛)(8₁¹-B≈)∣∣

(6)

Selanjutnya Persamaan (3) – (6) dapat dibentuk norm sebagai berikut.

IIΛ*W)-f(*W)∣∣ =

^flIl «21 «31 «41

= H ½ι +q_i Il

ll∕(x¹(t),t) -f(^²(0^)∣∣ ≤ l∣M + IlCiiII, sehingga

“11

«21

«31

«41

(λ₁ - b₁ - (1 - p) - (1 - q))(S₁¹ - S₁²)

(p - (1 - n) - b₁ + 7) (E₁¹ - E₁²)

(n-b₁ - (1 - fc))(Z₁¹ - Zf) (fc-b₁)(ZZ₁¹-Λ²)

(?)

U₂ - b₂ - (1 - w) - (1 - y))(S¹ - S²)

(w - (1 - c) - b₂ + y) (E₂¹ - E₂²)

(c - b₂ - (1 - u))(Z₂¹ - Z₂²)

(w-½) (Zl₂-ZJ₂)

Sehingga

ι∣yα^ιω.t) -∕α²ω.t)∣ι ≤ *ι(t)∣ι⅛₁ιι+*₂ωιι¾∣∣

Dengan demikian diperoleh konstanta Lipschitz k(t) di kedua wilayah tersebut adalah

(A₁ - b₁ - (1 - p) - (1 - _g))(S_i¹ - S₁²)+(A₂ - b₂ - (1 - w) - (1 - y))(S₂¹ - S²) (p - (1 - n) ~ b₁ + ρ)(E¹ - E₁²)      +(w - (1 - c) - b₂ + y)(E₂¹ - E₂²)

(n - b₁ - (1 - fc))(Z₁¹ - Z₁²)            +(c - b₂ - (1 - u))(Z₂¹ - Z₂²)

(fc-b₁) (ZZ¹-ZZf)                  +(u-b₂)(ZZ∣- E₂²)

≤ k₁(t)

(s₁¹-s₁≡) (e₁¹-e₁²) W-Zi²) (Zi₁¹ - ZZ₁²)

+ ^fez(C

(S₂¹-S₂²) (E₂¹-Ef) (Z₂¹-Z₂²) (Zl₂¹ - Zl₂²)

Individu infected hanya dapat menyebarkan virus di wilayahnya sendiri. Sedemikian hingga pengamatan hanya dilakukan pada subpopulasi infected di masing-masing wilayah. Dengan demikian nilai maksimum dari {fc₁(t)Λ₂(t)} merupakan konstanta Lipschitz di wilayah 1 dan wilayah 2. Konstanta Lipschitz mempunyai pengaruh sangat besar terhadap konstruksi model SEIR untuk setiap t E R ⁺ .

Dengan kl(t) ~ ∣((ⁿ)mαΛ- (⅛1÷(1 ^)_mt_n)l dan ^^c2(^t) ⁼ l((^c)mαx ^- (½ ÷ C¹ ~ ^u^)_min)l.

• 3.3    Penyelesaian Positif

Sebelum ditunjukkan bahwa sistem memiliki aliran kontinu dan dinamis, perlu dikonstruksi model mempunyai penyelesaian positif. Pada model matematika SEIR terjadi pergerakan pada setiap individu di wilayahnya sendiri maupun di wilayah lain. Dalam hal ini pergerakan yang terjadi di wilayahnya sendiri misalkan individu susceptible bergerak dan memiliki peluang bertemu dengan individu infected, sehingga mengakibat terjadinya transmisi virus dan mengakibatkan terjadinya perubahan status dari individu susceptible menjadi individu exposed. Untuk pergerakan yang terjadi antar wilayah misalkan individu susceptible di wilayah 1 melakukan perjalanan ke wilayah 2 dan individu susceptible berhubungan kontak langsung dengan individu exposed,dan juga sebaliknya untuk wilayah 2.

Perubahan dinamis yang terjadi pada konstruksi model matematika ditunjukkan oleh perubahan status individu terhadap virus yang disebabkan oleh transmisi virus, karena untuk menunjukkan bahwa konstruksi model merupakan sistem dinamis, pengamatan ditujukan pada dinamika virus yang dapat dilihat pada model sistem. Selanjutnya ditentukan total populasi pada masing-masing wilayah dari Persamaan (1) dan ditentukan penyelesaiannya.

Pada model wilayah 1 terdapat subpopulasi susceptible, exposed, removed dari wilayah 1 yang melakukan perjalanan ke wilayah 2 tetapi juga terdapat subpopulasi susceptible, exposed, removed dari wilayah 2 yang melakukan perjalanan ke wilayah 1. Diasumsikan bahwa individu dari wilayah 1 yang melakukan perjalanan ke wilayah 2 dengan proporsi sebesar S₁ dan individu dari wilayah 2 yang melakukan perjalanan ke wilayah 1 dengan proporsi sebesar d 2, dimana subpopulasi infected terbatas, tidak dapat melakukan perjalanan ke wilayah lain. Sedemikian hingga proporsi subpopulasi susceptible, exposed, removed yang berasal dari wilayah 1 yang melakukan perjalanan ke wilayah 2 O₁(JV₁-J₁))adalah S₁JV₁. Untuk proporsi subpopulasi susceptible, exposed, removed yang berasal dari wilayah 2 yang melakukan perjalanan ke wilayah 1 ⅛-⅛)adalah S₂N₁ .

Untuk model wilayah 2 terdapat subpopulasi susceptible, exposed, removed dari wilayah 2 yang melakukan perjalanan ke wilayah 1 tetapi juga terdapat subpopulasi susceptible, exposed, removed dari wilayah 1 yang melakukan perjalanan ke wilayah 2. Diasumsikan bahwa individu dari wilayah 2 yang melakukan perjalanan ke wilayah 1 dengan proporsi sebesar ^ 3 dan individu dari wilayah 1 yang melakukan perjalanan ke wilayah 2 dengan proporsi sebesar ^4, dimana subpopulasi infected terbatas, tidak dapat melakukan perjalanan ke wilayah lain. Sedemikian hingga proporsi subpopulasi susceptible, exposed, removed yang berasal dari wilayah 1 yang melakukan perjalanan ke wilayah 2 O₂Gv₂-⅞)) adalah δ₃N₂. Untuk proporsi subpopulasi susceptible, exposed, removed yang berasal dari wilayah 2 yang melakukan perjalanan ke wilayah 1 (a₁(N₁-Z₁))adalah S₄N₂ .

Oleh karena itu total populasi untuk wilayah 1 adalah sebagai berikut.

dN₁ dt

dS, dE. di. dR.

—--—¹ + -+ —-

dt dt dt dt

= a₁N₁ - b₁N₁ - δ₁N₁ + δ₂N

Sedemikian hingga dapat ditulis sebagai berikut.

dN₁ dt

a₁N₁ - b₁N₁ - δ₁N₁ + δ₂N

(S)

Sehingga penyelesaiannya untuk Persamaan (8) adalah

dN₁ dt

f ^dNi

1∏∣N₁∣

(α₁ - b₁ - 5₁ + δ₂)N

(a₁ — b₁ — 5₁ ÷ δ₂)dt

(a₁ — b₁ — δ₁ + <

Ce^^aι^-6ι^-5χ^+δz)^r

Selanjutnya ditentukan nilai konstanta C dengan t = O sehingga

TV₁(O) =     _ce(a₁-b₁-5₁+δ_s)t

C    =    N₁(O)

Kemudian nilai C disubstitusikan ke ^l C^ sehingga

N₁(f)

N₁(0)e^ι^-bι^-^^+,s≈^k

Pada saat t → ∞ diperoleh

Iim N₁ (t) =    lim(N,(0)e^ca^^^-^^+δ=*^t

r→∞            t→∞^{v i}

Sehingga N -^ (^ merupakan penyelesaian positif.

Untuk wilayah 2 adalah sebagai berikut.

d N₂ dt

dS₂ dE₂ dl₂ dR₂

dt    dt    dt   dt

a^N, - b^N₂ + δ.N₇ - δ.N, 4rfb                          it        t it

Sehingga dapat ditulis sebagai berikut.

a₇N₇ - b₇N₇ + δ.N₇ - δ.N,

Sedemikian hingga penyelesaian Persamaan (9) adalah

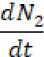
InRv₂I

(^α2 ½ + ^ 3 $4)^2

j' (^α2 ^- ⅛ + ®3 ^- ^4)^ (α₂-b₂+S₃-5₄)t+c ^_e{^az~^b^^sι~^si)^t

Selanjutnya ditentukan nilai konstanta C dengan t = O sehingga

N₂(O) =    _ce(α_s→_s+5_s-5₄)t

C =    N₂(O)

Kemudian nilai C disubstitusikan ke ^j^ 2 C ^ sehingga

N₂ (t) =    N₂(0)e^cα≈^^b≡⁺⁵*^^^t

Pada saat t → ∞ diperoleh

N₂ (t) =    N₂(0)e^ca≈^^b≡⁺⁵*^^^t

Sehingga ^j^2 C O merupakan penyelesaian positif.

Berdasarkan model SEIR tersebut, setiap perubahan subpopulasi dalam total populasi N terhadap waktu (t) ada yang monoton naik dan monoton turun. Sedemikian hingga model tersebut memiliki aliran sistem dinamis.

• 4.    Kesimpulan dan Saran

Berdasarkan hasil penelitian tersebut, diperoleh bahwa model SEIR mempunyai penyelesaian dan tunggal, serta mempunyai penyelesaian positif dan aliran model tersebut dinamis.

Ucapan Terima Kasih

Penulis mengucapakan terimakasih kepada Kementerian Pendidikan dan Kebudayaan Tinggi bidang Riset dan Pengabdian Kepada Masyarakat, karena telah diberikan pendanaan pada Artikel ilmiah ini, yang merupakan luaran dari penelitian dosen pemula tahun 2019.

Daftar Pustaka

• [1]    Freedman, H. I., Ruan, S., dan Tang, M. 1993. Uniform Persistence and Sub Flows Near a Closed Positively Invariant Set. Journal of Dynamics and Differential Equation 6(2).

• [2]    Hariyanto, W. Basuki, Budiantara, I Nyoman. 2013. The Construction of a Model Pre-Coalition between H1N1-p and H5N1 Influenza Virus in Indonesia. Applied Mathematical Sciences, Hikari Ltd Vol 7, p. 4899-4907.

• [3]    Pangarapan, L.S. 2009. Analisa Persoalan Optimasi Konveks Dua Tahap. Tesis. Universitas Sumatra.

• [4]    Rohmah, A.M. 2017. Solusi Postif Model SIR. Unisda Journal Mathematics and Computer Science 3(1), p. 21-28.

• [5]    Rohmah, A.M., Hariyanto, C. Imron. 2016. Persitence Analyze of The Spreading Ebola Virus between Two Countries. Proceeding of The 6^th Annual Basic Science International Conference, p. 354-357.

52