Penerapan Jaringan Syaraf Tiruan Dalam Pembentukan Model Peramalan Angka Melek Huruf di Kabupaten Karangasem
on
Jurnal Matematika Vol. 10, No.1, Juni 2020, pp 11-21
Article DOI: 10.24843/JMAT.2020.v10.i01.p119
ISSN: 1693-1394
Penerapan Jaringan Syaraf Tiruan Dalam Pembentukan Model Peramalan Angka Melek Huruf di Kabupaten Karangasem
I Gusti Ngurah Lanang Wijayakusuma§
Program Studi Matematika, Fakultas MIPA, Universitas Udayana e-mail: lanang_wijaya@unud.ac.id
Ni Kadek Emik Sapitri
Program Studi Matematika, Fakultas MIPA, Universitas Udayana e-mail: emikpritri@gmail.com
§ Penulis Korespondesi
Abstract: Literacy rate (AMH) is one component of the human development index (HDI). Referring to the data of the Central Bureau of Statistics (BPS) of Bali Province 2018, AMH Karangasem Regency in 2018 has the lowest value of 84.91 percent. This value is quite far compared to AMH Denpasar City which almost reached 100 percent, to be exact 98.02 percent. Thus, it is important to create a model that can predict AMH values in Karangasem Regency in the coming year. This study uses data on Poor Population Percentage (PPM) and School Participation Rate (APS) in Karangasem Regency in 2007 s. 2018 as input and AMH Karangasem Regency in 2007 s. 2018 as output. After being processed using the backpropagation algorithm, the minimum overfitting model is obtained, namely the 2-5-1 model with an average error per iteration of 0.00049386.
Keywords: Literacy rate, backpropagation, overfitting
Abstrak: Angka melek huruf (AMH) adalah salah satu komponen indeks pembangunan manusia (IPM). Mengacu pada data Badan Pusat Statistik (BPS) Provinsi Bali 2018, AMH Kabupaten Karangasem pada 2018 memiliki nilai terendah 84,91 persen. Nilai ini cukup jauh dibandingkan dengan AMH Kota Denpasar yang hampir mencapai 100 persen, tepatnya 98,02 persen. Oleh karena itu, penting untuk membuat model yang dapat memprediksi nilai AMH di Kabupaten Karangasem di tahun mendatang. Penelitian ini menggunakan data Persentase Penduduk Miskin (PPM) dan Angka Partisipasi Sekolah (APS) di Kabupaten Karangasem pada tahun 2007 s. 2018 sebagai input dan AMH Kabupaten Karangasem pada tahun 2007 s. 2018 sebagai output. Setelah diproses menggunakan algoritma backpropagation, model overfitting minimum diperoleh, yaitu model 2-5-1 dengan kesalahan rata-rata per iterasi 0,00049386.
Kata Kunci: Angka melek huruf, backpropagation, overfitting.
Kabupaten Karangasem terletak di ujung timur Pulau Bali. Setiap kabupaten atau kota termasuk Kabupaten Karangasem mempunyai data indeks pembangunan manusia (IPM). IPM merupakan indeks komposit dari tiga komponen, yaitu Produk Domestik Regional Bruto (PDRB) per kapita, angka harapan hidup, dan tingkat pendidikan penduduk. Komponen tingkat pendidikan penduduk tersebut mencakup angka melek huruf, rata-rata lama sekolah, dan persentase pendidikan yang ditamatkan (Sudibia & Marhaeni, 2012).
Berdasarkan Sistem Rujukan Statistik (Sirusa) Badan Pusat Statistik (BPS), Angka Melek Huruf (AMH) adalah proporsi penduduk usia 15 tahun ke atas yang mempunyai kemampuan membaca dan menulis huruf latin dan huruf lainnya (tanpa harus mengerti apa yang di baca atau ditulisnya) terhadap penduduk usia 15 tahun ke atas. AMH dapat menjadi indikator untuk mengetahui perkembangan pendidikan penduduk, sebab semakin tinggi angka melek huruf atau kecakapan baca tulis, maka semakin tinggi pula mutu dan kualitas SDM (Dores & Jolianis, 2014). AMH merupakan indikator dasar karena membaca merupakan dasar utama dalam memperluas ilmu pengetahuan (Sudibia, et al., 2015).
Mengacu pada data Badan Pusat Statistik (BPS) Provinsi Bali (2018), AMH Kabupaten Karangasem pada tahun 2018 memiliki nilai paling rendah yaitu 84,91 persen. Nilai ini cukup jauh dibandingkan AMH Kota Denpasar yang hampir mencapai 100 persen, tepatnya 98,02 persen. Nilai AMH Kabupaten Karangasem ini menyatakan bahwa 15,09 persen penduduk umur 15 tahun ke atas di Kabupaten Karangasem tidak bisa baca-tulis huruf latin atau huruf lainnya. Oleh karena itu, penting untuk membuat suatu model yang dapat memprediksi nilai AMH di Kabupaten Karangasem pada tahun yang akan datang.
Pada penelitian sebelumnya, Fadila, et.al., (2015) menduga AMH di Kabupaten Bangkalan menggunakan Small Area Estimation dengan Pendekatan Hierarchical Bayes. Diperoleh rata-rata AMH untuk seluruh kecamatan di Kabupaten Bangkalan adalah 72,92 persen dengan standar deviasi sebesar 0,0832. Selain itu, Simbolon, et.al., (2018) melakukan prediksi presentase penduduk buta huruf di Indonesia untuk 3 tahun ke depan, yakni tahun 2018-2020 dengan menggunakan Jaringan Syaraf Tiruan dengan algoritma Backpropagation arsitektur 4-14-1. Prediksi yang diperoleh memiliki akurasi 91 persen.
Pada studi ini, penulis hendak memanfaatkan jaringan syaraf tiruan (JST) untuk membuat model yang nantinya dapat digunakan untuk memprediksi AMH di Kabupaten Karangasem. Persentase Penduduk Miskin (PPM) dan Angka Partisipasi Sekolah (APS) per tahunnya akan digunakan sebagai data input. Rumusan masalah dari studi ini adalah bagaimana model arsitektur jaringan yang paling tepat untuk memprediksi AMH di Kabupaten Karangasem. Sementara itu, tujuan yang hendak dicapai adalah mendapatkan
model terbaik untuk memprediksi AMH di Kabupaten Karangasem berdasarkan data PPM dan APS.
Pada penelitian ini, data-data yang diperlukan dalam pembentukan model peramalan AMH di Kabupaten Karangasem diperoleh melalui laman situs BPS Provinsi Bali. Data tersebut mencakup data PPM, APS, dan AMH dari tahun ke tahun. Data yang telah diperoleh akan digunakan untuk membentuk model arsitektur JST yang dapat digunakan untuk meramalkan persentase AMH untuk tahun-tahun berikutnya. Setiap model yang terbentuk akan melalui proses pelatihan dan pengujian untuk meminimalisasi overfitting sehingga hasil peramalan nantinya akan lebih akurat.
Metode penelitian ini terdiri dari beberapa tahap seperti diperlihatkan pada Gambar 1.
Gambar 1. Diagram Alir Metode Penelitian
Data yang digunakan dalam penelitian ini dihimpun dari BPS Provinsi Bali. Data yang digunakan terdiri atas data PPM, APS, dan AMH di Kabupaten Karangasem pada tahun 2007 sampai dengan tahun 2018.
Metode normalisasi yang digunakan dalam penelitian ini adalah metode scalling dengan cara melakukan rescale data dari suatu range ke range baru. Data akan ditransformasi ke dalam range 0 dan 1 dengan cara membagi setiap data dengan nilai maksimum yang dapat dicapai atau dengan nilai terbesar pada kategori yang bersangkutan. Jika diberikan nilai yang bersesuaian (dalam satu kolom) {Xfc}; k = 1,2,3,..., n, maka nilai normalisasinya adalah:
r =(1) max{Xk}
di mana X' menyatakan data setelah dinormalisasi, X menyatakan data sebelum dinormalisasi.
Jaringan saraf tiruan merupakan sebuah model matematika, yang terdiri atas input layer, hidden layer, dan output layer. Pada kasus ini digunakan data PPM dan APS tahun 2007 sampai 2018 sebagai data input, dan nilai AMH sebagai output-nya.
Pada penelitian ini, akan digunakan satu lapisan hidden yang terdiri dari beberapa unit hidden. Pemilihan banyak unit hidden merupakan sebuah proses trial and error yang berbeda-beda untuk setiap kasus jaringan saraf tiruan. Oleh karena itu, akan dilakukan proses pelatihan dan pengujian untuk beragam jumlah unit hidden, yaitu 1, 2, 3, 4, dan 5. Galat yang diperoleh selama proses trial and error akan diminimalisasi dengan menggunakan algoritme backpropagation.
Algoritme backpropagation meliputi tiga tahap. Tahap pertama adalah feedforward. Tahap ini bergerak maju dari lapisan input sampai lapisan output dengan menggunakan fungsi aktivasi yang telah ditentukan. Tahap kedua adalah backward. Pada tahap ini, selisih antara output dengan target yang diinginkan merupakan kesalahan yang terjadi. Kesalahan tersebut dipropagasikan mundur, mulai dari garis yang terhubung langsung dengan setiap unit pada lapisan output. Kemudian tahap yang ketiga adalah tahap yang akan memodifikasi bobot untuk menurunkan tingkat kesalahan yang terjadi. Berikut adalah langkah dari algoritma Backpropagation dengan menggunakan software Jupiterlab dengan bahasa pemrograman Python (Welch, 2015):
Tahap Pertama : Propagasi maju (Forward)
Langkah 0 : Inisialisasi semua bobot dengan bilangan acak
Langkah 1 : Jika kondisi penghentian belum terpenuhi, lakukan langkah 2-11
Langkah 2 : Untuk setiap pasangan data pelatihan lakukan langkah 3-9
Langkah 3 : Tiap unit masukan menerima sinyal dan meneruskannya ke unit tersembunyi di atasnya
Langkah 4 : Hitunglah semua output di unit tersembunyi tersebut. Perhatikan rumus no.[2] :
z(2) = χιyCD
(2)
dengan X menyatakan matriks data input dan klΛD menyatakan matriks bobot dari input layer ke hidden layer.
Langkah selanjutnya adalah menerapkan fungsi aktivasi pada z(2) sehingga di dapat rumus sebagai berikut :
(3)
^' ■' :.^
dengan f(x) merupakan fungsi aktivasi yang dalam kasus ini dipilih fungsi sigmoid biner.
Langkah 5 : Hitunglah semua keluaran jaringan di unit dengan mengalikan hasil sebelumnya dengan bobot sehingga di dapat rumus sebagai berikut:
z(3) = α(2)ιy(2)
(4)
(5)
dengan ^(2) menyatakan matriks bobot dari hidden layer ke output layer.
Sehingga selanjutnya di dapatlah hasil prediksi (y) sebagai berikut:
1
' )
Pada akhir langkah 5, sudah dapat kita dapatkan hasil peramalan. Namun hasil yang di dapatkan sangat tidak akurat atau memiliki error yang cukup besar. Oleh karena itu, diperlukan pelatihan terhadap model neural network yang kita dapatkan agar mendapatkan hasil yang lebih akurat.
Tahap Kedua : Propagasi Mundur
Langkah 6 : Menghitung error dari hasil yang sebelumnya kita dapat dengan costfunction dengan rumus:
(6)
(7)
^=∑∣(y-y)2
. Langkah 7 : Mengubah bobot dengan mendiferensialkan J sehingga didapat:
—^_ = (αC2Dτ5(3)
∂W(2) (“ ) 0
dimana δ(3 = -(y — y) f'(z(3^^ (8)
∂J ∂W(1
= Xτδ(2
dimana δ(3 = δ(3)(W(2))τf'(z(2))
(9)
(10)
Dengan pangkat T menyatakan transpose matriks.
Dari akhir langkah ini kita akan dapatkan bobot sehingga galat dari model neural network yang kita buat semakin kecil.
Tahap Ketiga : Pelatihan Neural Network
Langkah 8 : Melakukan langkah propagasi maju dan propagasi mundur kembali dengan bobot yang didapatkan dari tahap kedua. Pada langkah ini dapat kita peroleh perubahan J terhadap W yang baru sehingga mendapatkan nilai cost function yang minimal
Langkah 9 : Menguji apakah kondisi berhenti sudah terpenuhi. Kondisi berhenti ini terpenuhi jika nilai kesalahan yang dihasilkan lebih kecil dari nilai kesalahan referensi.
Tahap Keempat : Menghitung tingkat akurasi peramalan
Langkah 10: Melakukan Regularisasi
Regularisasi pada dasarnya menambah penalti saat kompleksitas model meningkat. Parameter regularisasi (lambda) menghindarkan semua parameter kecuali intersep sehingga model menggeneralisasi data dan tidak akan terjadi overfitting (Nagpal, 2017). Langkah 11: Memilih arsitektur JST
Untuk memilih arsitektur JST yang paling tepat, akan dipilih arsitektur JST dengan rata-rata error per iterasi terkecil. Rata-rata error per iterasi dihitung dengan rumus:
Rata-rata error per-iterasi = 1∑i=1 Ui — testJi | (11)
di mana n menyatakan banyak iterasi, Ji menyatakan nilai costFunction pada iterasi ke-i untuk data latih, dan testJi menyatakan nilai costFunction pada iterasi ke-i untuk data uji.
Data PPM, APS, dan AMH di Kabupaten Karangasem pada tahun 2007 sampai dengan tahun 2018 yang diperoleh dari BPS Provinsi Bali adalah sebagai berikut:
Tabel 1. Data Penelitian
|
Tahun |
X1 : Persentase Penduduk Miskin (Persen) |
X2 : Angka Partisipasi Sekolah (Persen) |
Y : Angka Melek Huruf (Persen) |
|
2007 |
8.95 |
52 |
72.14 |
|
2008 |
7.67 |
50.60 |
70.82 |
|
2009 |
6.37 |
43.20 |
71.88 |
|
2010 |
7.95 |
53.71 |
72.40 |
|
2011 |
6.43 |
66.62 |
73.47 |
|
2012 |
5.63 |
52.45 |
77.41 |
|
2013 |
6.88 |
71.54 |
79.15 |
|
2014 |
7.3 |
77.23 |
79.11 |
|
2015 |
7.44 |
72.88 |
82.52 |
|
2016 |
6.61 |
66.74 |
81.74 |
|
2017 |
6.55 |
71.61 |
81.80 |
|
2018 |
6.28 |
80.11 |
84.91 |
Sumber: BPS 2018
Untuk mendapatkan data normalisasi dengan range 0 dan 1, perlu di normalisasi dengan metode Scalling yaitu dengan rumus:
_ X
(12)
(13)
Xnorm = ∣θθ
Y
Y _ =-- l norm ∣θθ
Sehingga di dapat hasil normalisasi sesuai Tabel 2.
Tabel 2. Hasil Normalisasi
|
Tahun |
X1 |
X2 |
Y |
|
2007 |
0.0895 |
0.52 |
0.7214 |
|
2008 |
0.0767 |
0.506 |
0.7082 |
|
2009 |
0.0637 |
0.432 |
0.7188 |
|
2010 |
0.0795 |
0.5371 |
0.724 |
|
2011 |
0.0643 |
0.6662 |
0.7347 |
|
2012 |
0.0563 |
0.5245 |
0.7741 |
|
2013 |
0.0688 |
0.7154 |
0.7915 |
|
2014 |
0.073 |
0.7723 |
0.7911 |
|
2015 |
0.0744 |
0.7288 |
0.8252 |
|
2016 |
0.0661 |
0.6674 |
0.8174 |
|
2017 |
0.0655 |
0.7161 |
0.818 |
|
2018 |
0.0628 |
0.8011 |
0.8491 |
Arsitektur jaringan yang terdiri dari tiga lapisan, yaitu lapisan input, lapisan tersembunyi, dan lapisan output. Pada kasus ini, Persentase Penduduk Miskin (PPM) dan Angka Partisipasi Sekolah (APS) sebagai input dan AMH sebagai output.
Pada penelitian ini, akan digunakan satu lapisan hidden yang terdiri dari beberapa unit hidden. Pemilihan banyak unit hidden sulit ditentukan. Oleh karena itu, akan dilakukan proses pelatihan dan testing untuk beragam jumlah unit hidden, yaitu 1, 2, 3, 4, dan 5. Selanjutnya jumlah unit hidden yang bervariasi tersebut yang akan dicoba-coba untuk didapatkan hasil yang baik atau hasil yang optimal.
Model yang baik dapat dilihat dari nilai costFunction pelatihan yang kecil. Tabel 3 merupakan hasil cost dari proses pelatihan dan testing dengan menggunakan metode Backpropagation dengan unit hidden sebanyak 1 sampai 5 unit hidden. Data pelatihan diambil dari data tahun 2017 sampai 2015 sedangkan untuk data uji digunakan data pada tahun 2016 hingga 2018. Diperoleh hasil sesuai Tabel 3:
Tabel 3. Hasil Percobaan Berbagai Jumlah Hidden Unit

Jumlah
hidden
Plot sebelum tahap regularisasi
Plot setelah tahap regularisasi
unit

Jumlah iterasi: 96

Jumlah iterasi: 55
Rata-rata error per-iterasi: 0.00075598
Rata-rata error per-iterasi: 0.00093183


Jumlah iterasi: 119 Rata-rata error per-iterasi: 0.00051987
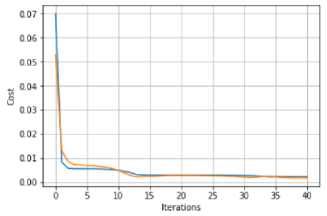
Jumlah iterasi: 41
Rata-rata error per-iterasi:
0.00113598
Jumlah iterasi: 69
Rata-rata error per-iterasi: 0.00050265

Jumlah iterasi:
Rata-rata error per-iterasi: 0.00065543

Garis biru di setiap grafik pada tabel no.[3] merujuk pada data latih dan garis merah pada data uji. Setelah dilakukannya pelatihan dengan jumlah hidden unit yang berbeda, didapatkan arsitektur dengan rata-rata error terkecil setelah proses regularisasi yaitu arsitektur dengan jumlah hidden unit 5 dengan rata-rata error 0.00049386. Oleh karena, itu didapat arsitektur (2-5-1) sesuai dengan gambar no.[2]:

Gambar 2. Arsitektur JST 2-5-1
Penelitian ini bertujuan untuk mendapatkan model terbaik untuk memprediksi AMH di Kabupaten Karangasem berdasarkan data PPM dan APS. Data yang digunakan yaitu data PPM, APS, dan AMH di Kabupaten Karangasem pada tahun 2007 sampai dengan tahun 2018 yang diperoleh dari BPS Provinsi Bali. Setelah diproses menggunakan JST algoritma backpropagation, diperoleh model dengan overfitting paling minimal yaitu arsitektur 2-5-1 dengan rata-rata error per iterasi sebesar 0.00049386.
Arsitektur JST yang diperoleh belum bisa disimpulkan sebagai arsitektur terbaik untuk memprediksi AMH dikarenakan masih minimnya data yang diperoleh dari BPS dan sedikitnya faktor yang dipertimbangkan. Oleh karena itu, pada penelitian selanjutnya disarankan untuk menambah jumlah input dengan mempertimbangkan faktor-faktor selain PPM dan APS, serta menambah jumlah data apabila data yang diperlukan sudah diperbaharui oleh BPS.
Daftar Pustaka
-
[1] Badan Pusat Statistik (BPS). (n.d.). Sistem Rujukan Statistik (Sirusa): Angka Melek Huruf (AMH). Retrieved April 7, 2019, from https://sirusa.bps.go.id/index.php?r=indikator/view&id=313
-
[2] Badan Pusat Statistik (BPS). (2018a). Angka Partisipasi Sekolah (APS) Provinsi Bali Menurut Kelompok Umur Pendidikan dan KabupatenKota, 2000-2018.
-
[3] Badan Pusat Statistik (BPS). (2018b). Persentase Penduduk Miskin Provinsi Bali Menurut Kabupaten atau Kota.
-
[4] Badan Pusat Statistik Provinsi Bali. (2018). Angka Melek Huruf (AMH) Penduduk Usia 15 Tahun Keatas Provinsi Bali Menurut Kabupaten/Kota, 2007-2018.
-
[5] Dores, E., & Jolianis. (2014). Pengaruh Angka Melek Huruf Dan Angka Harapan Hidup Terhadap Jumlah Penduduk Miskin Di Propinsi Sumatera Barat.
Economica (Journal of Economic and Economic Education), 2(2), 126–133. https://doi.org/10.22202/economica.2014.v2.i2.225
-
[6] Fadila, R., Rumiati, A. T., & Iriawan, N. (2015). Pendugaan Angka Melek Huruf di Kabupaten Bangkalan Menggunakan Small Area Estimation Dengan Pendekatan Hierarchical Bayes. Statistika, 3(2), 36–43.
-
[7] Nagpal, A. (2017). Over-fitting and Regularization – Towards Data Science. Retrieved May 13, 2019, from https://towardsdatascience.com/over-fitting-and-regularization-64d16100f45c
-
[8] Simbolon, I. A. R., Yatussa’ada, F., & Wanto, A. (2018). Penerapan Algoritma Backpropagation dalam Memprediksi Persentase Penduduk Buta Huruf di Indonesia. Jurnal Informatika Upgris, 4(2), 163–169.
https://doi.org/10.26877/jiu.v4i2.2423
-
[9] Sudibia, I. K., & Marhaeni, A. A. I. N. (2012). Beberapa Strategi Pengentasan Kemiskinan Di Kabupaten Karangasem, Provinsi Bali. PIRAMIDA, IX(1), 1–14.
-
[10] Sudibia, I. K., Marhaeni, A., Manuati Dewi, I. G. A., & Dayuh Rimbawan, I. N. (2015). Profil Kuantitas dan Kualitas Penduduk Provinsi Bali Tahun 2015. Bali.
-
[11] Welch, S. (2015). Neural Networks Demystified. Retrieved May 12, 2019, from https://github.com/stephencwelch/Neural-Networks-Demystified
21
Discussion and feedback