Estimasi Dampak Jangka Panjang Kebijakan Penurunan Emisi Terhadap Pertumbuhan Ekonomi Kalimantan Timur
on
Jurnal Matematika Vol. 9, No.1, Juni 2019, pp. 35-49 ISSN: 1693-1394
Article DOI: 10.24843/JMAT.2019.v09.i01.p109
Estimasi Dampak Jangka Panjang Kebijakan Penurunan Emisi Terhadap Pertumbuhan Ekonomi Kalimantan Timur
Nurul Ilma Hidayanty
Prodi Matematika, Institut Teknologi Kalimantan e-mail: 02151015@itk.ac.id
Riki Herliansyah
Prodi Matematika, Institut Teknologi Kalimantan e-mail: rikiherliansyah@itk.ac.id
Muhammad Azka
Prodi Matematika, Institut Teknologi Kalimantan e-mail: muhammad.azka@itk.ac.id
Abstract: Deforestation and forest degradation issue due to economic activity is a major problem in East Borneo. The results of data analysis from Environmental Agency stated East Borneo produced the biggest ammount of carbon dioxide (CO2) emissions after the Central Borneo and Riau. These emissions mostly come from land-based business sector, industry and transportation. In other side, these sectors are the highest contributor to the total number of Gross Domestic Regional Product (GDRP). The aim of this research is to identify the effect of the goverment policy to decrease CO2 emissions towards economic growth. The data in this research were analysed using Principal Component Analysis (PCA) and Path Analysis (PA). The results showed that the decrease in the sum of CO2 emissions resulting in decrease in the sum of GDRP.
Keywords: CO2 Emissions, Gross Domestic Regional Product (GDRP), Principal Component Analysis, Path Analysis.
-
1. Pendahuluan
Pembangunan ekonomi merupakan serangkaian proses usaha pembentukan pola kemitraan antara pemerintah, masyarakat maupun pihak swasta dalam mengelola sum-berdaya alam yang tersedia sehingga mampu menciptakan lapangan kerja baru. Tujuan pembangunan ekonomi yaitu untuk merangsang peningkatan taraf hidup masyarakat dengan cara mengusahakan agar pendapatan masyarakat terus naik dan disertai dengan tingkat pemerataan pendapatan yang sebaik mungkin. Ukuran keberhasilan pembangunan ekonomi dapat dilihat dari tingginya tingkat pencapaian pertumbuhan
ekonomi. Produk Domestik Regional Bruto (PDRB) menjadi salah satu tolak ukur tingkat pertumbuhan ekonomi daerah baik dalam skala provinsi maupun kabupaten/kota. Tingginya jumlah PDRB suatu daerah menunjukkan semakin besar pula potensi sumber penerimaan daerah tersebut.
Berdasarkan data Badan Pusat Statistik (BPS) pertumbuhan PDRB Provinsi Kalimantan Timur terus mengalami peningkatan secara konsisten di setiap tahunnya. Rata-rata laju pertumbuhan ekonomi sepanjang periode 2006-2017 adalah sebesar 2,88 persen. Kontribusi lapangan usaha terbesar dalam pembentukkan PDRB Provinsi Kalimantan Timur didominasi oleh sektor lapangan usaha berbasis sumber daya alam, seperti lapangan usaha pertambangan sebesar 43,34 persen, lapangan usaha industri sebesar 20,51 persen serta lapangan usahan pertanian, kehutanan dan perikanan sebesar 8,06 persen. Pada tahun 2016 Provinsi Kalimantan Timur memperoleh PDRB Atas Dasar Harga Berlaku (ADHB) sebesar Rp.507.070.000,00 dan PDRB Atas Dasar Harga Konstan (ADHK) sebesar Rp. 438.980.000,00. Besaran nilai PDRB tersebut menempatkan Kalimantan Timur pada posisi keenam sebagai provinsi yang memiliki PDRB tinggi di Indonesia (Produk Domestik Regional Bruto Kabupaten/Kota di Provinsi Kalimantan Timur Menurut Lapangan Usaha 2012-2016, 2017).
Provinsi Kalimantan Timur merupakan penyumbang emisi CO2 terbesar ketiga di Indonesia. Rata-rata emisi CO2 yang dihasilkan Provinsi Kalimantan Timur dari tahun 2007 hingga tahun 2016 yaitu sebesar 7.828.986 ton CO2 per tahun. Hasil analisis data Dinas Lingkungan Hidup (DLH) menyatakan bahwa faktor penyebab utama emisi tersebut adalah pengambilan fungsi lahan hijau menjadi kawasan komersil, seperti lahan perkebunan kelapa sawit, lahan pendukung aktivitas ekonomi terkait kegiatan kehutanan, lahan pertambangan batubara dan industri. Berdasarkan hal tersebut dapat dikatakan bahwa terdapat hubungan negatif antara pertumbuhan ekonomi terhadap kualitas lingkungan (Profil Emisi CO2 Provisi Kalimantan Timur, Dinas Lingkungan Hidup Provinsi Kalimantan Timur, 2015).
Penanggulangan dampak negatif akibat peningkatan emisi CO2 dilakukan oleh Pemerintah Provinsi Kalimantan Timur. Pada tahun 2012 Pemerintah Provinsi Kalimantan Timur telah menyusun dokumen Rencana Aksi Daerah Penurunan Emisi Gas Rumah Kaca (RAD GRK) dan mengeluarkan Peraturan Gubernur Nomor 54 terkait kegiatan penurunan emisi. Kebijakan yang tertuang dalam RAD GRK sifatnya menyeluruh karena mencakup seluruh sektor berbasis lahan, energi dan transportasi. Penyusunan dokumen ini diharapkan dapat memberikan panduan bagi Pemerintah Provinsi dan Pemerintah Kabupaten/Kota dalam upaya penekanan laju emisi setiap sektor ekonomi wilayahnya.
Berdasarkan uraian di atas dapat disimpulkan bahwa terdapat keterkaitan antara emisi yang berasal dari deforestasi dan degradasi hutan terhadap pertumbuhan ekonomi. Penelitian ini bertujuan untuk melihat besarnya pengaruh emisi CO2 terhadap pertum-
buhan ekonomi Provinsi Kalimantan Timur. Hasil dari penelitian ini diharapkan dapat memberi masukan kepada pemerintah dalam hal penyusunan rancangan kegiatan penurunan emisi CO2 karena disertai dengan estimasi dampak panjang pengaruh kebijakan penurunan emisi terhadap pertumbuhan ekonomi Provinsi Kalimantan Timur.
-
2. Metode Penelitian
Data yang digunakan dalam penelitian ini yaitu data dari faktor-faktor emisi (X ), dan PDRB Kabupaten/Kota di provinsi Kalimantan Timur (Y). Data tersebut dianalisis dengan metode analisis komponen utama, analisis regresi linier berganda dan analisis jalur menggunakan bantuan software R.
-
2.1 Analisis Komponen Utama
Analisis komponen utama merupakan suatu teknik yang mereduksi sejumlah data yang banyak (multivariat) dengan mengubah matriks data asli menjadi suatu set kombinasi linier yang lebih sedikit namun dapat menyerap sebagian besar informasi dari data asli (Supranto, 2004). Berikut merupakan bentuk persamaan matriks komponen analisis komponen utama.
Cnx1 = AnxnXnx1 (1)
dengan: C = Matriks kombinasi linier
X = Vektor kolom variabel awal
A = Matriks transformasi variabel awal
Persamaan (1) dapat dinyatakan sebagai berikut.
|
C1 " |
^ a11 |
a12 |
, , a1 n |
^ X1 " | ||
|
C2 |
= |
a21 |
a22 |
" a 2 n |
X2 |
(2) |
|
Cn _ |
_ an 1 |
an2 |
a nn |
_ Xn _ |
Terdapat dua cara yang digunakan dalam analisis komponen utama yaitu dengan menggunakan matriks varian kovarian (matriks ragam peragam) dan matriks korelasi. Setelah ditentukan matriks yang akan digunakan dalam analisis komponen utama, langkah selanjutnya yaitu mencari nilai eigen (λn) dengan λ > λ >■■> λ dari matriks tersebut. Apabila ragam total yang diperoleh sebesar 70 – 80 persen, untuk nyang besar dapat dihubungkan melalui komponen utama pertama, kedua atau ketiga. Komponen utama ini dapat digunakan untuk menggantikan n variabel awal tanpa kehilangan informasi.
(Supranto, 2004)
-
2.2 Analisis Regresi Linier Berganda
Analisis regresi linier berganda adalah hubungan secara linier antara dua atau lebih variabel bebas(X1,X2,∙∙-Xn)terhadap variabel terikat (Yi). Bentuk umum persamaan regresi linier berganda ditunjukkan oleh persamaan berikut.
Yt = βo + βιXt 1 + β2Xt2 + - - - + βkXtk + et (3)
dengan:
Y = Variabel terikat observasi ke-t
-
X, X = Variabel bebas pada observasi observasi ke-t parameter k
β = Parameter intercept
β, β2, ∙ ∙ ∙, βk = Parameter koefisien regresi variabel bebas parameter k
e = Galat/error observasi ke-t
(Rawlings, Pantula, & Dickey, 1998)
-
2.3 Analisis Jalur
Analisis jalur dikenal sebagai model sebab akibat (causing modeling). Pada dasarnya analisis jalur merupakan sebuah teknik pengembangan model regresi yang diuraikan lebih rinci dan menghasilkan beberapa informasi. Informasi yang diperoleh dalam analisis jalur yaitu berupa pengaruh langsung dan tidak langsung antar variabel. Nama variabel yang digunakan dalam analisis jalur adalah variabel eksogen (variabel bebas), variabel intervening (variabel perantara) dan variabel endogen (variabel terikat). Besarnya pengaruh dalam analisis jalur ditunjukkan oleh nilai koefisien jalur pada setiap hubungan kausal antara variabel eksogen (X1) terhadap variabel perantara (Y.) serta dampaknya terhadap variabel endogen
(Z). Berikut merupakan tahapan kerja dalam menghitung koefisien jalur.
-
1. Menentukan struktur hubungan antar variabel.
Langkah pertama dalam analisis jalur yaitu menjelaskan hubungan antar variabel secara diagramatik (diagram jalur). Bentuk diagram jalur ditentukan oleh kerangka pemikiran dan perumusan masalah penelitian.
-
2. Menghitung koefisien korelasi variabel eksogen.
Koefisien korelasi dapat dihitung menggunakan korelasi sederhana sebagai berikut.
r = n ∑ 'XY-Z' Xi ∑ 'Y (4)
n n ∑ n Xi3-(∑ -X. )2 ] n ∑ -Yi2-(∑ ’.Y, )2
-
3. Membentuk matriks korelasi variabel eksogen.
Berikut merupakan matriks korelasi antar variabel eksogen yang digunakan dalam model analisis jalur.
1 r12 r1p
r21 1 r2p
(5)
rp1 rp2 1
-
4. Membentuk matriks invers korelasi variabel eksogen.
Matriks invers korelasi antar variabel eksogen yang digunakan dalam model
analisis jalur ditunjukkan oleh persamaan sebagai berikut.
X1X2Xk
R-1
X1 CR11 CR12
CR1k
(6)
Xk CRkl CRk2 ■■■ CRkk
k k 1k 2 kk
-
5. Membentuk matriks korelasi variabel eksogen terhadap variabel endogen.
Selain matriks korelasi antar masing-masing variabel eksogen, dibentuk pula matriks yang berisi koefisien korelasi variabel eksogen terhadap variabel endogen. Berikut merupakan matriks koefisien korelasi antar variabel eksogen dan variabel endo-
gen.
Y
RYX1 =
X1
rXY
(7)
Xk L rXY
-
6. Menghitung koefisien jalur.
Nilai koefisien jalur dapat diperoleh dengan cara mengalikan matriks invers korelasi antar variabel eksogen dan matriks korelasi antar variabel eksogen terhadap variabel endogen.
CR1
: = :
rYXk J LCRki
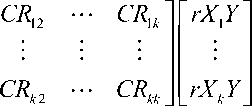
(8)
dengan:
ρYXi = Matriks koefisien jalur variabel eksogen dan variabel endogen
R 1 = Invers matriks koefisien korelasi antar variabel eksogen
R = Matriks korelasi antar variabel eksogen dan variabel endogen
-
7. Menghitung besarnya pengaruh.
Pengaruh dalam analisis jalur dibagi menjadi 2 jenis, yaitu pengaruh langsung dan pengaruh tidak langsung. Berikut merupakan cara menghitung masing-masing pengaruh tersebut.
-
a. Pengaruh langsung
Xi → Y = ρYXi (9)
-
b. Pengaruh tidak langsung
Xi → Y → Z = ρYXlρYZ (10)
(Dillon, W.R, Goldstein, 1984) 3. Hasil dan Pembahasan
Berikut merupakan hasil analisis data dari masing-masing tahapan penelitian. Tahapan penelitian dimulai dari analisis komponen utama, analisis regresi dan analisis jalur.
-
3.1 Analisis Komponen Utama
∑ Y=
0,617
0,788
0,252
0,777
0,617
0,675
0,785
0,493
0,501
0,788
1,012
0,318
0,992
0,786
0,864
1,005
0,632
0,642
0,252
0,318
0,109
0,319
0,256
0,276
0,319
0,200
0,203
0,777
0,992
0,319
0,981
0,781
0,852
0,991
0,622
0,632
0,617
0,786
0,256
0,781
0,624
0,677
0,788
0,494
0,501
0,675
0,864
0,276
0,852
0,677
0,741
0,861
0,541
0,549
0,785
1,005
0,319
0,991
0,788
0,861
1,003
0,629
0,639
0,493
0,632
0,200
0,622
0,494
0,541
0,629
0,395
0,402
0,501
0,642
0,203
0,632
0,501
0,549
0,639
0,402
0,408
Analisis komponen utama dalam penelitian ini menggunakan matriks varian kovarian. Bentuk matriks varian kovarian dari faktor-faktor emisi (Xi) dan PDRB Kabupaten/Kota (Yi) sebagai berikut.
|
∑ X = |
"2,051378 0,159027 0,008094 0,296209 ’ 0,159027 0,058179 0,001112 0,017461 0,008094 0,001112 0,000194 -0,004614 _0,296209 0,017461 -0,004614 0,545766 _ |
Berdasarkan matriks varian dan kovarian data, diperoleh persamaan kombinasi linier yang terbentuk dari vektor eigen masing-masing matriks.
S1 = 0,97967X1 + 0,07713X2 + 0,00338X3 + 0,18519X4
S2 = 0,18349X1 + 0,02788X2 + 0,01236X3 - 0,98255X4
T = -0,32384^ - 0,41426X2 - 0,1324373 - 0,40856X4 - 0,32484K5
-0,35510ζ -0,41318K7 -0,25943⅞ -0,26347⅞
Selanjutnya, tabel proporsi dan proporsi kumulatif dari kombinasi linier yang diperoleh ditunjukkan oleh Tabel 1 dan Tabel 2.
Tabel 1. Proporsi Kumulatif Faktor-Faktor Emisi CO2
|
Kombinasi Linier |
Nila Eigen |
Proporsi |
Proporsi Kumulatif |
Persentase Kumulatif |
|
1 |
2,119921 |
0,7983 |
0,7983 |
79,83 % |
|
2 |
0,4900091 |
0,1845 |
0,9828 |
98,28 % |
|
3 |
0,04549612 |
0,01713 |
0,99997 |
99,997 % |
|
4 |
0,000092 |
0,000030 |
1 |
100 % |
|
Tabel 2. Proporsi Kumulatif PDRB Kabupaten/Kota | ||||
|
Kombinasi Linier |
Nilai Eigen |
Proporsi |
Proporsi Kumulatif |
Persentase Kumulatif |
|
1 |
5,872362 |
0,997 |
0,997 |
99,7 % |
|
2 |
l,377652e^02 |
0,00234 |
0,99933 |
99,93 % |
|
3 |
2,478398e^03 |
0,00042 |
0,99975 |
99,97 % |
|
4 |
7,005460e-°4 |
0,00012 |
0,99987 |
99,98 % |
|
5 |
4,109531e^°* |
0,00007 |
0,99994 |
99,99 % |
|
6 |
2,463937e^04 |
0,00004 |
0,99998 |
99,99 % |
|
7 |
5,827180e^05 |
0,000010 |
0,999990 |
99,99 % |
|
8 |
3,178497e^05 |
0,000010 |
1 |
100 % |
|
9 |
l,872758e^05 |
0,000000 |
1 |
100 % |
Berdasarkan tabel nilai proporsi kumulatif yang disajikan dalam Tabel 1 dan Tabel 2, diperoleh variabel baru sebagai hasil analisis komponen utama terhadap faktor-faktor emisi CO2 dan jumlah PDRB Kabupaten/Kota yaitu variable S , S dan T karena cukup untuk menjelaskan keragaman data awal dengan proporsi kumulatif sebesar 98,28 persen dan 99,7 persen. Variabel baru tersebut yang digunakan dalam mengesti-masi pengaruh dari emisi CO2 terhadap jumlah PDRB menggunakan analisis regresi dan analisis jalur model trimming.
-
3.2 Diagram Jalur
Diagram jalur merupakan alat untuk menggambarkan secara grafis struktur hubungan kausalitas antar variabel eksogen, variabel perantara dan variabel endogen. Bentuk diagram jalur penelitian sebagai berikut.

Gambar 1. Diagram Jalur Penelitian
-
3.3 Analisis Regresi
Persamaan substruktur pertama menggambarkan pengaruh dari S dan S terhadap T . Berdasarkan hasil pengujian asumsi klasik, substruktur pertama memerlukan variabel bebas T untuk menghilangkan masalah autokorelasi pada model awal, sehingga estimasi pada substruktur pertama dilakukan dengan S dan S dan T terhadap T . Hasil dari estimasi tersebut ditunjukkan oleh Tabel 3.
Tabel 3. Hasil Analisis Regresi Substruktur Pertama
|
Model Regresi |
Variabel Bebas |
Varibel Terikat |
Coefficients |
P-value |
R-Square |
|
Intercept |
- 0,2357 |
0,44338 | |||
|
1 |
S1 |
Tt |
0,7136 |
0,01400 |
0,9361 |
|
S2 |
0,7616 |
0,17444 | |||
|
Tt-1 |
0,6843 |
0,00276 |
Tabel 3 menunjukkan nilai p-value untuk variabel bebas S lebih dari α = 0,05 . Oleh karena itu dilakukan estimasi kedua dengan mengeluarkan variabel S dalam model regresi. Hasil estimasi kedua ditunjukkan oleh Tabel 4.
Tabel 4. Hasil Analisis Regresi Kedua Substruktur Pertama
Model Regresi Var a e Varibel Terikat Coefficients P-value R-
Bebas Square
|
Model Regresi |
Variabel Bebas |
Varibel Terikat |
Coefficients |
P-value |
R-Square |
|
Intercept |
- 0,4065 |
0,21461 | |||
|
1 |
S1 |
Tt |
0,7014 |
0,01736 |
0,9041 |
|
T-1 |
0,7186 |
0,00197 |
Berdasarkan hasil estimasi pada Tabel 4. diperoleh nilai p-value seluruh variabel bebas telah kurang dari α = 0,05, sehingga persamaan regresi untuk substruktur pertama adalah sebagai berikut.
T =-0,4065 + 0,7014S1 + 0,7186T 1
Substruktur kedua menggambarkan pengaruh antara variabel S , S dan T terhadap Z . Hasil estimasi yang diperoleh dari model substruktur kedua ditunjukkan oleh tabel berikut.
Tabel 5. Hasil Analisis Regresi Substruktur Kedua
|
Model Regresi |
Variabel Varibel Terikat Coefficients P-value R-Square |
|
2 |
Intercept 274,225 1,61e-09 S1 9,462 0,0121 S2 Zt 8,805 0,1353 0,9989 T 67,471 1,49e-07 |
Berdasarkan hasil Tabel 5, analisis regresi kembali dilakukan dengan mengeluarkan variabel S dalam model regresi karena pada hasil estimasi pertama nilai p-value variabel ini lebih dari α = 0, 05 . Hasil estimasi kedua model substruktur kedua disajikan dalam tabel berikut.
Tabel 6. Hasil Analisis Regresi Kedua Substruktur Kedua
|
Model Regresi |
Variabel Bebas |
Varibel Terikat |
Coefficients |
P-value |
R-Square |
|
Intercept |
272,507 |
9,87e-11 | |||
|
2 |
S1 |
Zt |
8,283 |
0,0143 |
0,9982 |
|
Tt |
68,619 |
1,72e-08 |
Berdasarkan hasil estimasi pada Tabel 6, seluruh nilai p-value hasil variabel bebas telah menujukkan nilai kurang dari α = 0,05 . Selanjutnya, hasil tersebut dibentuk menjadi persamaan regresi di bawah ini.
Zt = 272,570 + 8,283S1 + 68,619T
Hubungan kausal antar variabel pada substruktur pertama terbentuk dari S dan S terhadap T . Berikut ini merupakan bentuk diagram jalur substruktur pertama.
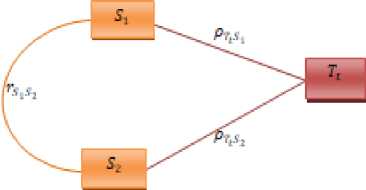
Gambar 2. Hubungan Kausal Substruktur Pertama
Diagram jalur substruktur pertama mengalami perubahan sebagai berikut.

Gambar 3. Hubungan Kausal Substruktur Pertama Model Trimming
Selanjutnya, dilakukan perhitungan koefisien jalur terhadap model substruktur pertama. Langkah pertama dalam analisis jalur yaitu membuat matriks korelasi antara variabel eksogen S dan T menggunakan Persamaan (5).
T
S1 1 0,3475665
Tt_, ⅛3475665 1
Berikut merupakan bentuk invers matriks korelasi yang diperoleh dari Persamaan (6).
R
,-1
S1
Tt-1
Si Tt-1
1,1374008 -0,3953224
-0,3953224 1,1374008
Setelah itu, dilakukan pembentukan matriks korelasi antara variabel S dan T terhadap T seperti yang ditunjukkan pada Persamaan (7).
Tt
RST
S1
T-1
0,6838268
0,8571276
Persamaan (8) digunakan dalam menghitung nilai koefisien jalur. Nilai tersebut diperoleh dari operasi perkalian matriks R 1 dengan matriks Rsτ .
Pts _ 1,1374008 -0,3953224
P,τ,l = [-0,3953224 1,1374008
_ -0,6838268∏Γ0,4389434^
" 0,8571276 0,7045655
Berdasarkan hasil perhitungan koefisien jalur diagram jalur pertama, diperoleh nilai koefisien jalur untuk S sebesar 0, 4389434 dan T sebesar 0,7045655. Hasil ini disajikan pada Tabel 7 dan telah sesuai dengan perhitungan koefisien jalur menggunakan bantuan software R.
Tabel 7. Hasil Perhitungan Koefisien Jalur Substruktur Pertama
Variabel Koefisien Jalur
S 0,4389434
T 0,7045655
Berikut merupakan bentuk diagram jalur substruktur pertama yang disertai dengan nilai koefisien jalurnya.

Gambar 4. Diagram Jalur Substruktur Pertama Model Trimming
Perhitungan terus dilanjutkan pada substruktur kedua, sehingga diperoleh hasil perhitungan koefisien jalur untuk substruktur kedua sebagai berikut.
Tabel 8. Hasil Perhitungan Koefisien Jalur Substruktur Kedua
|
Variabel |
Koefisien Jalur |
|
S1 |
0,07166816 |
|
Tt |
0,94870721 |
Berdasarkan hasil pada Tabel 7 dan Tabel 8, diperoleh bentuk diagram jalur penelitian yang disertai koefisien jalur masing-masing variabelnya. Diagram jalur tersebut ditunjukkan oleh gambar berikut.

Gambar 5. Hubungan Kausal Variabel S , T dan T Terhadap Z
Pada analisis jalur diperhitungkan seluruh pengaruh dari variabel eksogen terhadap variabel endogen baik secara langsung maupun tidak langsung. Rincian besarnya masing-masing pengaruh langsung dan tidak langsung disajikan oleh tabel berikut.
Tabel 9. Pengaruh Langsung dan Pengaruh Tidak Langsung Diagram Jalur Penelitian
|
Pengaruh Variabel |
Pengaruh | |||
|
Langsung |
Tidak Langsung (Melalui T |
Total | ||
|
S1 |
Tt |
0, 4389 |
— |
0, 4389 |
|
S1 |
Zt |
0,0717 |
0, 4164 |
0,4881 |
|
Tt-1 |
→Tt |
0,7046 |
- |
0,7046 |
|
Tt-1 |
Zt |
- |
0,6684 |
0,6684 |
|
Tt |
Zt |
0,9487 |
- |
0,9487 |
3.5 Proyeksi PDRB Provinsi Kalimantan Timur
Hasil analisis regresi dan analisis jalur menyatakan bahwa tingkat emisi karbondioksida (CO2) memiliki pengaruh terhadap jumlah PDRB Kabupaten/Kota maupun PDRB Provinsi Kalimantan Timur. Hal tersebut dapat terjadi karena sebagian besar jumlah Produk Domestik Regional Bruto (PDRB) Provinsi Kalimantan Timur ditunjang oleh sektor ekonomi berbasis lahan. Oleh karena itu, apabila komitmen pemerintah dalam menurunkan emisi CO2 dilaksanakan dan mencapai target yang telah ditentukan,
maka akan berpotensi memberi dampak lain terhadap tingkat pertumbuhan ekonomi. Dampak tersebut dapat dilihat dari hasil proyeksi jumlah PDRB selama beberapa tahun kedepan. Hasil proyeksi PDRB Provinsi Kalimantan Timur dapat dilihat pada Tabel 10.
Tabel 10. Proyeksi Nilai PDRB Provinsi Kalimantan Timur (Miliar Rupiah)
|
Tahun |
Proyeksi Nilai PDRB |
|
2017 2018 2019 2020 2021 2022 2023 2024 2025 2026 2027 2028 2029 |
455.628.000.000 455.122.000.000 445.706.000.000 454.603.000.000 452.316.000.000 449.208.000.000 445.537.000.000 441.489.000.000 437.198.000.000 432.757.000.000 428.236.000.000 423.681.000.000 419.128.000.000 |
|
2030 |
414.600.000.000 |
Skenario penurunan emisi CO2 dilakukan pada penelitian ini untuk melihat fluktuasi jumlah PDRB Provinsi Kalimantan Timur apabila laju penurunan emisi mengalami peningkatan sebesar 3 persen dan 5 persen. Hasil proyeksi nilai PDRB akibat skenario tersebut ditunjukkan oleh tabel berikut.
Tabel 11. Skenario Proyeksi Nilai PDRB Provinsi Kalimantan Timur (Miliar Rupiah)
|
Tahun |
Proyeksi Nilai PDRB | |
|
Penurunan emisi CO2 3 Persen |
Penurunan emisi CO2 5 Persen | |
|
2017 |
401.114.000.000 |
399.218.000.000 |
|
2018 |
402.466.000.000 |
397.664.000.000 |
|
2019 |
401.053.000.000 |
392.744.000.000 |
|
2020 |
397.724.000.000 |
385.597.000.000 |
|
2021 |
393.088.000.000 |
377.029.000.000 |
|
2022 |
387.581.000.000 |
367.612.000.000 |
|
2023 |
381.512.000.000 |
357.748.000.000 |
|
2024 |
375.103.000.000 |
347.717.000.000 |
|
2025 |
368.511.000.000 |
337.714.000.000 |
Proyeksi Nilai PDRB
Tahun Penurunan emisi CO2 Penurunan emisi CO2
3 Persen 5 Persen
|
2026 |
361.848.000.000 |
327.870.000.000 |
|
2027 |
355.190.000.000 |
318.274.000.000 |
|
2028 |
348.594.000.000 |
308.982.000.000 |
|
2029 |
342.095.000.000 |
300.028.000.000 |
|
2030 |
353.719.000.000 |
291.431.000.000 |
Berdasarkan hasil penelitian (Empora & Mamunneas, 2011), dibuktikan bahwa tingkat emisi mempengaruhi pertumbuhan ekonomi suatu wilayah, sehingga pertumbuhan ekonomi akan bergantung kepada tingkat emisi yang dicapai dalam jangka waktu tertentu. Hal tersebut juga telah sesuai dengan hasil penelitian ini yaitu terdapat pengaruh emisi terhadap pertumbuhan ekonomi di Provinsi Kalimantan Timur. Kebijakan penurunan emisi CO2 menimbulkan dampak seperti menurunannya PDRB Provinsi Kalimantan Timur seperti yang ditunjukkan pada Tabel 10. dan Tabel 11. Berdasarkan hasil tersebut bahwa semakin besar nilai penurunan emisi CO2 akan mengakibatkan proyeksi nilai PDRB yang turun secara signifikan, sehingga target tercapainya pembangunan ekonomi dan penurunan emisi CO2 tidak dapat tercapai secara bersamaan. Apabila pemerintah menjadikan penurunan emisi CO2 sebagai prioritas dalam pembangunan daerah maka target penurunan emisi akan tercapai, namun disisi lain akan menimbulkan keterlambatan pertumbuhan ekonomi. Dampak lain pengaruh emisi terhadap pertumbuhan ekonomi juga disebutkan dalam penelitian yang dilakukan oleh (Nababan, 2015) bahwa kebijakan penurunan emisi akan menimbulkan penurunan kinerja ekonomi serta pergeseran struktur ekonomi Provinsi Kalimantan Timur. Penurunan kinerja dan pergeseran struktur ekonomi tersebut pada akhirnya akan membawa dampak lainnya, seperti penurunan penyerapan tenaga kerja.
-
4. Kesimpulan dan Saran
Berdasarkan hasil dan pembahasan yang telah dilakukan, maka dapat ditarik beberapa kesimpulan sebagai berikut.
-
1. Pertumbuhan ekonomi Provinsi Kalimantan Timur dipengaruhi oleh tingkat emisi karbondioksida (CO2).
-
2. Estimasi dampak jangka panjang kebijakan penurunan emisi karbondioksida (CO2) terhadap pertumbuhan ekonomi dapat dilihat dari hasil proyeksi jumlah nilai Produk Domestik Regional Bruto (PDRB) Atas Dasar Harga Berlaku Menurut Lapangan Usaha Provinsi Kalimantan Timur. Berdasarkan hasil proyeksi tersebut apabila kebijakan penurunan emisi diterapkan dan mencapai target yang telah ditentukan yaitu sebesar 1,097 persen maka akan mengakibatkan penurunan terhadap jumlah PDRB Provinsi Kalimantan Timur sebesar 2,92 persen. Semakin besar ketetapan penurunan emisi akan menurunkan jumlah PDRB secara signifikan.
-
3. Pada penelitian selanjutnya yang terkait dengan estimasi pengaruh kebijakan penurunan emisi CO2 terhadap pertumbuhan ekonomi adalah mempertimbangkan penambahan pengaruh variabel lain dan menggunakan metode analisis regresi lainnya, semisal dengan pendekatan Bayesian.
Daftar Pustaka
Dillon, W.R, Goldstein, M. (1984). Multivariate Analysis Method and Application. New York: Willey & Sons Inc.
Empora, N., & Mamunneas, T. P. (2011). The Effect of Emmisions on US State Total Factor Productivity Growth. Review of Economic Analysis, 3, 149–172.
Nababan, Y. J. (2015). Inclusive Green Economy Di Provinsi Kalimantan Timur: Trade-Off Antara Pen-gurangan Emisi dan Kinerja Ekonomi. Institut Pertanian Bogor.
Produk Domestik Regional Bruto Kabupaten/Kota di Provinsi Kalimantan Timur Menurut Lapangan Usaha 2012-2016. (2017). Samarinda.
Profil Emisi CO2 Provisi Kalimantan Timur, Dinas Lingkungan Hidup Provinsi Kalimantan Timur. (2015). Samarinda.
Rawlings, J. O., Pantula, S. G., & Dickey, D. A. (1998). Applied Regression Analysis A Research Tool 2nd Edition (2nd ed.). New York: Springer-Verlag.
Supranto. (2004). Analisis Multivariat: Arti dan Interpretasi. Jakarta: Adi Mahastya.
49
Discussion and feedback