Model Deret Waktu Produksi Genteng Pejaten dalam Keterbatasan Sumber Daya
on
Jurnal Matematika Vol. 8 No.2, Desember 2018, pp.126-138
Article DOI: 10.24843/JMAT.2018.v08.i02.p105
ISSN: 1693-1394
Model Deret Waktu Produksi Genteng Pejaten dalam Keterbatasan Sumber Daya
I Gusti Ayu Made Srinadi
Program Studi Matematika, FMIPA, Universitas Udayana
Email: srinadi@unud.ac.id
Desak Putu Eka Nilakusmawati
Program Studi Matematika, FMIPA, Universitas Udayana
Email: nilakusmawati@unud.ac.id
Abstract : The sample of this research was taken by purposive sampling technique, the villagers of Pejaten who are tile craftsmen. Data was collected through a questionnaire filled with 105 tile craftsmen. The tile materials of Pejaten Village include clay and rocky soil, clay is currently almost 95% from outside the village of Pejaten. The clay supplier villages include Bantas Village, Selemadeg, Meliling, Jadi, Gadungan, and Pandak. Most of the coconut fiber fuel is mostly imported from Jembrana Regency. Some laborers in tile production are family members of craftsmen and most use wage labor. This condition shows the scarcity of tile production resources in Pejaten Village. This study aims to find out how tile production in Pejaten village is in a condition of limited resources, and how the forecasting model of tile production is based on historical data from January 2013 to December 2017. The results of in-depth interviews with several tile craftsmen state that they will continue to produce tile along the roof tile demand still exists and is able to provide raw materials even though most are imported from outside the Pejaten Village. The amount of tile production shows a seasonal trend, and the time series model that is most suitable for the number of tile production is the SARIMA (1,1,5) (1,1,1) 12 model.
Keywords: tile craftsmen, tile materials, coconut fiber fuel, seasonal trend, SARIMA
Desa Pejaten terletak di wilayah Kecamatan Kediri, Kabupaten Tabanan merupakan daerah yang tidak memiliki areal persawahan (subak). Warga Desa Pejaten yang memiliki sawah terletak di sekitar wilayah Desa Pejaten, diantaranya Subak Nyitdah, Subak Beda, dan Subak Bengkel. Mata pencaharian sebagian besar penduduk Desa Pejaten adalah sebagai pengrajin genteng. Hingga saat ini 80% atau sekitar 800 Kepala Keluarga (KK) masih bergelut dengan usaha genteng. Desa Pejaten dikenal sebagai sentra industri cetakan berbahan baku tanah, terlengkap dan terbesar di Bali seperti genteng, gerabah, bata, dan keramik (Nurbawa, 2017). Sebagian besar warga Bali, meskipun banyak orang tidak tahu di mana letak Desa Pejaten, namun akan mengingat nama Pejaten jika melihat genteng. Genteng produksi Desa Pejaten ikut andil dalam pembangunan rumah, kantor, warung atau bangunan lain, bukan hanya di sekitar Tabanan, melainkan di seluruh daerah Bali, bahkan menyebar hingga Lombok dan Banyuwangi.
Keterbatasan tanah liat di Desa Pejaten mengakibatkan tanah liat sebagai bahan baku genteng mulai didatangkan dari luar wilayah Pejaten sejak tahun 1996, diantaranya dari Desa Bantas Selemadeg, Meliling, Jadi, dan Pandak. Sebagian pengrajin melibatkan
anggota keluarga sebagai tenaga kerja, sebagian besar menggunakan tenaga upah yang berasal dari Lombok dan Jawa. Bahan bakar yang digunakan untuk membakar genteng kering hampir semuanya menggunakan kayu bakar atau serabut kelapa yang didatangkan dari Kabupaten Jembrana.
Walaupun beberapa pengrajin merasa bahan baku tanah di Desa Pejaten sangat terbatas, kerajinan genteng tetap eksis sampai saat ini. Hal ini dikarenakan mata pencaharian ini dapat diandalkan dan permintaan genteng masih terus ada. Sekitar 800 kepala keluarga (KK) memanfaatkan kerajinan genteng sebagai sumber pendapatan keluarga, baik sebagai sumber pendapatan utama ataupun sampingan. Di samping bahan tanah didatangkan dari luar wilayah Desa Pejaten, beberapa pengrajin genteng juga kekurangan tenaga kerja, karena banyak tenaga upah saat ini lebih tertarik bekerja ke luar negeri tergiur oleh gaji yang lebih besar. Kekurangan tenaga buruh mengakibatkan banyak pengrajin hanya mengandalkan tenaga dari anggota keluarganya sendiri sehingga jumlah produksi genteng menurun. Pengrajin banyak menolak pesanan dalam jumlah besar karena takut tidak dapat melayani, dan hanya menerima pesanan dalam jumlah kecil atau pesanan perorangan.
Data jumlah produksi pengrajin genteng dan informasi bahwa jumlah genteng yang dihasilkan seluruhnya habis terjual memberikan informasi mengenai jumlah permintaan genteng. Informasi mengenai jumlah permintaan genteng masa-masa terdahulu dapat digunakan untuk meramalkan jumlah permintaan genteng pada masa yang akan datang. Karena data yang terekam adalah data jumlah produksi genteng, maka penelitian ini bertujuan untuk menentukan model peramalan produksi genteng di Desa Pejaten berdasarkan data histori Januari 2013 hingga Desember 2017, berupa data produksi bulanan. Diketahuinya pola produksi atau pola permintaan genteng, dapat digunakan oleh pengrajin untuk antisipasi dalam mempersiapkan produksi genteng sehingga mampu melayani permintaan konsumen.
Teknik sampling untuk pengumpulan data melalui kuisioner mengenai ketersediaan sumber daya dengan pemilihan banjar/dusun serta KK pengrajin genteng. Dari sumber data informasi desa dilakukakan tabulasi data jumlah produksi genteng atau jumlah pesanan genteng. Data yang sudah ditabulasi dianalisis secara deskriptif untuk mengetahui karakteristik pengrajin, kondisi sumber daya produksi yang dihadapi pengrajin, model rataan produksi menurut sumber daya, dan membentuk model time series produksi genteng dalam sepuluh tahun terakhir dari 2013 sampai dengan 2017.
Dalam tahapan pengumpulan data ditetapkan variabel-variabel penelitian yang diamati, mencakup skala pengukuran variabel, instrumen penelitian, dan lokasi pengambilan data. Data penelitian merupakan data primer yang dikumpulkan melalui kuisioner terhadap 120 Kepala Keluarga (KK) yang merupakan pengrajin genteng di Desa Pejaten, namun hanya 105 kuisioner yang terisi lengkap dan dapat dianalisis untuk menjawab tujuan penelitian.
Kondisi keterbatasan sumber daya produksi genteng diperlihatkan secara deskriptif dari variabel-variabel penelitian yang mencakup sumber daya produksi
genteng meliputi: 1) bahan baku (tanah merah/tanah liat), 2) tanah cadas (campuran tanah liat), 3) bahan bakar (serabut kelapa), 4) tenaga kerja, dan jumlah produksi genteng. Sumber daya seperti bahan baku (tanah merah/tanah liat) dapat dibedakan dari sumber perolehannya apakah dari tanah milik sendiri yang dicangkul dan diolah menjadi tanah liat atau dengan membeli tanah cangkul dalam truk selanjutnya diolah menjadi tanah liat, atau langsung membeli tanah liat yang sudah siap dicetak menjadi genteng. Demikian juga untuk tenaga kerja, apakah menggunakan tenaga kerja dari anggota keluarga sendiri atau juga menggunakan tenaga kerja upah/buruh. Semua informasi yang ditetapkan sebagai variabel penelitian diuraikan dalam pernyataan ataupun pertanyaan yang disusun dalam kuisioner.
Untuk menentukan model peramalan jumlah produksi genteng, digunakan analisis data deret waktu. Kegiatan meramal adalah memperkirakan kejadian pada masa yang akan datang, sedang membuat prediksi atau ramalan disebut dengan peramalan (Bowerman et al, 2005). Peramalan umumnya memiliki asumsi pola masa lampau berlanjut ke masa depan. Klasifikasi peramalan menurut Abraham dan Ledolter (2005) dibedakan menjadi dua yaitu peramalan kualitatif dan peramalan kuantitatif. Peramalan kualitatif merupakan peramalan yang umumnya hanya berdasarkan intuisi, metode peramalannya tidak dapat direproduksi oleh orang lain karena penyusunnya tidak menguraikan secara eksplisit bagaimana informasi yang tersedia dimasukkan dalam peramalan. Peramalan kuantitatif merupakan peramalan yang didasarkan pada data masa lalu, menggunakan model matematika atau statistika untuk meramalkan masa depan. Pada penelitian ini menggunakan peramalan kuantitatif.
Kegunaan peramalan terlihat pada saat pengambilan keputusan atau menetapkan kebijakan. Keputusan yang baik didasarkan atas pertimbangan apa yang akan terjadi saat keputusan itu dilaksanakan. Peramalan sangat penting untuk perencanaan dan pengendalian operasi dalam berbagai bidang, seperti manajemen produksi, perencanaan keuangan, sistem persediaan kontrol kualitas, dan analisis inverstasi (Wei, 2006).
Data Deret Waktu adalah barisan observasi yang diambil secara berurutan dalam kurun waktu tertentu, baik yang bersifat diskret atau kontinu. Dalam analisis deret waktu, data harus bersifat stasioner. Konsep stasioneritas menurut Makridakis et al (1999) meliputi: 1)jika deret waktu diplotkan, tidak terdapat perubahan nilai mean dari waktu ke waktu, dapat dikatakan deret waktu tersebut stasioner dalam mean. 2)jika deret waktu diplotkan, tidak terdapat perubahan nilai varians dari waktu ke waktu, dapat dikatakan deret waktu tersebut stasioner dalam varians. Suatu deret waktu tidak stasioner dalam mean, dapat distasionerkan dengan melakukan differencing. Differencing adalah pengurangan data tertentu dengan data sebelumnya. Jika differencing orde pertama tidak menghasilkan data yang stasioner, maka dilanjutkan differencing orde kedua, demikian seterusnya hingga diperoleh data stasioner.
Notasi yang sangat bermanfaat dalam metode differencing (Makridakis et al., 1999) adalah operator pergeseran mundur (backward shift) yang disimolkan dengan B, dapat ditulis sebagai:
BXt = Xt - 1 (2.1)
Bila dikembangkan maka B(BX^)=B2Xt =
Differencing untuk orde pertama dapat dinyatakan dalam persamaan (2.2).
∇Xt = - Xt-I (2.2)
= - BXt
=(1-B) Xt
Nilai (1-B) pada (2.2) menyatakan differencing orde pertama. Setelah dilakukan differencing orde pertama namun data masih belum stasioner dalam mean, maka dilakukan lagi differencing orde kedua, demikian seterusnya. Secara umum differencing orde ke-d untuk mencapai stasioner dinotasikan sebagai:
∇ dχt=(1-B) dχt ;d≥1 (2.3)
Data yang belum stasioner dalam varians dapat distasionerkan melalui proses transformasi (Wei, 2006). Persamaan transformasi pangkat (power transformation) dinyatakan dalam persamaan (2.4).
Y(λ)
T(xt)=½ (2.4)
Nilaiλ yang digunakan dalam transformasi pangkat diuraikan dalam Tabel 1.
Tabel 1. Transformasi Box – Cox
|
No |
Nilai λ |
Proses Transformasi |
|
1 |
-1 |
1 |
|
Xt | ||
|
2 |
-0,5 |
1 |
|
√ | ||
|
3 |
0 |
InXt |
|
4 |
0,5 |
√ |
|
5 |
1 |
(tanpa transformasi) |
Sumber: Wei (2006)
Untuk mengetahui apakah data telah stasioner atau tidak, dilakukan Augmented Dickey-Fuller (ADF) test, merupakan perluasan dari Dickey-Fuller test. Untuk model Autoregressive AR(p), bentuk umum persamaan Dickey-Fuller yaitu:
∇Xt = + ΨpXt-l + Th ∇Xt-2+⋯+Vp ∇Xt-p + at
∇Xt = + ΨpXt-l +∑1=2 Vi∇Xt-i+ι + at (2.5)
dengan Φp =∑ ^=1Φi+1 danPi =-∑j=1Φj
Bila persamaan (2.5) ditambahkan dengan komponen trend waktu, maka diperoleh persamaan (2.6)
(2.6)
∇Xt = + Pt +ΨpXt-l +∑f=2 r∣ ∗∇Xt-i+ι + ^t
dengan rl∗=-∑^=i+ι Φj dan (t – 1) adalah panjang lag. Model (2.6) ini yang diuji dengan ADF test. Tiga bentuk model yang diuji dengan ADF test, yaitu
-
1. Model dengan konstanta (µ) dan tren (β) seperti persamaan (2.5)
-
2. Model dengan konstanta (µ),∇X t= +ΦpXt-l +∑f=2 r∣ ∗∇Xt-i+ι + at
-
3. Model tanpa konstanta (µ) dan tren (β), ∇ = +∑f=2 P ∗∇Xt-i+ι + at
Hipotesis yang diuji adalah :
H0 : ψ = 0 (data tidak stasioner) vs H1 : ψ< 0 (data stasioner)
Statistika uji dalam ADF test adalah
t =∑Liφt→ hit = (∑LιΦi)
(2.7)
Keputusan yang diambil adalah tolah H0 atau data stasioner apabila nilai mutlak | ^hit | lebih besar dari nilai t-tabel atau p-value lebih kecil dari taraf nyata α yang ditetapkan, misal α=0,05.
Uji Korelasi Deret Waktu
Korelasi antar deret waktu dengan lag k dapat diukur melalui autokorelasi ( Pk ) (Abraham & Ledolter, 2005) dan (Box et al.,2016). Autokovarians pada lag k dapat dituliskan sebagai:
Yk = (xt , Xt+k)=E(Xt -P)(Xt+k -μ) ;k=0,1,2,…(2.8)
Mengasumsikan data telah stasioner, autokorelasi pada lag k dapat dituliskan sebagai:
Pk = ( t= , Xt ⅛ )=n; k=0,1,2,…(2.9)
√ Var (Xt ) Var (Xt+k) ; ,,,….
Korelasi dalam deret waktu menyatakan hubungan antara Xt dan Xt+k setelah ketergantungan linear dengan Xt+t, Xt+2, …, Xt+k-1dihilangkan. Untuk menghitung korelasi antara Xt dan Xt+k dapat digunakan autokorelasi parsial yang dinyatakan sebagai:
= [(χt- ̂ t- ),(xt+k- ̂t+k)]
=√Var (xt- ̂J) Var (Xt+k ) (2.10)
dengan Xt+k adalah data deret waktu dan t+k adalah nilai dugaan dari Xt+k .
Proses White Noise
Deret waktu dikatakan white noise apabila autokorelasi antara Xt dan Xt+k untuk semua lag k mendekati nol, berarti nilai antar lag pada deret tersebut tidak berkorelasi satu sama lain. Suatu proses {αt}dikatakan white noise apabila{αt}merupakan barisan variabel cak yang tidak berkorelasi dengan nilai tengah konstan E (at) = μa, biasanya diasumsikan bernilai nol dengan varians Var(at) = σ∩ dan γk = Cov( at, at+fc) = 0 untuk setiap fc ≠ 0, serta nilai ACF dan PACF sama dengan nol (Wei, 2006).
Model Deret Waktu Stasioner dan Tidak Stasioner
Model deret waktu secara umum dibedakan menjadi dua, yaitu model deret waktu stasioner dan mode deret waktu tidak stasioner. Model deret waktu stasioner meliputi model autoregressive (AR), model moving average (MA),dan model autoregressive moving average (ARMA). Model deret waktu tidak stasioner meliputi model autoregressive integrated moving average (ARIMA) dan model seasonal autoregressive integrated moving average (SARIMA).
Data penelitian diperoleh melalui kuisioner yang diisi oleh105 Kepala Keluarga (KK) pengerajin genteng di Desa Pejaten.Tabulasi data memberikan informasi mengenai ketersediaan sumber daya produksi, kemudahan akses memperoleh sumber daya produksi diuraikan dalam Tabel 2 – Tabel 5.
Tabel 2. Jumlah Pengrajin Genteng Menurut Cara Peroleh Tanah
|
Frequency |
Percent |
Valid Percent |
Cumulative Percent | ||
|
Valid |
Beli tanah olah sendiri |
105 |
100.0 |
100.0 |
100.0 |
Tabel 3. Jumlah Pengrajin Genteng Menurut Lama_Supply Tanah
|
Frequency |
Percent |
Valid Percent |
Cumulative Percent | |
|
Valid 1.00 |
1 |
1.0 |
1.0 |
1.0 |
|
2.00 |
36 |
34.3 |
34.3 |
35.2 |
|
3.00 |
59 |
56.2 |
56.2 |
91.4 |
|
4.00 |
9 |
8.6 |
8.6 |
100.0 |
|
Total |
105 |
100.0 |
100.0 |
Informasi dari Tabel 2 menggambarkan semua pengrajin memperoleh tanah dengan membeli tanah cangkul per truk, kemudian diolah menjadi tanah liat yang siap dicetak. Menurut pendapat para pengrajin genteng mengenai berapa lama supply tanah tersedia, sebagian besar menyatakan bahwa supply tanah masih tersedia hingg 3 tahun mendatang dengan persentase 56,2% (Tabel 3).
Tabel 4. Jumlah Pengrajin Genteng dan Kemudahan Memperoleh Tanah Diolah
|
Frequency |
Percent |
Valid Percent |
Cumulative Percent | |
|
Valid Sangat mudah |
12 |
11.4 |
11.4 |
11.4 |
|
Mudah |
21 |
20.0 |
20.0 |
31.4 |
|
Cukup |
23 |
21.9 |
21.9 |
53.3 |
|
Sulit |
49 |
46.7 |
46.7 |
100.0 |
|
Total |
105 |
100.0 |
100.0 |
Pengrajin genteng di Desa Pejaten 46,7% merasa sulit memperoleh tanah diolah. Akses memperoleh tanah ini sangat dipengaruhi oleh interrelasi pengrajin dengan pemasok tanah.
Tabel 5. Jumlah Pengrajin Genteng Menurut Kemudahan Memperoleh Tanah Siap Cetak
|
Frequency |
Percent |
Valid Percent |
Cumulative Percent | |
|
Valid Sangat mudah |
2 |
1.9 |
1.9 |
1.9 |
|
Mudah |
5 |
4.8 |
4.8 |
6.7 |
|
Cukup |
17 |
16.2 |
16.2 |
22.9 |
|
Sulit |
48 |
45.7 |
45.7 |
68.6 |
|
Sangat sulit |
33 |
31.4 |
31.4 |
100.0 |
|
Total |
105 |
100.0 |
100.0 |
Untuk tanah siap cetak 45,7% merasa kesulitan memperoleh sumber daya tanah siap cetak dan 31,4% merasa sangat sulit. Informasi yang tersirat dari Tabel 2 sampai Tabel 6 memberikan informasi bahwa pengrajin genteng di Desa Pejaten lebih banyak merasa sulit memperoleh bahan baku utama genteng yaitu tanah liat.
Tabel 6. Jumlah Pengrajin Genteng Menurut Kecukupan Sumber Daya Tanah
|
Frequency |
Percent |
Valid Percent |
Cumulative Percent | |
|
Valid Banyak |
7 |
6.7 |
6.7 |
6.7 |
|
Cukup |
37 |
35.2 |
35.2 |
41.9 |
|
Kurang |
61 |
58.1 |
58.1 |
100.0 |
|
Total |
105 |
100.0 |
100.0 |
Pengrajin genteng di Desa Pejaten 58,1% memandang kecukupan tanah sebagai sumber daya produksi genteng kurang.
Model time series produksi genteng dibentuk berdasarkan data jumlah produksi
genteng 5 tahun terakhir yaitu Januari 2013 – Desember 2017, validasi model dilakukan
menggunakan data produksi Januari 2018 – Agustus 2018. Data produksi yang dicari
model time seriesnya adalah data jumlah produksi genteng di desa Pejaten dalam setiap
bulannya. Plot jumlah produksi genteng dari Januari 2013 hingga Desember 2017
ditampilkan dalam Gambar 1.
6000000
Month Jan
Data Produksi Genteng
18000000
16000000
14000000
12000000
10000000
8000000

Jan
Jan
Jan
Jan
2014
2015
2016
2017
Year 2013
Gambar 1. Plot Jumlah Produksi Genteng di Desa Pejaten
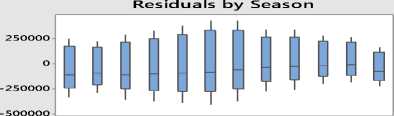
Plot jumlah produksi genteng memperlihatkan adanya pola tren dan musiman. Untuk mengetahui secara pasti pola trend an musiman pada data, digunakan metode dekomposisi klasik. Hasil dekomposisi klasik ditampilkan dalam Gambar 2.
Seasonal Analysis for Y Multiplicative Model
Seasonal Indices

Percent Variation by Season
12
8
4
0
Detrended Data by Season

1.25
1.00
0.75
0.50
1 2 3 4 5 6 7 8 9 10 11 12
1 2 3 4 5 6 7 8 9 10 11 12
6000000
Component Analysis for Y Multiplicative Model
Original Data
Detrended Data
15000000
12000000
9000000

2013
2013
2015
2016
2017
2013
2013
2015
2016
2017
Tahun
Tahun
2013
0.50
2013
Seasonally Adjusted Data
15000000
12000000
9000000
6000000
2013
2013
2013 2015 2016
Tahun
2017
Seas. Adj. and Detr. Data
250000
0
-250000
-500000

2013 2013 2013 2015 2016 2017
Tahun
Gambar 2. Dekomposisi Klasik Produksi Genteng
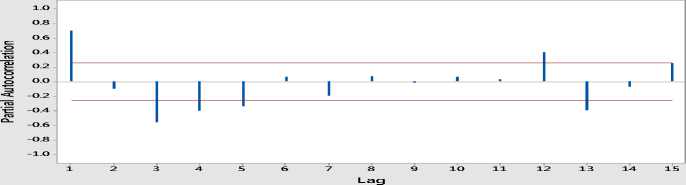
Plot dekomposisi deret waktu produksi genteng menunjukkan terdapat tren menurun serta pengaruh musiman pada data, karena adanya pola berulang secara teratur. Pengaruh musiman dan tren pada data produksi genteng menjelaskan bahwa data produksi genteng tidak stasioner. Hal ini dipertegas dengan memperhatikan plot ACF dan PACF data produksi genteng seperti ditampilkan pada Gambar 3.
PACF Produksi Genteng

Lag
Gambar 3. ACF dan PACF Produksi Genteng
Untuk mengetahui apakah data produksi genteng sudah stasioner dalam varians, dilihat dari plot transformasi Box-Cok pada Gambar 4.

Gambar 4. Transformasi Box- Cox Produksi Genteng Januari 2013 – Desember 2017
750
0
Data Produksi Genteng Diff
500
250
-250
-500

1 6 12 18 24 30 36 42 48 54 60
Index
120
100
80
60
40
20
0
-20
-40
Data Produksi Genteng Diff

1 6 12 18 24 30 36 42 48 54 60
Index
Gambar 5. Plot Deret Waktu Produksi Genteng Setelah Transformasi Log dan Diffrencing
Setelah ditransformasi log dan differencing, data produksi genteng menjadi stasioner. Selanjutnya ditentukan model ARIMA, dengan menentukan ACF dan PACF data produksi genteng yang sudah stasioner. Plot ACF dan PACF data produksi genteng yang sudah stasioner ditampilkan dalam Gambar 6.


Gambar 6. ACF dan PACF Produksi Genteng yang Stasioner
Berdasarkan plot ACF dan plot PACF untuk data yang telah ditransformasi, menunjukkan model ARIMA yang layak dicobakan yaitu ARIMA(1,1,1), ARIMA (1,1,2), ARIMA(1,1,4), ARIMA(1,1,5), ARIMA(3,1,1), ARIMA(3,1,2), ARIMA(3,1,4), ARIMA(3,1,5), ARIMA (4,1,1), ARIMA(4,1,2), ARIMA (4,1,4), dan ARIMA(3,1,5). Model ARIMA multiplikatif yang akan dicobakan diantaranya SARIMA(1,1,1)(1,1,1)12, SARIMA (1,1,2)(1,1,1)12, SARIMA(1,1,4)(1,1,1)12, dan SARIMA(1,1,5) (1,1,1)12. Estimasi model deret waktu dilakukan untuk ke-16 model yang diduga, kemudian dilakukan uji diagnostic (uji kecukupan model). Beberapa model yang diperkirakan tidak semuanya memenuhi asumsi sisaan white noise, pada Tabel 2 ditandai model-model yang memenuhi asumsi sisaan white noise.
Tabel 2. Uji Kecukupan Model Deret Waktu
|
No |
Model |
(p-value ) pada Lag | |||
|
12 |
24 |
36 |
48 | ||
|
1 |
ARIMA(1,1,1) |
0.000 |
0.000 |
0.000 |
0.000 |
|
2 |
ARIMA (1,1,2) |
0.000 |
0.000 |
0.000 |
0.000 |
|
3 |
ARIMA(1,1,4) |
0.000 |
0.000 |
0.000 |
0.000 |
|
4 |
ARIMA(1,1,5) |
0.000 |
0.000 |
0.000 |
0.000 |
|
5 |
ARIMA(3,1,1) |
0.000 |
0.000 |
0.000 |
0.000 |
|
6 |
ARIMA(3,1,2) |
0.000 |
0.000 |
0.000 |
0.000 |
|
7 |
ARIMA(3,1,4), |
0.000 |
0.000 |
0.000 |
0.000 |
|
8 |
ARIMA(3,1,5) |
0.000 |
0.000 |
0.000 |
0.000 |
|
9 |
ARIMA (4,1,1) |
0.000 |
0.000 |
0.000 |
0.000 |
|
10 |
ARIMA(4,1,2) |
0.000 |
0.000 |
0.000 |
0.000 |
|
11 |
ARIMA (4,1,4) |
0.000 |
0.000 |
0.000 |
0.000 |
|
12 |
ARIMA(3,1,5) |
0.000 |
0.000 |
0.000 |
0.000 |
|
13 |
SARIMA(1,1,1)(1,1,1)12 |
0.028 |
0.376 ** |
0.842 ** |
* |
|
14 |
SARIMA(1,1,2)(1,1,1)12 |
0.143 ** |
0.736 ** |
0.969 ** |
* |
|
15 |
SARIMA(1,1,4)(1,1,1)12 |
0.041 |
0.558 ** |
0.927 ** |
* |
|
16 |
SARIMA(1,1,5) (1,1,1)12 |
0.118 ** |
0.796 ** |
0.975 ** |
* |
Dari enam belas model yang diperiksa, dengan menetapkan taraf nyata 5% hanya dua model multiplikatif yang memenuhi white noise artinya tidak ada korelasi antar residual. Kedua model selanjutnya yang diselidiki signifikansi model dan sisaannya apakah berdistribusi normal. Selanjutnya nilai estimasi parameter, p-value model SARIMA(1,1,2)(1,1,1)12 dan model SARIMA(1,1,5) (1,1,1)12 disajikan pada Tabel 3.
Tabel 3. Estimasi Parameter Model Sarima Produksi Genteng Pejaten
|
Model SARIMA |
Non Musiman |
Musiman | ||
|
Estimasi Parameter |
p-value |
Estimasi Parameter |
p-value | |
|
SARIMA(1,1,2)(1,1,1)12 |
ϕ1 = 0,5033 |
0,404 |
Φ1 = -1,0145 |
0,000 |
|
θ1 = 0,5183 |
0,387 |
Θ1 = -0,9226 |
0,000 | |
|
θ2 = -0,1886 |
0,239 | |||
|
Residuals: SS = |
6452,28 (backforecasts excluded) | |||
|
MS = 153,63 DF = 42 | ||||
|
SARIMA(1,1,5) (1,1,1)12. |
ϕ1 = 0,9326 |
0,000 |
Φ1 = -1,0185 |
0,000 |
|
θ1 = 1,0120 |
0,000 |
Θ1 = -0,9491 |
0,000 | |
|
θ2 = -0,2925 |
0,209 | |||
|
03 = 0,1825 |
0,414 | |||
|
04 = -0,2349 |
0,292 | |||
|
05 = 0,2813 |
0,082 | |||
|
Residuals: SS = |
5793,08 (backforecasts excluded) | |||
|
MS = |
148,54 DF = |
39 | ||
Model SARIMA(p,d,q)(P, D,Q) dinyatakan sebagai:
Φp (B)Φ P(Bs) (1-B)d(1-Bd) Xt = (B)ΘQ(Bs) at
Berdasarkan identifikasi model estimasi yang diperoleh, maka model deret waktu (time series) jumlah produksi genteng di Desa Pejaten adalah model SARIMA(1,1,5) (1,1,1)12.
Model SARIMA(1,1,5) (1,1,1)12 dinyatakan sebagai:
Φl (B)Φi(B12) (1-B)1(1-B1) Xt = (B)Θi(B12) at
Dengan nilai-nilai parameter model Φι = 0,9326; Bi = 1,0120; @2 = -0,2925; = 0,1825; B4 = -0,2349; B5 = 0,2813; Φ1 = -1,0185; Θ1 = -0,9491. Model ini
memberikan nilai SS = 5793.08 dan MS = 148,54.
Semua pengrajin genteng di Desa Pejaten memperoleh tanah dengan membeli tanah cangkul per truk, kemudian diolah menjadi tanah liat yang siap dicetak. Pengrajin genteng sebagian besar menyatakan bahwa supply tanah masih tersedia hingg 3 tahun mendatang dengan persentase 56,2%.
Model peramalan produksi genteng dengan keterbatasan sumber daya yang ada dengan analisis deret waktu diperoleh model deret waktu jumlah produksi genteng di Desa Pejaten adalah model SARIMA(1,1,5) (1,1,1)12. Model SARIMA(1,1,5) (1,1,1)12 dinyatakan sebagai:
Φι (B)Φi(B12) (1-B)1(1-B1) Xt = (B)Θi(B12) at
dengan nilai-nilai parameter model Φι = 0,9326; Bi = 1,0120; B2 = -0,2925; = 0,1825; B4 = -0,2349; Bs = 0,2813; Φ1 = -1,0185; Θ1 = -0,9491. Model ini memberikan nilai SS = 5793.08 dan MS = 148,54.
Ucapan Terima Kasih
Terima kasih diucapkan kepada pimpinan Fakultas MIPA atas bantuan dana pada penelitian ini, terima kasih pada pimpinan Universitas Udayana dan LPPM atas kesempatan yang diberikan. Pendanaan penelitian melalui DIPA BLU Universitas Udayana Sesuai dengan Surat Perjanjian Kerja Pelaksanaan Kegiatan Penelitian Unggulan Program Studi Nomor: 3779/UN14.2.8.II/LT/2018, tanggal 28 Mei 2018
Daftar Pustaka
Abraham, B. & Ledolter, J. 2005. Statistical Methods for Forecasting. New Jersey: John
Wiley and Sons.
Bowerman, Richard, T., Bruce, L., O’Connell., and Koehler, A.B. 2005. Forecasting, Time Series, and Regression :An Applied Approach. 4th Ed. Boston :Brooks/Cole.
Box, G.E., Jenkins, G.M., Reinsel, G.C., & Ljung, G.M. 2016. Time Series Analysis :
Forecasting, Time Series, and Control. 5th Ed. San Francisco : John Wiley and Sons.
Makridakis, S., Wheelwright, S.C., & McGee, V.E., 1999. Metode dan Aplikasi
Peramalan Jilid 1. 2nd Ed. Jakarta: Erlangga.
Nurbawa, M. 2017. Jejak Genteng di Tanah Pejaten-Dari Era Barter Hingga Zaman
Pariwisata. http://tatkala.co/2017/05/05/jejak-genteng-di-tanah-pejaten-dari-era-
barter-hingga-zaman-pariwisata/.Online :diakses 20 Januari 2018.
Wei, W.W. 2006. Time Series Analysis : Univariate and Multivariate Methods. 2nd
Ed. New York :Pearson Addison Wesley
138
Discussion and feedback