Metoda Autoregressive untuk Peramalan Jangka Panjang
on
Jurnal Matematika Vol. 8 No.2, Desember 2018, pp.121-125
Article DOI: 10.24843/JMAT.2018.v08.i02.p104
ISSN: 1693-1394
Metoda Autoregressive untuk Peramalan Jangka Panjang
Ria Faulina
STKIP PGRI Bangkalan
Email: riafaulina@stkippgri-bkl.ac.id
Abstract: Changes in seasonal patterns in Indonesia are closely related to rainfall.
Various forecasting techniques were developed to produce better accuracy. In this study ARIMA linear forecasting techniques were used. The data used is secondary data from BMKG Kalianget Station, Sumenep from January 2008 - December 2017 with a monthly rainfall research variable. To measure the accuracy of the forecast results used by RMSE.From the result of this study, ARIMA ([1,6],0,0)(0,1,1)12providing better accuracy than ARIMA (1,0,0)(0,1,1)12 for predicting the next 1 month or 12 months (a year ahead).
Keywords: Curah hujan, ARIMA, preprocessing, RMSE
Letak geografis Indonesia yang berada di garis khatulistiwa mempengaruhi pola perubahan iklim di Indonesia. Perubahan iklim memberikan dampak serius seperti banjir, kekeringan, longsor, angin kencang, dan lain sebagainya. Untuk mengantisipasi hal tersebut perlu adanya prediksi iklim sebagai peringatan dini.
Berbagai teknik peramalan telah dikembangkan salah satunya pada peramalan curah hujan. Metode peramalan yang dikembangkan terdiri dari metode linier dan non-linier hingga modifikasi dari model-model peramalan yang ada.Seperti pada penelitian Abraham dan Nath (2001); Chang, Wei, Cheng (2011); Dalam penelitian Faulina (2018) model ARIMA lebih baik dibandingkan dengan teknik peramalan hibrida ARIMA – ANFIS. Hal ini menunjukkan metode yang lebih kompleks tidak selalu lebih baik dibandingkan model ARIMA biasa. Oleh karena itu, dalam penelitian ini digunakan model ARIMA untuk memprediksi curah hujan pada bulan berikutnya.
Dalam penelitian ini digunakan model peramalan ARIMA. ARIMA dibedakan menjadi model non-musiman dan model musiman. Dua tipe ARIMA yang dikenal adalah model autoregressive dan moving average (Wei, 2006). Model non-musiman terdiri dari AR (p), MA (q), ARMA (p,q), dan ARIMA (p,d,q). Dari keempat model tersebut, dapat dikelompokkan menjadi dua, yaitu model stasioner dan model non-stasioner. AR(p), MA(q), dan ARMA (p,q) merupakan model stasioner. Sedangkan ARIMA (p,d,q) adalah model non-stasioner.
Secara umum, model ARIMA adalah:
∅V(B)Φp(Bs)(1-B)d(1-Bs)Dzt = (B)ΘQ(Bs) at (1)
dimana
∅p(B)=1-∅^B -∅2B2-⋯- ∅p Bv adalah koefisien komponen AR non musiman dengan orde p
Φp(B)s= koefisien komponen AR musiman s dengan orde p
θq (B) = 1-Θ1B - Θ2B2-⋯-θqBqadalah koefisien komponen MA non-musiman dengan orde q
ΘQ(Bs) = koefisien komponen MA musiman S dengan orde Q
dl- = error white noise CL^ ~IIDN (0, σa )
B = operator Backward
(1-B)d = pembeda non-musiman dengan orde d
(1-Bs)d= pembeda musiman dengan orde D
Data yang digunakan merupakan data sekunder yang didapatkan melalui website resmi Badan Meteorologi Klimatologi dan Geofisika dengan variabel yang digunakan adalah curah hujan. Data yang digunakan adalah data bulanan dari bulan Januari 2008–Desember 2017. Dalam teknik peramalan, data dibagi menjadi dua yaitu data training dan data testing. Data training digunakan untuk membentuk model sedangkan data testing untuk pengukuran akurasi. Data yang digunakan untuk tahap training adalah data pada bulan Januari 2008 sampai dengan Desember 2016. Sedangkan untuk pemilihan peramalan terbaik (testing) digunakan data pada bulan Januari 2017–Desember 2017. Adapun langkah-langkah peramalan dalam penelitian adalah sebagai berikut.
-
a) Mempersiapkan data training dan data testing.
-
b) Melakukan identifikasi visual melalui plot time series, ACF, dan PACF pada data training
-
c) ACF dan PACF digunakan untuk identifikasi kestasioneran data dan inisial model ARIMA
-
d) Jika data tidak stasioner dilakukan differencing dan dilakukan plot ACF dan PACF terhadap data yang telah di-differencing.
-
e) Melakukan perhitungan akurasi ramalan data testingdengan persamaan sebagai berikut.
RMSE =√
∑ ⅛ | ̂i- z1 | 1 n
Tahap awal dalam teknik peramalan adalah identifikasi data secara visual. Berikut plot time series data curah hujan rata-rata bulanan di Kabupaten Sumenep.

Gambar 1. Plot Time Series Curah Hujan Rata-Rata Bulanan
Dari Gambar 1 terlihat bahwa terdapat pola fluktuatif yang menunjukkan kecenderungan pola musiman. Identifikasi selanjutnya adalah menggunakan plot ACF dan PACF pada data tersebut.

Lag

Gambar 2. ACF dan PACF Curah Hujan Rata-Rata Bulanan
Pada Gambar 2 plot ACF menunjukkan adanya pola turun lambat pada lag kelipatan 12. Hal ini mengindikasikan gejala ketidakstasioneran dalam data. Oleh karena itu, perlu adanya differencing untuk mengatasi masalah tersebut.

Lag
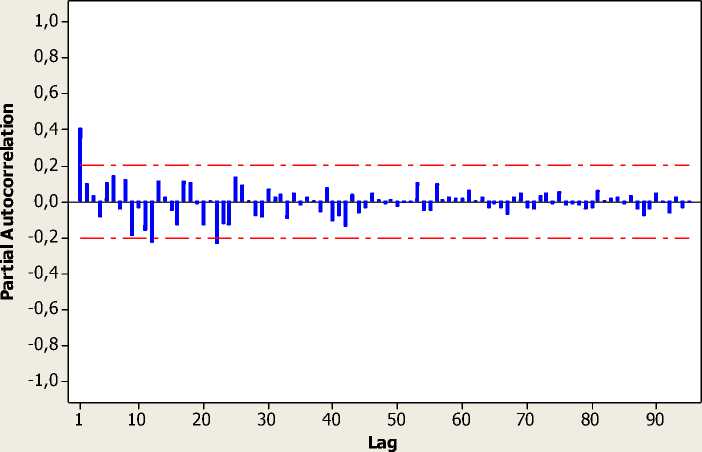
Gambar 3. ACF dan PACF Curah Hujan Rata-Rata Bulanan Setelah Differencing 12
Dari Gambar 3 dengan differencing lag 12 plot curah hujan rata-rata bulanan setelah preprocessing telah stasioner. Selanjutnya adalah menentukan inisial model ARIMA berdasarkan plot ACF dan PACF Gambar 3. Untuk menentukan inisial model ARIMA, dapat dilihat dari lag yang berada diluar batas signifikansi pada plot ACF adalah lag : 1, 2, dan 12 sedangkan pada plot PACF Lag yang berada diluar batas signifikansi adalah : 1, 12, dan 22. Adapun model akhir untuk curah hujan rata-rata bulanan adalah model yang memenuhi asumsi residual white noise dan berdistribusi normal serta signifikansi estimasi parameter.
Tabel 1. Model ARIMA Curah Hujan Rata-Rata Bulanan Setelah Preprocessing Data
|
Model ARIMA |
Keterangan |
|
Model Awal : |
Terdapat beberapa estimasi parameter model |
|
ARIMA(2, 0, 1) (1,1,1)12 |
tidak signifikan, Asumsi white noise dan |
|
normalitas error tidak terpenuhi | |
|
Model Akhir : |
Estimasi parameter model signifikan, Asumsi |
|
ARIMA (1,0,0) (0,1,1)12 |
white noise dan normalitas error terpenuhi |
ARIMA ([1,6],0,0)(0,1,1)12
Adapun evaluasi akurasi peralaman curah hujan rata-rata bulanan di Kab. Sumenep ditunjukkan pada Tabel 2.
Tabel 2. Perbandingan Akurasi Ramalan berdasarkan RMSE
|
Model |
1 step |
12 step |
|
ARIMA (1,0,0)(0,1,1)12 |
6,109 |
4,286 |
|
ARIMA ([1,6],0,0)(0,1,1)12 |
4,075 |
4,245 |
Dari hasil yang ditunjukkan pada Tabel 2, 1 step adalah hasil akurasi ramalan 1 bulan berikutnya, sedangkan 12 step adalah hasil akurasi ramalan 12 bulan berikutnya. Model ARIMA ([1,6],0,0)(0,1,1)12 memberikan akurasi lebih baik dibandingkan model ARIMA (1,0,0)(0,1,1)12baik untuk meramalkan 1 bulan berikutnya ataupun 12 bulan atau 1 tahun ke depan.
Dari hasil analisis diatas, dari model ARIMA yang diperoleh, untuk meramalkan 1
12 bulan ataupun 1 tahun ke depan lebih baik menggunakan model ARIMA ([1,6],0,0)(0,1,1)12 dibandingkan ARIMA (1,0,0)(0,1,1). Perlu adanya penelitian lanjut tentang metode ARIMA yang mampu menangkap efek outlier pada data curah hujan mengingat pada data iklim khususnya curah hujan sering dijumpai data-data yang ekstrim.
Daftar Pustaka
Abraham, A., dan Nath, B. (2001). A neuro-fuzzy approach for modelling electricity demand in Victoria. Applied Soft Computing, Vol I, hal 127-138.
Chang, J. R., Wei, L. Y., & Cheng, C. H. (2011). A Hybrid ANFIS Model Based on AR and TAIEX Forecasting. Applied Soft Computing, 1388-1395.
Faulina, R., & Aini, N. (2018). Metode Hibrida Berbasis Preprocessing Data Untuk Peramalan Curah Hujan Jangka Panjang. SOULMATH, Vol 6, No.2, hal 105-112.
Liu, J., Wang, X., & Lu, Y. (2017). A novel hybrid methodology for short-term wind power forecasting. Renewable Energy, 103, 620-629.
Wei, W.W.S. (2006). Time Series Analysis, Univariate and Multivariate Methods. Canada : Addison Wesley Publishing Company
125
Discussion and feedback