Implementasi Model Fungsi Transfer dan Neural Network untuk Meramalkan Harga Penutupan Saham (Close Price)

Jurnal Matematika Vol. 9, No.1, Juni 2019, pp. 11-25

Article DOI: 10.24843/JMAT.2019.v09.i01.p107

ISSN: 1693-1394

Implementasi Model Fungsi Transfer Dan Neural Network untuk Meramalkan Harga Penutupan Saham (Close Price) (Studi Kasus: PT. Bank Central Asia, Tbk)

Nila Rahmawati

Universitas Negeri Malang e-mail: [email protected]

Trianingsih Eni Lestari

Universitas Negeri Malang e-mail: [email protected]

Abstract: The multivariate forecasting model is a model that pays attention to the relationship between predicted factor and one or more independent variabels. This research uses multivariate forecasting model involving transfer function model as well as neural network. Transfer function model and neural network both are used to predict the close price data by considering the influencing data on the open price as independent variabels of forecasting model. The data being used in this research is price data of close price and that of monthly open price in PT. Bank Central Asia, Tbk. The best model to forecast the close price is the transfer function model having MSE, MAPE, and MAE’s smaller values than those of neural network.

Keywords: transfer function, neural network, stock open price, stock close price

• 1.    Pendahuluan

Harga penutupan saham (close price) merupakan harga yang terpenting dalam perdagangan saham di bursa efek. Samsul [1] menjelaskan bahwa harga penutupan saham (close price) dapat dijadikan dasar untuk membentuk indeks harga saham yang berkaitan dengan return saham. Return saham merupakan salah satu model pengambilan keputusan investor untuk membeli atau menjual saham. Pada kenyataannya, pergerakan harga pembukaan saham (open price) yang tidak menentu pada awal pembukaan perdagangan sampai perdagangan berakhir akan memberikan pengaruh terhadap harga penutupan saham (close price). Dengan demikian, diperlukan analisis untuk melihat pola hubungan pergerakan harga saham yang dikeluarkan oleh bursa efek. Analisis yang

digunakan adalah analisis deret waktu dengan menggunakan model peramalan multivar-iat yaitu, model fungsi transfer dan neural network.

Peramalan deret waktu dengan model fungsi transfer pernah dilakukan oleh Nurini, et. al. [2] untuk meramalkan harga tertinggi (high price) dan harga terendah (low price) dengan variabel inputnya yaitu harga pembukaan pada data indeks harga saham gabungan (IHSG) Nikkei 255. Penelitian yang sama juga pernah dilakukan oleh Purnama, et. al [3] untuk meramalkan curah hujan di Kota Batu.

Makridakis, et. al. [4] menjelaskan bahwa model fungsi transfer merupakan model yang menggambarkan nilai-nilai prediksi dari suatu deret berkala (disebut deret output) yang didasarkan pada nilai-nilai masa lalu dari deret itu sendiri (deret output) dan satu atau lebih deret berkala yang berhubungan (disebut dengan deret input) dengan deret output tersebut. Selain itu, Wei [5] juga menjelaskan bahwa pada model fungsi transfer terdapat deret output yang diperkirakan akan dipengaruhi oleh deret input dan input-input lain yang digabungkan dalam satu kelompok yang disebut gangguan atau noise (n_l) . Pembentukan model fungsi transfer diawali dengan dengan membentuk model ARIMA pada data input.

• a. Model ARIMA

Wei [5] menjelaskan bahwa model ARIMA merupakan model ARMA(P,Q) yang nonstationer. Pada model ARMA(P,q) nonstationer, proses pembedaan (differencing) dilakukan agar stationer. Setelah model ARMA(P,q) mengalami proses pembedaan sebanyak d kali hingga stationer, maka model ARMA(P,q) menjadi model ARI-MA( P,d,q). Model ARIMA(P,d,q) ditulis dalam persamaan berikut:

φ_p(B)(l-B)^dX_t=μΛθ_q(B)a_t

(1)

dengan:

Φ_p(B)

(1 - B)^d O_q(B)

: Parameter AR orde P dimana,

Φ_p(b) = i-φ₁b-φ₂b² -

: Differencing dengan orde cl : Parameter MA orde q dimana,

φ_p(B) = l-θ₁B-θ₂B²-∙

~Φ_pB^p

-θ_qB^t*

^a_t

b.

: Nilai residual (nilai kesalahan) pada waktu ke—t yang dianggap berdistribusi normal identik independen dengan rataanya 0 dan varians konstan.

Model Fungsi Transfer

Makridakis, et. al. [4] menjelaskan bahwa secara umum, model fungsi transfer

dapat ditulis sebagai berikut.

y_t = v(B)x_t + n_t

dimana:

y_t : Deret output

√B)

: Fungsi bobot respon impuls, biasanya ditulis dengan

v(B) = (v₀ + v₁B +v₂B + - +v_kB^k)

dimana X adalah orde fungsi transfer, V_k adalah bobot respon impuls pada

lag k , dan B adalah operator mundur

^t     : Deret input

n_t : Pengaruh kombinasi dari seluruh faktor yang mempengaruhi Y_t, dan disebut dengan gangguan (noise).

Makridakis, et. al. [4] menjelaskan bahwa orde fungsi transfer adalah K akan menjadi orde tertinggi untuk proses pembedaan sehingga, model fungsi transfer dapat dituliskan dalam model sebagai berikut.

^B^)

(2)

(3)

^W^”'

ω(B) Θ(B)

^yt ~~δ^^xt~^{b +} φ(B)^at

dimana:

"(5) :

S(B^) : θ(β') : Φ(E) : y_t     : Nilai deret output yang telah ditransformasikan dan dibedakan

^t     : Nilai deret input yang telah ditransformasikan dan dibedakan

^t : Nilai gangguan (noise) random r,s,P,q dan b adalah konstanta.

Penelitian terdahulu tentang model neural network untuk peramalan data deret waktu pernah dilakukan oleh Elsafi [6] untuk meramalkan kecepatan aliran air Sungai Nil di Stasiun Dongola. Penelitian yang sama juga pernah dilakukan oleh Ayodele, et. al. [7] untuk meramalkan harga saham.

Model neural network merupakan model yang disusun dari tiga lapisan yaitu, lapisan input yang terhubung dengan lapisan tersembunyi (hidden layer), dimana lapisan tersembunyi (hidden layer) ini juga terhubung dengan lapisan output. Setiap lapisan ini akan dihubungkan melalui neuron atau node. Neural network dilatih untuk melihat hubungan antara lapisan input dan lapisan output (Stergiou & Siganous dalam Elsafi, [6]).

Jaringan feedforward neural network adalah salah satu model neural network yang banyak digunakan untuk memprediksi data deret waktu. Model feedforward neural network ini menggunakan algoritma pelatihan backpropagation (propagasi balik). Suyanto [8] menjelaskan bahwa algoritma backpropagation ini melakukan dua tahap perhitungan yaitu, perhitungan maju untuk menghitung galat antara keluaran aktual dan

target dan perhitungan mundur yang mempropagasikan balik galat tersebut untuk memperbaiki bobot-bobot sinaptik pada semua neuron yang ada.

Crone, et. al. [9] menjelaskan bahwa dalam menentukan jumlah variabel pada lapisan input ditentukan lag yang signifikan pada PACF data deret waktu. Selanjutnya, data deret waktu yang digunakan untuk peramalan akan dibagi menjadi 2 yaitu, data training dan data testing. Pembagian data training dan data testing ini berdasarkan pada aturan yang sering digunakan yaitu, 90% untuk data training dan 10% untuk data testing, 80% untuk data training dan 20% untuk data testing, atau 70% untuk data training dan 30% untuk data testing, dll (Zhang, et. al., [10]).

Selain itu, Zhang, et. al. [10] menjelaskan bahwa normalisasi data dapat dilakukan sebelum melakukan tahapan pelatihan (training). Normalisasi data ini dilakukan agar data input maupun data output berada pada rentangan nilai tertentu. Adapun normalisasi data yang digunakan adalah transformasi linier ke [0,1]. Transformasi linier yang digunakan dengan rentangan nilai antara 0 sampai 1 menggunakan persamaan (Lapedes et al dalam Zhang, et. al., [10]):

_{z s=} (Z_t-Z(min)) (z (max) — Z(min))

dimana:

%             : Data deret waktu hasil normalisasi

^ t           : Data deret waktu yang sebenarnya

Z(max)      : Nilai maksimum dari data deret waktu

Z (min)      : Nilai minimum dari data deret waktu.

Banyaknya neuron pada lapisan tersembunyi (hidden layer) berada di antara (2n + 1) sampai dengan (2√n + m) dimana, n adalah banyaknya neuron pada lapisan input dan m adalah banyaknya neuron pada lapisan output (Fletcher, et. al., [11]). Pada lapisan tersembunyi (hidden layer) ini fungsi aktivasi yang sering digunakan adalah fungsi sigmoid biner. Nilai output dari fungsi sigmoid biner ini terletak antara 0 sampai 1 (Fausett, [12]). Sedangkan, fungsi aktivasi yang digunakan pada lapisan output adalah fungsi linear atau purelin. Fungsi linear atau purelin merupakan fungsi yang memiliki nilai output sama dengan nilai inputnya.

Zhang [13] menjelaskan bahwa persamaan dari model neural network untuk peramalan data deret waktu adalah sebagai berikut:

dimana:

^ t    : Data deret waktu pada periode ke t

^ t—Z   : Data deret waktu pada periode ke t Jc

g^h(x) : Fungsi aktivasi pada lapisan tersembunyi (hidden layer)

Aq : Bias pada lapisan output

^aJ     : Bobot pada lapisan output

βfti : Bias pada lapisan tersembunyi (hidden layer)

^i j : Bobot pada lapisan tersembunyi (hidden layer)

• ■-       : 0, 1, 2, 3, ..., V dimana, P merupakan banyaknya neuron pada lapisan input

• }      : 0, 1, 2, 3, ..., q dimana, q merupakan banyaknya neuron pada lapisan

tersembunyi (hidden layer)

e_t : Nilai sisaan model.

Penelitian dengan menggunakan model fungsi transfer dan neural network juga pernah dilakukan oleh Ma’rufah, et. al. [14]. Pada penelitian tersebut, dilakukan perbandingan model fungsi transfer dan model neural network pada variabel input biaya dana dan Loan to Deposit Ratio (LDR) untuk meramalkan pendapatan bunga bank BRI dan BCA. Hasil dari penelitian tersebut menunjukkan bahwa model fungsi transfer lebih baik digunakan untuk meramalkan pendapatan bunga bank BRI. Sedangkan, model neural network lebih baik digunakan meramalkan pendapatan bunga bank BCA.

Sejalan dengan penelitian yang pernah dilakukan oleh Ma’rufah, et. al. [14],

maka pada penelitian ini akan membandingkan model fungsi transfer dan model neural network untuk meramalkan harga penutupan saham (close price) di PT. Bank Central Asia, Tbk. Hal yang akan diteliti berkaitan dengan pergerakan harga pembukaan saham (open price) dan harga penutupan saham (close price) pada setiap periodenya. Pada model fungsi transfer dan model neural network output yang diharapkan adalah hasil peramalan harga penutupan saham (close price) dengan melihat pengaruh dari data harga pembukaan saham (open price) sebagai data inputnya.

Pemilihan model peramalan terbaik pada penelitian ini menggunakan beberapa uji ketepatan perkiraan antara lain:

a.

b.

c.

Nilai tengah kesalahan kuadrat/ Mean Squared Error (MSE)

(5)

Nilai tengah kesalahan persentase absolute/Mean Absolute Percentage Error

(MAPE)

∑r=ι ∣⅛^a∣

MAPE =---¹--— X 1OO%                 (6)

Nilai tengah kesalahan absolute/Mean Absolute Error (MAE)

_MAE = ⅛Ξ⅛I                (7)

dimana Z_i adalah data aktual, Z_i adalah nilai perkiraan, dan Yt adalah banyaknya perkiraan. Model peramalan yang paling baik umumnya adalah model yang memiliki nilai kesalahan yang terkecil (Makridakis, et. al., [14]).

• 2.    Metode Penelitian

Data yang digunakan dalam penelitian ini adalah data sekunder yaitu data harga saham (open price) dan data harga penutupan saham (close price) pada PT. Bank Central Asia, Tbk. Data tersebut diperoleh dengan cara mengunduh dari situs: http://finance.yahoo.com. Adapun data yang digunakan dalam penelitian ini adalah data dari bulan Januari 2010 sampai dengan bulan Juli 2017.

Langkah-langkah analisis data yang dilakukan pada penelitian ini adalah sebagai berikut:

• 1.    Membuat statistik deskriptif untuk masing-masing data yaitu data harga pembukaan (open price) dan data harga penutupan (close price) untuk mengetahui karakteristik data harga saham pada PT. Bank Central Asia, Tbk.

• 2.    Membagi data menjadi dua bagian, yaitu data input dan data output. Pada pemodelan fungsi transfer, data harga pembukaan saham (open price) digunakan sebagai data input dan data harga penutupan saham (close price) digunakan sebagai data output. Sedangkan pada pemodelan neural network, penentuan data input dan output berdasarkan plot PACF dari data harga pembukaan saham (open price) dan data harga penutupan saham (close price).

• 3.    Memodelkan data harga pembukaan saham (open price) dan data harga penutupan saham (open price) dengan menggunakan metode fungsi transfer dan neural network.

• 4.    Meramalkan data harga penutupan saham (close price) dengan menggunakan model fungsi transfer dan neural network untuk beberapa periode yang akan datang.

• 5.    Menentukan model terbaik antara model fungsi transfer dan model neural network untuk meramalkan harga penutupan saham (close price) pada PT. Bank Central Asia, Tbk berdasarkan nilai error yang terkecil.

• 3.    Hasil dan Pembahasan
  
  3.1    Pembentukan Model Fungsi Transfer

Langkah pertama sebelum membentuk model fungsi transfer adalah membentuk model ARIMA untuk data input yaitu data harga pembukaan saham (open price) pada PT. Bank Central Asia, Tbk. Pembentukan awal model ARIMA untuk data input dil-

akukan dengan uji stationeritas terhadap varians. Uji stationeritas terhadap varians pada data input dapat dilihat melalui plot transformasi Box-Cox. Plot transformasi Box-Cox dari data input ditunjukkan pada gambar di bawah ini:

Box-Cox Plot of Open

Lambda

(using 95,0% confidence)

Estimate            0,47

Lower CL        -0,06

Upper CL        1,04

Rounded Value   0,50

Gambar 1. Plot transformasi Box-Cox pertama

Berdasarkan Gambar 1 tersebut dapat diketahui bahwa nilai lambda atau rounded value-nya menunjukkan angka 0,50 yang mengindikasikan bahwa data input belum stationer dalam varians. Oleh karena itu, perlu dilakukan transformasi Box-Cox kembali. Hasil transformasi Box-Cox ditunjukkan pada gambar di bawah ini:

Box-Cox Plot of Trans 1

Lambda

(using 95,0% confidence)

Estimate0,93

Lower CL-0,07

Upper CL2,05

Rounded Value1,00

Gambar 2. Plot transformasi Box-Cox kedua

Berdasarkan Gambar 2 tersebut dapat diketahui bahwa nilai lamda atau rounded value-nya telah menunjukkan angka 1,00 yang mengindikasikan bahwa data input atau data harga pembukaan saham (open price) sudah stationer dalam varians.

Langkah selanjutnya, dilakukan uji stationeritas terhadap rata-rata. Untuk mensta-tionerkan dalam rata-rata pada data input dilakukan melalui proses differencing. Selanjutnya, akan dilakukan uji Augmanted Dickey-Fuller untuk melihat apakah data input tersebut perlu dilakukan proses differencing kembali atau tidak. Berdasarkan hasil uji Augmanted Dickey-Fuller diperoleh bahwa nilai t — statistic sebesar -10,51270. Nilai t — statistic ini kurang dari nilai kritis a = 0,05 sebesar –3,461094. Oleh karena itu, dapat dikatakan bahwa data tersebut sudah stationer dalam rata-rata.

Berdasarkan hasil analisis dengan melakukan identifikasi model diperoleh beberapa model ARIMA sementara yaitu, ARIMA(0,1,1), ARIMA(1,1,0), dan ARI-MA(1,1,1). Hasil uji signifikansi parameter, uji diagnostik yang meliputi, uji white noise residual dan uji normalitas residual maka diperoleh model ARIMA untuk data input yaitu ARIMA(1,1,1) dengan model yaitu:

x_f = l,74x_r.₁ — 0,74x_f., + α,- 0,9735«, ,

Prewhitening untuk data input diperoleh persamaan yaitu

α = x, — l,74x,₁ + 0,74x_f., + 0,9735«, , LL         L X,    ^a    L Xi            LX

Sedangkan, prewhitening untuk data output diperoleh persamaan yaitu:

β_t = y_t - V⁴Yt-I + 0,74y_t-₂ + O,97350_t~₁

(S)

(9)

(10)

Setelah dilakukan prewhitening terhadap data input dan data output, kemudian akan ditentukan orde b,r , dan s berdasarkan plot CCF untuk menduga model awal fungsi transfer. Model sementara dari b,r,s yaitu (2,2,2), (2,2,1), (2,1,1), (2,1,0), dan (2,0,0). Sedangkan, pembentukan model ARIMA untuk deret noise dilakukan dengan mengidentifikasi plot ACF dan plot PACF. Berdasarkan hasil identifikasi terhadap plot ACF dan PACF diperoleh model ARIMA untuk deret noise yaitu, ARIMA(0,0,1), ARIMA(0,0,2), ARIMA(1,0,0), dan ARIMA(1,0,1). Berdasarkan hasil uji signifikansi parameter, uji white noise residual, dan uji normalitas residual diperoleh model ARIMA terbaik untuk deret noise yaitu, ARIMA(1,0,0).

Hasil dari pendugaan nilai b,r,s serta pada model ARIMA untuk deret noise maka, diperoleh model sementara fungsi transfer (b, r,s) (p, 0,q) adalah model fungsi transfer (2,2,2)(1,0,0), (2,2,1)(1,0,0), (2,1,1)(1,0,0), (2,1,0)(1,0,0), dan (2,0,0)(1,0,0). Berdasarkan hasil uji signifikansi parameter dan pemeriksaan diagnostik yang meliputi pemeriksaan nilai autokorelasi residual dan korelasi silang residual deret input yang telah di prewhitening diperoleh model fungsi transfer terbaik adalah (2,0,0)(1,0,0). Hasil dari estimasi parameter model fungsi transfer (2,0,0)(1,0,0) akan dijelaskan pada Tabel 1 berikut ini.

Tabel 1. Estimasi Parameter Fungsi Transfer (2,0,0)(1,0,0)

Parameter	Estimate	Standard Error	^value	P value
AR1,1 (Φl)	0,98775	0,02243	44,04	< 0,0001
NUM1 (*⅛)   \	0,23672	0,11179	2,12	0,0342

Pada persamaan tersebut terlihat bahwa model peramalan fungsi transfer untuk data penutupan saham (close price) pada periode ke t dipengaruhi oleh data penutupan saham (close price) pada periode ke t- 1, data pembukaan saham (open price) pada periode ke t - 2 dan periode ke t - 3 serta nilai sisaan pada periode ke t.

• 3.2    Pembentukan Model Neural Network

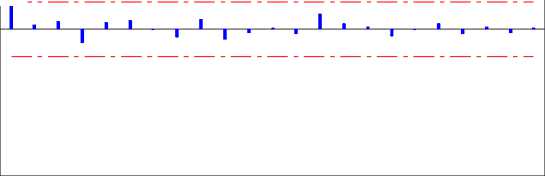
Pembentukan model neural network digunakan jaringan feedforward neural network dengan algoritma backpropagation. Penentuan data input dan data target dilakukan dengan mengidentifikasi plot PACF pada data harga pembukaan saham (open price) dan data penutupan saham (close price) yang ditunjukkan pada gambar di bawah ini:

Partial Autocorrelation Function for Open (with 5% significance limits for the partial autocorrelations)

Gambar 3. Plot PACF data harga pembukaan saham (open price)

Partial Autocorrelation Function for Close (with 5% significance limits for the partial autocorrelations)

1,0

0,8

.2

ro α;

.s

0,6

0,4

0,2

2     4     6     8     10    12    14    16    18    20    22

Lag

0,0

-0,2

-0,4

D. -0,6

-0,8

-1,0

Gambar 4. Plot PACF data harga penutupan saham (close price)

Berdasarkan plot PACF diperoleh data input yang digunakan adalah data harga pembukaan saham (open price) pada periode ke t- 1 dan data harga penutupan saham (close price) pada periode ke t - 1 . Sehingga, data input yang digunakan adalah sebagai data harga pembukaan saham (open price) pada periode ke t- 1 dan 1 sebagai data harga penutupan saham (close price) pada periode ke t - 1. Sedangkan, data target yang digunakan adalah data harga penutupan saham (close price) pada periode ke t . Oleh karena itu, data input yang digunakan pada penelitian ini sebanyak 2 data dan data targetnya sebanyak 1 data. Selanjutnya, data akan dibagi menjadi 80% data training dan 20% data testing dan akan dilakukan normalisasi terhadap data tersebut.

Model jaringan feedforward neural network menggunakan fungsi gradient descent dengan momentum dan fungsi pelatihan traingdx. Sedangkan, fungsi aktivasi yang digunakan pada lapisan tersembunyi (hidden layer) adalah fungsi logsig dan pada lapisan output menggunakan fungsi purelin. Selanjutnya, akan ditentukan banyaknya neuron yang digunakan pada proses pelatihan jaringan. Oleh karena data input yang digunakan sebanyak 2 data dan data output yang digunakan sebanyak 1 data, maka diperoleh hasil,

2√n + m = 2√2 + 1 = 2(1,412135624) + 1 ≈ 3

2n + 1 = 2(2) + 1 = 5

Oleh karena itu, banyaknya neuron yang digunakan pada lapisan tersembunyi (hidden layer) adalah dengan mencoba antara 3 sampai 5 neuron. Sehingga, diperoleh model neural network sementara adalah 2-3-1, 2-4-1, dan 2-5-1. Berikut ini merupakan nilai error untuk setiap model jaringan yang diperoleh setelah tahapan pelatihan jaringan.

Tabel 2. Nilai Error Hasil Pelatihan Jaringan

Model	Data Training			Data Testing
	MSE	MAPE	MAE	MSE	MAPE	MAE
(2-3-1)	0,0206	0,1335	0,1151	0,1139	2,3734	0,3091
(2-4-1)	0,0042	0,0626	0,0521	0,0084	0,3820	0,0713
(2-5-1)	0,0056	0,0800	0,0588	0,0470	1,4685	0,1914

Berdasarkan nilai MSE, MAPE, dan MAE yang terkecil untuk data training dan data testing adalah model 2-4-1. Model jaringan tersebut berarti bahwa terdapat 2 neuron pada lapisan input, 4 neuron pada lapisan tersembunyi (hidden layer), dan 1 neuron pada lapisan output. Bobot dan bias akhir pada lapisan input dari model jaringan feedforward neural network 2-4-1 yaitu,

Tabel 3. Bobot dan Bias Akhir pada Lapisan Input

Input Layer
Bias (βtoj}		*t-i 05ij)		yi-Sβι^}
Hidden Layer	Bobot Akhir	Hidden Layer	Bobot Akhir	Hidden Layer	Bobot Akhir
βoι	-5,6361	^ll	5,1372	β21	2,1462
β<i2	-1,9512	βl2	3,977	β22	-3,9406
βθ3	-1,8183	βl3	-4,8284	β23	-2,8721
	5,5705	βl4	5,5849	β24	0,65091

Sedangkan, bobot dan bias akhir pada lapisan output dari model jaringan feedforward neural network 2-4-1 yaitu,

Tabel 4. Bobot Akhir pada Lapisan Output

Hidden Layer	Bobot Akhir yf             I
«0	0,11124
	0,83371
a2	0,82086
«3	-1,00580
	0,19234

Dengan demikian, diperoleh model neural network yang digunakan untuk meramalkan harga penutupan saham (close price) di PT. Bank Central Asia, Tbk yaitu,

∕                     ιλ

= O,1H24+ 0,83371 -------r

∖1 + exp(-(-5,6361+ 5,1372x_t-₁ + 2,1462y_t.₁))√

∕                        1

+ 0,82086 -------₇r

∖1 + exp(-(-l,9512+ 3,977x_t.₁ - 3,9406y_t.₁))/

∕                     1

• - 1,00580 -------tr

∖1 + exp(-(-l,8183- 4,8284x_t__t - 2,8721y_t.₁))/

∕                        1

+ 0,19234 -----—-----—---------------- .(12)

∖1 + exp(-(5,5705 + 5,5849x_t.₁ + 0,65091y_f.₁))/

Berdasarkan pada persamaan tersebut terlihat bahwa model peramalan neural network untuk data penutupan saham (close price) pada periode ke t dipengaruhi oleh data harga pembukaan saham (open price) dan data harga penutupan saham (close price) pada periode ke t - 1.

• 3.3    Perbandingan Model Peramalan

Berdasarkan model fungsi transfer dan model neural network yang telah diperoleh akan dilakukan perbandingan untuk memperoleh model peramalan terbaik dalam peramalan harga penutupan saham (close price) di PT. Bank Central Asia, Tbk. Penentuan model terbaik berdasarkan nilai error yang terkecil. Berikut ini merupakan nilai error yang diperoleh dari model fungsi transfer dan model neural network.

Tabel 5. Nilai Error untuk Model Fungsi Transfer dan Neural Network

Model	MSE	MAPE	MAE
Fungsi Transfer	0,00305	0,17764	0,03972
Neural Network	0,00840	0,38200	0,07130

Berdasarkan Tabel 5 tersebut diperoleh hasil nilai MSE, MAPE, dan MAE dari model fungsi transfer lebih kecil dari model neural network. Sehingga, model terbaik yang digunakan untuk meramalkan harga penutupan saham (close price) di PT. Bank Central Asia, Tbk adalah model fungsi transfer.

Sedangkan, perbandingan hasil peramalan beserta grafiknya dari kedua model dapat dilihat pada tabel berikut ini.

Tabel 6. Perbandingan Hasil Peramalan dari Model Fungsi Transfer dan Model Neural Network

Periode Ke-	Model		Data Aktual
	Fungsi Transfer	Neural Network
91	18542	19749	18950
92	19242	20101	20300
93	20400	19957	20900
94	20196	20754	20350
95	20576	21172	21900

Time Series Plot of Data Aktual; Fungsi Transfer; Neural Network

Variable

• Data Aktual

—■— Fungsi Transfer

-÷- Neural Network

Gambar 5. Hasil peramalan untuk model fungsi transfer dan neural network

Berdasarkan Tabel 6 dan Gambar 5 terlihat bahwa pada peramalan periode ke 91, 93, dan 94 model fungsi transfer memiliki hasil peramalan yang mendekati data aktual sehingga, model fungsi transfer lebih baik digunakan daripada model neural network. Sedangkan, pada peramalan periode ke 92 dan periode ke 95 model neural network

memiliki hasil peramalan yang mendekati data aktual sehingga, model neural network lebih baik digunakan daripada model fungsi transfer.

• 4.    Kesimpulan dan Saran

Berdasarkan hasil analisis data dan pembahasan diperoleh kesimpulan bahwa model terbaik fungsi transfer adalah fungsi transfer (2,0,0)(1,0,0) dan model terbaik neural network adalah model dengan arsitektur jaringan 2-4-1. Sedangkan, model terbaik yang digunakan untuk peramalan data harga penutupan saham (close price) pada PT. Bank Central Asia, Tbk adalah model fungsi transfer. Hal ini dikarenakan nilai MSE, MAPE, dan MAE dari model fungsi transfer lebih kecil dari model neural network.

Bagi peneliti yang tertarik untuk melakukan penelitian yang sama dapat dilakukan penelitian lebih lanjut mengenai adanya pengaruh variansi yang tidak konstan atau adanya efek heterokedastisitas pada model peramalan fungsi transfer dan neural network.

Daftar Pustaka

• [1]    Samsul, Mohamad. 2015. Pasar Modal & Manajemen Portofolio Edisi 2. Surabaya: Erlangga.

• [2]    Nurini, Dwi Listya & Sutijo, Brodjol. 2013. Metode Peramalan Indeks Harga Saham Gabungan (IHSG) Nikkei 255 dengan Pendekatan Fungsi Transfer. Jurnal Sains dam Seni POMITS, Vol 2, No.2, hal 2337-3520.

• [3]    Purnama, Priska Arindya, Wardhani, Ni Wayan Surya, Fitriani, Rahma. 2017. Modelling Multi Input Transfer Function for Rainfall Forecasting in Batu City. CAUCHY-Jurnal Matematika Murni dan Aplikasi, Vol 5, No.1, p.29-35.

• [4]    Makridakis, Wheelwright & McGee. 1999. Metode Aplikasi Peramalan. Jakarta: Bina Rupa Aksara.

• [5]    Wei, William W. S. 2006. Time Series Analysis: Univariate And Multivariate Methods. California: Addison-Wesly Publishing Company.

• [6]    Elsafi, Sulafa Hag. 2014. Artificial Neural Networks (ANNs) for Flood Forecasting at Dongola Station in the River Nile, Sudan. Alexandria Engineering Journal, Vol 53, p.655-662.

• [7]    Ayodele, A., Charles, A., Marion, A. & Sunday, O. 2012. Stock Price Prediction using Neural Network with Hybridized Market Indicators. Journal of Emeging Trends in Computing and Information Sciences, Vol 3, No.1, p.1-9.

• [8]    Suyanto. 2014. Artificial Intelligence: Searching, Reasoning, Planning, dan Learning. Bandung: Informatika Bandung.

• [9]    Crone, S. F. & Kourentzes, N. 2009. Input Variable Specification for Neural Network an Analysis of Forecasting Low and High Time Series Frequency. Proceedings of International Joint Conference on Neural Network, p.619-626.

• [10]    Zhang, G. Patuwo, Edi & Hu, Michael Y. 1998. Forecasting With Artificial Neural Networks: The State Of The Art. International Journal Of Forecasting, Vol 14, p.35-62.

• [11]    Fletcher, Desmond & Goss, Ernie. 1993. Applications Forecasting with Neural Networks: An Application Using Bankruptcy Data. Information & Management, Vol 24, p.159-167.

• [12]    Fausett, L. 1994. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications. Englewood Cliffs, New Jersey: Prentice Hall.

• [13]    Zhang, G. Peter. 2003. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing, Vol 50, p.159-175.

• [14]    Ma’rufah, N., Rahayu, S. P., & Suhartono. 2013. Peramalan Pendapatan

Operasional Bank Menggunakan Metode Fungsi Transfer dan Neural Network. Jurnal Sains dan Seni POMITS, Vol 2, No.2, hal 219-224.

Berdasarkan hasil estimasi parameter tersebut, model fungsi transfer untuk meramalkan data output atau data harga penutupan saham (close price) pada PT. Bank Central Asia, Tbk dapat dituliskan dengan persamaan berikut ini.

¾(B) B(B)

^λ S_r(B)¹- *(B)“’

^ωo ,       ¹

y_t =γ¼-2

y_t = ω₀x_t-₂

ι-A(s) i ^-⅛(5) 1

^a_t

^at

y_r = 0,23672x,_, 4--a_t ^{t           t 2}  1- 0,987755 ¹

y_t(l - 0,987755) = 0,23672x_t_₂(l - 0,987755) + α_t y_t — 0,987755y_t = 0,23672x_t_₂ — 0,233820185x_t.₂ + a_t y_t — 0,98775y_t-1 = 0,23672x_t.₂ — 0,23382018x_t-3 + a_t y_t = 0,98775y_t_₁ 4- 0,23672x_t.₂ — 0,23382018x_t-3 + α_r

(H)

25