CONTROL DIFFUSION PROCESSES WITH LIPSCHITZ CONTINUITY OF DRIFTS

Jurnal Matematika Vol. 2 No. 1, Juni 2012. ISSN : 1693-1394

CONTROL DIFFUSION PROCESSES WITH LIPSCHITZ CONTINUITY OF DRIFTS

Komang Dharmawan

Jurusan Matematika FMIPA, Universitas Udayana

Kampus Bukit Jimbaran Badung, Bali e-mail: [email protected]

Abstract: Control diffusion processes has been found in a wide field of applications as in stochastic optimal control and in mathematical finance via the theory of hedging and nonlinear pricing theory for imperfect markets. In this paper we discuss the control diffusion process with time and space dependent coefficients and local Lipschitz continuity of the drift. The results show that the controlled process X_t^s,ξ,u is independent of control u for a constant.

Keywords: Stochastic Differential Equations, Lipschitz continuity, Control Diffusion Process

• 1.    Introduction

Given a bounded Borel subset U ⊂ Rⁿ, we denote by U a set of progressively measurable processes u = (u_t, t ≥ 0) defined on (Ω, F, F, P) such that P(u_t ∈ U) = 1 for all t ≥ 0. The elements of U are called admissible control processes. For each control process (u_t) ∈ U, we consider a stochastic differential equation,

{ dX^ss^ξ,u = b(t,X^s_t^ξu,ut)dt + σ(t,XS^ξu,ut)dWt,    t ≥ s,

Xs = ξ

where ∖S^ξu ∈ R^d, and b : R₊ × R^d × U → R^d, and σ : R₊ × R^d × U → R^d×ⁿ are assigned Lipschitz continuous functions for each u ∈ Rⁿ. We interpret X_t = X_t (ω) as the state of the system at time t. By a pathwise solution of this equation, we mean an (F_t)-adapted continuous stochastic process Xt'^x'^u satisfying

tt

X^ss^ξ,u = ξ +   b(r,Xs^ξu ,u_r)dr +   σ(r,Xs^ξu ,Ur)dWr,   0 ≤ s ≤ t.

(2)

ss

If the above equation has a unique solution X_t^s,ξ,u, the process (X_t) is called a controlled process.

This type of problem appears in many applications in insurance and finance. In insurance, Luo [17] consider an optimal dynamic control problem for an insurance company with opportunities of proportional reinsurance and investment. Liang [16] study optimal proportional reinsurance policy of an insurer with a risk process which is perturbed by a diffusion. The closed-form expressions for the policy and the value function are derived in the sense of maximizing the expected utility in the jump-diffusion framework.

Another papers discussing the application of control diffusion process in its application can be seen in [5], [7], [12], [13]. In financial applications, one may refer to [1], [9], [11], [14].

• 2.    Some useful facts

In this section, we review some facts which are important in next section.

Definition 2.1. A continuous function v : [0, T) × R → R is said to be upper semicontinuous if

v(s, x) ≥ limsupv(s_n, x_n) n→∞

for any s_n ∈ [0, T) and x ∈ R whenever s_n → s and x_n → x, as n → ∞.

A continuous function v : [0, T ) × R → R is said to be lower semicontinuous if

v(s, x) ≤ lim inf v(s_n, x_n) n→∞

for any s, s_n ∈ [0, T ) and x ∈ R whenever s_n → s and x_n → x as n → ∞.

The next lemma is well known.

Lemma 2.1. Let {v^α ; α ∈ A} be a family of lower semicontinuous functions. Then

v(s, x) = sup v^α(s, x) α∈A

is lower semicontinuous.

Lemma 2.2. Gronwall Lemma

Suppose that the function F : [0, T] → [0, ∞) satisfies conditions

and

where a, b ≥ 0. Then

^∫  F (t)dt < ∞

F(t) ≤ a + b

^∫ F (s)ds,

t≤T

F(t) ≤ ae^bt,   t ≤T

(3)

(4)

(5)

The proof of the Gronwall Lemma is well known, one may refer to Dharmawan [7] or Bouchard [5] for the complete proof.

The following is a standing assumption on the functions b and σ appearing in the control system.

Assumption 2.1. For each T > 0 there exists a constant K > 0 such that for all u ∈ U, s ≤ T and x,y ∈ R^d

|b(s, x, u) - b(s, y, u)| + |σ(s, x, u) - σ(s, y, u)| ≤ K|x -y|.              (6)

|b(s, x, u)| + |σ(s, x, u)| ≤ K(1 + |x|)

(7)

It is well known, see for example [11], p.158 or [22], that Assumption 2.1 yields the existence of a unique strong solution (X_t^s,ξ,u) to (1), for each s > 0, each initial condition ξ, and each u ∈ U. Moreover, (X_t^s,ξ,u) is continuous on [s, T].

Various versions of the next results are well known, see for example the monograph of Krylov [15] or Bouchard [5].

Definition 2.2. Quadratic Variation of Martingales

Let δ_n = max(tn^l₊₁ — tn) → ∞ as n → ∞. The Quadratic variation of a process (X_t) is i

defined as a limit in probability

n

(X)_t = lim £(Xtn — Xtn _ι)².                         (8)

δ→∞       ^{i      i-1}

i=1

If (Xt) is a martingale, then (X_t²) is a submartingale. By compensating X_t² by an increasing process, it is possible to make it into a martingale. The process which compensates X_t² to form a martingale turns out to be the quadratic variation of process Xt.

Theorem 2.1. If (X_t) is a local martingale, then (X,X}_t exists. Moreover Xt²-(X,X}_t is a local martingale.

Theorem 2.2. Burkholder-Davis-Gundy

For every p ≥ 1, there exist two constants c_p and C_p such that, for all continuous local martingales M vanishing at zero,

cpE [(M, M∞²] ≤ E [(M∞)^p] ≤ CpE [(M, M∞²]

where M_t^∗ = sup_s≤t |Ms|.

• 3.    Results

In this section we prove some results. The results here are not really new, but the proofs are my original works. Another version of the proofs can be seen in [5].

• Theorem 3.1.    Let ξ be an Fs-measurable random variable and for p ≥ 2 such that E|ξ|^p < ∞. Then there exists a constant K(T, p) > 0 which is independent of u such that for all 0 ≤ s ≤ t ≤ T ,

E|X_t^s,ξ,u|^p ≤ KE(1 + |ξ|^p).

(9)

Proof. We define the stopping times

inf {t ∈ [s, T]; |X_t^s,ξ,u| ≥ n}, n ≥ 1,

(10)

τn ⁼

T, if {t [s,T]; ∣X_t^s,ξ,u∣ ≥ n} = 0

The stopping times τ_n are well defined since the process X_t^s,ξ,u is continuous in t ∈ [s, T].

Then following (2) we have

t∧τn                          t∧τn

X_t^s_∧^,ξ_τ^,_n^u =ξ+       b(r, Xr^s,ξ,u, ur)dr +       σ(r, Xr^s,ξ,u, ur)dWr,   0 ≤ s ≤ t ≤ T. (11)

ss

Invoking the Burkholder-Davis-Gundy inequalities 2.2 we obtain

E|Xt∧τn|^p ≤ 3^p-1E|ξ|^p + 3^p-1E

+ ¹₂3^p-1

t∧τn

' f t∧Tn ,                       ,

∕      Ib(r,X.^,ξ,u,u_r)| dr

s'

p/2

,u_, u_r

^p

.

(12)

Using the Jensen inequality and Assumption 2.1 we find that

t∧τn

E|X_t^s_∧^,ξ_τ^,_n^u |^p ≤ 3^p-1E|ξ|^p + (3T)^p-1 K^pE         (1

p

+  ¹₂6^p-1T 2

1_E

t∧τn

(1 + |Xr^s,ξ,u|^p)dr .

s

(13)

Therefore, there exists a constant k > 0 such that

EXt∧τnIp ≤ 3^{p- 1}E∣ξ∣^p + kE ∣T (1 + ∣Xr∧UIp) dr.

(14)

(15)

The function g_n(t) = E|X_t^s_∧^,ξ_τ^,_n^u|^p is integrable on [0, T] by definition of τ_n and

gn(t) ≤ 3^p-1E|ξ|^p + k _s (1 + gn(r)) dr t ≥ s.

Therefore, by the Gronwall’s inequality (Lemma 2.2) to (15)

gn(t) ≤ (3^p-1E∣ξ∣^p + T) e^k t ∈ [s,T].

Applying the Fatou Lemma in order to pass with n → ∞ in the above inequality we conclude the proof.

• Theorem 3.2.    Let X_tⁿ be the solution of the stochastic differential equation

χs,xn,u = ξⁿ + f b(r,χs^,ξn,^u,u_r)dr + f σ(r, Xr.^,ξn,^u,u_r)dW_r,    0 ≤ s ≤ t

(16)

ss

Let (X_t) be the solution of (11) and assume that for a certain p ≥ 2

E(|ξⁿ|^p+|ξ|^p) <∞, n≥ 1.

Then there exists a constant C(p, K, T) which is independent of u such that

E sup |Xtⁿ - Xt|^p ≤ C(p,K,T)E|ξⁿ-ξ|^p. t≤T

Proof. We proceed similarly as in the proof of the previous Theorem, hence some details are omitted. Using Lipschitz property of coefficients and 2.2 we obtain

E sup |X_tⁿ - Xt|^p t≤T

≤

3p-Ieξ — ξ∣p + 3^p-Ie sup s≤t≤T

_s^t[b(r

, X_rⁿ, u_r) - b(r, X_r, u_r)] dr

^p

≤

3^{p- 1}E ∖ξ

n

_-

ξ∖^p + C1

(p, K)E  ^T

s

|b(r, X_rⁿ, u_r) - b(r, X_r, u_r)|^p dr

+ C 1(p,K,T)E T^T ∣∣σ(r,X?,u_r) s

- σ(r, X_r, u_r)∥^p dr

≤

T

3^{p- 1}E∖ξⁿ - ξ∖^p + Cι(p,κ,τ)E    ∣χn

s

- Xr|^pdr.

Now we apply the Gronwall inequality (Lemma 2.2) with gn(t) = E sup_s≤u≤t |X_tⁿ - Xt|^p to obtain

Esup ∖X_tⁿ - Xt∖^p ≤ 3^{p- 1}E ∖ξⁿ - ξ∖^p + Cι(p,K)(T - s)e^{c 11} t≤T

≤ C(p, K, T)E |ξⁿ - ξ|^p

where C(p,K,T) = max(3^{p 1} ,C ₁(p,K)(T — s)e^{c 1 t}).                             □

Theorem 3.3. Let X_t^sn,ξ,u, where 0 ≤ s_n ≤ t ≤ T be a solution of the stochastic differential equation

t∧T                          t∧T

X_t^s_∧ⁿ_T^,ξ,u =ξ+       b(r, Xr^sn,ξ,u, ur)dr +       σ(r, Xr^sn,ξ,u, ur)dWr,   sn ≤ t ≤ T (17)

s_n                                s_n

Then for all p ≥ 2 there exists a constant C(T, p) which is independent of u and such that                                             _p

E sup IXSn'^ξ'^u - χs^ξu Ip ≤ C(T,p)∖sn - s∖^p/² s≤t≤T I                        I

where s¯ = max (s, s_n).

Proof. We will prove the Theorem assuming that sn < s. The case of sn > s is completely analogous and omitted. For simplicity we assume also that the drift b = 0. Then we have

_Xtsn,ξ,u

ξ+ ^t σ(r, Xr^sn,ξ,u, ur)dWr, s_n

sn ≤ t ≤ T,

_Xts,ξ,u

ξ+ ^t σ(r, Xr^s,ξ,u, ur)dWr, s

s ≤ t ≤ T.

Let X_tⁿ = X_t^sn,x,u and X_t = X_t^s,x,u. Then for s ≤ t^′ and invoking again 2.2 we obtain

Esup ∥Xtⁿ - Xt∥^p t≤t^′

≤

C1 (T, p)E    _sn^s ∥σ(

t^′

p/2

r,Xrⁿ,ur)∥²dr     +

C1(T,p)E      ∥σ(r,Xrⁿ,ur)

s

p/2

- σ(r, X_r , u_r)∥² dr

≤

C(T,p)|sn-s|^p/2+C(T,p)E ^t ∥Xrⁿ-Xr∥^pdr.

s

Now we apply the Gronwall’s inequality (Lemma 2.2) with g(t) = E sup_s≤t≤t′ ∥X_tⁿ -Xt ∥^p . We have

E sup ∥Xtⁿ - Xt∥^p ≤ C1(T, p)|sn - s|^p/2 + C1(T, p)(sn - s)^p/2e^C1(t′-s). t≤T

Choose C(T, p) = max(C1 (T, p), C1 (T, P)e^{C1 (t′ -s)}); then

E sup ∥Xtⁿ - Xt∥^p ≤ C(T, p)|sn - s|^p/2. t≤T

Theorem 3.4. Let Assumption 2.1 hold. For each p ≥ 1, T > 0, t ≥ s2 > s1 > 0,

E sup |Xt^s2,x2,u - Xt^s1,x2,u|^p ≤ C1(|x2 - x1|^p + |s2 - s1|^p/2), s2≤t≤T

where C1, is independent of u, s, s_n, ξ.

Proof. The proof is provided for b = 0. The general case does not lead to any additonal difficulties. Let X_t¹ = X_t^s1,x1,u, X_t² = X_t^s2,x2,u. Then

E sup ∥Xt² - Xt¹∥^p s2 ≤t≤t^′

≤

3^p-1|x2 - x1|^p + 3^p-1E

s2

σ(r, X_r¹ , ur)dWr

s1

^p

+3^p-1E sup

s2≤t≤t^′

^t(σ(s,Xs²,us) s2

- σ(s, X_s¹ , us))dWs

p

Then, using the Burkholder-Davis-Gundy inequality (Theorem 2.2) we obtain

E sup ∥Xt² - Xt¹∥^p

s2 ≤t≤t^′

≤

3^p-1|x2

- x1|^p+3^p-1CpE

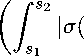
r, X_r¹ , ur

_-

)|²dr

p/2

+3^p-1CpE

t^′

|σ(s, X_s², us) s2

σ(s, X_s¹, u_s)|²ds

p/2

Using the assumptions on σ and the Jensen inequality we obtain

p s²

Esup ∣∣X2 - X^ ∣∣^p ≤ 3^p-1 ∣x2 - x 1 ∣^p + c 1 |s2 — s 112^-1      (1 + ∣X^,Us)∣p) dr

t≤T                                                                   s1

+c2T^p/2E  ^t

s2

|Xr² - Xr¹ |^p dr,

where c1, c2 > 0 are constants independent of s1, s2, x1, x2, u. Let F (t) = E sup ∥X_r² -s2 ≤r≤t

X_r¹ ∥^p. The above inequality and Theorem 3.1 yield

F(t)

≤

₃p-1

|x2

_-

x1|^p +c3|s2

_-

s1

∣^p/² + c4 ∕ F(r) dr, s2

for some positive constants c3, c4 that are independent of s1, s2, u. Moreover, if |x1 | , |x1 | ≤ R then c3 , c4 depend on R only but not on specific values of x1 and x2 . By the Gronwall inequality (Lemma 2.2) we have

F(t) ≤ 3^p-1|x2 - x1|^p + c3|s2 - s1|^p/2 + c4|s2 - s1|^p/2e^C4(t-s2).

Let C = max(3^p-1,C3,C4e^C1(t-s2)). Then

E sup ∥Xt² - Xt¹∥^p ≤ C(|x2-x1|^p+|s2-s1|^p/2).

t≤T

Theorem 3.1 - 3.4 are important to show the smoothness of value functions arising in pricing barrier options which appear in non-convex payoff functions.

References

• [1]    Avellaneda, M., Levy, A., and Paras, A. 1995. Pricing and hedging derivatives in markets with stochastic volatilities. Applied Mathematical Finance. 2, p.73-88.

• [2]    Bardi, M. and I. Capuzo Dolcetta. 1997. Optimal control and viscosity solutions to Hamilton-Jacobi-Bellman equations. Birkhauser Boston.

• [3]    Barles G. and Perthame. 1988. Exit time problems in optimal control and vanishing viscosity method. SIAM journal in Control and Optimisation. 26. p.1133-1148.

• [4]    Borkar, V.S. 1989. Optimal Control of Diffusion Processes, Pitman Research Notes, No. 203, Longman Sci. and Tech. Harlow, UK.

• [5]    Bouchard, B. 2007. Introduction to stochastic control of mixed diffusion processes, viscosity solutions and applications in finance and insurance. First Draft. Universite Paris-IX Dauphine, Ceremade and CREST

• [6]    Davis M.H.A. and J.M.C. Clark. 1994. A note on super-replicating strategies. Phil. Trans. R. Soc. London A 347, p.485-494.

• [7]    Dharmawan, K. 2005.Superreplication Method for Multi-Asset Barrier Oprions. PhD. Thesis. University of New South Wales Library. Sydney, Australis.

• [8]    El-Karoui N. and M.C. Quenez. 1995. Dynamic programming and the pricing of contingent claim in an incomplete market. SIAM, Journal of Control and Optimisation. 33. p.29-66.

• [9]    El-Karoui, S. Peng, and M.C. Quenez. 1997. Backward Stochastic Differential Equations. Mathematical Finane, Vol. 7, No. 1. p.1-71

• [10]    El-Karoui N., M. Jeanblanc-Pique, S.E. Shreve. 1998. Robustness of the Black-Schole Formula. Math. Finance 8(2), p.93-126.

• [11]    Fleming, W.H. and H.M. Soner. 1993. Controlled Markov Processes and Viscosity Solution. Springer-Verlag, New-York.

• [12]    Hipp C. and M. Plum. 2001. Optimal investment for insurers. Preprint.

• [13]    Hojgaard B. and M. Taksar. 2001. Optimal risk control for a large corporation in the presence of returns on investments. Finance and Stochastics, 5, 527-547.

• [14]    Karatzas, I. 1996. Lectures on mathematics of finance. CRM monograph series, ISSN 1065-8599; v.8

• [15]    Krylov, N.V. 1990. Control Diffusion Processes. Springer-Verlag, New York.

• [16]    Liang Z. 2007. Optimal Proportional Reinsurance for Controlled Risk Process which is Perturbed by Diffusion. Acta Mathematicae Applicatae Sinica (English Series) Volume 23, Number 3 (2007), 477-488,

• [17]    Luo S.2010. Ruin Minimization for Insurers with Borrowing onstraints. North America Actuarial Journal, Vol. 12, No. 2

• [18]    Oksendal, B. 1995. Stochastic Differential Equations. Fourth Edition, Springer Verlag, New York.

• [19]    Soner, Halil M. 1997. Controlled Markov Processes, Viscosity Solutions and Applications to mathematical Finance. in Viscosity solution and Applications. Eds. I.C. Dolcetta and P.L. Lions. p.134-185.

• [20]    Soner M. and N. Touzi. 2002. Dynamic Programming for Stochastic Target Problems and Geometric Flows. Journal of the European Mathematical Society, 4, 201236.

• [21]    Taksar M. 2000. Optimal risk/dividend distribution control models. Applications to insurance. Math. Methods Oper. Res., 1, 1-42.

• [22]    Yong J. and X.Y, Zhou. 1999. Stochastic Control : Hamiltonian Systems and HJB Equations Springer-Verlag, New York.