MODEL SIKLUS BISNIS IS-LM DENGAN PERSAMAAN DIFERENSIAL TUNDAAN
on
Jurnal Matematika Vol. 2 No. 1, Juni 2012. ISSN : 1693-1394
MODEL SIKLUS BISNIS IS-LM DENGAN PERSAMAAN DIFERENSIAL TUNDAAN
Ni Ketut Tari Tastrawati
Jurusan Matematika FMIPA, Universitas Udayana Kampus Bukit Jimbaran Badung, Bali e-mail: taritastrawati@yahoo.com
Abstract: Sistem dinamik dapat dikembangkan dalam berbagai bidang kehidupan. Seperti dalam bidang ekonomi, salah satu sistem dinamik dalam bidang ini adalah model siklus bisnis. Ada beberapa model siklus bisnis, diantaranya model IS-LM. Dalam penelitian ini akan dianalisa model siklus bisnis IS-LM dengan parameter time delay. Perbedaan antara keputusan investasi dengan implementasinya menganjurkan untuk merumuskan model siklus bisnis IS-LM yang baru, yang memperlihatkan bahwa dinamika model sangat bergantung pada parameter time delay (waktu persiapan periode investasi). Dalam penelitian ini akan digunakan teorema bifurkasi Hopf untuk memprediksi kejadian dari limit cycle untuk parameter time delay, yang menggambarkan siklus dari model IS-LM.
Keywords: bifurkasi Hopf, model IS-LM, siklus bisnis, time delay
-
1. Pendahuluan
Sistem dinamik dapat dikembangkan dalam berbagai bidang kehidupan, seperti bidang teknik, biologi, ekonomi, dan ilmu-ilmu sosial lainnya. Umumnya sistem dinamik dapat dimodelkan dalam bentuk persamaan diferensial, dan dianalisa kestabilan lokal dan global dari sistem tersebut. Salah satu model yang merupakan sistem dinamik dalam bidang ekonomi, khususnya dalam ekonomi makro adalah model siklus bisnis. Model siklus bisnis ada beberapa macam, salah satunya adalah model siklus bisnis IS-LM yang melibatkan beberapa fungsi, seperti investasi (I), saving (S), permintaan akan uang (L), dan persediaan uang (M). Model ini telah banyak dikembangkan, salah satunya oleh Torre [14] yang menganalisa keberadaan orbit tertutup dengan menggunakan teorema bifurkasi Hopf. Dari model tersebut, keputusan investasi hanya mempertimbangkan kejadian pada saat sekarang. Pada banyak aplikasi, diasumsikan suatu sistem yang menjadi perhatian, bahwa keadaan mendatang dari sistem tidak tergantung pada keadaan sebelumnya dan hanya ditentukan oleh keadaan saat ini. Apabila sistem tersebut dimodelkan dengan suatu persamaan yang menyatakan keadaan beserta percepatan perubahan keadaan tersebut, maka umumnya digunakan persamaan diferensial biasa atau persamaan diferensial parsial. Prinsip hubungan sebab akibat sering hanya merupakan suatu pendekatan awal untuk situasi sebenarnya, dan model yang lebih realistik harus meliputi keadaan sistem pada waktu sebelumnya [6]. Oleh karena itu dalam model siklus bisnis Kalecki [7], Kalecki mengasumsikan bahwa bagian yang disimpan dari keuntungan adalah investasi dan pertumbuhan modal bergantung pada keputusan investasi sebelumnya. Ini merupakan periode persiapan atau time delay. Dalam penelitian ini,
dengan menggunakan ide dari Kalecki maka Cai [1] memperumum perumusan model siklus bisnis seperti berikut:
Y = α(I (Y, K, r) - S(Y, r)) r˙ = β(L(y, r) - M¯ )
(1)
K = I(Y(t -T),K,r) -σK
dengan T adalah parameter time delay.
Investasi bergantung pada pendapatan pada waktu keputusan investasi dibuat dan juga pada stok modal pada waktu investasi berakhir. Stok modal pada waktu investasi berakhir merupakan konsekuensi dari fakta bahwa pada waktu t - T terdapat beberapa investasi yang akan berakhir antara waktu t - T dan t. Diasumsikan bahwa hasil stok modal dalam periode ini menjadi pertimbangan ketika investasi baru direncanakan. Dalam penelitian ini akan diaplikasikan teorema bifurkasi Hopf untuk memprediksi kejadian dari limit cycle untuk parameter time delay. Yang dilakukan dalam penelitian ini adalah menganalisa kestabilan linier model siklus bisnis IS-LM untuk parameter time delay yang kecil serta menyelidiki keberadaan limit cycle dari model siklus bisnis IS-LM dengan analisa bifurkasi Hopf. Dengan mengetahui keberadaan limit cycle dari parameter time delay, maka dapat ditentukan periode sistem. Dalam hal ini dinamika ekonomi makro yang salah satunya ditunjukkan dalam model siklus bisnis IS-LM mempunyai periode tertentu.
-
2. Tinjauan Pustaka
Model yang terdapat dalam [1], [9], dan [11] mengandung persamaan diferensial fungsional. Persamaan diferensial fungsional adalah suatu persamaan diferensial yang memuat ketergantungan pada masa lalu [6].
Dalam [6] diberikan tiga tipe persamaan, yaitu tipe retarded, tipe neutral dan tipe advance. Pada penerapannya, variabel bebas (sebut saja dengan t) biasanya menyatakan waktu. Persamaan tipe retarded menyatakan perilaku suatu sistem dengan laju perubahan kuantitas yang diamati tergantung pada kuantitas yang lalu atau sekarang. Tipe neutral menyajikan suatu sistem dengan laju perubahan kuantitas sekarang tergantung pada laju perubahan yang lalu dan juga kuantitas sekarang atau yang lalu. Sedangkan tipe advance menyatakan suatu sistem dengan kuantitas sekarang tergantung pada keadaan yang lalu dan laju perubahan yang lalu. Selanjutnya persamaan diferensial fungsional tipe retarded akan disebutkan dengan persamaan diferensial tundaan.
-
2.1. Kriteria Routh-Hurwitz [2, 3]
Nilai eigen dari matriks Jacobian ditentukan melalui polynomial karakteristik yang diperoleh dari persamaan |λI - A| = 0 yaitu
a0λn + a1λn-1 + a2λn-2
+ · · · + an = 0
(2)
dengan a0, a1, a2, . . . , an adalah bilangan real dan A adalah matriks Jacobian. Ser-ingkali tidak mudah menentukan akar-akar karakteristik λ1, λ2, . . . , λn, untuk itu digunakan kriteria Routh-Hurwitz yaitu:
Didefinisikan
|
D1 |
= |
a 11 |
|
D2 |
= |
a1 a3 |
|
1 a 2 | ||
|
a1 a3 a5 · · · a2k-1 | ||
|
1 a2 a4 · · · a2k-2 | ||
|
0 a1 a3 · · · a2k-3 | ||
|
Dk |
= |
0 1 a2 · · · a2k-4 . .. |
|
. .. . .. 0 0 0 ··· ak |
dengan k = 1, 2, . . . , n. Elemen aj = 0 jika j > n. Sistem dikatakan stabil jika akar-akar karakteristiknya di titik setimbang (x¯1 , x¯2, . . . , x¯n) mempunyai bagian real negatif. Akar-akar karakteristik dari (2) mempunyai bagian real negatif jika Dk > 0, untuk setiap k.
-
2.2. Bifurkasi
Dalam sistem dinamik tak linear akan sering dijumpai transisi dari keadaan stabil ke suatu keadaan tidak stabil ataupun sebaliknya yaitu transisi dari keadaan tidak stabil ke keadaan stabil. Kondisi seperti ini disebut dengan bifurkasi. Analisa bifurkasi adalah bagian terpenting dari suatu sistem. Misal diberikan medan vektor sebagai berikut:
x˙ = f (x, µ) (3)
dengan x ∈ Rn adalah variabel serta µ ∈ R adalah parameter. Sebagai konsekuensi adanya parameter dapat mempengaruhi perubahan kestabilan titik setimbang maka dikatakan strukturnya tidak stabil. Nilai parameter yang mempengaruhi sifat kualitatif sistem berubah sesuai dengan nilai bifurkasi. Dengan demikian bifurkasi dapat didefinisikan sebagai perubahan kualitatif yang terjadi pada penyelesaian persamaan diferensial. Perubahan kualitatif meliputi perubahan stabilitas dan perubahan jumlah titik setimbang yang diakibatkan perubahan parameter.
Untuk menganalisis bifurkasi dari medan vektor dapat digunakan bidang parameter, sehingga didapatkan berbagai jenis bifurkasi seperti bifurkasi Hopf, bifurkasi sadel node, dan yang lainnya.
-
2.3. Bifurkasi Hopf
Pandang sistem persamaan diferensial
x˙ = f (x, y, µ) y˙ = g(x, y, µ)
(4)
dengan parameter µ. Diasumsikan sistem (4) mempunyai titik setimbang (x0, y0) dan µ = µ0 adalah nilai parameter yang menyebabkan terjadinya bifurkasi. Bifurkasi Hopf terjadi jika titik setimbang x0 , y0 mempunyai sepasang nilai eigen kompleks yaitu λ(µ0) = α(µ0) + iω(µ0) dan λ(µ0) = α(µ0) - iω(µ0) dengan α(µ0) = 0, ω(µ0) ̸= 0 dan memenuhi syarat transversal [5].
-
3. Hasil dan Pembahasan
-
3.1. Model IS-LM
-
Diasumsikan bahwa fungsi Investasi I , fungsi Saving S , dan permintaan akan uang L bergantung secara linear pada argumen-argumennya. Suku bunga r mempunyai hubungan yang berbanding terbalik dengan investasi sehingga semakin tinggi tingkat suku bunga maka investasi semakin turun. Stok modal mengalami penyusutan nilai sebesar δ , sehingga fungsi investasi (I ) dapat dinyatakan sebagai besarnya pendapatan (dalam hal ini gross product) dikurangi modal dan suku bunga. Saving atau simpanan merupakan besarnya pendapatan ditambah suku bunga. Sedangkan pemintaan uang di pasar berbanding terbalik dengan suku bunga, semakin tinggi tingkat suku bunga semakin turun permintaan akan uang di pasar, sehingga fungsi permintaan akan uang (L) dapat dinyatakan sebagai besarnya pendapatan (gross product) dikurangi besarnya suku bunga. Secara singkat dapat dinyatakan sebagai berikut:
dengan η, δ1 , l1 , l2, β1 , β2, β3 adalah konstanta-konstanta positif dalam interval [0, 1].
-
3.2. Persamaan Karakteristik Model IS-LM
Berdasarkan persamaan (5), (6), dan (7), maka sistem (1) dapat dibentuk menjadi
Y = α((η - l1)Y - (β1 + β2)r - δ1K)
r˙ = β(l2Y -β3r-M) (8)
K = ηY(t-T) -β1r - (δ + δ1)K
Titik setimbang sistem (8), diperoleh dengan membentuk Y = 0, r˙ = 0, K = 0, serta T = 0, sehingga didapatkan titik setimbang trivial S0(0, 0, 0), sedangkan titik setimbang nontrivialnya adalah S1 = (Y , r¯, K), dengan
(δβ2 +δ1β2 + δβ1)M
Y =-
-
-β3l1δ1 - β3l1δ - β1l2δ + β3ηδ - β2l2δ1 - β2l2δ
¯ (-l1δ1 - l1δ + ηδ)M
-
r = --β3l1δ1 - β3l1δ - β1l2δ + β3ηδ - β2l2δ1 - β2l2δ
(l1β1 + ηβ2)M
K=-
-
-β3l1δ1 - β3l1δ - β1l2δ + β3ηδ - β2l2δ1 - β2l2δ
Selanjutnya akan dicari persamaan karakteristik dari sistem (8). Persamaan karakteristik dibentuk melalui:
|
α(η - l1) - λ |
-α(β1 + β2) |
-αδ1 | |
|
βl2 |
-ββ3 - λ |
0 |
= 0 |
|
ηe-λT |
-β1 |
-(δ + δ1 ) - λ |
sehingga persamaan karakteristik dari persamaan (8) berbentuk:
λ3 + Aλ2 + Bλ + C + Dλe-λT + Ee-λT = 0 (9)
dengan
A = δ + δ1 + ββ3 - α(η - l1)
B = (δ + δ1)(ββ3 - α(η - l1)) + αβl2(β1β2) - αββ3 (η - l1)
C = -αββ1l2δ1 - (δ + δ1)αβ(β3(η - l1) - l2 (β1 + β2))
D = αηδ1
E = αββ3ηδ1
Persamaan transendental (9) tidak dapat diselesaikan secara eksak sehingga mempunyai banyak akar. Untuk itu perlu dilakukan pendekatan lain yaitu dengan pendekatan linear dan pendekatan dalam ruang kompleks.
3.3. Pendekatan Linear
Untuk time delay T yang kecil, pendekatan linear sangat cocok untuk memperoleh titik bifurkasi. Untuk T yang sangat kecil maka
e
-λT
1-
λT
, sehingga persamaan (9) menjadi
λ3+(A-DT)λ2+(B+D-ET)λ+C+E=0(10)
Dengan teorema bifurkasi Hopf dan kriteria Routh-Hurwitz, maka terjadi bifurkasi Hopf pada nilai T = T0 dengan
ADT0 > 0, B + D - ET0 > 0, C + E > 0(11)
dan
(A - DT0)(B + D - ET0) = C+E(12)
Misalkan
g(λ,T) =λ3+(A-DT)λ2+(B+D-ET)λ+C+E=0
maka dapat ditentukan g pada T = T0
g(λ,T) = λ3+sλ2+k2λ+k2s
dengan
s= (ADT0), k2 = (B+D-ET0)
Nilai eigen dari persamaan (10) diperoleh sebagai berikut:
λ0(T0) = -s = -(A - DT0)
λ1,2(T0) = ±ik = ±i(B + D -ET0)12
Selanjutnya, akan ditunjukkan bahwa syarat transversal terpenuhi, yaitu
Re (d(λ(T^=T0) =0
Diferensiasi total g(λ(T), T) menghasilkan
∂g
dλ = - ∂T
dT = ∂g
∂λ
-
-Dλ2 - Eλ
-
3λ2+2(A-DT)λ+B+D-ET
Dihitung turunan g untuk λ = λ1 pada saat T0 , diperoleh
d ,. . (Dk2 - iEk)(-3k2 + B + D - ETo - i2k(A - DT0))
(13)
dT (λ1(T)) = - P2+R2
T =T0
dengan
P = -3k2 + B + D - ET0
R = 2k(A - DT0)
Bagian real dari (13) adalah
Re ddT (λ1(T))
=
T=T0
Dk2(-3k2 + B + D - ET0) - 2Ek2(A - DT0) P2+R2
Ada dua kemungkinan yang terjadi, yaitu:
-
1. Kemungkinan pertama
Re (d(λ 1(T))|T=T0) > 0
Dk2(-3k2 + B +D - ET0) - 2Ek2 (A - DT0)
-
- P2+R2 >0
karena P2 + R2 pasti positif, maka haruslah
-Dk2 < E(A- DT0)
-D(B + D - ET0) < E(ADT0)
(14)
Perhatikan bahwa untuk D dan E positif, pertidaksamaan (14) terpenuhi jika kondisi (ADT0) > 0 dan (B + D - ET0) > 0 terpenuhi
2. Re ddT (λ1(T))
<0
T=T0
Dengan cara yang sama seperti kemungkinan pertama, ternyata kemungkinan yang kedua tidak sesuai dengan kriteria Routh-Hurwitz, sehingga yang memenuhi
adalah kemungkinan pertama yaitu Re ddT (λ1(T))
> 0 , dan dapat dis-
impulkan bahwa Re (ddT(λ1(T))
T=T0
̸= 0 . Menurut teorema bifurkasi Hopf,
hal ini menjamin adanya limit cycle pada saat T = T0
-
3.4. Pendekatan Dalam Ruang Kompleks (Analisa Bifurkasi Hopf)
Untuk time delay yang lebih panjang, pendekatan linear tidak efektif lagi digunakan, sehingga diperlukan pendekatan yang lain. Dengan mengambil λ = σ + iω , persamaan (9) dapat ditulis dalam bentuk bagian real dan bagian imajiner.
(σ3 - 3σω + Aσ2 + Bσ + C + eσT (Dω cos ωT + Dω sin ωT + E cos ωT))+ i(3σ2ω - ω2 + 2Aσω + Bω + e-σT (Dω cos ωT - Dσ sin ωT - EsinωT)) = 0 (15)
Sehingga bagian real persamaan (15) berbentuk
σ3 - 3σω + Aσ2 - Aω2 + Bσ + C + e-σT (Dσ cos ωT + Dω sin ωT + EcosωT) = 0
Sedangkan bagian imajinernya adalah
3σ2ω - ω2 + 2Aσω + Bω + e-σT (Dω cos ωT - Dσ sin ωT - EsinωT) = 0
Untuk mendapatkan titik bifurkasi yang pertama, diambil σ = 0. Sehingga bagian real
dan bagian imajiner diatas direduksi menjadi
Kemudian kedua persamaan (16) dan (17) dibentuk menjadi
Dengan menguadratkan persamaan (18) dan (19), kemudian menjumlahkannya akan menghasilkan
ω6+ (A2 - 2B)ω4 + (B2 - 2AC - D2)ω2 +C2 -E2 = 0(20)
Jika titik bifurkasi pertama adalah ωbif, Tbif, maka titik bifurkasi yang lain ω, T harus memenuhi
ωT = ωbifTbif + 2nπ, n = 1, 2, · · ·
Persamaan (20) merupakan persamaan kubik dalam ω2 dan sisi kiri dari persamaan ini bernilai positif untuk nilai ω2 yang besar dan akan bernilai negatif untuk ω = 0 dan C2 < E2 . Oleh karena itu, jika kondisi diatas terpenuhi, maka persamaan (20) mempunyai paling sedikit satu akar real positif.
Lemma 3.1. Syarat perlu dan cukup bahwa persamaan kubik
z + a1z + a2z + a3 = 0
dengan a3 > 0, mempunyai paling sedikit satu akar positif adalah:
-
1. berlaku salah satu dari
-
a. a1 < 0, a2 ≥ 0 dan a21 > 3a2 atau
-
b. a2 < 0
-
2. ∆ < 0, dengan ∆ = a32 - a21a22 + a31a3 - a1a2a3 + a33
27 27 27 3
Untuk membuktikan terjadi bifurkasi Hopf pada T = Tbif, maka perlu ditunjukkan
bahwa
Re d (λ(T)) dT
̸= 0
T=Tbif
Misalkan G(λ(T), T) = λ3+Aλ2+Bλ+C+DλeλT +Ee-λT , maka diferensiasi G(λ(T), T) menghasilkan
∂G
dλ ∂T
dT = ∂G
∂λ
(Dλ2 + Eλ)e-λT
(21)
= 3λ2+2Aλ+B+ (D-Tλ-ET)e-λT
Dihitung turunan G pada saat T = Tbif dan λ = iωbif
dT (λ(T)) = [(-Dωbif cos ωbifTbif + Eωbif sin ωbifTbif) + i(Dωbif sin ωbifTbif
+ Eωbif cos ωbifTbif)] · [(-3ωb2 if + B + D cos ωbifTbif
-
- DωbifTbif sin ωbifTbif - ETbif cos ωbifTbif) - i(2Aωbif
-
- D sin ωbifTbif - DωbifTbif cos ωbifTbif + ETbif sin ωbifTbif)]/ [(-3ωbifTbif + B + D cos ωbifTbif - DωbifTbif sin ωbifTbif
-
- ETbif cos ωbifTbif) + i(2Aωbif - D sin ωbifTbif - DωbifTbif cos ωbifTbif
+ ETbif sin ωbifTbif)] · [(-3ωb2 if + B + D cos ωbifTbif
-
- DωbifTbif sin ωbifTbif - ETbif cos ωbifTbif) - i(2Aωbif
-
- D sin ωbifTbif - DωbifTbif cos ωbifTbif + ETbif sin ωbifTbif)]
sehingga bagian real dari persamaan (21) pada saat T = Tbif dan λ = iωbif, adalah
RE ddT (λ(T)) =
ω2 (3ω4 + 2ω2 (A2 - 2B) + B2 - 2AC - D2) bif bif bif
P12 + Q21
dengan
P1 = -3ωb2 if + B + Tbif(-Aωb2 if + C) + D cos ωbifTbif
Q1 = 2Aωbif + Tbif(-ωb3if + Bωbif) - D sin ωbifTbif
Misalkan x = ωb2if , maka persamaan (20) menjadi
f(x) =x3+(A2-2B)x2+(B2-2AC-D2)x+C2-E2
dan
f′(x) =3x2+2(A2-2B)x+(B2-2AC-D2)
Jika ωbif adalah akar positif terkecil dari persamaan (20) (kecuali jika merupakan akar kembar maka dipilih akar terkecil berikutnya), maka
oleh karena itu
f′(x)
>0 T=Tbif
dσ
dT T=Tbif
ω2 f′(ω2 ) bif bif
P12 + Q21
>0
yang memperlihatkan bahwa syarat transversal terpenuhi, sehingga terbukti terjadi bi-furkasi Hopf pada saat T = Tbif .
Dari analisa bifurkasi Hopf diatas, jika Lemma 3.1 terpenuhi dan ωbif adalah akar positif terkecil dari persamaan (20) (kecuali jika merupakan akar kembar maka dipilih akar terkecil berikutnya), maka bifurkasi Hopf terjadi pada saat T melewati Tbif .
Contoh Jika
α = 3, β = 2, σ = 0.1, σ1 = 0.5, η = 0.31, l1 = 0.2, l2 = 0.1
M = 0.05, β1 = β2 = 0.2
maka sistem (1) menjadi
Y = 0.3Y - 1.2r - 1.5K
r˙ = 0.2Y - 0.4r - 0.1 (22)
K = 0.3Y(t-T) - 0.2r - 0.6K
Persamaan karakteristik (22) akan berbentuk:
λ3 + 0.7λ2 + 0.18λ + 0.012 + 0.45λλT =0
Jika Lemma 3.1 terpenuhi dan ωbif adalah akar positif terkecil dari persamaan (20) (kecuali jika merupakan akar kembar maka dipilih akar terkecil berikutnya), maka bifurkasi Hopf terjadi pada saat T melewati Tbif = 0.740471, dengan nilai eigen
λ0(Tbif) = -0.382583 λ1,2 (Tbif) = ±0.6993i
Oleh karena itu periode dari limit cycle adalah
2π
2π
T = = = 8.98496
|λ(Tbif)| 0.6993
yang menggambarkan bahwa periode dari sistem ekonomi (dalam hal ini model IS-LM) adalah sekitar 9.
Berikut ini hasil plotting time series dari Contoh:

Gambar 1. Grafik kestabilan Model IS-LM pada Tbif = 0.740471, dengan history [0.5; 0.015; 1.25]
Untuk T diluar Tbif = 0.740471, grafiknya sebagai berikut:

Gambar 2. Grafik kestabilan Model IS-LM pada T = 0.4, dengan history [0.5; 0.015; 1.25]

Gambar 3. Grafik kestabilan Model IS-LM pada T = 1, dengan history [0.5; 0.015; 1.25]
Gambar 1. menunjukkan terjadi limit cycle pada = 0.740471, hal ini menggambarkan periode dari model IS-LM sekitar 9. Gambar 2. menunjukkan struktur orbit di dalam limit cycle akan menjauhi limit cycle ( terlihat bahwa osilasinya teredam), sedangkan Gambar 3 menunjukkan struktur orbit di luar limit cycle akan menjauhi limit cycle (osilasinya semakin membesar). Secara sederhana dapat digambarkan bahwa limit cycle-nya tidak stabil (Gambar 4.).
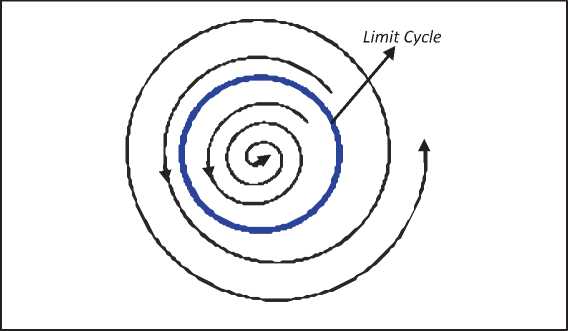
Gambar 4. Ilustrasi sederhana dari limit cycle yang tidak stabil
Lingkaran biru menunjukkan limit cycle dari model IS-LM (Gambar 1), sedangkan orbit spiral di dalam limit cycle menunjukkan Gambar 2 dan orbit spiral di luar limit cycle menunjukkan Gambar 3. Sehingga dapat dikatakan bahwa bifurkasi Hopf yang terjadi dalam Contoh merupakan bifurkasi Hopf Subkritikal (tidak stabil).
-
4. Kesimpulan dan Saran
-
4.1. Kesimpulan
-
Kesimpulan yang diperoleh dari analisa dan aplikasi bifurkasi Hopf pada model siklus bisnis IS-LM adalah
-
1. Dari model diperoleh persamaan karakteristik yang tidak dapat diselesaikan secara eksak, sehingga perlu pendekatan lain yaitu pendekatan linear dan pendekatan dalam ruang kompleks (analisa bifurkasi Hopf).
-
2. Dengan pendekatan linear diperoleh tiga nilai eigen dengan sepasang nilai eigen kompleks yang bagian realnya nol atau ima jiner murni yang merupakan syarat terjadinya bifurkasi Hopf. Dan dengan terpenuhinya syarat transversal yaitu
Re (dT(λ ■ t ))∣τ=t0)=0 ■
maka bifurkasi Hopf terjadi pada nilai T = T3 yang menjamin adanya limit cycle pada nilai ini.
-
3. Pada pendekatan dalam ruang kompleks (analisa bifurkasi Hopf), bifurkasi Hopf terjadi pada saat T melewati Tbif .
-
4.2. Saran
Untuk penelitian selanjutnya dapat dianalisa di bidang mana letak dari limit cycle yaitu dengan analisa center manifold.
Daftar Pustaka
-
[1] Cai, J. (2005). Hopf Bifurcation in The IS-LM Business Cycle Model with Time Delay. Electronic Journal of Differential Equations. 15. 1-6.
-
[2] Cronin, J., (1994). Differential Equations: Introduction and Qualitative Theory. Second Edition. Marcel Dekker,Inc. NewYork.
-
[3] Deo, S.G., Raghavendra,V. (1980). Ordinary Differential Equations and Stability Theory. Tata McGraw-Hill. New Delhi.
-
[4] Golubitsky,M.,Dellnitz,M. (1998). Linear Algebra and Differential Equations Using Matlab. Brooks/Cole Publishing Company. California.
-
[5] Guckenheimer, J. dan Holmes, P.(1990). Nonlinear Oscilations Dynamical System and Bifurcation of Vector Fields. Springer-Verlag. New York.
-
[6] Hale, J.K.,Lunel,S.M.V. (1993).Introduction to Functional Differential Equations. Springer-Verlag New York,Inc
-
[7] Kalecki,M.(1935). A Macrodynamic Theory of Business Cycle. Econometrica. 3. 327-344.
-
[8] Khan,Q.J.A. (2000).Hopf Bifurcation in Multiparty Political Systems with Time Delay in Switching. Applied Matematics Letters. 13. 43-52.
-
[9] Krawiec,A. Szydlowski,M. (2001).The Kaldor-Kalecki Model of Business Cycle as A Two-dimensional Dynamical System. Journal of Nonlinear Mathematical Physics. 8. 266-271.
-
[10] Kuang, Y. (1993).Delay Diferential Equations with Applications in Population Dynamics. Academic Press, Inc. New York.
-
[11] Neamtu,M., Opris,D., Chilarescu,C. (2005). Hopf Bifurcation in A Dynamic IS-LM Model with Time Delay. arXiv:math.DS/0511322. 1. 1-13
-
[12] Perko,L. (1998). Differential Equations and Dynamical Systems. Second Edition. Springer-Verlag New York,Inc
-
[13] Subiono. (2003).Matematika Sistem. Jurusan Matematika FMIPA ITS. Surabaya.
-
[14] Torre,V. (1977).Existence of Limit Cycle and Control in Complete Keynesian Systems by Theory of Bifurcation. Econometrica. 45. 1457-1466.
-
[15] Wiggins,S.(1990). Introduction to Applied Non Linear Dynamical Systems and Chaos. Second Edition. Springer - Verlag. New York
Discussion and feedback