FRAKTAL DAN INVERS FRAKTAL
on
Jurnal Matematika Vol. 2 No. 1, Desember 2011. ISSN : 1693-1394
FRAKTAL DAN INVERS FRAKTAL
Beni Utomo
Laboratorium Matematika Komputasi
Jurusan Informatika, Sekolah Tinggi Teknologi Bontang
Abstract: Fraktal sebagai sebuah geometri bisa digambarkan pada ruang dimensi dua dengan syarat yang harus dipenuhi yaitu bisa didefinisikan pada ruang metrik lengkap. Untuk mengkonstruksi fraktal secara geometri tersebut diperlukan suatu himpunan fungsi yang dikenal dengan nama IFS dan jika IFS tersebut diiterasikan maka akan terbentuk suatu citra yang dikenal sebagai citra fraktal, artinya setiap ada IFS maka selalu bisa dikonstruksi citra frak-tal. Invers fraktal merupakan balikan dari proses tersebut, yaitu jika diberikan sebarang citra fraktal maka bisakah ditemukan IFSnya. Jaminan adanya IFS tersebut dikenal dengan nama Teorema Collage.
Keywords: ruang fraktal, fraktal, IFS, invers, teorema collage.
Konstruksi geometri fraktal secara matematis antara lain terdapat dalam buku Barnsley [1] yang secara singkat bisa diuraikan sebagai berikut. Diberikan ruang metrik kompak (X, d) dan didefinisikan H(X) = {A C X\A kompak atauA =}. Didefinisikan fungsi h : H(X) × H(X) —→ R + dengan h(A, B) = Maks(d(A, B),d(B, A)) dan d(A, B) = maks{Min{d(x,y) : y ∈ B} : x ∈ A} untuk setiap A, B ∈ H(X). Fungsi h merupakan metrik yang disebut metrik Hausdorff dan (H(X), h) merupakan ruang metrik lengkap dan sering disebut ruang fraktal.
Sistem Fungsi Iterasi atau Iterated Function System (IFS) didefinisikan sebagai suatu sistem yang terdiri dari ruang metrik lengkap (X, d) dan pemetaan-pemetaan kontraksi wn : X —→ X dengan faktor kontraksi Sn, 0 < sn < 1 untuk n = 1, 2, 3, . . . , N . Dalam hal ini IFS diberi notasi {X; w i ,w 2,..., wn} dengan faktor kontraksi s = Maks {sn : n = 1, 2, 3,..., N} . Akibatnya terdapat n
dengan tunggal titik tetap A ∈ H(X) dengan A = W(A) = wn An (A) sehingga A dapat dicari n=1
secara iteratif oleh A = limn→∞ Wn(B) untuk setiap B ∈ H(X). Titik tetap ini disebut atraktor (attractor) IFS. Untuk X = R2 , maka sudah ditemukan 3 algoritma untuk mencari atraktor tersebut, yaitu algoritma deterministik, algoritma iterasi random, dan algoritma cat game atau chaos game (Widodo [20]). Pada saat mengkonstruksi geometri fraktal, terlebih dahulu dimiliki IFS, dan jika IFS tersebut diiterasikan maka akan terbentuk suatu citra geometri yang disebut citra fraktal. Dengan bantuan komputer grafik, atraktor dapat digambarkan dengan baik dan ternyata memberikan keindahan fraktal yang sangat menakjubkan seperti bentuk Fern, Segitiga Sierpinski, Sponge dan sebagainya. Akibatnya bisa dikatakan bahwa jika dimiliki sebarang IFS maka citra fraktal bisa dibentuk. Pertanyaan selanjutnya adalah bagaimana jika kejadian tersebut dibalik. Jika dimiliki sebarang citra awal, apakah mungkin ditemukan suatu IFS yang jika IFS tersebut diiterasikan akan membentuk suatu citra fraktal, dengan sifat citra fraktal tersebut mirip dengan citra awal. Teorema Collage (Barnsley [1]) menjamin bahwa IFS dengan sifat demikian mungkin untuk dibentuk.
Teori dasar yang digunakan makalah ini adalah ruang metrik dan fraktal. Ruang metrik memberikan dasar konstruksi fraktal yang dikonstruksi melalui proses iteratif.
Definisi 1.1. Diberikan ruang metrik (X, d) dan transformasi f : X -→ X . Iterasi maju dari f merupakan transformasi f °n (x) = x dengan fo0(x) = x, fo0(x) = f (x), f o(n +1)(x) = f ◦ f °n (x) = f (fon (x)) untuk n = 0, 1, 2, ∙∙∙ Jika f invertibel maka bisa didefinisikan iterasi mundur f yaitu fo(-m)(x) : X —→ X dengan fo(-1)(x) = f-1(x), f o(-m)(x) = (fom)-1(x) untuk m = 1,2, 3, ∙ ∙.
Definisi 1.2. Pemetaan Kontraksi (Barnsley [1]). Suatu transformasi f : X -→ X pada ruang metrik (X, d) disebut transformasi kontraktif atau pemetaan kontraksi jika terdapat suatu konstanta s, dengan 0 ≤ s < 1 sehingga berlaku d(f (x), f(y)) ≤ (s) · d(x, y) untuk setiap x, y ∈ X.
IFS mengkonstruksi fraktal dengan cara mengulang transformasi berkali-kali untuk sebarang pola awal. Pola awal ditransformasi menjadi suatu pola berulang dengan struktur yang sama pada detail tertentu, hal tersebut merupakan karakteristik dasar dari himpunan fraktal.
Teori transformasi fraktal merupakan teori IFS lokal. Meskipun IFS lokal merupakan teori yang cukup rumit untuk menemukan fraktal, namun pada kenyataannya IFS lokal bisa menyederhanakan proses. Suatu transformasi global pada ruang X merupakan suatu transformasi yang didefinisikan untuk semua titik anggota X ; sementara transformasi lokal merupakan transformasi dengan domainnya adalah himpunan bagian dari X dan transformasi tersebut tidak perlu dikenakan pada semua anggota X , sehingga pengertian IFS lokal merupakan IFS yang dikenakan tidak pada semua domain tetapi hanya dikenakan pada domain yang merupakan himpunan bagian dari ruang yang dipakai.
Ide menemukan fraktal seperti disebutkan sebelumnya adalah menemukan ruang bagian dari ruang fraktal yang bisa diperbaharui menggunakan IFS. Jika mungkin, satu IFS dapat digunakan untuk menggantikan beberapa IFS untuk membuat fraktal yang sama, hal tersebut lebih efisien dan hemat karena jumlah anggota IFS yang lebih kecil. Hal tersebut mirip dengan pernyataan bahwa suatu citra fraktal memerlukan lebih dari satu IFS untuk memproduksinya supaya mirip dengan citra aslinya.
Definisi 1.3. Pemetaan Kontraksi Lokal (Soberano [17]) Diberikan (X, d) ruang metrik kompak dan S ⊂ X dengan S ̸=. Pemetaan w : S -→ X dikatakan kontraksi lokal pada (X, d) jika terdapat bilangan real s dengan 0 ≤ s < 1 sehingga d(w(x), w(y)) ≤ (s)(d(x, y)) untuk setiap x, y ∈ S.
Definisi 1.4. IFS Lokal (Soberano [17]) Pemetaan wi : Si -→ X pemetaan kontraksi lokal pada
N
ruang metrik (X, d) dengan faktor kontraksi si untuk i =
1, 2, . . . , N dan Si = S . Selanjutnya
i-1
{S : wi : Si -→ X, i = 1, 2, . . . , N } disebut IFS lokal.
Bilangan s = maks{si : i = 1, 2, . . . , N} disebut faktor kontraksi untuk IFS lokal. IFS lokal juga
bisa dinyatakan sebagai berikut. Jika G menyatakan himpunan semua subset dari X , maka bisa N
didefinisikan suatu operator wlokal : G —→
G dengan wlokal(B) = ∣Jwi (Si ∩ B) untuk semua B ∈ G
i=1
Dengan batasan tersebut, wιokaι dapat didefinisikan sebagai pemetaan kontraksi pada himpunan
bagian dari ruang Hausdorff. Jika A adalah himpunan bagian tak kosong dari X , himpunan A disebut atraktor dari IFS lokal jika wlokal(A) = A. Jika himpunan A dan B adalah atraktor maka A ∪ B juga atraktor. Jika terdapat suatu atraktor, terdapat atraktor terbesar yang memuat semua atraktor yang lain tersebut. Atraktor terbesar ini berkenaan dengan atraktor dari wlokal dan ditemukan dengan mengambil gabungan dari semua atraktor lain dalam wlokal .
Diberikan IFS Lokal {S; wi : Si -→ X, i = 1, 2, . . . , N} dan misalkan himpunan Si kompak maka dapat didefinisikan suatu barisan himpunan kompak bagian dari X dengan:
A0 = X
N
An = wi(Si ∩ An-1)
i=1
untuk n = 1, 2, . . . , N
Karena IFS memuat pemetaan-pemetaan kontraksi maka
A0 ⊂ A1 ⊂ A2 ⊂ A3 ⊂ · · ·
sehingga {An} merupakan barisan himpunan kompak yang menurun. Akibatnya ada suatu himpunan kompak A ⊂ X dengan sifat
lim An = A n→∞
dan
N
A = ∪ Wi (Si ∩ A) = w lokal (A)
i=1
Telah disyaratkan sebelumnya, jika A tak kosong maka merupakan atraktor maksimal untuk IFS lokal. Jika ada himpunan kompak B sehingga wlokal(B) ⊂ B maka kemungkinan bahwa A adalah kosong. Himpunan A berkaitan dengan atraktor suatu IFS pada pola penentuan citra fraktal. Koefisien dari pemetaan wi cukup penting dalam penetapan citra fraktal tersebut.
Konstruksi fraktal dimulai dengan dimilikinya suatu IFS yang diiterasikan akan menghasilkan citra fraktal. Bagaimana dengan proses sebaliknya? Jika dimiliki suatu fraktal, bisakah selalu ditemukan suatu IFSnya? Barnsley memberikan jawaban untuk masalah tersebut melalui teorema collage.
Teorema 1.1. Teorema Collage ( Barnsley [1]) Diberikan (X, d) ruang metrik lengkap dan T ∈ H(X). Untuk sebarang bilangan ε > 0, diambil suatu IFS {X; (w0), w1, w2, . . . , wN} dengan faktor kontraksi 0 ≤ s < 1 sehingga
h
(T,∪1 wn (T)j ≤ ε
dengan h(d) adalah metrik Hausdorff, maka
h(T,A) ≤
ε
1-s
dengan A adalah atraktor dari IFS, ekuivalen dengan mengatakan h(T, A) ≤ (1-s)-1h untuk semua T ∈ H(X)
[ T, IJ Wn (T J
Teorema Collage menjamin adanya IFS yang hasil iterasinya merupakan suatu fraktal yang mirip dengan sebarang himpunan bagian kompak yang diberikan. Secara singkat teorema collage bisa dikatakan sebagai berikut. Jika diberikan sebarang T ∈ H(x) maka bisa dicari suatu IFS, dan jika IFS tersebut diiterasikan sebanyak N kali, maka akan ditemukan suatu himpunan kompak lain yaitu NN
|J wn(T) dengan sifat bahwa T ∈ H(X) dan J wn(T) sangat mirip. Sedangkan himpunan A yang n=1 n=1
N
memenuhi A = W(A) =I I wn (A) merupakan atraktor dari IFS yaitu A = lim Won (B) untuk setiap n→∞
n=1
B ∈ H(X). Ada hal yang berbeda mengenai arti invers dari fraktal dengan pengerttian invers secara umum. Jika invers secara umum menghasilkan sesuatu yang adalah sama sebelum ketika sesuatu tersebut dikenakan fungsi tetapi tidak demikian dengan invers fraktal. Invers fraktal menghasilkan suatu himpunan kompak yang mirip dengan himpunan awal sebelum dicari IFS nya.
Salah satu aplikasi dari invers fraktal yang dikonstruksi melalui teorema collage adalah citra fraktal yang mirip dengan sebarang citra asli yang diberikan. Pandang himpunan R2. Diambil sebarang S C R2 dengan S himpunan bagian kompak. Dipihak lain, jika diambil sebarang citra nyata berukuran n x m dengan n, m ∈ R maka citra tersebut merupakan himpunan kompak. Dengan kata lain jika diambil sebarang S C R2 dengan S himpunan kompak maka himpunan S bisa dipandang sebagai citra nyata.
Dengan demikian Teorema Collage di R2 bisa dipandang sebagai berikut. Diberikan ruang metrik lengkap (R2, d) dengan d adalah metrik biasa, dan sebarang citra nyata T ∈ H(R2). Untuk sebarang bilangan ε > 0 , bisa ditemukan suatu IFS {X; (w0),w 1 ,w2,... ,wn} dengan faktor kontraksi 0 ≤ s < 1 sehingga citra hasil iterasi dari IFS menjadi mirip dengan citra nyata T .
Pada perkembangannya IFS masih bisa bekerja jika transformasi affine kontraksi dibatasi hanya bekerja pada bagian-bagian dari keseluruhan citra. Ide pengganti untuk menemukan transformasi affin yang memetakan keseluruhan citra menjadi bagian-bagian dari citra itu sendiri adalah mencari suatu transformasi affine yang memetakan bagian citra ke bagian citra yang lain.
Metode yang dipakai untuk mengkonstruksi citra fraktal adalah metode pencocokan bagian-bagian citra (matching) antara bagian citra asli dengan citra yang nantinya akan dikonstruksi menjadi citra fraktal yang mirip dengan citra asli. Awalnya citra asli dan citra awal dibagi menjadi potongan-potongan citra. Selanjutnya potongan-potongan tersebut dilakukan pencocokan dengan menggunakan transformasi affine. Akibatnya transformasi affine yang diperlukan lebih dari satu dan menjadi himpunan transformasi affine. Pencocokan yang sedemikian rupa, yang terjadi antar potongan-potongan citra menjadikan himpunan transformasi affine tersebut tidak lagi IFS tetapi menjadi Partitioned Iterated Function System atau PIFS.
Dalam penelitian ini digunakan tiga bahan utama untuk penelitian yaitu buku referensi dan jurnal, citra, dan program komputasi. Buku dan jurnal dipakai untuk memberikan dasar dan kajian teoritis serta contoh-contoh untuk membuat desain program. Citra yang dipilih adalah citra skala abu-abu dan bahasa pemrograman yang dipilih adalah MATLAB. Program yang dibangun terdiri dari dua bagian, bagian pertama program berfungsi untuk encoding atau pengkodean citra sedangkan bagian kedua berfungsi untuk decoding atau pembuatan citra fraktal.
Percobaan-percobaan meliputi beberapa tahapan. Tahapan pertama merupakan percobaan untuk mengetahui pengaruh transformasi yang dikenakan pada citra, meliputi dilatasi, rotasi, pen-
skalaan, dan transformasi miring. Tahapan kedua merupakan percobaan untuk menyusun citra frak-tal berdasarkan citra Lena. Percobaan dilakukan dengan partisi ukuran pixel yang berbeda-beda dan selanjutnya hasil yang diperoleh akan dibandingkan.
Ada dua proses inti yang dilakukan untuk menyelesaikan permasalahan yaitu proses menemukan IFS yang disebut encoding dan proses mengiterasikan IFS untuk membentuk fraktal yang disebut decoding. Untuk menyelesaikan proses tersebut secara manual tidaklah mungkin, karena selain melibatkan sejumlah besar potongan citra juga ukuran citra yang sangat kecil sehingga dengan keterbatasan tersebut maka dipilih cara komputasi untuk menyelesaikannya dan dalam hal ini dipilih Matlab untuk menyelesaikannya.
Menggunakan Matlab untuk menyelesaikan berarti harus memandang setiap citra selain sebagai kumpulan pixel juga citra dipandang sebagai matriks. Matlab bisa mengidentifikasi setiap citra sebagai matriks terbatas pada ektensi tertentu yaitu setiap citra dengan ekstensi berikut.
|
Format |
Deskripsi |
Ekstensi |
|
TIFF |
Tagged Image File Format |
.tiff , .tif |
|
JPEG |
Joint Photographic Expert Group |
.jpeg , .jpg |
|
GIF |
Graphics Interchange Format |
.giv |
|
BMP |
Windows Bitmap |
.bmp |
|
PNG |
Portable Network Graphics |
.png |
|
XWD |
X Window Dump |
.xwd |
Suatu citra digital yang dinyatakan oleh Matlab mempunyai representasi matriks sebagai berikut:
/ f (1, 1) f (1, 2) ■■■ f (1 ,N) \ f (2, 1) f (2, 2) ••• f (2 ,n)
··· ··· ··· ···
f(N,1) f(N,2) ··· f(N,N)
Setiap elemen pada matriks tersebut disebut elemen citra atau pixel. Elemen f (i, j) menyatakan pewarnaan (tingkat kecerahan) pada elemen baris i kolom j. Demikian seterusnya. Pada citra skala abu-abu, besarnya elemen pada baris ke i kolom ke j tergantung dari format citra yang bersangkutan. Meskipun citra yang dinyatakan sebagai matriks posisinya koordinatnya dinyatakan oleh bilangan bulat tetapi nilai setiap koordinat tidak terbatas pada bilangan bulat tersebut. Terdapat beberapa kelas data pada Matlab yang bisa menyatakan suatu citra. Misalkan kelas uint8 dengan range [0, 255], kelas uint16 dengan range [0, 65535], kelas uint32 dengan range [0, 4294967295] dst.
-
5.1. Proses Encoding
Proses encoding dilakukan dengan cara melakukan partisi pada citra asli menjadi blok-blok berben-tuk persegi berukuran tertentu, blok-blok tersebut disebut blok range. Ada beberapa metode untuk melakukan partisi citra seperti metode fixed square dan metode quadtree. Metode quadtree bekerja dengan cara membagi suatu citra menjadi empat subcitra. Untuk subcitra yang telah memenuhi suatu tingkat kehomogenan tertentu maka subcitra tersebut tidak akan dibagi lagi. Sebaliknya jika subc-itra tidak memenuhi suatu kriteria kehomogenan tertentu maka subcitra tersebut akan dibagi lagi menjadi empat dan setiap subcitra tersebut akan diuji tingkat kehomogenannya, jika telah memenuhi kriteria maka subcitra tidak akan dibagi lagi tetapi jika subcitra tersebut belum memenuhi kriteria tertentu maka subcitra akan dibagi empat lagi dan demikian seterusnya hingga memungkinkan suatu subcitra berukuran paling kecil dan pasti memenuhi suatu kriteria kehomomogenan tertentu. Sedangkan metode fixed square diawali dengan mengambil dua sebarang citra abu-abu berukuran sama, satu sebagai citra yang akan ditemukan citra fraktalnya dan yang satu adalah citra awal. Citra awal berguna sebagai citra yang akan dikonstruksi menjadi citra fraktal yang mirip dengan sebarang citra asli. Citra asli merupakan citra yang akan ditemukan padanannya melalui proses encoding. Bagi citra awal menjadi subcitra-subcitra berukuran secara tumpang tindih (overlapping), artinya untuk setiap Di, Dj ∈ D C R2, Di ∩ Dj = , untuk i = j . Subcitra tersebut disebut dengan sel-sel domain. Selanjutnya citra asli dipartisi menjadi subcitra-subcitra yang tidak saling tumpang tindih dengan ukuran n × n pixel, artinya untuk setiap Rk, R — i ∈ R2, Rk ∩ Ri = untuk k = 1. Subcitra-subcitra tersebut selanjutnya disebut sel-sel range. Proses utama dari encoding adalah menemukan sel domain yang mirip dengan sel range untuk semua sel range pada setiap sel domain. Pencocokan sel range dengan sel domain hanya mungkin jika ukuran tiap sel range dan sel domain sama. Untuk memenuhi syarat tersebut maka ukuran sel-sel domain diperbaharui dari berukuran 2n × 2n menjadi sama dengan ukuran sel range yaitu n × n . Proses ini dilakukan dengan cara mengambil rata-rata dari setiap bagian sel domain berukuran 2 × 2 pixel diartikan sebagai 1 pixel.
Untuk setiap sel range akan dicari sel domain yang paling mirip. Proses pencarian sel domain tersebut menggunakan transformasi affine. Diambil sebarang sel range Rk,l yaitu sel range yang terletak pada baris ke k dan kolom ke j . Pencarian sel domain bisa dilakukan dengan aturan tertentu atau bisa dilakukan urut berdasarkan baris dan kolom. Untuk setiap sel domain Di,j uji kemiripannya dengan Rk,l . Uji kemiripan pertama kali dilakukan secara langsung atau menggunakan transformasi identitas, selanjutnya hasil tersebut dibandingkan kemiripannya setelah Di,j dikenakan transformasi antara lain rotasi 90o, rotasi 180o, rotasi 270o , putar poros horisontal dan putar poros vertikal. Hasil setiap perbandingan dicatat dan pilih Di,j yang paling mirip Rk,l . Proses dilanjutkan untuk sel domain yang lain dan untuk sel range yang lain.
Proses pencarian dan pencocokan bagian-bagian citra dari sel range dan sel domain merupakan bagian yang sangat rumit terutama dari waktu yang dibutuhkan. Pengembangan suatu algoritma untuk proses encoding bisa dilakukan untuk meminimalkan waktu tersebut. Sifat kesebangunan diri lokal (local self-similarity) bisa digunakan untuk mengembangkan efisiensi mekanisme pencarian domain.
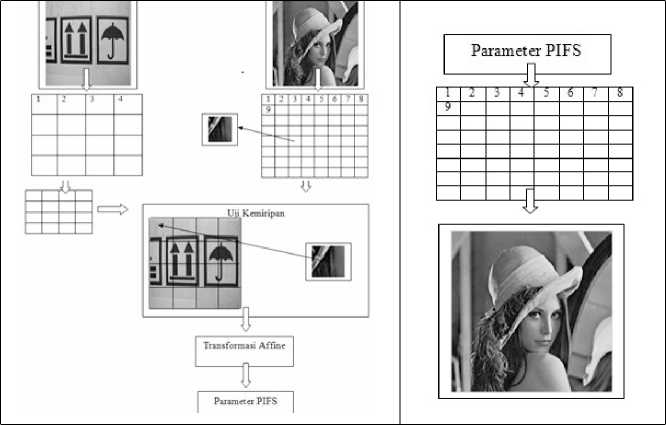
Gambar 1 Skema Encoding dan Decoding
-
5.2. Proses Decoding
PIFS yang diperoleh dari proses encoding merupakan dasar dari proses decoding. Untuk memulai proses decoding, informasi yang tersimpan dalam PIFS diambil dan selanjutnya siap untuk diit-erasikan.




Gambar 2 Citra Fraktal Lena

Citra Oldhouse

iterasi 3

iterasi 1

iterasi 5

iterasi 2

iterasi 10
Gambar 2 Citra Fraktal Lena Ukuran Blok Range 4 × 4 Pixel
Gambar 3 merupakan citra fraktal Lena dengan citra awal Oldhouse. Dari hasil tersebut terlihat bahwa untuk ukuran partisi dengan ukuran blok range semakin kecil maka hasil yang diperoleh lebih halus dan lebih mencerminkan citra aslinya. Meskipun demikian, waktu yang diperlukan untuk memperoleh citra fraktal dengan partisi pixel yang mengecil memerlukan waktu lebih lama.
Hasil dari inves fraktal pada citra tersebut merupakan IFS yang disusun dari 8 transformasi dengan menyertakan alamat pasangan blok range dengan blok domain beserta ukuran mengkerutnya. Berdasarkan proses dan hasil yang diperoleh, ada beberapa hal yang menjadi kelebihan dan permasalahan yang muncul pada saat melakukan proses iterasi untuk mendapatkan citra fraktal dari sebarang citra awal sehingga kedua citra tersebut mirip. Masalah pokok yang muncul adalah rumitnya proses encoding dengan tingkat kompleksitas komputasi yang cukup tinggi sehingga waktu yang diperlukan untuk melakukan proses encoding sangat lama, tidak sebanding dengan waktu yang diperlukan untuk proses decoding. Hal tersebut dapat dilakukan untuk penelitian lebih lanjut untuk lebih memperpendek waktu encoding misalkan dilakukan pemrograman paralel. Permasalahan yang kedua adalah citra yang digunakan masih merupakan citra dalam skala abu-abu, hal tersebut dapat diperluas untuk sebarang citra berwarna serta dari segi ukuran mungkin bisa dihilangkan syarat ukuran citra yang masih mengharuskan berbentuk persegi.
Proses pencocokan blok range dan blok domain pada bahasan diatas dikerjakan dengan bahasa Matlab. Selanjutnya bisa dikembangkan untuk menggunakan bahasa pemrograman lain seperti bahasa C, Pascal dan lainnya yang memiliki toolbox-toolbox yang berbeda sehingga bisa diharapkan memberikan hasil yang lebih baik. Pengembangan tetap bisa dilakukan pada penyelesaian masalah waktu encoding yang lebih singkat. Hal lain yang masih bisa dikerjakan adalah pembuatan blok range dan blok domain yang mungkin bisa tidak berbentuk persegi.
IFS dan Hasil Iterasinya
|
w |
a |
b |
c |
d |
e |
f |
g |
|
1 |
0,5 |
0 |
0 |
0,5 |
1 |
1 |
0,33 |
|
2 |
0,5 |
0 |
0 |
0,5 |
1 |
50 |
0,33 |
|
3 |
0,5 |
0 |
0 |
0,5 |
50 |
50 |
0,34 |
Tabel 1 IFS dari Segitiga Sierpinski
|
w |
a |
b |
c |
d |
e |
f |
g |
|
1 |
0 |
0 |
0 |
0,16 |
0 |
0 |
0,01 |
|
2 |
0,85 |
0,04 |
-0, 04 |
0,85 |
0 |
1,6 |
0,85 |
|
3 |
0,2 |
-0, 26 |
0,23 |
0,22 |
0 |
1,6 |
0,07 |
|
4 |
-0, 15 |
0,28 |
0,26 |
0,24 |
0 |
0,44 |
0,07 |
|
Tabel 2 IFS dari Pakis Barnsley | |||||||
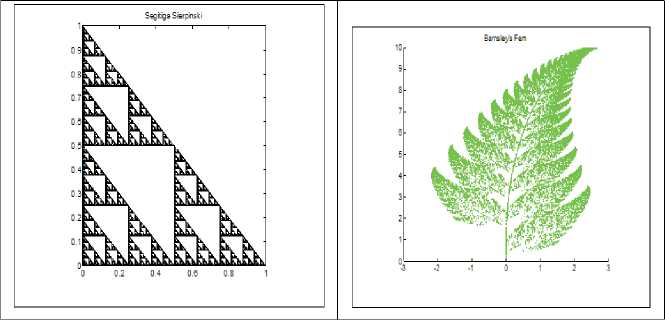
Gambar 4 Hasil Iterasi dari IFS
References
-
[1] Barnsley, M. F., 1988, Fractals Everywhere, Academic Press, Inc., London
-
[2] Becker, Karl-Heinze, 1989, Dynamical Systems and Fractals : Computer Graphics Experiment in Pascal, Cambridge University Press, Cambridge.
-
[3] Devaney, R., L., 1992, A First Course In Chaotic Dynamical Systems, Theory And Experiment, Addison Wesley Publishing Company,Inc., Boston
-
[4] Edgar, Gerald, 2007, Measure, Topology, and Fractal Geometry, Second Edition, Springer, USA
-
[5] Falconer, Kenneth, 2003, Fractal Geometri, Mathematical Foundation And Application: Second Edition, John Wiley And Sons, Ltd, England
-
[6] Falconer, Kenneth, 1997, Techniques in Fractal Geometri, John Wiley And Sons, England
-
[7] Fisher, Y, 1995, Fractal Image Compression : Theory And Appliation , Springer-Verlag New York, Inc, New York
-
[8] Gonzales R.C., 2005, Digital Image Processing Using Matlab, Prentice Hall, Upper Saddle River, New Jersey
-
[9] Helmberg, Gilbert, 2007, Getting Acquainted with Fractals, Walter de Gruyter, GmbH and Co, Berlin, Germany
-
[10] Hoggar, S.,G., 2006, Mathematics of Digital Images: Creation, Compression, Restoration, Recognition, Cambridge University Press, New York
-
[11] Liebovitch, L.,S., 1998, Fractals and Chaos : Simplified for The Life Sciences, Oxford University Press, Oxford
-
[12] Lowen, S.,G., Teich,M.,C., 2005, Fractal Base Point Processes, John Wiley and Sons, Inc, Hobogen, New Jersey
-
[13] Mandelbrot, Benoit B., 1982, The Fractal Geometry of Nature, WH Freeman and Company, New York
-
[14] Nikiel, Slawomir, 2007, Iterated Function Systems for Real-Time Image Synthesis, Springer Verlag London Limited, London
-
[15] Pietgen,H.O., 2004, Jurgens,H., and Saupe, D., Chaos and Fractals : New Frontiers of Science, Second Edition, Springer-Verlag New York, Inc., New York
-
[16] Pitas, Ioannis, 1993, Digital Image Processing Algorithms, Prentice Hall International (UK) Ltd
-
[17] Soberano, Lisa, A., 2000, The Mathematical Foundation of Image Compression, University of North Carolina at Wilmington, North Carolina
-
[18] Steven, Roger T., 1990, Advanced Fractal Programming In C, M &T Publishing, Inc., Redwood City
-
[19] Utomo,B,. 2010, Implementasi Teorema Collage pada Citra, Tesis, Jurusan Matematika, Universitas Gadjah Mada, Jogjakarta
-
[20] Widodo, 2010, Entropi Sistem Dinamika Diskrit dan Penerapannya Pada Entropi Barisan DNA, Pidato Pengukuhan Guru Besar dalam Bidang Ilmu Matematika, Fakultas MIPA, Universitas Gadjah Mada, Jogjakarta
Discussion and feedback