Estimasi Nilai AVaR Menggunakan Model GJR dan Model GARCH

Jurnal Matematika Vol. 5 No.2, Desember 2015. ISSN: 1693-1394

Estimasi Nilai AVaR Menggunakan Model GJR dan Model GARCH

Komang Dharmawan

Jurusan Matematika, Fakultas MIPA, Universitas Udayana e-mail: [email protected]

Abstrak: Dalam pemodelan harga saham, sering dihadapkan pada suatu pertanyaan, apakah model GARCH atau GJR yang lebih tepat merepresentasikan pergerakan harga saham? Secara teori, model GJR adalah perbaikan dari model GARCH, karena model GJR melibatkan parameter ketaksimetrisan. Untuk menjawab pertanyaan ini, maka dipandang perlu untuk melakukan kajian terhadap kinerja kedua model tersebut khususnya dalam mengestimasi risiko pasar. Tujuan dari makalah ini adalah mengestimasi nilai VaR dan AVaR menggunakan model model GARCH dan GJR kemudian membandingkan kinerja kedua model tersebut dalam memodelkan risiko investasi pada saham PT. Telkom. Hasil kajian menunjukan bahwa VaR dan AVaR dengan pendekatan model GJR memberikan agresifitas yang lebih tinggi jika dibandingkan dengan model GARCH.

Kata kunci: VaR, Average VaR, GARCH, GJR, Volatilitas Bersyarat.

• 1.    Pendahuluan

Pengelolaan risiko telah mengalami kemajuan yang sangat pesat pada dua dekade terakhir. Hal ini ditandai dengan munculnya suatu metode baru, yaitu metode VaR (Value at Risk) dalam pengukuran risiko pada tahun 1990an. VaR didefinisikan sebagai kerugian maksimum yang dialami oleh investor untuk suatu probabilitas tertentu yang didefinisikan sebagai tingkat kepercayaan (confidence level), selama suatu periode waktu tertentu. VaR biasanya digunakan oleh lembaga efek atau bank investasi untuk mengukur risiko pasar dari portofolio investasi. Sampai saat ini metode ini telah menjadi acuan standar dalam pengelolaan risiko pada beberapa institusi keuangan.

Meskipun demikian, VaR memiliki sejumlah kekurangan yang diakui oleh para profesional di bidang finansial. Salah satu kelemahannya adalah VaR tidak bersifat subadditif. Artinya, ketika dilakukan diversifikasi pada portofolio ada nilai VaR saham pembentuk portofolio yang nilai VaR-nya lebih besar dari nilai VaR portofolio itu sendiri. Ini berarti ada kasus dimana VaR portofolio lebih kecil dari salah satu VaR dari saham-saham yang membentuk portofolio. Sifat ini menunjukkan bahwa VaR yang tidak dapat digunakan sebagai alat ukur risiko yang akurat. Sebagai alternatif, Average Value at Risk (AVaR) dapat dipilih sebagai alat ukur risiko yang lebih handal.

Keunggulan yang dimiliki AVaR adalah AVaR memiliki interpretasi intuitif, yaitu dalam hal komputasi dan portofolio optimal, suatu hal yang sangat disukai oleh praktisi keuangan yang memiliki latar belakang matematika yang kuat. Selain itu, AVaR memenuhi semua aksioma mengenai sifat risiko yang koheren dan konsisten dalam kaitannya dengan investor yang bersifat risk-varse.

AVaR adalah salah satu produk yang dihasilkan dari kemajuan dalam bidang pengelolaan risiko. Hal ini tidak terlepas dari penemuan baru dalam bidang peramalan atau estimasi nilai volatilitas. Sifat heteroskedastik yang ditunjukkan oleh adanya ketakstasioneran dalam volatilitas, telah menyebabkan adanya volatility clustering, yaitu suatu fenomena dimana volatilitas akan tetap pada gerakan level tinggi untuk beberapa periode ketika volatilitas mengalami tren naik, atau sebaliknya akan tetap rendah untuk beberapa periode ketika volatilitas mengalami tren turun (Engle [4]). Ketika sifat ini diabaikan, tidak dilibatkan dalam model, maka kemungkinan terjadinya hasil peramalan yang menyimpang jauh dari hasil sesungguhnya sangat besar.

Penerapan model varians bersyarat atau GARCH berserta seluruh keluarga GARCH, diharapkan akan mampu mananggulangi masalah heteroskedastik. Engle [3] mengusulkan model ARCH, Autoregressive Conditional Heteroskedasticity, untuk memecahkan permasalahan ini, namun 4 tahun kemudian muncul metode yang sifatnya lebih umum, yaitu model GARCH yang diusulkan oleh Bollerslev [2]. Untuk beberapa kasus, model ARCH tampil identik dengan model GARCH, seperti seperti model GARCH(1,1) ekivalen dengan model ARCH dengan 2 lag (Bauwens, et al. [1]). Model GARCH merupakan bentuk yang lebih umum dari model ARCH, sehingga pengembangan model GARCH lebih mudah dilakukan. Beberapa model lain, seperti GJR yang mengambil nama dari pengebangnya yaitu Glosten, Jagannathan and Runkle [5]. Model lain seperti T-GARCH yang dikembangkan oleh Zakoïan pada tahun 1994 atau EGARCH oleh Nelson pada tahun 1991 merupakan model GARCH dengan respon yang tak simetris (Bauwens, et al. [1]). Pertanyaan yang sering muncul adalah keluarga GARCH yang mana yang mesti dipakai untuk memodelkan varians bersyarat? Dalam makalah ini akan dibahas model GARCH dan salah satu keluaganya, yaitu model GJR serta kinerjanya dalam menaksir VaR dan AVaR.

• 2.    Model GJR

Sebelum membahas model GJR ada baiknya melihat kembali model GARCH yang banyak dibahas pada berbagai literatur seperti pada Bollerslev [2], atau Bauwens, et al. [1]. Misalkan {r_t, t = 1, — ,T} adalah tingkat pengembalian (return) suatu aset yang mengikuti model AR(1) dan model GARCH(1,1) dengan standard innovation yang masing-masing mengikut distribusi normal standar N (0,1) atau distribusi t, yaitu

r_t =   + Cιr_t-ι + c_t dengan C_t =                      (1)

^σ_t =   + UlC_t-₁ + β°t-l, dan                      (2)

^zt ^~N(0,1) atau ^zt ~ id .

Dalam hal ini, E L adalah residual dari model, μ_t =( ^rt)=E(E( ^rt |Ωt-ι)) adalah rataan bersyarat dari return, dan ^σt = Var(^rt |Ωt-ι) =Var(Z^ |Ωt-1) adalah varian bersayat, dengan ^aO >0, a₁≥0,β≥0, dan a₁ +β<0, dimana Ωt-ι adalah himpunan semua informasi masa lalu sampai pada t-1. Dalam kasus normal nilai a₁ +β<1. Dengan kondisi ini sudah cukup untuk mendapatkan matriks kovarian yang setasioner. Dengan demikian, keadaan ini akan menyebabkan nilai dari varian tak bersyarat akan berhingga, sedangkan nilai varian bersyarat σ_t merupakan fungsi dari waktu t (Bauwens, et al. [1]). Dalam kasus distribusi tak normal, syarat a₁Var(^rt)+ β<1, Huang et al [6].

σ² = Var(r_t)=                                   (3)

1-α₁ ^- - ^-β

angka pada persamaan (3) datang dari asumsi normal pada ^zt , secara intuitif datang dari asumsi bahwa disrubusi bersyarat dari return adalah simetri disekitar E- .

Misalkan diberikan suatu model GJR dengan rataan menghikuti inovasi berdistribusi normal atau berdistribusi t, maka model GJR(1,1) secara matematis diberikan oleh

r_t =   + ClT_t-ι + c_t dengan c_t =

(4)

σ_t =   + UlC_t-₁ + β CYt-I + Yβ-ιC_t-ι, dan

^zt ^~N(0,1) atau ^zt ~ id

dimana 1^ — 1

={ .

1₀,_,

C_t-I <0

C_t-I ≥0

distribusi marjinal bersyarat dari ^^t+l untuk model GJR hampir sama dengan model GARCH, yang didefinikan sebagai berikut

p(^rt+ι ≤ ̅|Ωt)

( ̅-μ)

|Ω ■⁾

=(^zt+ι ≤

√ «o + «i^t-i + β⅛-ι + Yk-i^t-i

N

id

(√

(√

( ̅~μ)

a_o+a₁ε^₁+βσ^₁+γl_t-₁ε^₁

( ̅ ~μ)

a_o+a₁ε^₁+βσ^₁+γl_t-₁ε^₁

|Ω ^!)

|Ω '⁾

jika Z_t ~N(0,1)

jika ^zt ^~ td

(5)

• 3.    Average Value at Risk (AVaR)

Apakah akan menggukan VaR atau AVaR dalam pengelolaan risiko? Secara teori, kedua pengukuran risiko ini memiliki perbedaan yang sangat fundamental, yaitu VaR adalah suatu kuantil sedangkan AVaR adalah ekspektasi berysarat dari ekor distribusi. Kedua alat ukur risiko tersebut akan identik apabila ekor distribusi dari peubah acaknya dihilangkan/dipotong. Untuk lebih memahami, perhatikan ilustrasi yang disajikan pada Gambar 1.

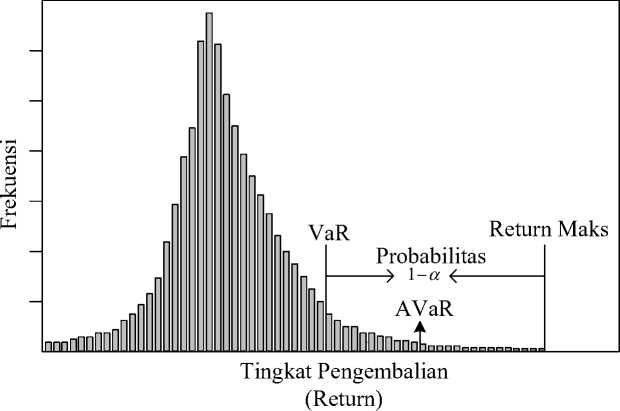
Gambar 1. Hubungan antara VaR, AVaR, dan nilai return maksimum

Jadi nilai AVaR berada antara nilai VaR dan return maksimum. Tampak dari ilustrasi pada Gambar 1, VaR dan AVaR adalah dua alat ukur yang berkaitan dan AVaR fungsi kontinu dari return dan bersifat cembung (convex). Atas dasar kedua sifat ini, maka AVaR dikatakan memiliki sifat ‘coherent’ sehingga lebih menarik untuk ditelaah dari sudut pandang

matematika. Karena sifat ini juga, fungsi AVaR dapat lebih mudah dioptimalkan dengan metode pemrograman linier jika dibandingkan dengan VaR. Pembaca yang tertarik dengan sifat AVaR dan keunggulannya dibanding VaR dapat mengacu ke Rachev et al. [10], Pflug [9], atau Sarykalin et al. [11].

Sebelum membahas VaR lebih jauh, ada baik mengenal apa itu risiko terlebih dahulu. Risiko dapat didefinisikan sebagai volatilitas dari kejadian yang tidak diharapkan Jika risiko dikaitkan dengan alat ukurnya, maka VaR adalah alat ukur risiko (Jorion [7]). Jika diberikan suatu aset, maka VaR dari aset tersebut pada saat t dengan tingkat kepercayaan (1-a), dimana a ∈ (0,1), adalah

VaRt(a) = inf{ ^rt ∶   ( ^rt)≥a}

(6)

dimana F_t fungsi distribusi dari tingkat pengembalian aset (return) ^rt pada saat t atau P(^rt ≤VaR L (a)|Ωt-ι)=a . Ini berarti bahwa dengan tingkat kepercayaan 100(1 -a)% bahwa kerugian yang pada selang waktu Δt tidak akan melebihi VaR, dimana Ωt-ι adalah himpunan semua infomasi mengenai saham tersebut sampai pada t-1, atau

VaR

P(^rt ≤VaRt

(a)|Ωt-ι)=∫

— ∞

f( ^rt|Ωt-l) dr

(7)

dimana f(⋅) adalah fungsi densitas dari ^rt . Misalkan Ft =( ^rt ) dan σ_t = Var(^rt), dan misalkan VaRf menyatakan a100% VaR untuk satu hari ke depan, maka

(^rt -F   VaR_t-FI ∖

^p(-  _≤ VaR - _{|Ω t}-l)=^a

VaR _t -FI ∖ ^p( Zt ^≤ VaR - _|Ω t-l)=a

VaR_t= + ^σt Φ-¹ (a ₎                          (8)

dengan Φ ¹ (⋅) adalah fungsi invers dari fungsi distribusi kumulatif normal standar. Karena fungsi distribusi normal standar adalah simetri, maka untuk mendapatkan nilai VaR yang positif, persamaan (8) dapat dikalikan dengan (-). Dengan demikian, maka menggunakan definisi dari AVaR seperti dibahas dalam Rachev et al. [10] atau Sarykalin et al [11], maka AVaR dari ^rt dengan tingkat kepercayaan a ∈ [0,1] adalah rataan dari distribusi generalized a-tail, yaitu

AVaRa(r)

=-¹∫ Pr (_s) ds

a

(9)

Persamaan (9) dapat dibaca sebagai rata-rata dari semua peritiwa yang lebih besar dari VaRα( ^rt) atau rata dari semua peristiwa yang lebih kecil dari -VaRa( ^rt ) . Dalam makalah ini nilai AVaR a( ^rt ) akan dihitung dari nilai rata-rata dari semua peristiwa yang lebih kecil dari -VaR a( r_t).

• 4.    Studi Empiris

Tujuan dari penelitian ini adalah menguji kinerja dari model AR(1)-GJR(1,1) dalam mengesitmasi nilai VaR dan CVaR dengan membandingkannya dengan AR(1)-GARCH(1,1). Data yang dipakai dalam analisis adalah data harga penjualan harian saham Telkom yang dicatat pada 14 April 2013 -12 April 2016 terdapat 778 observasi. Data tingkat pengembalian (return) disajikan pada Gambar 2b, dihitung menggunakan rumus r_t =ln( ⅜+ι/ )

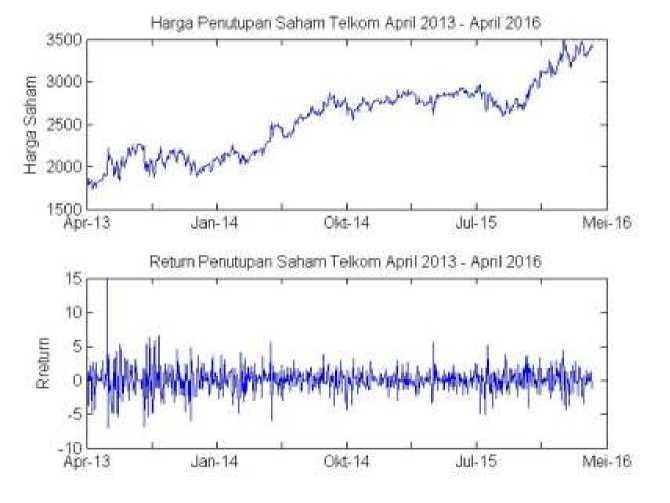
Gambar 2. (a) Pergerakan harga saham harian Telkom pada periode April 2013-April 2016. (b) Return harga saham harian pada periode April 2013-April 2016

• 4.1    Statistik Deskriftif Data

Tabel 1 berikut ini menyajikan empat momen pertama, yaitu rataan, deviasi standar, skewness, dan, kurtosis dan uji Jarque-Bera dari data return. Dari momen ketiga data terlihat bahwa return PT Telkom menunjukkan adanya skewness sebesar 0.4011, artinya data tidak simetris. Kemudian dari momen keempat data (kurtosis) terlihat bahwa data memiliki ekor gemuk (9.2420), untuk distribusi normal, kurtosis memiliki nilai 3. Jadi serara keseluruhan data return PT Telkom pada periode tersebut tidak normal. Hal ini juga didukung oleh hasil uji Jarque-Bera (JB Test).

Tabel 1. Statistik Deskriptif Saham Telkom Periode 16 April 2013-17 April 2016

Statistik	Nilai
Rataan	0.0804
Deviasi Standar	1.8523
Skewness	0.4011
Kurtosis	9.2420
JB Test	H=1 p=0.0001

• 4.2    Uji autokorelasi

Dalam uji autokorealsi digunakan uji Ljung-Box. Tujuan dari uji ini adalah untuk melihat apakah return atau tingkat pengembalian dari PT Terkom berotokorelasi atau tidak. Hasil uji ini menunjukan penerimaan hipotesis alternatifH₁ dengan p = [0.0000 0.0003 0.0013] untuk taraf signifikan a = [5% 10% 15%]. Dari hasil uji ini tingkat pengembalian (return) data saham PT. Telkom menunjukkan adanya sifat autokorelasi cukup signifikan, jadi pemodelan return dengan AR(1) adalah valid. Selain dengan uji Ljung-Box, secara virtual juga terlihat pada Gambar 2, bahwa adanya sifat autokorelasi cukup jelas. Perhatikan bahwa adanya titik-titik yang melewati dua garis horizontal yang sejajar pada lag-lag tertentu. Dengan demikian, pemilihan model ^rt = ^co + ^c₁ ^rt - ₁ + ^£ t cukup representatif untuk menyajikan data return.

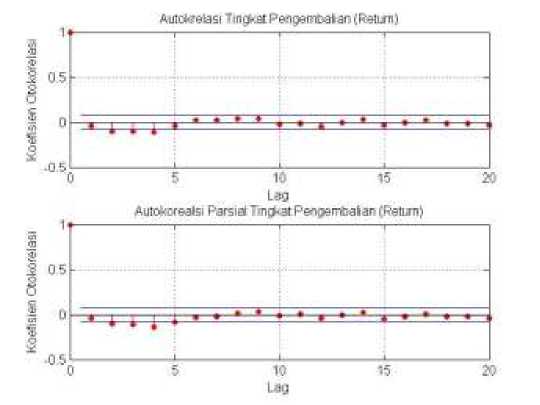
Gambar 2. (a) Autokorealsi retun PT Telkom, (b) Autokorelasi parsial retun PT Telkom

• 4.3    Uji Heteroskedastik

Untuk mangetahui ada tidaknya sifat heteroskedatik, yaitu sifat ketakstasioner data dalam varians maka dilakukan uji Engle's ARCH untuk 2 lag. Hasil uji ini menunjukkan penerimaan hipotesis alternatif H-^ dengan P =0 . Dengan ditolaknya hopotesis nol, maka hasil ini menyarankan model GARCH atau GJR cukup sesuai untuk memodelkan varians data return PT. Telkom. Pertanyaannya sekarang kenapa GARCH(1,1) atau GJR(1,1)? Pada dasarnya ketika melakukan uji dengan Engle's ARCH untuk 2 lag, pada saat yang sama kita menguji kelayakan model GARCH(1,1) karena model ARCH dengan inovasi 2 lag adalah ekivalen dengan model GARCH(1,1) (Huang, et al., 2010). Selain uji Engle's ARCH untuk 2 lag, secara virtual juga terlihat dari Gambar 3, bahwa varians memang memiliki sifat heteroskedastik, jadi penerapan GARCH maupun GJR bersyarat menjadi cukup valid dalam memodelkan data PT. Telkom.

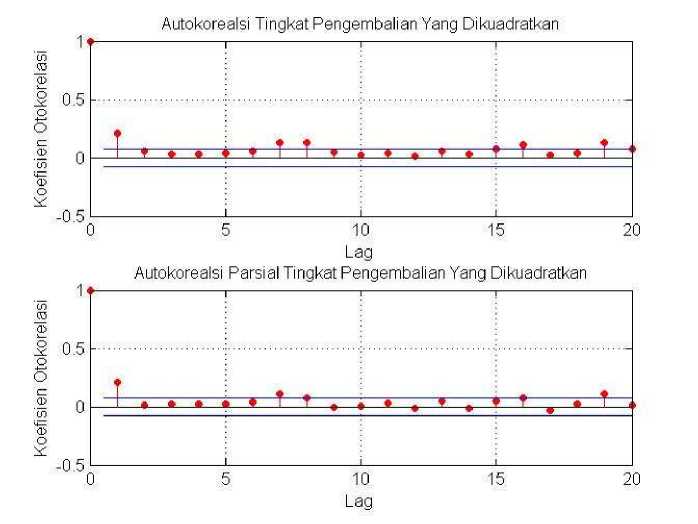
Gambar 3. (a) Autokorealsi Parsial kom, (b) Autokorelasi parsial retun PT Telkom

Tabel 2. Hasil estimasi parameter GARCH dan GJR, angka dalam kurung adalah eror standar dari masing maing parameter. Mengacu ke nilai AIC, BIC, dan Loglikehood pada Tabel 2 terlihat bahwa model GJR(1,1) lebih sesuai dengan data Telkom dibandingkan dengan GARCH(1,1), yaitu nilai AIC, BIC, dan Loglikehood dari GJR lebih kecil dibandingkan dengan nilai tersebut dari GARCH, namum perbedaan itu tidak begitu signifikan.

Tabel 2. Estimasi parameter dan eror standar untuk data Telkom periode 16 April 2013-17 April 2016

Parameter	Model AR(1)-GARCH(1,1)		Model AR(1)-GJR(1,1)
	Dist. N(0,1)	Dist. t	Dist. Normal	Dist. t
Co	0.0773 (0.057)	0.1208 (0.048)	0.0635 (0.055)	0.1208 (0.051)
Cl	-0.0312 (0.044)	-0.0760 (0.038)	-0.0330 (0.048)	-0.0760 (0.039)
«0	0.0190 (0.015)	0.0160 (0.031)	0.0183 (0.017)	0.0160 (0.032)
a1	0.0189 (0.008)	0.0360 (0.025)	0.0141 (0.011)	0.0359 (0.020)
β	0.9737 (0.012)	0.9620 (0.031)	0.9721 (0.014)	0.9621 (0.033)
Y	-	-	0.0129 (0.021)	0.0000 (0.023)
AIC	-3076.4253	-2969.8803	-3076.4971	-2969.1697
BIC	-3099.7025	-2993.1575	-3105.4298	-3001.7578
Log Likelihood	1533.213	1479.940	1532.749	1477.585
D.K.		4.000 (0.603)		4.000 (0.606)

Dari data yang tersaji pada Table 2, dapat ditulis model yang lebih spesifik yaitu

• (a)    Model AR(1)-GARCH(1,1) dengan inovasi Z_t =   ~N(0,1)

r_t = 0.0773 - 0.0312 ^rt-ι + ε_t

σ_t = 0.0190 + 0.0189 ^εt-l + 0.9737^σt-ι,

• (b)    Model AR(1)-GARCH(1,1) dengan inovasi ^zt ₌   ~t

^rt = 0.1208 - 0.0760^rt-l + ^εt

^σL = 0.0160 + 0.0360^εt-l + 0.9620^σt-ι,

• (c)    Model AR(1)-GJR(1,1) dengan inovasi ^zt ₌   ~N(0,1)

^rt = 0.0635-0.0330^rt-ι + ^εt

Ot = 0.0183 + 0.0141ε_t.₁ + 0.9721^σt-ι + 0.0129 h-ι^εt-ι

(d) Model AR(1)-GJR(1,1) dengan inovasi ^zt ₌   ~ t_d dimana     ={

1₀,_,

^εt-l <0

^εt-l ≥0

^rt = 0.1208 -0.0760^rt-l + ^εt

Ot = 0.0160 + 0.0359^εt-l + 0.9621^σt-ι + 0.0000 h-ι^εt-ι

Untuk model (d) terlihat bahwa Y=0 , artinya model (d) pada dasarnya adalah model GARCH, jadi ketika Y=0 model GJR adalah model GARCH.

Berikut ini adalah langkah-langkah dalam menghitung VaR dan AVaR. Misalkan ^rt-ι dan ^σt-ι adalah return dan volatilitas observasi terakhir dari sampel data, maka menggunakan model (a)-(d) di atas dapat diestimasi nilai-nilai VaR dan AVaR sebagai berikut

VaR_t=   + ^σt Φ (0.05) = -(-1.3353 + 1.5614 × -1.6449)

= 3.9036

Sedangkan AVaR dihitung menggunakan

AVaR = -Е(r_t |^rt-l < -3.9036)) = 5.1560

Hasil 5.1560 adalah rata-rata dari semua nilai ^rt yang lebih kecil dari VaR L . Dengan cara yang sama hasil keseluruhan perhitungan dapat dilihat pada Tabel 3.

Tabel 3. Estimasi VaR dan AVaR untuk pada a = 0.05

Pengukuran Risiko	GARCH		GJR
	Normal	t	Normal	t
VaR	3.8920	4.6640	3.8862	4.6758
AVaR	5.0253	5.4101	5.0253	5.5117

Dari hasil esitmasi seperti pada Tabel 3 terlihat bahwa VaR yang diestimasi menggunakan model GARCH(1,1) dan GJR(1,1) tidak menunjukkan adanya perbedaan yang berarti. Hasil ini memang sesuai dengan nilai AIC, BIC, dan Loglikehood dari dari kedua model. Hal ini mengindikasikan bahwa efek dari Y seperti terlihat pada persamaan (4) tidak begitu berpengaruh untuk kasus data Telkom, karena memang nilai kemencengannya (skewnes) sangat kecil yaitu 0.4011 (Tabel 1). Hasil ini tidak jauh berbeda dengan penelitian yang dilakukan oleh Su et al [12]. Dalam penelitiannya Su et al [12] menaksir return data holdings dari FuBon and Cathay financial menggunakan ARMA(1,1) sedangkan dalam penelitian ini digunakan AR(1). Namun hasil yang berbeda didapatkan oleh Lee and Liu [8]. Hasil simulasi yang dilakukan oleh Lee and Liu [8] untuk data Indeks NasDaq-500 dan 10-year Trasury menunjukkan bahwa GARCH(1,1) lebih cocok dibandingkan dengan GJR(1,1) dalam memodelkan data tersebut.

• 5.    Kesimpulan

Dalam makalah ini, telah dibahas dua model time series, yaitu model GARCH dan model GJR yang dipakai untuk mengestimasi return dan volatilitas bersyarat dari harga saham PT. Telkom. Kedua model menunjukkan kinerja yang tidak jauh berbeda ketika dipakai untuk mengestimasi VaR atau AVaR. Dari momen ke tiga dan momen keempat data (kurtosis) terlihat bahwa data memiliki ekor gemuk (9.2420), untuk distribusi normal, kurtosis memiliki nilai 3. Jadi serara keseluruhan data return PT. Telkom pada periode tersebut tidak normal. Hal ini juga didukung oleh hasil uji Jarque-Bera (JB Test). Uji autokorelasi menunjukkan bahwa ini tingkat pengembalian (return) data saham PT. Telkom menunjukkan adanya sifat autokorelasi cukup signifikan, jadi pemodelan return dengan AR(1) adalah valid. Hasil uji

heteroskedastisitas menunjukkan adanya varians yang tidak konstan, sehingga model GARCH atau GJR adalah pilihan yang sesuai untuk memodelkan varians data return PT. Telkom. Secara keseluruhan dapat disimpulkan bahwa untuk kasus data dengan efek ketaksimetrisan yang kecil model penggunaan GARCH atau GJR tidak akan memberikan pengaruh terhadap hasil estimasi data time series, khususnya data yang memiliki sifat autokorelasi atau heteroskedastik yang signifikan

Daftar Pustaka

• [1]    Bauwens, et al. 2012. Handbook of Volatility Models and Their Applications. First Eds, John Wiley and Sons, Inc.

• [2]    Bollerslev, T. 1986. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics. Vol. 31, 1986, pp. 307327.

• [3]    Engle, R. F. 1986. Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica. Vol. 50, pp. 9871007

• [4]    Engle, R. F. 2001. GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics. Journal of Economic Perspectives 15:4

• [5]    Glosten, L. R., R. Jagannathan, and D. E. Runkle. 1993. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance. Vol. 48, No. 5, 1993, pp.1779-1801.

• [6]   Huang, J., et al. 2010. Estimating value at risk of portfolio by conditional copula-GARCH

method. Insurance: Mathematics and Economics

• [7]    Jorion P. 2002. Value at Risk: The New Benchmark for Managing Financial Risk. 2^nd edition. McGraw-Hill

• [8]    Lee, D and D. Liu. 2014. Monte-Carlo Simulations of GARCH, GJR-GARCH and constant volatility on NASDAQ-500 and the 10 year treasury. Duke University Technical Report April, 21, 2014.

• [9]    Pflug G. C. 2000. Some Remarks on the Val-ue-At-Risk and the Conditional Value-At-Risk In: S. Uryasev, Ed., Probabilistic Constrained Optimization: Methodology and Applications, Kluwer Academic Publishers, Dordrecht.

• [10]    Rachev, S. T. et al. 2007. Advanced Stochastic Models, Risk Assessment, and Portfolio Optimization : The Ideal Risk, Uncertainty, and Performance Measures. John Wiley.

• [11]    Sarykalin et al. 2008. Value-at-Risk vs. Conditional Value-at-Risk in Risk Management and Optimization. Tutorial in Operation Research. INFORMS:   doi

10.1287/educ.1080.0052

• [12]    Su, Y. C., H. C. Huang, dan Y. J. Jin. 2011. GJR-GARCH model in value-at-risk of financial holdings. Applied Financial Economics,  21:24,  1819-1829, DOI:

10.1080/09603107.2011.595677

127