Model Matematika (Nonlinier) Populasi Anjing Rabies dengan Vaksinasi
on
Jurnal Matematika Vol. 5 No.1, Juni 2015. ISSN: 1693-1394
Model Matematika (Nonlinier) Populasi Anjing Rabies dengan Vaksinasi
Ahmad Fitri
Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: farrel_ahmed@yahoo.com
Tjokorda Bagus Oka
Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: tjokordabagusoka@gmail.com
I Nyoman Widana
Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: nwidana@yahoo.com
Abstract: Rabies is a fatal infectious virus that can attack all mammals especially dogs. Infection happens when there is interaction between healthy dogs and rabies-infected dogs. In Bali, rabies was first found in late 2008. One of the solutions done by government to the problem is by giving vaccine to healtly dogs, so that they are not easily infected by the virus. Thus, a mathematical model is needed to analyze the development of dogs population in Bali. By using analysis of fixed point and stability on the model, the population of rabies-infected dog was affected by not only the percentage of vaccination but also the number of healthy dogs birth. Lastly, a numeric simulation by using Taylor’s series1st order was conducted to illustrate and to strengthen the result of the analysis.
Keyword: Rabies, Vaccination, Nonlinear Systems of Differential Equations
Rabies di Indonesia sudah lama ditemukan dan hampir seluruh daerah tertular virus ini (Rumlawang & Nanlohy [12]). Kasus rabies di Bali pertama kali muncul pada akhir tahun 2008 (Putra [11]). Mengingat bahwa Bali sebagai tujuan wisata nasional dan internasional. Dengan demikian jika hal tersebut dibiarkan, maka dapat berdampak buruk terhadap jumlah wisatawan yang akan mengunjungi pulau Bali (Besung, et. al [2]).
Virus rabies disebabkan oleh virus yang dikelompokkan dalam keluarga Rhabdoviridae kemudian menyerang sistem syaraf pusat sehingga berakibat fatal (Wang & Lou [14]).Virus ini bersifat menular dan dapat menyerang ke semua spesies mamalia. Kelompok mamalia yang rentan terinfeksi dan menjadi sumber virus ini
adalah anjing (Nugroho & Rahayujati [9]). Mengingat bahwa banyak masyarakat Bali yang memelihara anjing, maka akan berdampak tinggi terhadap penularan rabies. Selain itu juga banyak anjing liar yang rentan terkena virus ini.
Berbagai macam cara telah dilakukan pemerintah untuk menanggulangi masalah tersebut. Salah satunya memberikan vaksin terhadap anjing liar maupun anjing rumahan yang statusnya masih belum terinfeksi rabies (Putra [11]). Pemberian vaksin pada anjing dapat mengurangi laju penularan rabies. Akan tetapi sampai kapan hal tersebut harus dilakukan dan berapa banyak anjing yang harus diberi vaksin. Selain itu juga bagaimana mengetahui keefektifan dari pelaksanaan program tersebut sehingga populasi anjing rabies di Bali dapat dipunahkan. Oleh karena itu, diperlukan suatu penelitian untuk menganalisis seberapa besar capaian program vaksinasi sehingga dapat mengetahui perkembangan populasi anjing rabies di Bali. Untuk itu diperlukan suatu model matematika agar dapat diketahui keefektifan dari progam vaksinasi tersebut.
Berdasarkan kenyataan di atas maka penulis tertarik untuk menganalisa bentuk model matematika dalam hal pemberian vaksin pada anjing di Bali. Rabies sendiri sudah banyak diteliti. Antara lain oleh Wang & Lou [14] yang membahas model dinamik tentang rabies antara anjing dan manusia. Artikel tersebut juga menganalisis model kontrol dengan vaksinasi, pemisahan anjing sehat dengan anjing rabies dan menggabungkan keduanya. Hasil yang didapatkan adalah dengan vaksinasi lebih baik daripada yang lainnya. Pada artikel Rumlawang & Nanlohy [12] membahas tentang analisis kestabilan model penyebaran rabies. Model tersebut menggunakan model SIR dan hanya digunakan dua variabel yaitu Susceptible(S) dan Infective(I). Hasil analisis yaitu pada saat endemi populasi (I) meningkat dan setelah endemi populasi (S) akan meningkat. Pada penelitian Fitri, et. al. [7] yang membahas model matematika (linier) populasi anjing rabies dengan vaksinasi, model tersebut menggunakan sistem persamaan diferensial linier. Hasil yang didapatkan jumlah populasi anjing rabies tidak akan meningkat jika laju kelahiran dari populasi anjing sehat dibatasi. Pada penelitian ini, model yang digunakan yaitu model pada Wang & Lou [14] tetapi hanya membahas tentang populasi anjing. Model tersebut hampir sama dengan model pada tulisan Fitri, et. al. [7] akan tetapi memperhatikan faktor interaksi antara anjing sehat dengan anjing yang terinfeksi rabies dan disebut sistem persamaan diferensial nonlinier.
Pengertian dari persamaan diferensial biasa (PDB) yaitu suatu persamaan yang melibatkan turunan pertama atau lebih dari suatu fungsi yang telah ditentukan. Misalkan y = f(x) diturunkan terhadap peubah %. Persamaan tersebut dapat juga melibatkan y
sendiri atau fungsi dari % (Burghes & Borrie [4]). Persamaan diferensial memiliki solusi apabila memenuhi kondisi Lipschitz.
Definisi 1
Diberikan fungsi f(t, x) dengan domain D dalam interval ( t, x) , terdapat konstanta k >0 sehingga jika {( t, X1 ), ( t, X2)} ∈ D, maka ∣f( t, X1 ) — f (t, X2)| ≤ k∖x1 -X2I ,
funsi f memenuhi kondisi Lipschitz untuk setiap nilai xdalam D, dan k disebut konstanta Lipschitz untuk f (Cronin [5]).
Persamaan diferensial biasa nonlinier memiliki bentuk umum
d2y_f( dy j m
dx2 f Y’dx’x)
Fungsi f adalah fungsi nonlinier yang memuat variable y ,dy /dx dan x (Burghes & Borrie [4]).
Sistem persamaan diferensial adalah suatu sistem yang memuat n buah persamaan diferensial dan buah fungsi yang nilainya tidak diketahui. Fungsi tersebut jika sama dengan nol maka sistem dapat dikatakan sebagai sistem persamaan diferensial homogen. Begitu juga sebaliknya, dapat dikatakan sebagai sistem persamaan diferensial nonhomogen.
Sistem persamaan diferensial nonlinier dapat dinyatakan dalam bentuk sebagai berikut
dy1
-
= f (yι,y2 ,-,yn)
dy2
-
= f (y 1,y2 ,-,yn) dt
(2)
dyn
-
= f (y 1 ,y 2 ,-,yn)
dengan kondisi awal yi(t)) = σi, i = 1,2, ...,n atau ditulis dalam bentuk pesamaan dibawah ini
dy
-
^ = f( t)
dt
f adalah fungsi nonlinier dan kontinu (Rumlawang & Nanlohy [12]).
Nilai atau titik kesetimbangan dari suatu persamaan diferensial yaitu tidak berubah.
Definisi 2 Titik Kesetimbangan
Nilai atau titik kesetimbangan adalah solusi dari persamaan y' = g(x,y') ≡ 0 atau y = f(x) ≡ c, untuk nilai sembarang x (Lucas [8]).
Definisi 3 Titik Kesetimbangan
-
1. Titik kesetimbangan X∗ dikatakan stabil jika untuk setiap bilangan ε>0 terdapat bilangan δ>0 sedemikian hingga |%θ -X∗|<δ berlaku | X(t)-X∗|<ε untuk setiap t>0 (Edwards & Penny [6]).
-
2. Titik kesetimbangan x∗ dikatakan stabil asimtotik jika x∗ stabil dan terdapat bilangan δ>0 sedemikian hingga |%θ -X∗|<δ berlaku lim L →∞ X(t)=X∗ untuk setiap t→∞ (Edwards &Penny [6]).
Pelinieran dilakukan untuk menentukan perilaku solusi pada persekitaran titik kesetimbangan sistem (2).
Definisi 4
Sistem =(f( ̅))X disebut linearisasi sistem (2) di ̅ (Rumlawang & Nanlohy [12]).
Pelinieran terhadap sistem dapat dilakukan melalui ekspansi Taylor di sekitar titik tetap X∗ diperoleh matriks Jacobian untuk sistem (2) sebagai berikut:
(3)
|
d∆l | |
|
⎢⎡ dx |
dy ⎥⎤ |
|
⎢⎢ dJl |
dh ⎥⎥ |
|
⎣ |
⎦ |
Perilaku dinamik untuk sistem dapat diidentifikasi secara lengkap oleh nilai eigen dari matriks J pada persamaan (3), yaitu:
| λl -J|=0
∂f1 ∂f1
-
(4)
dx dy
dJl
dx dy
(Rumlawang & Nanlohy [12])
Jika A adalah sebuah matrik n×n, maka sebuah vektor taknol x pada Rn disebut vektor eigen (eigenvector) dari A jika Ax adalah sebuah kelipatan skalar dari x, yaitu:
Ax = (5)
untuk skalar sembarang λ, skalar λ disebut nilai eigen (eigenvalue) dari A , dan x dissebut sebagai vektor eigen dari A yang terkait dengan λ (Anton & Rorres [1]).
Seperti yang dituliskan dalam buku (Edwards & Penny [6]) jika diberikan sistem persaman diferensial linier
dx , dy ,
= F(x,y) , = G(x,y) (6)
at at
Jika titik (x*,y*) adalah titik kesetimbangan dari sistem persamaan diferensial (6) maka jenis kestabilan berdasarkan kajian terhadap nilai eigen λ 1 dan λ2 adalah sebagai berikut:
-
a. Jika λ2 < λ1 < 0 berupa bilangan real berbeda maka (x,y) menuju titik kesetimbangan (x*,y*) untuk t → ∞ dengan demikian titik kesetimbangan (x*,y*) disebut simpul stabil asimtotik begitu juga sebalikanya λ2 > λ1 > 0 disebut simpul tidak stabil.
-
b. Jika kedua nilai eigennya berlainan tanda dalam artian nilai eigen yang satu positif dan yang lainnya negatif (λ2 < 0 < λ1) maka titik kesetimbangan (x*, y*) disebut titik sadel dan tidak stabil.
-
c. Jika λ < 0 berupa bilangan real sama maka (x,y) menuju titik kesetimbangan (x*,y*) untuk t → ∞ dengan demikian titik kesetimbangan (x*,y*) disebut node stabil asimtotik begitu juga sebalikanya > 0 disebut node tidak stabil.
-
d. Jika berupa bilangan kompleks konjugat λ1 = p + qi dan λ2 = p — qi denganp < 0 maka (x, y) menuju titik kesetimbangan (x*, y*) untuk t → ∞ dengan demikian titik kesetimbangan (x*,y*) disebut fokus stabil asimtotik begitu juga sebalikanya jika
-
> 0 disebut fokus tidak stabil.
-
e. Jika berupa bilangan kompleks murni λ1 = qi dan λ2 = — qi dengan q ≠ 0maka (x,y) berupa elips untuk t → ∞ dengan demikian titik kesetimbangan (x*,y*) disebut center stabil tetapi tidak stabil asimtotik.
Jenis kestabilan berdasarkan bidang fase dapat dilihat pada Gambar 1 berikut:
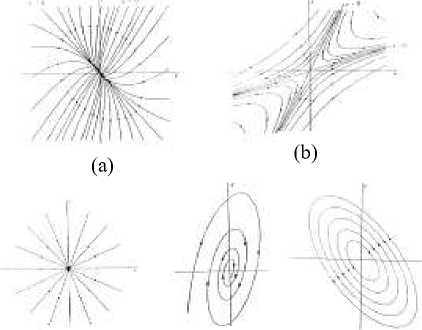
(c) (d) (e)
Gambar 1.Jenis Kestabilan dalam Bidang Fase (Edwards & Penny [6]).
Data yang digunakan adalah data sekunder tentang populasi anjing rabies di Bali dari bulan November 2011 hingga bulan November 2014 yang diperoleh dari Dinas Peternakan dan Kesehatan Hewan Provinsi Bali.
Model matematika yang dirancang merupakan sistem persamaan diferensial nonlinier orde satu nonhomogen dengan mengsumsikan terdapat dua spesies yaitu anjing yang sehat dilambangkan S(t) dan anjing yang terinfeksi rabies dilambangkan R (t).
Pada bagian ini dibahas analisis kestabilan model yang digunakan dalam artikel ini. Langkah-langkah dalam menganalisis model yaitu menentukan titik-titik kesetimbangan pada model, melinierkan model dan menganalisis kestabilan model. Pada bagian akhir dibahas tentang simulasi numerik untuk memperkuat hasil analisis.
Sebelum masuk ke model matematika, dilihat tentang populasi anjing itu sendiri. Populasi anjing yang sehat bertambah karena adanya kelahiran dan berkurang karena selain adanya kematian juga karena tertular rabies. Anjing yang sehat dapat tertular rabies apabila ada interaksi (kontak) dengan anjing yang terinfeksi rabies. Proses penularan ini dapat dicegah dengan pemberian vaksin. Sehingga berkurangnya populasi anjing yang sehat bergantung terhadap persentase pemberian vaksin dan laju kematiannya. Populasi anjing sehat juga berkurang karena adanya eliminasi. Eliminasi dilakukan oleh pemeritah terhadap anjing yang sehat yang diduga akan tertular rabies. Jika anjing yang sehat belum diberi vaksin atau terlambat dalam pencegahan selama proses penularan berlangsung maka populasi anjing yang terinfeksi rabies akan bertambah dan berkurang karena adanya eliminasi. Penjelasan mengenai penularan rabies pada anjing dengan vaksinasi diilustrasikan dalam gambar berikut:
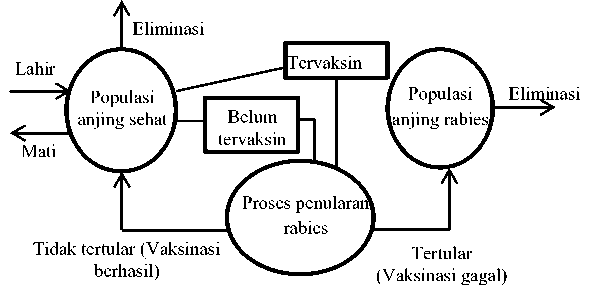
Gambar 2.Penjelasan Penularan Rabies pada Anjing dengan Vaksinasi
Dengan mengasumsikan terdapat dua kelompok yaitu anjing sehat dan anjing yang terinfeksi rabies maka model yang akan dirancang hampir sama dengan model interaksi antar dua spesies. Adapun asumsi lain dalam model yang dirancang yaitu sebagai berikut:
-
a. Anjing yang terinfeksi rabies tidak dapat disembuhkan.
-
b. Tidak ada migrasi anjing.
-
c. Laju kelahiran dan kematian dari anjing yang sehat maupun yang terinfeksi rabies adalah tetap.
-
d. Rabies pada anjing hanya ditularkan dari anjing yang terinfeksi rabies melalui interaksi.
Selanjutnya dimisalkan populasi anjing yang sehat bertambah akibat adanya kelahiran sebesar K (diasumsikan konstan), berkurangnya populasi anjing sehat akibat adanya kematian sebesar μS( t) dan tertular rabies akibat adanya interaksi (kontak fisik) dengan anjing yang terinfeksi rabies sebesar (1—m)βSS (t') R (t') dengan m adalah persentase pemberian vaksin. Adanya penularan rabies terhadap anjing yang sehat populasi anjing rabies akan bertambah. Kedua populasi tersebut juga berkurang karena adanya eliminasi masing-masing sebesar sS ( t) dan rR( t).
Penjelasan mengenai gambaran perancangan model matematika pada anjing rabies dengan vaksinasi dapat dilihat dalam gambar 3.
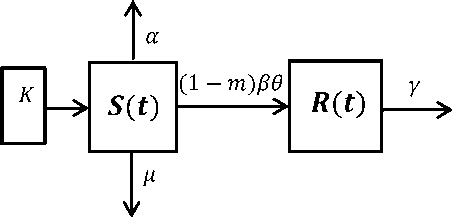
Gambar 3.Gambaran Perancangan Model Matematika pada Anjing Rabies dengan Vaksinasi.
Model lengkap akan menghasilkan sistem persamaan diferensial nonlinier berikut:
-
—r~ — K — μS — (1 — Tn) β θ SR — sS
at
(7)
dR _
-
— — (1 — m)βΘRR — rR
at
denganK,μ,β, θ,m,s,R > 0
-
S: adalah populasi dari anjing yang sehat
R: adalah populasi dari anjing yang terinfeksi rabies
K: adalah laju kelahiran dari anjing yang sehat (diasumsikan konstan) μ: adalah laju kematian dari anjing yang sehat
β: adalah laju anjing yang sehat dapat tertular rabies
θ: adalah laju interaksi antara anjing yang sehat dengan anjing yang terinfeksi rabies m: adalah persentase pemberian vaksin terhadap anjing yang sehat
-
a: adalah laju eliminasi terhadap populasi anjing yang sehat
γ: adalah laju eliminasi terhadap populasi anjing yang terinfeksi rabies
Nilai kesetimbangan model didapat jika ~~~) = ~^(^) = 0 (Brown, et. al. [3]).
Sehingga titik kesetimbangan pada model didapat pada saat
K — μS(t) — (1 — m)βθS)t)R)t) — aS(t) = 0
(1 — m)βθS)t)R)t) — RR(J) = 0
Didapat dua titik kesetimbangan pada sistem (7)
yaitu(S∙(t), R∙(t)) = {(i,0)⅛,~Z=^^
Titik kesetimbangan yang pertama yaitu TK1 = {(^,θ)} menjelaskan bahwa populasi anjing rabies akan mengalami kepunahan. Sedangkan pada titik kesetimbangan yang kedua yaitu TK2 = {(^^^(1-(^^ populasi anjing rabies
tergantung terhadap nilai parameter K,μ,β,θ,m,adan y. Karena titik kesetimbangan mempunyai nilai maka(1 — m)βθ ≠ 0. Hal ini dapat diartikan bahwa m ≠ 100%, dengan demikian tidak mungkin dilakukan pemberian vaksin terhadap seluruh populasi anjing yang belum terifeksi rabies. Parameter K dan m terkandung dalam titik kesetimbangan TK2j jika (1 — m)βθ — (μ + a)γ < 0 maka titik kesetimbangan TK2 bernilai negatif. Oleh karena populasi tidak bernilai negatif sehingga batas nilai
parameter K dan madalah K(1 — m≥ ≥ (^-^
.
Dengan melinierkan sistem (7) di dekat titik-titik kesetimbangan, dapat membantu dalam penentuan apakah titik kesetimbangan tersebut stabil atau tidak.Matriks jacobian untuk sistem (7) yaitu
M =
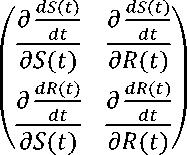
Jika matriks M dihitung pada titik kesetimbangan (S*(t),R*(t)) dari sistem (7) maka
—R-
- (1-m)βθR*(t)
(1-m)βθR*(t)
a -(1-m)βθS*(t) \
(1 - m') βΘS∖t) - γ)
Selanjutnya ditentukan matriks M pada titik kesetimbangan (S*(t),R*(t)) yang pertama yaitu KK= = {(“, 0)}, maka didapatkan matriks M berikut
-( + )
M —
(1 - m) βθK \ μ + a
(1 - )
μ + a γ /
Selanjutnya ditentukan matriks M pada titik kesetimbangan (S*(t),R*(t)) yang kedua yaitu TK2 = {(^~^^ >~^~m^^ maka didapatkan matriks M berikut
M = ( (+ + V + a) θγ)denganP = K(1 — m)βθ — (μ + α)γ
Pada bagian ini dianalisis kestabilan pada titik kesetimbangan sistem (7) yaitu pada titik kesetimbanga TK1 = {(~,θ)} dan
κo→nw→^n
-
2 t∖(l - m) β θ, (1 - m) β θ J)
Nilai karakteristik pada titik kesetimbangan TK1 = {(^,θ)} diberikan oleh
∣λl -MI =
λ + (μ + a')
—
0
(1 - m) βθ K
Hasil yang didapatkan yaitu
1 _ (1-m^θK
-
(8)
λ 1 — -(μ + a), λ = —-----;------
+
Kedua nilai λ berupa bilangan real, maka agar titik kesetimbangan TK1 = {(~,θ)} stabil haruslah kedua nilai karakteristik tersebut bernilai negatif.λ 1 < 0 karena μ + a > 0 maka λ2 — (~m~θθ~ - γ <0 sehingga nilai (1 - m)K < ^~^p~. Dengan demikian berdasarkan teori kestabilan pada titik kesetimbangan TK1 = {(^,0)} diperoleh jenis kestabilannya adalah stabil asimtotik.
Nilai karakteristik pada titik kesetimbangan TK2 = {((^γγf^ ,~(-^^ diberikan oleh
λ + (μ + P + a) y
-
λ
sehingga diperoleh persamaan karakteristik λ2 + (μ + P + α)λ + yP = 0 dengan demikian didapatkan
λ1,2 =
—(μ + P + α) ± √(μ + P + a22 — 4yP
(9)
2
Parameter K dan mterkandung dalam bagian akar (9).λ 1,2berupa bilangan real berbeda jika (μ + P + a22 — 4yP > 0 sehingga didapatkan (1 — m)< < (-a-γ- . Akan tetapi salah satu nilai karakteristik bernilai positif, sehingga menurut teori kestabilan pada keadaan ini sistem (7) tidak stabil. Jika (1 — m')= = ^~apγ^ maka λ1,2 berupa bilanga real dan sama sehingga sistem (7) stabil ke titik kesetimbangan T K2S Sedangkan jika (1 — m)> > (-a-γ maka bagian akar dari (9) berupa bilangan kompleks, sehingga nilai karakteristik λ berupa bilangan kompleks konjugat. Menurut teori kestabilan keadaan ini disebut fokus stabil dan sistem (7) stabil ke TK2.
Hasil yang didapatkan pada sistem (7) yaitu terdapat dua titik kesetimbangan antaranya titik kesetimbangan yang pertama yaitu TK1 = {(~,θ)} dengan pasangan (i -m)θθκ
— (μ + a) , —^^--y}. Titik kesetimbangan yang kedua
yaitu TK2 = {(∙
γ K (1 -m)βθ-+a+α)γ'
(1 - m) β θ,
(1 -m)θθ
■)} dengan pasangan nilai karakteristik λ 1 ,2 =
- (μ+P+a) ±√ (μ a P a a)2 - YγP
.
.
2
bergantung terhadap nilai
Analisis titik tetap menghasilkan dua keadaan yang
Kdan m. Jika (1 — m)< < (^+21 maka sistem (7) akan
stabil ke titik kesetimbangan TK1S Sedangkan jika(1 — m)> > (^+21 maka sistem (7) akan stabil ke titik kesetimbangan TK2a Agar populasi anjing rabies dapat dipunahkan maka haruslah sistem (7) stabil ke titik kesetimbangan yang pertama yaitu =
{(£, θ)}, sehingga(1 — m)K <
(P+a) Y βθ
Hasil analisis menguatkan bahwa tidak hanya nilai pesentase pemberian vaksin yang berpengaruh terhadap populasi anjing rabies. Populasi anjing rabies juga dipengaruhi oleh laju kelahiran anjing yang sehat, begitu juga sebaliknya. Jika nilai persentase pemberian vaksin tetap, misalkan m = m* maka batasan nilai dari laju kelahiran populasi anjing sehat agar populasi anjing rabies dapat punah yaitu < ^~a)γβθ. Sebaliknya, jika laju kelahiran dari populasi anjing sehat tetap per tahunnya,
misalkan K= ∗ per tahun, maka batas nilai persentase pemberian vaksin agar populasi
rabies punah adalah m>1
(μ+a)2 K∗βθ .
Simulasi yang dilakukan menggunakan metode Deret Taylor orde satu seperti yang tertulis dalam buku (Saxena [13]). Nilai-nilai parameter yang digunakan yaitu μ = 0.0002, β = 0.0011, θ = 0.014 , a = 0.008dan Y = 0.73. Kemudian diambil m = 87.18% , S(0) = 374500 dan R(0) =120 (sesuai dengan data yang didapat dari Dinas Peternakan dan Kesehatan Hewan Provinsi Bali) dengan demikian agar sistem (7) stabil, maka haruslah laju kelahiran dari populasi anjing sehat tidak lebih dari 3032 ekor per tahun, yaitu K < 3032. Akan tetapi untuk nilai K < 3032 pada sistem akan menghasilkan nilai P<0 sehingga titik kesetimbangan yang kedua (TK2 ) bernilai negatif tetapi sistem tidak stabil ke TK2 . Dengan mengambil nilai K = 2500 maka pada sistem (7) akan didapat nilai TK1 = (304878 ,0) dengan pasangan nilai karakteristik , =(-8.2×10 3,-0.1281). Karena kedua nilai karakteristik bernilai negatif maka
sistem (7) stabil ke titik kesetimbangan TK1 . Selanjutnya akan didapatkan =
(369755 ,-532)dengan pasangan nilai karakteristik , = (-0.0314 , 0.0243). Karena
salah satu nilai karakteristik bernilai positif, maka sistem (7) tidak akan stabil ke titik kesetimbangan TK2 . Salah satu titik kesetimbangan TK2 bernilai negatif, dimana jumlah populasi tidak bernilai negatif sehingga hanya terdapat satu titik kesetimbangan yang
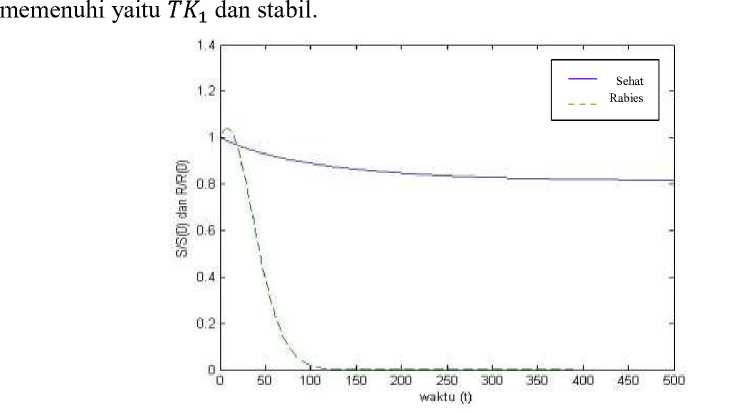
Gambar 4. Hasil simulasi sistem (7) dengan nilai parameter Vt- = 0.0002, β = 0.0011, =
0.014 , a = 0.008 , Y = 0.73 , S(0) = 374500, R(0) =120 , m = 87.18% danK = 2500.
Pada gambar 4 terlihat bahwa sistem (7) stabil ke TK1 dan R menurun menuju 0 atau populasi anjing rabies punah.
Selanjutnya dengan memperbesar laju kelahiran dari populasi anjing yang sehat menjadi K = 3100 maka pada sistem (7) akan didapatkan nilai TK1 = (378049 ,0) dengan pasangan nilai karakteristik , =(-8.2×10 3, 0.0164). Karena salah satu nilai karakteristik bernilai positif maka sistem (7) tidak stabil ke titik kesetimbangan TK1 . Kemudian akan didapatkan nilai TK2 = (369755 ,68) dengan pasangan nilai karakteristik , =(-4.16×10 3 ± 0.009i,). Karena nilai karakteristik berupa bilangan kompleks konjugat bagian realnya negatif, maka sistem (7) fokus stabil ke titik kesetimbangan TK2 . Dapat diartikan bahwa semakin besar laju kelahiran dari populasi anjing sehat yaitu melebihi 3032 ekor per tahun, maka jumlah populasi anjing rabies tetap eksis atau tidak dapat punah. Sehingga, jika pesentase pemberian vaksin pada populasi anjing sehat sebesar 87.18% agar populasi anjing rabies dapat punah maka batasan nilai laju kelahiran populasi anjing sehat tidak melebihi 3032 ekor per tahun.
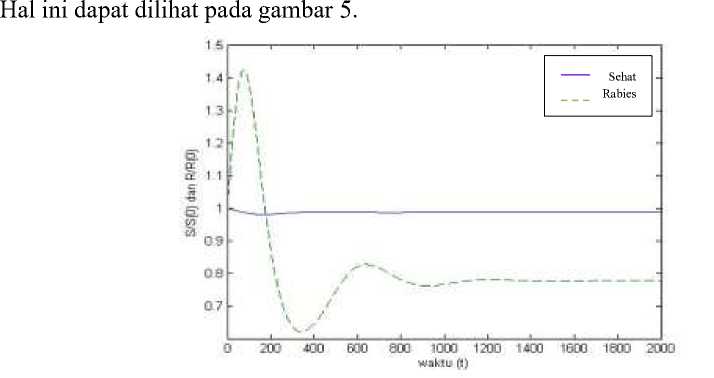
Gambar 5.Hasil Simulasi Persamaan (7) dengan Menggunakan Nilai K = 3100.
Pada gambar 5 terlihat bahwa sistem (7) stabil ke titik kesetimbangan TK2 . Populasi anjing rabies tetap eksis, sehingga laju kelahiran dari populasi anjing sehat juga berpengaruh terhadap jumlah populasi anjing rabies, yaitu tidak melebihi 3032 ekor per tahun.
Selanjutnya, dilihat pengaruh nilai persentase pemberian vaksin terhadap jumlah populasi anjing. Dengan mengasumsikan laju kelahiran populasi anjing sehat tetap sebesar 3000 ekor per tahun maka akan didapatkan batasan nilai persentase pemberian vaksin terhadap populasi anjing sehat yaitu m > 87.04% per tahun. Dengan mengambil m=88% pada sistem (7) dihasilkan nilai TK1 = (365854 ,0) dengan pasangan nilai karakteristik , =(-8.2×10 3,-0.0539). Karena kedua nilai karakteristik bernilai negatif maka sistem (7) stabil ke titik kesetimbangan TK1 . Selanjutnya didapatkan TK2 = (395022 , -239) salah satu titik kesetimbangan bernilai negatif, dimana jumlah populasi tidak bernilai negatif sehingga sistem tidak stabil ke titik kesetimbangan TK2 .
Dari hal tersebut maka hanya terdapat satu titik kesetimbangan yang memenuhi yaitu TK1 dan stabil. Hasil simulasi lebih jelah dapat dilihat pada gambar 6.
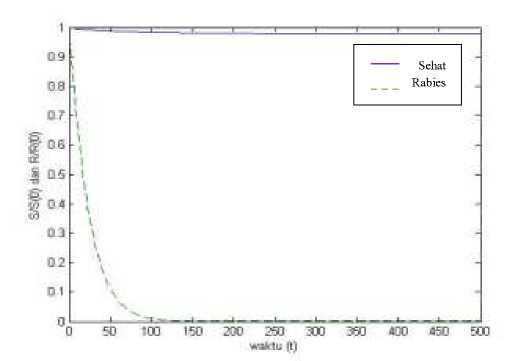
Gambar 6. Hasil simulasi persamaan (7) dengan nilai parameter Vt- = 0.0002, =
0.0011, θ = 0.014, a = 0.008, Y = 0.73, R(0) = 120, S(0) = 374500 , =
3000 dan m = 88%.
Pada gambar 6 terlihat bahwa sistem (7) stabil ke TK1 dan R menurun menuju 0 atau populasi anjing rabies dapat punah.
Dengan memperkecil nilai pemberian vaksin terhadap populasi anjing sehat menjadi m=70% maka pada sistem (7) didapatkan nilai TK1 = (365854 ,0) dengan pasangan nilai karakteristik , =(-8.2×10 3, 0.9602). Karena salah satu nilai
karakteristik bernilai positif maka sistem (7) tidak stabil ke titik kesetimbangan TK1 . Kemudian didapatkan nilai TK2 = (158009 , 1704) dengan pasangan nilai karakteristi , =(-8.04×10 3 ± 0.0758i). Karena nilai karakteristik berupa
bilangan kompleks konjugat dengan bagian realnya negatif, maka sistem (7) fokus stabil ke titik kesetimbangan TK2 . Hal ini dapat diartikan bahwa semakin kecil nilai persentase pemberian vaksin terhadap populasi anjing sehat yaitu kurang dari 70%, maka populasi anjing rabies tetap eksis dan meningkat. Sehingga, jika laju kelahiran populasi anjing sehat sebesar 3000 per tahun, agar populasi anjing rabies dapat punah maka batasan nilai persentase pemberian vaksin mesti lebih dari 87.04% per tahun (gambar 7).
Gambar 7 memperlihatkan bahwa sistem (7) stabil ke TK2 . Sehingga besar kecilnya nilai pemberian vaksin terhadap populasi anjing sehat berpengaruh terhadap jumlah populasi anjing rabies, yaitu tidak kurang dari 87.04% per tahun.
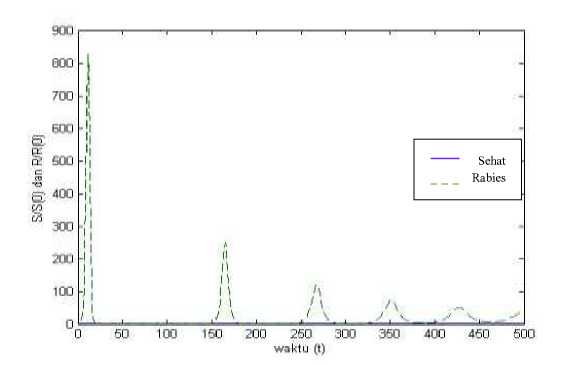
Gambar 7.Hasil Simulasi Persamaan (7) dengan Menggunakan Nilai m = 70%.
Pada bagian selanjutnya akan dilihat pengaruh eliminasi terhadap jumlah populasi anjing rabies. Dengan menggunakan nilai-nilai parameter μ = 0.0002, =
0.0011, θ = 0.014 , a = 0.008 , S(0) = 374500, R(0) =120 , K = 2500 dan =
-
8 7.18% kemudian laju eliminasinya diperbesar menjadi Y = 0.99, maka pada sistem (7) akan didapat nilai TK1 = (304878 ,0) dengan pasangan nilai karakteristik , =(-8.2×
-
10 3,-0.3881). Jika nilai Y diperkecil dari sebelumnya, dalam artian laju eliminasinya dikurangi menjadi Y = 0.64, maka pada sistem (7) akan didapat nilai =
(304878 ,0) dengan pasangan nilai karakteristik , =(-8.2×10 3, -0.0381). Karena
kedua nilai karakteristik bernilai negatif maka sistem (7) stabil ke titik kesetimbangan TK1 untuk Y = 0.99 ataupun Y = 0.64. Hal ini dapat diartikan bahwa laju eliminasi tidak berpengaruh terhadap kestabilan sistem, akan tetapi laju eliminasi dapat mempercepat kepunahan populasi anjing rabies. Semakin besar laju eliminasinya, maka
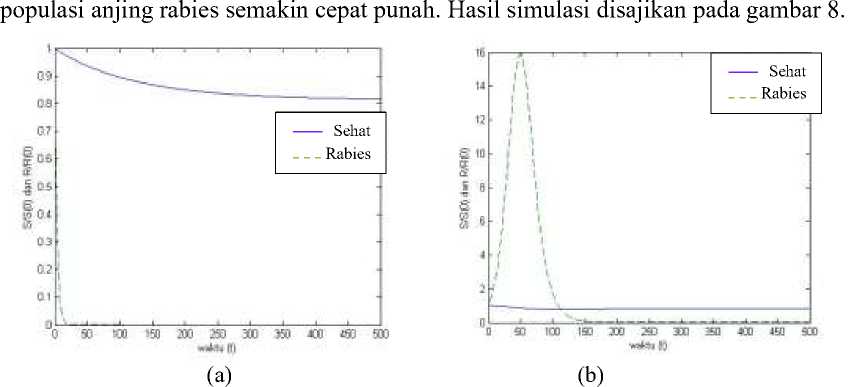
Gambar 8. Hasil simulasi persamaan (7) dengan menggunakan nilai Y = 0.99 pada bagian (a) dan Y = 0.64 pada bagian (b).
Terlihat bahwa sistem (7) stabil keTK1 dan pada (a) populasi anjing rabies cepat punah dibandingkan yang (b). Sehingga besar kecilnya nilai eliminasi dapat berbengaruh terhadap percepatan kepunahan populasi anjing rabies.
Hasil analitik menegaskan bahwa tidak hanya nilai persentase pemberian vaksin yang berpengaruh terhadap jumlah populasi anjing rabies, melainkan laju kelahiran dari populasi anjing sehat juga dapat berpengaruh terhadap jumlah poulasi anjing rabies. Populasi anjing rabies akan punah jika laju kelahiran dari populasi anjing sehat tidak melebihi 3032 ekor per tahun, dengan ketentuan nilai pemberian vaksin lebih atau sama dengan 87.18%. Begitu juga sebaliknya, jika laju kelahiran dari populasi anjing sehat tetap yaitu 3000 ekor per tahun maka populasi anjing rabies menurun jika nilai pemberian vaksin tidak kurang dari 87.04%.
Model matematika (nonlinier) pada populasi anjing rabies dengan vaksinasi mempunyai bentuk = - μS-(1-m)βθSR - aS ,H=(1-m)βθSR - γR
model ini stabil untuk setiap nilai m dan K, akan tetapi populasi anjing rabies dapat punah jika (1-m)K<(μ+a )- = 388.7. Jika K = 3000 per tahun maka m > 87.04% begitu juga sebaliknya, jika m = 87.18% maka K < 3032 ekor per tahun. Dapat diartikan jika suatu daerah terkena rabies, maka tidak hanya nilai persentase pemberian vaksin yang berpengaruh terhadap jumlah populasi rabies, melainkan jumlah kelahiran dari populasi yang belum terinfeksi juga berpengaruh, begitu juga sebaliknya.
Saran
Model ini perlu dikembangkan dengan memperhatikan faktor-faktor lainnya seperti pengelompokan jenis-jenis anjing, yaitu anjing yang rentan terinfeksi rabies (anjing liar) dan yang tidak mudah terinfeksi rabies (anjing rumahan) ditinjau dari tingkat interaksi antara anjing sehat dengan anjing rabies. Model tersebut terdiri dari empat sistem persamaan diferensial.
Daftar Pustaka
-
[1] Anton, H., & Rorres, C. 2004. Aljabar Linier Elementer, Versi Aplikasi Edisi Kedelapan. Jakarta: Erlangga.
-
[2] Besung, INK K., At all. 2011. Vaksinasi, Edukasi dan Eliminasi Anjing Liar Sebagai Usaha Percepatan Penanggulangan Penyakit Rabies di Bali. Udayana Mengabdi, 57-60.
-
[3] Brown, R., Clements, D., & Widana, I. N. 1994. Catatan Kuliah Persamaan Diferensial. Indonesia Australia: AIDAB.
-
[4] Burghes, D., & Borrie, M. 1981. Modeling with Differential Equations.
Chichester: Ellis Horwood Limited.
-
[5] Cronin, J. 1994. Differential Equations Introduction and Qualitative Theory. Second Edition, Revised and Expanded. New York: Marcel Dekker, INC.
-
[6] Edwards, C., & Penny, D. E. 1993. Elementary Differential Equations with Boundary Value Problems Third Edition. New Jersey: Prentice-Hall, Inc.
-
[7] Fitri, A., Oka, T. B., & Widana, I. N. 2014. Model Matematika (Linier) Populasi Anjing Rabies dengan Vaksinasi. Jurnal Matematika Vol 4. No 2, 70-79.
-
[8] Lucas, W. F. 1983. Differential Equation Model. New York: Springer-Verlag.
-
[9] Nugroho, D. K., & Rahayujati, T. B. 2013. Analisa Data Surveilans Rabies (20082011) di Propinsi Bali, Indonesia. Outbreak, Surveillance and Investigation Reports, 8-12.
-
[10] Putra, A.A.G. 2011. Epidemiologi Rabies di Bali: Analisis Kasus Rabies "Semi free- Ranging Dog" dan Signifikasinya Dalam Siklus Penularan Rabies dengan Pendekatan Ekosistem. Buletin Veteriner, BBVet Denpasar, 45-54.
-
[11] Putra, A.A.G. 2012. Analisis Perkembangan Pemberantasan Rabies di Provinsi Bali: Capaian Pasca Vaksinasi Massal ke Tiga. Buletin Veteriner, BBVet Denpasar, 10-22.
-
[12] Rumlawang, F., & Nanlohy, M. I. 2011. Analisis Kestabilan Model Penyebaran Penyakit Rabies. Jurnal Barekang Vol. 5 No. 2, 39-44.
-
[13] Saxena, H. 2008. Finite Differences and Numerical Analysis. New Delhi: S. Chand & Company Ltd.
-
[14] Wang, X., & Lou, J. 2008. Two Dynamic Models About Rabies Between Dogs and Human. Journal of Biological System, Vol. 16, No. 4, 519-529.
29
Discussion and feedback