Analisis Sensitivitas Pada Model Matematika Penyebaran Penyakit Demam Dengue dengan Laju Insidensi NonLinier

Jurnal Matematika Vol. 12, No.2, Desember 2022, pp. 127-143

Article DOI: 10.24843/JMAT.2022.v12.i02.p155

ISSN: 1693-1394

Analisis Sensitivitas Pada Model Matematika Penyebaran Penyakit Demam Dengue dengan Laju Insidensi NonLinier

I Putu Winada Gautama

Program Studi Matematika, Universitas Udayana e-mail: [email protected]

Ni Kadek Nova Anggarani

Program Studi Fisika, Universitas Udayana e-mail: [email protected]

I Made Eka Dwipayana

Program Studi Matematika, Universitas Udayana e-mail: [email protected]

Putu Veri Swastika

Program Studi Matematika, Universitas Udayana e-mail: [email protected]

Abstract: Dengue fever can result in death if not treated seriously. This disease is transmitted to humans through the Aedes aegypti mosquito, the Aedes albopictus mosquito, and other species of the Aedes genus. The mechanism of dengue fever transmission can be understood through appropriate mathematical models. In general, parameter values for modeling the spread of disease are very uncertain because there is no data regarding these parameters. On the other hand, parameter values greatly influence the prediction accuracy of a mathematical model. Uncertainty analysis to determine these parameters uses sensitivity analysis. This study found that the bite rate of susceptible and infected mosquitoes (b') and the mosquito death rate (μ_v) have a large influence on changes in the value of R₀. Human recovery rate (r), mosquito mortality rate (μ_v), and human mortality rate (μ_li) have a ma jor influence on infected human individuals (I_h). The bite rate of susceptible and infected mosquitoes (b) has the most positive influence on the number of infected mosquitoes I_v. The mortality rate of μ_v mosquitoes had the most negative relationship with the number of mosquitoes infected with I_v. Numerical simulations are carried out to determine the dynamics that occur when parameter values are increased or decreased.

Keywords: Sensitivity Analysis, Dengue Fever, Mathematical Modeling

Abstrak: Demam berdarah dapat mengakibatkan kematian jika tidak ditangani dengan serius. Penyakit ini menular ke manusia melalui nyamuk Aedes aegypti, nyamuk Aedes albopictus, dan spesies lain dari genus Aedes. Mekanisme penularan demam berdarah dapat dipahami melalui model matematika yang tepat. Secara umum nilai parameter

untuk pemodelan penyebaran penyakit sangat tidak pasti karena belum adanya data mengenai parameter tersebut. Di sisi lain, nilai parameter sangat memengaruhi keakuratan prediksi suatu model matematika. Analisis ketidakpastian untuk menentukan parameter tersebut menggunakan analisis sensitivitas. Pada penelitian ini diperoleh tingkat gigitan nyamuk rentan dan terinfeksi (S) dan laju kematian nyamuk (μ_v) memiliki pengaruh yang besar terhadap perubahan nilai R₀. Laju kesembuhan manusia (r'), laju kematian nyamuk (μ_v), laju kematian manusia (μ_H) memiliki pengaruh besar terhadap individu manusia yang terinfeksi (I_h) . Tingkat gigitan nyamuk rentan dan terin feksi b memiliki pengaruh paling positif dengan jumlah nyamuk yang terinfeksi I_v. Laju kematian nyamuk μ_v memiliki hubungan paling negatif dengan j'umlah nyamuk yang terinfeksi I_v. Simulasi numerik dilakukan untuk mengetahui dinamika yang terjadi apabila nilai parameter tersebut dinaikkan atau diturunkan.

Kata kunci: Analisis Sensitivitas, Demam Dengue, Pemodelan Matematika

• 1.    Pendahuluan

Penyakit demam berdarah Dengue sudah banyak mewabah di Dunia. Berdasarkan data WHO lebih dari 100 negara bagian WHO yang menjadi endemik penyakit ini. Lebih dari 2000 kasus di pulau Madeira di Portugal terjangkit wabah demam berdarah sekitar tahun 2010. Pada tahun 2010 pertama kali dilaporkan terjadi penularan lokal di Perancis dan Kroasia. Pada tahun 2016, lebih dari 3,34 juta kasus tersebar di Amerika, Asia Tenggara, dan Pasifik Barat. Wabah demam berdarah terbesar terjadi pada tahun 2016, 2,38 juta kasus di Amerika, 176.411 di Filipina, lebih 375.000 kasus di wilayah pasifik barat, 100.028 kasus di Malaysia, dan 1061 kasus di Afrika tepatnya Burkina Faso. Selanjutnya terjadi pengurangan kasus yang signifikan pada tahun 2017 yaitu sebasar 73% yang terjadi di Amerika. Namun sebaliknya, terjadi peningkatan jumlah kasus di negara Panama, Peru, dan Aruba (WHO, 2012).

Demam berdarah dengue endemik di daerah yang beriklim tropis. Dikombinasikan dengan tren global ini, peningkatan suhu yang disebabkan oleh perubahan iklim telah meningkatkan kekhawatiran bahwa demam berdarah akan meningkat di daerah yang sudah endemis melalui penularan virus yang lebih cepat, peningkatan kelangsungan hidup vektor, reproduksi dan laju gigitan, yang pada akhirnya menyebabkan musim penularan lebih lama dan lebih banyak korban jiwa (Messina dkk., 2019).

Angka kematian akibat demam berdarah parah memang rendah, namun beban ekonomi dan sumber daya terhadap layanan kesehatan masih besar di wilayah endemik (Wilder-Smith dkk., 2019). Demam berdarah dengue dapat berakibat kematian apabila tidak ditangani secara serius. Komplikasi yang hebat terkait dengan pendarahan, kerusakan organ, dan kebocoran plasma. Beberapa ciri - ciri umum gejala demam berdarah seperti suhu badan yang tinggi, sakit kepala berat, nyeri pada sendi, nafsu makan berkurang,

mual, muntah, dan ruam kemerahan (WHO, 2012). Belum ada pengobatan khusus untuk infeksi demam berdarah. Namun, perawatan medis yang tepat bisa menyelamatkan nyawa pasien (Pathak & Mohan, 2019; Rosmalena dkk., 2019). Tidak adanya pengobatan antivirus yang spesifik dan vaksin berlisensi menimbulkan kekhawatiran atas peningkatan risiko rawat inap akibat efek ketergantungan antibodi (Jing & Wang, 2019).

Demam berdarah adalah infeksi flavivirus yang ditularkan oleh nyamuk, terutama ditularkan oleh Aedes aegypti diikuti oleh nyamuk Aedes albopictus dan spesies lain dari genus Aedes (Mutheneni dkk., 2017; Pereira dkk., 2020). Virus ini ditularkan melalui gigitan nyamuk betina Aedes yang terinfeksi (Eivazzadeh-Keihan dkk., 2019). Ada empat serotipe virus dengue yang berbeda secara antigen yaitu DENV-1, DENV-2, DENV-3, dan DENV-4 (Bhatt dkk., 2021; Saxena dkk., 2019). Pada manusia, infeksi DENV menyebabkan dengue fever (DF) dan pada kasus yang parah dengue hemorrhagic fever (DHF) atau dengue shock syndrome (DSS). Dalam siklus penularan, setelah disuntikkan ke dalam tubuh manusia, virus memasuki sel inang, membajak mesin sel inang untuk bereplikasi, dan lolos dari strategi kekebalan inang untuk menimbulkan gejala patologi (Mukherjee dkk., 2019). Diantara keempat serotipe virus dengue, DENV-1 dan DENV-2 yang paling sering dilaporkan menginfeksi manusia (Guo dkk., 2017; Mwanyika dkk., 2021). Meskipun serotipe DENV mempunyai kesamaan sekitar 65%, infeksi dengan serotipe yang berbeda menunjukkan serangkaian gejala klinis(Nanaware dkk., 2021). Faktanya bahwa orang terinfeksi virus dengue memiliki kekebalan terhadap serotipe tertentu pasca pemulihan. Namun, kekebalan silang terhadap serotipe lain setelah pemulihan hanya sementara dan sebagian, dimana infeksi sekunder oleh serotipe lain meningkatkan risiko terkena demam berdarah yang lebih parah (Biswas dkk., 2021). Biasanya terjadi kasus, manusia yang terinfeksi virus ini kemudian melakukan perjalanan ke daerah atau negara lain, kemudian apabila ada vektor rentan di daerah baru tersebut, maka kemungkinan akan ada potensi untuk terjadinya transmisi lokal. Demam berdarah dapat terjadi pada pelancong wisata, pelancong bisnis dan patriat, migran dan mereka yang mengunjungi teman dan kerabat, pekerja asing dan peziarah, baik pada pelancong dewasa maupun anak-anak(Halstead & Wilder-Smith, 2019).

Model matematika yang tepat dapat memberikan wawasan mengenai penularan penyakit demam dengue. Pada umumnya nilai parameter dari suatu pemodelan penyebaran penyakit sangat tidak pasti karena tidak adanya data mengenai parameter tersebut. Dilain pihak, keakuratan prediksi dari model matematika sangat dipengaruhi oleh nilai dari parameter (Chitnis dkk., 2008). Oleh karena itu, diperlukan suatu analisis untuk menentukan parameter yang berpengaruh dalam model matematika tersebut. Analisis yang digunakan untuk menentukan nilai parameter tersebut adalah analisis sensitivitas. Pada artikel ini akan difokuskan pada analisis sensitivitas pada model penyebaran penyakit demam berdarah dengue terhadap bilangan reproduksi dasar dan titik

kesetimbangan endemik, sehingga bertujuan untuk mengetahui parameter yang paling berpengaruh pada model matematika ini.

• 2.    Metode Penelitian

Pada bagian ini disajikan metode yang digunakan untuk menganalisis penyebaran demam dengue dan kemudian menyelidiki parameter yang berpengaruh. Pertama, dibentuk model penularan demam dengue antara populasi manusia dan populasi nyamuk berdasarkan fakta dan asumsi yang dikumpulkan. Kedua, menentukan solusi ekuilibrium dari model yang dibentuk. Ketiga, disajikan analisis sensitivitas parameter, yang digunakan untuk menentukan parameter mana yang paling memengaruhi jumlah kumulatif infeksi pada manusia. Keempat, melakukan simulasi numerik untuk melihat dinamika parameter dari model yang dibentuk.

Analisis sensitivitas memberikan gambaran parameter yang berpengaruh pada model yang dibentuk. Normalized Sensitivity Index dari variabel V, terdiferensialkan pada parameter p, didefinisikan sebagai berikut :

’-   ₇P

^Lp = dp × V

Dimana V adalah variabel yang akan dianalisis dan p adalah parameter ((Chitnis dkk., 2008).

• 3.    Hasil dan Pembahasan

• 3 .1 Formulasi Model Penyebaran Penyakit Demam Dengue dengan Laju Insidensi Nonlinear

Pembentukan model matematika pada penelitian ini menggunakan beberapa asumsi untuk penyederhaan model, yaitu

• 1.    Laju kelahiran dan laju kematian manusia dianggap sama (μ_κ). Angka rekruitmen nyamuk rentan dilambangkan dengan (4), sedangkan laju kematian nyamuk dilambangkan dengan (μ^).

• 2.    Kelahiran pada populasi manusia dan nyamuk pada masing-masing kelasnya masuk dalam kelas rentan.

• 3.    Setiap individu memiliki kemungkinan yang sama untuk tergigit nyamuk.

• 4.    Individu yang terinfeksi oleh satu serotipe virus bisa sembuh dan tidak akan terinfeksi oleh serotipe lainnya.

  5.

  
  

Laju insidensi penyakit untuk populasi manusia merupakan laju insidensi jenuh

bβHS_i{lv

1 + (Xly ,

sedangkan untuk nyamuk adalah laju insidensi bilinear bβ_vI_HS_v.

• 6 . Tingkat gigitan nyamuk terinfeksi dengan nyamuk rentan sama.

Variabel yang digunakan pada penelitian ini disajikan pada Tabel 1.

Tabel 1. Variabel pada Model Matematika Penyebaran Penyakit Demam Dengue dengan Laju Insidensi NonLinier

Variabel	Keterangan
Sh	kelas individu rentan
Eh	kelas individu yang sudah terinfeksi namun belum memiliki kemampuan menularkan virus dengue
Ih	kelas individu yang terinfeksi dan memiiki kemampuan untuk menularkan virus dengue
Eh	kelas individu yang telah sembuh dari infeksi
sv	kelas nyamuk yang rentan tertular virus dengue
Ev	kelas nyamuk yang terinfeksi namun belum dapat menularkan virus dengue
Iv	kelas nyamuk yang terinfeksi dan memiliki kemampuan untuk menularkan penyakit dilambangkan dengan

Berikut ini disajikan parameter yang digunakan dalam penelitian ini.

Tabel 2. Parameter pada Model Matematika Penyebaran Penyakit Demam Dengue dengan Laju Insidensi NonLinier

Parameter	Keterangan	Nilai	Sumber
Ph	peluang penyebaran virus dari Iv ke sh .	0.75	Asumsi
Pv	peluang penyebaran virus dari Ih ke Sv .	1	Asumsi
Hh	laju kelahiran dan kematian manusia.	3,91.10-5/ hari	(Pongsumpun, 2008)
Hv	laju kelahiran dan kematian nyamuk.	2,78.10-2/hari	(Pongsumpun, 2008)
a	ukuran efek penghambatan dari perubahan tingkah laku yang dilakukan oleh individu yang rentan	10-5	Asumsi
'b	Tingkat gigitan nyamuk rentan dan nyamuk terinfeksi.	0,5	Asumsi
r	laju kesembuhan individu.	0,125	(Pongsumpun, 2008)
Yh	laju manusia yang baru terinfeksi akan menjadi manusia yang mampu menularkan virus dengue	0,1667	(WHO, 2012)
Yv	laju nyamuk yang baru terinfeksi akan menjadi nyamuk yang mampu menularkan virus dengue	0,147	(WHO, 2012)

Berikut diagram transfer Model Matematika Penyebaran Penyakit Demam Dengue dengan laju insidensi nonlinear.

Gambar 1. Diagram model penyebaran penyakit dengue dengan masa laju insidensi nonliner.

Berdasarkan Gambar 1, diperoleh sistem sebagai berikut:

dSH dt	bβHsH1v ~μ"κ  1 + alv  -  '
dEH dt	_ bβHsH1V =          (eH + YhJeH 1 + alv
dlH dt	= YHEH - rlH - E-H1H
dR dt	= rlH - Ehrh
dSv dt	= A- bβvlHSv — EvSv
dEv dt	= bβvlHSv — YvEv — EvEv
dlv dt	= yvev - eviv

(1)

Dengan kondisi N_h = S_h + E_h + I_h + R_h dan N_v = S_v + E_v + I_v.

Dapat diperhatikan bahwa: dNv   dSv dEv dlv   .       ,,

(2)

~--^ ⁺ ~ ⁺ ~^~^A~^VvNv.

Dengan kondisi awal N_v(l₀) = N_vq ≥ 0, diperoleh solusi persamaan (2) sebagai berikut

N_v(t) = —— (—— N(t₀) ) e^μv(⁰~^tt dan lim N_v(t) = —. Oleh karena itu, diperoleh Mv    Vv                        t→∞         Vv

^SV ^{+ E}v ^{+ 1}V = ~∙

Vv

^SV = ~   ^(EV ^{+ 1}V)

Vv

Selanjutnya dapat diperhatikan

^^+^+^+I^PHV-^-

(4)

Dengan kondisi awal N_h(I₀) = N_h0 ≥ 0. Diperoleh solusi persamaan (4) N_h (t) = K-(K — N_H(t₀)')e^μ(t'^0-t dan lim N_H(t) = K. Sehingga diperoleh '            t→∞

^NH = ^SH ^{+ E}H ^{+ l}H ^{+ R}H = ^K.

^h = ^{K - (S}h + Eh⁺ IH)                      ⁽⁵⁾

Berdasarkan Persamaan (3) dan (5) Sistem (1) dapat direduksi menjadi

^dSH _      bβHSHly

~7~ = P-h^{k -} VTTT   ^pH^sH

at          1 + al_v

dE_H dt

^bβH^sH^lv

1 + alv

⁽Ph ⁺Yh)^eh

(6)

dlH

~^ = Yh^eh ^-rlH^{- p}H^lH

dE_v

= ^bβv^lHEv ^- Yv^ev ^{- p}v^Ev

dly

~^ = ^yv^ev ^{- p}v^lv

yang memiliki domain Ω = {(S_h, E_h, l_H, E, ly) G R+'-0 ≤ E_v + l_v ≤ — ,0 ≤ S_h + E_h + _μv

Ih ≤ K,Sh(0) ≥ 0,Eh(0) ≥ 0,1h(0) ≥ 0,Ev(0) ≥ 0,lv(0) ≥ 0}.

• 3.2    Eksistensi Titik Ekuilibrium

  Diberikan bilangan reproduksi dasar R₀ =

  
  

  ^k1PvPhYhYv^aK (YH+μH)(^r+μH)(Yv+μv')μV

  
  

  Penentuan

  
  

bilangan reproduksi dasar dengan menggunakan metode Next Generation Matrix (Van den Driessche & Watmough, 2002).

• 1.    JikaR₀ ≤ 1, maka Sistem (6) mempunyai titik ekuilibrium bebas penyakit E₁ = (K,O,O,O,O)

• 2.    Jika R₀ > 1, maka Sistem (6) mempunyai titik ekuilibrium endemik E₂ = (Sh,eh,ih,ev,iv)

Bukti :

Sistem (6) disamakan dengan nol diperoleh:

ΓA^YH^b^H^^pH^K    2²β β KI   ^YH^b2βV^βH^pH^KpV ^

• I.    Pv           ^{h h v h v}          γv V

  _-

  
  

  ((^bβH ^{+ ap}H)^lv ^{+ p}H)(^pH ^{+ γ}H)(^{r + p}H)(^γv ^{+ p}v^)pv Yv

  
  

  ■]^lv

  
  

  = 0 (7)

  
  

  IH

  
  

  SH

  
  

  μHK(1 + aIV) ^μH ⁺ (^sβH ^{+ aμ}H)¹V

  
  

  EH

  
  

  ^(r + ^μHVH

  
  

  ^μH^μV^(R0

  
  

  -

  
  

  Yh

  ¹)(∕v ^{+ μ}v)^μv

  
  

  bβv((bβH ^{+ aμ}H^^^γV ^{+ μ}H(^γV ^{+ μ}v)^μv) p * _ ^μvⁱv ^eV —

  Yv

  
  

  (8)

  (9)

  (10)

  (11)

  
  

Perhatikan, pada persamaan (7) diperoleh:

• 1.    Iv — 0

2∣* _ μH⁽μH⁺YH)^(r+μH)μv^(R0^-1)                                        (12)

. ^v   YHb²βHβvμHK+(bβH+aμH)(μH+YH)(r+μH)μv

Jika I_v — 0, maka diperoleh S_h — K, E_h — 0, I_h — 0, E_v — 0.

Jika R₀ ≤ 1, maka dari persamaan (8)-(12) diperoleh S_h — K, E_h — 0,I_h — 0,E_v — 0, dan I_v — 0

Jika R₀ > 1, diperoleh titik ekuilibrium E₂ — (S_π,E_ll,Γ_ll,E_v,,I_v,).

• 3.3    Analisis Sensitivitas

Pada penelitian ini akan dilakukan analisis sensitivitas dari parameter-parameter terhadap bilangan reproduksi dasar dan titik ekuilibrium endemik. Nilai parameter yang digunakan ditampilkan pada Tabel 1. β_Hβ_V,A,K,danab — 0,5;r — 0,125;γ_H — 0,1667; γ_v — 0,147.

• 3.3.1    Analisis Sensitivitas Terhadap R₀ dan Titik Ekuilibrium Endemik

Pada bagian ini dilakukan analisis sensitivitas terhadap R₀. Indeks sensitivitas untuk salah satu parameter yaitu, μ_v terhadap R₀ diperoleh sebagai berikut

I^R0 =

^Iμv

∂R0 μv -4μv + (-3r - 3γv)μv — ^2rYv

^dμv ^R0

⁽r + μv)(Yv + ^μv)

Kemudian nilai parameter disubstitusikan ke persamaan tersebut, diperoleh nilai seperti pada Tabel 3.

Berdasarkan Tabel 3, bahwa tingkat gigitan nyamuk rentan dan terinfeksi (S) dan laju kematian nyamuk (μ_v) memiliki pengaruh yang besar terhadap perubahan nilai R₀. Tingkat gigitan nyamuk memiliki hubungan yang positif, sedangkan laju kematian nyamuk memiliki hubungan yang negatif. Kenaikan nilai parameter (S) mengakibatkan

nilai R₀ juga mengalami kenaikan,berlaku, sedangkan kenaikan nilai parameter μ_v mengakibatkan nilai R₀ turun, berlaku juga sebaliknya.

Tabel 3. Indeks Sensitivitas terhadap R₀

Parameter	Persamaan	Nilai	Ro = 3.4067
			P-5%	P+5%
r	r r + μv	-0.8132726090	3.551150805	3.273630423
i	2	2	3.074590179	3.577085527
P-v	-4μv + (-3r - 3γv)μv - 2rγv (r + μv)(,Yv + Pv)	-2.350074005	3.841741915	3.036637033
Ph	μH Yh+Ph	-0.2344980871e-3	3.406788065	3.406708177
Yv	μv Yv + Pv	0.1633466135	3.377709311	3.433454941
Yh	μH Yh+Ph	0.2344980871e-3	3.406706075	3.406786163
Pv	1	1	3.236410715	3.577085527
Ph	1	1	3.236410715	3.577085527

Selanjutnya dilakukan analisis sensitivitas terhadap IH. Indeks sensitivitas untuk parameter β_v terhadap I_h diperoleh sebagai berikut:

/H =∂lHH-βv

^βv   ∂βv Ih

_____________________(.Yh + HnXr + Pv⁾⁽Yv + Pv)PvK____________________

• ^-K(Yh ⁺ ⅛)μv ^{- k(}Yh ⁺ Vh×Yv ⁺ r)μv ^- Yv^Kr(Yn ⁺ Ph)Pv ⁺ K²PhPvYhYvA Substitusikan nilai parameter berikut  P_h = 0,75; P_v = 1; μ_n = 3,91.10^-5; μ_v =

• 2,    78.10^-v;A = 1100; K = 400000; a = 10^-5; b = 0,5; r = 0,125; y_h =

0,1667; γ_v = 0,147, sehingga diperoleh nilai 0.4154984030. Hasil yang lengkap ditunjukkan pada Tabel 4.

Berdasarkan Tabel 4, bahwa laju kesembuhan manusia (r), laju kematian nyamuk (μ_v), laju kematian manusia (p_h) memiliki pengaruh besar terhadap individu manusia yang terinfeksi (I_h). Laju kesembuhan manusia (r) memiliki hubungan yang negatif dengan I_h , artinya kenaikan laju kesembuhan manusia (r), berdampak pada menurunnya jumlah manusia yang terinfeksi (I_h) . Hubungan negatif terjadi pada μ_v dengan I_h artinya, semakin naik nilai μ_v, maka nilai I_h semakin turun. Selanjutnya, μ_n memiliki hubungan yang positif dengan I_h , artinya semakin naik μ_n, maka nilai I_h semakin turun.

Analisis Sensitivitas terhadap IV diperoleh sebagai berikut :

jIv _ ^¹V ^γv _ __________________________________^y^ ^μv^pH ^pv^Ab2^YH__________________________________

^γv   ∂Yv Iv   ⁽Yv ⁺ μv×^-κ(Yn ⁺ Ph)Pv ^{- K(}Yv ^{+ r)(}Yn ⁺ Ph^Pv ^- Yv^Kr(Yn ⁺ Ph)Pv + ^bVpH^pvYnYv^A)

Substitusikan nilai parameter    β_H = 0,75; β_v = 1;μ_H = 3,91.10 ⁵; μ_v =

• 2,    78.0^-2M = 1100; K = 400000; a = 10^-5; b = 0,5; r = 0,125; y_H = 0,1667; γ_v = 0,147 diperoleh nilai 0.2312168706.

Tabel 4. Indeks Sensitivitas terhadap IH

Parameter	Nilai	Ih = 71.74742257
		P-5%	P+5%
r	-1.151186079	76.05220224	67.77905893
g	0.8327115424	68.52066621	74.52504644
Mk	-1.164689859	75.83653576	67.47882151
Mh	0.9979533313	68.1670271	75.3270851
Xk	0.06808234396	71.49033424	71.98003123
Xh	0.0003319316678	71.74616915	71.74855664
βv	0.4154984030	70.17842575	73.16699111
βH	0.4172131402	70.17209277	73.17296599

Indeks sensitivitas untuk parameter lainnya disajikan pada Tabel 5.

Tabel 5. Indeks Sensitivitas terhadap IV

Parameter	Nilai	Iv = 99.79230322
		P-5%	P+5%
r	-1.145773027	105.7496227	94.29707868
g	1.825996696	90.56976333	108.8022413
Mv	-3.321111254	117.7951169	84.46796603
Mh	0.9938416504	94.83188869	104.7496644
Xv	0.2312168706	98.58825131	100.8996626
Xh	0.0003306619201	99.79056653	99.79387454
βv	1.410083658	92.75462306	106.8261737
βH	0.4159130384	97.60788141	101.768767

Berdasarkan Tabel 5, bahwa tingkat gigitan nyamuk rentan dan terinfeksi b memiliki pengaruh paling positif dengan jumlah nyamuk yang terinfeksi I_v, artinya semakin tinggi tingkat gigitan nyamuk rentan dan terinfeksi b, maka semakin tinggi juga nyamuk yang terinfeksi (I_v). Laju kematian nyamuk μ_v memiliki hubungan paling negatif dengan jumlah nyamuk yang terinfeksi I_v, artinya semakin tinggi laju kematian nyamuk μ_v, berdampak pada jumlah nyamuk yang terinfeksi (I_v) semakin rendah.

• 3.4 Simulasi Numerik

Pada subbab ini dijelaskan simulasi numerik menggunakan beberapa nilai parameter yang berhubungan dengan Analisis Sensitivitas.

• 3.4.1    Efek perubahan nilai laju kematian manusia (μ∣∣)

Perubahan nilai parameter (μ∏) mengakibatkan jumlah manusia yang terinfeksi (I_h) mengalami perubahan. Berdasarkan Gambar 2 (b), bertambahnya nilai μ_H sebesar 5%, mengakibatkan bertambahnya jumlah I_h 4,99%. Sebaliknya apabila nilai μ_H turun sebesar 5%, maka jumlah manusia yang terifeksi demam berdarah dengue juga mengalami penurunan sebesar 4,99%.

(a)                                                    (b)

Gambar 2. (a) Efek μ_H terhadap I_h, (b) plot I_h terhadap waktu dengan beberapa nilai parameter ^h

• 3.4.2    Efek perubahan nilai laju kematian nyamuk (μ_v)

Hubungan negatif antara (μ_v) dengan bilangan reproduksi dasar (Rq) terlihat pada Gambar 3 (a). Semakin naik nilai (μ_v), maka (R_q) menurun. Berdasarkan Gambar 3 (b), meningkatnya nilai laju kematian nyamuk sebesar 5%, mengakibatkan menurunnya R_q sebesar 10.86%. Artinya, meningkatnya laju kematian nyamuk akan menyebabkan menurunnya infeksi sekunder, sehingga hal ini menekan penyebaran penyakit demam berdarah dengue.

Laju kematian nyamuk (μ_v) juga memiliki hubungan negatif dengan jumlah manusia yang terinfeksi demam berdarah dengue (I_h) seperti pada Gambar 4 (a). Berdasarkan Gambar 4 (b), jika laju kematian nyamuk meningkat sebesar 5%, maka jumlah manusia yang terinfeksi demam berdarah dengue menurun 5,94%. Artinya bahwa meningkatnya laju kematian nyamuk dapat menekan penyebaran penyakit demam berdarah dengue.

(a)

(b)

Gambar 3. (a) Efek μ_v terhadap R₀, (b) plot R₀ terhadap Waktu dengan beberapa nilai parameter

Rv

(a)

(b)

Gambar 4. (a) Efek μ_v terhadap I_h, (b) plot I_h terhadap Waktu dengan beberapa nilai parameter

^μv

Berdasarkan Gambar 5 (a), laju kematian nyamuk (μ_v) memiliki hubungan negatif dengan jumlah nyamuk yang terinfeksi demam berdarah dengue (I_v). Gambar 5 (b) menunjukkan Jika laju kematian nyamuk meningkat sebesar 5%, maka jumlah nyamuk yang terinfeksi demam berdarah dengue menurun 15,35%, bahwa meningkatnya laju kematian nyamuk dapat menekan penyebaran penyakit demam berdarah dengue.

(a)                                                    (b)

Gambar 5. (a) Efek μ_v terhadap l_v, (b) plot I_v terhadap Waktu dengan beberapa nilai parameter l^lv

• 3.4.3    Efek perubahan tingkat gigitan nyamuk (b)

Gambar 6 (a) menunjukkan bahwa tingkat gigitan nyamuk (b') berpengaruh positif terhadap bilangan reproduksi dasar (R₀). Berdasarkan Gambar 6 (b), meningkatnya tingkat gigitan nyamuk sebesar 5% mengakibatkan meningkatnya infeksi sekunder sebesar 5% juga. Penyebaran penyakit demam berdarah dengue akan meningkat apabila tingkat gigitan nyamuk juga meningkat.

(a)                                                    (b)

Gambar 6. (a) Efek b terhadap R₀, (b) plot R₀ terhadap Waktu dengan beberapa nilai parameter b

Tingkat gigitan nyamuk juga berpengaruh positif terhadap nyamuk yang terinfeksi virus demam berdarah dengue. Gambar 7 (b) menunjukkan bahwa kenaikan 5% tingkat gigitan nyamuk secara tidak langsung mengakibatkan meningkatnya nyamuk yang terinfeksi virus dengue sebesar 9%. Hal ini menandakan bahwa dalam Sistem (1), jika

tingkat gigitan nyamuk naik, maka akan meningkatnya nyamuk yang terinfeksi sehingga peluang penyebaran penyebaran penyakit demam berdarah dengue juga meningkat.

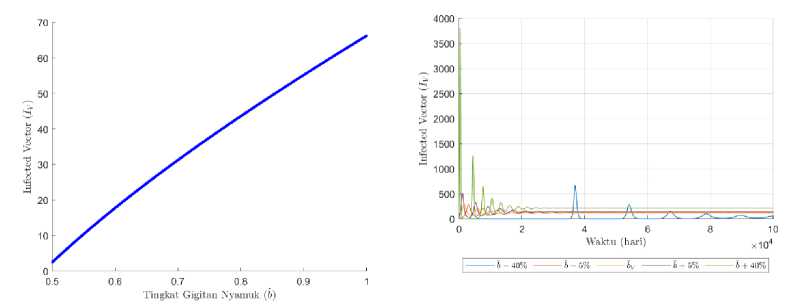
(a)                                                    (b)

Gambar 7. (a) Efek b terhadap I_v, (b) plot I_v terhadap Waktu dengan beberapa nilai parameter b

• 3.4.4    Efek perubahan laju kesembuhan manusia (r)

Laju kesembuhan manusia memiliki hubungan negatif dengan manusia yang terinfeksi (I_h) seperti yang ditunjukkan Gambar 8 (a). Selanjutnya, Berdasarkan Gambar 8 (b), meningkatnya laju kesembuhan manusia sebesar 5% mengakibatkan menurunnya jumlah manusia yang terinfeksi sebesar 3,9%. Dalam Sistem (1) semakin banyak individu yang sembuh, maka semakin menurunnya jumlah individu yang terinfeksi virus dengue, hal ini diperkuat oleh asumsi pada penelitian ini bahwa individu yang sudah terinfeksi oleh serotipe virus tertentu, tidak akan terinfeksi oleh serotipe virus lainnya.

(a)

(b)

Gambar 8. Efek r terhadap I_h , (b) plot I_h terhadap Waktu dengan beberapa nilai parameter r

4. Kesimpulan dan Saran

Analisis sensitivitas pada model Matematika Penyebaran Penyakit Demam Dengue dengan Laju Insidensi NonLinier dilakukan untuk melihat parameter yang memiliki pengaruh paling dominan. Diperoleh bahwa tingkat gigitan nyamuk rentan dan terinfeksi (S) memiliki hubungan yang positif , sedangkan laju kematian nyamuk memiliki hubungan yang negatif terhadap R₀. Kenaikan nilai parameter (S) mengakibatkan nilai R₀ juga mengalami kenaikan, sedangkan kenaikan nilai parameter μ_v mengakibatkan nilai R₀ turun, berlaku juga sebaliknya. Selanjutnya laju kesembuhan manusia (r) memiliki hubungan yang negatif dengan I_h , artinya kenaikan laju kesembuhan manusia (r), berdampak pada menurunnya jumlah manusia yang terinfeksi (I_h). Hubungan negatif terjadi pada μ_v dengan I_h artinya, semakin naik nilai μ_v, maka nilai I_h semakin turun. Selanjutnya, μ_ll memiliki hubungan yang positif dengan I_h , artinya semakin naik μ_ll, maka nilai I_h semakin turun. Tingkat gigitan nyamuk rentan dan terinfeksi b memiliki pengaruh paling positif dengan jumlah nyamuk yang terinfeksi I_v, artinya semakin tinggi tingkat gigitan nyamuk rentan dan terinfeksi b, maka semakin tinggi juga nyamuk yang terinfeksi (I_v). Laju kematian nyamuk μ_v memiliki hubungan paling negatif dengan jumlah nyamuk yang terinfeksi I_v, artinya semakin tinggi laju kematian nyamuk μ_v, berdampak pada jumlah nyamuk yang terinfeksi (I_v) semakin rendah.

Saran untuk penelitian selanjutnya dapat dilakukan analisis sensitivitas dengan metode Partial Rank Correlation Coefficients (PRCC) atau metode Monte-Carlo (MC).

Daftar Pustaka

Bhatt, P., Sabeena, S. P., Varma, M., & Arunkumar, G. (2021). Current Understanding of the Pathogenesis of Dengue Virus Infection. Current Microbiology, 78(1), 17–32. https://doi.org/10.1007/s00284-020-02284-w

Biswas, P., Ganguly, S., & Debnath, B. (2021). Dengue fever: Stages, complication, diagnosis, and prevention strategies. Asian J Pharm Clin Res, 14(5), 3–11.

Chitnis, N., Hyman, J. M., & Cushing, J. M. (2008). Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model. Bulletin      of      Mathematical      Biology,      70(5),      1272–1296.

https://doi.org/10.1007/s11538-008-9299-0

Eivazzadeh-Keihan, R., Pashazadeh-Panahi, P., Mahmoudi, T., Chenab, K. K., Baradaran, B., Hashemzaei, M., Radinekiyan, F., Mokhtarzadeh, A., & Maleki, A. (2019). Dengue virus: a review on advances in detection and trends – from conventional

methods to novel biosensors. Microchimica   Acta,   186(6),   329.

https://doi.org/10.1007/s00604-019-3420-y

Guo, C., Zhou, Z., Wen, Z., Liu, Y., Zeng, C., Xiao, D., Ou, M., Han, Y., Huang, S., & Liu, D. (2017). Global epidemiology of dengue outbreaks in 1990–2015: a systematic review and meta-analysis. Frontiers in cellular and infection microbiology, 7, 317.

Halstead, S., & Wilder-Smith, A. (2019). Severe dengue in travellers: pathogenesis, risk and clinical management. Journal of Travel Medicine,  26(7),  taz062.

https://doi.org/10.1093/jtm/taz062

Jing, Q., & Wang, M. (2019). Dengue epidemiology. Global Health Journal, 3(2), 37–45. https://doi.org/https://doi.org/10.1016/j.glohj.2019.06.002

Messina, J. P., Brady, O. J., Golding, N., Kraemer, M. U. G., Wint, G. R. W., Ray, S. E., Pigott, D. M., Shearer, F. M., Johnson, K., Earl, L., Marczak, L. B., Shirude, S., Davis Weaver, N., Gilbert, M., Velayudhan, R., Jones, P., Jaenisch, T., Scott, T. W., Reiner, R. C., & Hay, S. I. (2019). The current and future global distribution and population at risk of dengue. Nature  Microbiology,  4(9),  1508–1515.

https://doi.org/10.1038/s41564-019-0476-8

Mukherjee, D., Das, S., Begum, F., Mal, S., & Ray, U. (2019). The Mosquito Immune System and the Life of Dengue Virus: What We Know and Do Not Know. Pathogens, 8(2). https://doi.org/10.3390/pathogens8020077

Mutheneni, S. R., Morse, A. P., Caminade, C., & Upadhyayula, S. M. (2017). Dengue burden in India: recent trends and importance of climatic parameters. Emerg Microbes Infect, 6(8), e70. https://doi.org/10.1038/emi.2017.57

Mwanyika, G. O., Mboera, L. E. G., Rugarabamu, S., Ngingo, B., Sindato, C., Lutwama, J. J., Paweska, J. T., & Misinzo, G. (2021). Dengue Virus Infection and Associated Risk Factors in Africa: A Systematic Review and Meta-Analysis. Viruses, 13(4). https://doi.org/10.3390/v13040536

Nanaware, N., Banerjee, A., Mullick Bagchi, S., Bagchi, P., & Mukherjee, A. (2021). Dengue Virus Infection: A Tale of Viral Exploitations and Host Responses. Viruses, 13(10). https://doi.org/10.3390/v13101967

Pathak, V. K., & Mohan, M. (2019). A notorious vector-borne disease: Dengue fever, its evolution as public health threat. J Family Med Prim Care, 8(10), 3125–3129. https://doi.org/10.4103/jfmpc.jfmpc_716_19

Pereira, T. N., Carvalho, F. D., De Mendonça, S. F., Rocha, M. N., & Moreira, L. A. (2020). Vector competence of Aedes aegypti, Aedes albopictus, and Culex quinquefasciatus mosquitoes for Mayaro virus. PLOS Neglected Tropical Diseases, 14(4), e0007518.

Pongsumpun, P. (2008). Mathematical model of dengue disease with the incubation period of virus. World Academy of Science, Engineering and Technology, 44, 328–332.

Rosmalena, R., Elya, B., Dewi, B. E., Fithriyah, F., Desti, H., Angelina, M., Hanafi, M., Lotulung, P. D., Prasasty, V. D., & Seto, D. (2019). The Antiviral Effect of Indonesian Medicinal Plant Extracts Against Dengue Virus In Vitro and In Silico. Pathogens, 8(2). https://doi.org/10.3390/pathogens8020085

Saxena, S. K., Kumar, S., Maurya, V. K., & Bhatt, M. L. B. (2019). The Global Distribution and Burden of Dengue and Japanese Encephalitis Co-Infection in Acute Encephalitis Syndrome. Dalam A. J. Rodriguez-Morales (Ed.), Current Topics in

Neglected     Tropical     Diseases     (hlm.     Ch.     2).     IntechOpen.

https://doi.org/10.5772/intechopen.89792

Van den Driessche, P., & Watmough, J. (2002). Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical biosciences, 180(1–2), 29–48.

WHO. (2012). dengue hemorrhagic fever, fact sheet 117, revised January 2022. Geneva:

World Health Organization. http://www.who.int/mediacentre/factsheets/fs117/en/

Wilder-Smith, A., Ooi, E.-E., Horstick, O., & Wills, B. (2019). Dengue. The Lancet, 393(10169), 350–363.

143