Rancangan dan Analisis Model Algoritma Genetika Untuk Menyelesaikan Permasalahan Knapsack 2 Dimensi

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 11, No 2. November 2022

Rancangan dan Analisis Model Algoritma Genetika Untuk Menyelesaikan Permasalahan Knapsack 2 Dimensi

Devan Bramantya^a1, I Gede Santi Astawa^a2, I Wayan Supriana^a3, Luh Gede Astuti^a4, Ngurah Agus Sanjaya ER^a5, I Gusti Agung Gede Arya Kadyanan^a6

^aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana Badung, Bali, Indonesia

¹[email protected] ²[email protected] ³[email protected] ⁴[email protected] ⁵[email protected] ⁶[email protected]

Abstract

The knapsack problem is problem that is still often found in everyday life, one of which is the problem of selecting goods to be transported into containers for delivery of goods. This knapsack problem can be solved by using various optimization algorithms, one of which is the genetic algorithm. This study aims to design a genetic algorithm model to solve the 2-dimensional knapsack problem. 2dimensional knapsack problem is a knapsack problem that has 2 constraints and in this study, the constraints used were weight and volume. The evaluation results of the genetic algorithm will be compared with dynamic programming. From the evaluation results that have been carried out, it can be concluded that genetic algorithms can produce near-optimal results with faster computational times than dynamic programming.

Keywords: 2-Dimensional Knapsack Problem, Optimization, Shipping Goods, Genetic Algorithm, Dynamic Programming

• 1.    Pendahuluan

Kontainer atau peti kemas merupakan sebuah kotak besar yang digunakan untuk mengangkut barang yang diangkut menggunakan kapal angkut, truk atau kereta api sampai ke tempat tujuan. Menurut Kepala Badan Pusat Statistik (BPS), Suhariyanto menyampaikan bahwa jumlah barang yang diangkut kereta api pada bulan januari-maret 2020 mengalami peningkatan sebesar 5,10% menjadi 74,6 juta ton dibandingkan dengan periode yang sama pada tahun 2019. Dengan meningkatnya pengangkutan barang tersebut, terdapat kendala yang dihadapi oleh perusahaan peti kemas, yaitu kurangnya kontrol dalam melakukan muat barang yang menyebabkan penggunaan peti kemas tidak optimal. Permasalahan dimana orang dihadapkan pada pemilihan benda yang dapat dimasukkan ke dalam sebuah wadah yang memiliki keterbatasan ruang atau daya tampung disebut dengan Knapsack problem [1]. Salah satu jenis dari permasalahan Knapsack adalah Multidimensional Knapsack Problem dimana terdapat beberapa barang yang harus dipilih dengan kendala atau constraint lebih dari satu [2]. Kendala atau constraint yang ada pada kasus kontainer ini adalah kendala volume dan berat barang dimana barang-barang yang akan dimasukkan ke dalam kontainer tidak boleh melebihi kapasitas volume ataupun berat yang bisa ditampung oleh kontainer. Permasalahan Knapsack ini dapat diselesaikan dengan menggunakan berbagai algoritma salah satunya adalah algoritma genetika. Algoritma genetika merupakan algoritma yang menggunakan evolusi alam sebagai gagasan utamanya dalam menyelesaikan suatu permasalahan tertentu [3]. Algoritma genetika dimulai dengan membangkitkan sejumlah populasi individu awal. Populasi tersebut akan melalui beberapa proses mulai dari Crossover atau persilangan, Mutasi, Perhitungan Nilai Fitness dan Seleksi untuk mendapatkan populasi yang baru. Proses-proses tersebut akan terus diulang hingga mencapai batas generasi yang telah ditentukan atau hasil yang optimal sudah didapatkan.

Penelitian mengenai optimasi penyelesaian knapsack problem sudah pernah dilakukan oleh beberapa peneliti lainnya seperti penelitian yang membahas mengenai bagaimana menyelesaikan masalah knapsack multidimensi dengan menggunakan algoritma greedy yang menghasilkan solusi yang memiliki rata-rata selisih 20% dari solusi optimal [4]. Kemudian penelitian yang membahas

Bramantya, dkk.

Rancangan dan Analisis Model Algoritma Genetika Untuk Menyelesaikan Permasalahan Knapsack 2 Dimensi mengenai permasalahan optimasi untuk mengangkut barang berupa pupuk dan kebutuhan pertanian dengan mempertimbangkan berat dan keuntungan dari barang yang diangkut agar dapat memperoleh keuntungan maksimal. Penelitian tersebut mengungkap bahwa penggunaan algoritma dynamic programming cukup baik digunakan karena berhasil memenuhi 99,683% dari kapasitas truk [ 5]. Penelitian selanjutnya adalah penelitian yang menggunakan algoritma genetika untuk menyelesaikan permasalahan knapsack dengan nilai error 0% pada ukuran populasi tertentu pada masing-masing test problem dan nilai parameter Crossover rate sebesar 0.2 dan Mutation rate sebesar 0.8 dengan iterasi 100 generasi [6].

Berdasarkan penelitian yang sudah dilakukan tersebut, penggunaan algoritma greedy untuk menyelesaikan permasalahan knapsack multidimensi masih kurang baik, sehingga pada penelitian ini akan dilakukan pengimplementasian model algoritma genetika untuk mengoptimalkan penyelesaian 2-Dimensional Knapsack Problem dengan menggunakan menggunakan Variable-Length Chromosome, dimana setiap kromosom dapat memiliki jumlah gen yang berbeda-beda bergantung dari banyaknya barang yang terpilih pada kromosom tersebut. Hasil dari algoritma genetika tersebut akan dibandingkan dengan hasil dari Dynamic Programming.

• 2.    Metode Penelitian

Penelitian ini dilakukan dengan beberapa tahapan yaitu, dimulai dari pengumpulan data, pengimplementasian algoritma genetika dan dynamic programming menggunakan bahasa pemrograman Java dan tahap pengujian.

• 2.1.    Pengumpulan Data

Data yang digunakan pada penelitian ini adalah data dummy dimana data-data tersebut merupakan data-data barang yang akan dikirim menggunakan kontainer. Data-data tersebut dibuat sedemikian rupa sehingga mendekati data asli dimana jasa pengiriman barang menerima permintaan pengiriman barang dari orang-orang untuk dikirimkan menggunakan kontainer. Terdapat 90 data barang yang akan digunakan dalam penelitian ini. Data barang tersebut dilengkapi dengan data berat barang dalam satuan kilogram dan volume barang dalam satuan centimeter.

• 2.2.    Algoritma Genetika

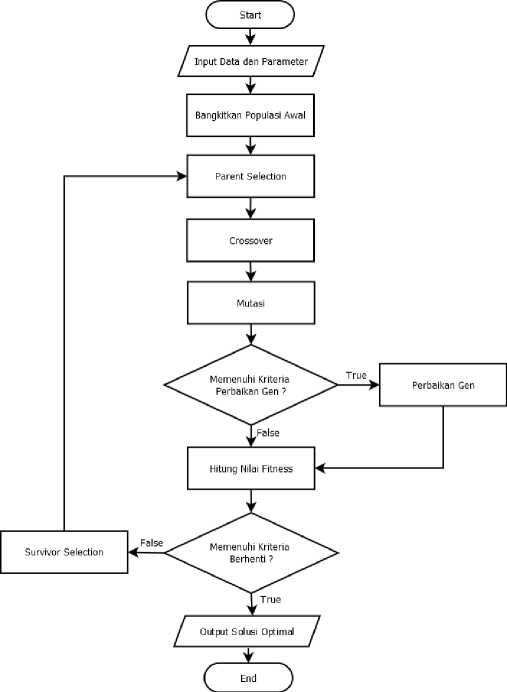
Gambar 1. Flowchart Algoritma Genetika

Gambar 1 menunjukkan flowchart dari algoritma genetika. Flowchart tersebut dimulai dari user yang akan diminta untuk menginputkan data-data barang dan parameter-parameter yang akan digunakan dalam proses algoritma genetika seperti crossover rate, mutation rate, jumlah maksimum generasi dan jumlah populasi. Kemudian sistem akan membangkitkan sejumlah kromosom sebagai populasi awal secara acak sesuai dengan jumlah individu yang sudah diinputkan. Selanjutnya proses Parent Selection dilakukan untuk memilih kromosom-kromosom yang akan digunakan untuk proses crossover. Metode yang akan digunakan dalam Seleksi parent adalah metode Roulette Wheel. Jumlah parent yang dipilih akan bergantung pada nilai dari parameter crossover rate. Kemudian akan dilakukan proses crossover dengan menggunakan kromosom-kromosom yang terpilih pada proses sebelumnya dengan metode Uniform Crossover. Proses selanjutnya adalah proses mutasi dengan memilih sejumlah kromosom secara acak dan mengubah gen-gen tertentu dalam kromosom tersebut. Jumlah kromosom yang dipilih akan bergantung pada nilai dari parameter mutation rate. Jika total volume atau berat barang melebihi kapasitas maksimal, maka akan dilakukan perbaikan gen dengan mengganti gen yang memiliki volume barang atau berat barang terbesar dengan barang lain yang memiliki volume atau berat barang yang lebih kecil secara acak. Selanjutnya adalah pehitungan nilai fitness dengan rumus sebagai berikut :

(    ⅛-)

(1)

Fitness =

2

Keterangan :

i   = barang ke-i

n = jumlah barang

v = volume barang

b = berat barang

• V = kapasitas volume maksimum yang dapat ditampung oleh knapsack

B = kapasitas berat maksimum yang dapat ditampung oleh knapsack

Jika populasi tersebut sudah menemukan hasil yang optimal atau ketika generasi sudah mencapai batas generasi maksimum yang sudah ditetapkan sebelumnya, maka proses algoritma genetika akan dihentikan dan hasil optimal tersebut akan ditampilkan. Jika belum, maka akan dilakukan proses Survivor Selection. Proses Survivor Selection dilakukan untuk memilih kromosom-kromosom yang akan dipertahankan di generasi selanjutnya. Kromosom akan dipilih berdasarkan nilai fitness terbaik dan jumlah kromosom yang dipilih bergantung pada jumlah populasi awal.

• 2.3.    Dynamic Programming

  

  Gambar 2. Flowchart Dynamic Programming

  
  

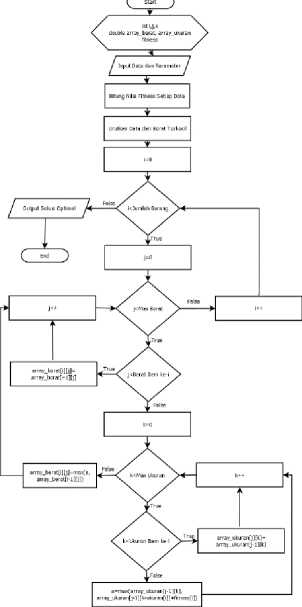
Gambar 2 menunjukkan flowchart dari dynamic programming. Flowchart tersebut dimulai dengan menginisialisasi variabel-variabel yang akan digunakan, kemudian user akan diminta untuk menginputkan data-data barang dan parameter-parameter yang akan digunakan dalam proses dynamic programming yaitu maksimum berat dan maksimum volume. Setiap data barang yang diinputkan akan dihitung nilai fitnessnya dengan rumus :

Fitness = (^

(2)

2

Keterangan : i   = barang ke-i

v = volume barang

b = berat barang

• V = kapasitas volume maksimum yang dapat ditampung oleh knapsack

B = kapasitas berat maksimum yang dapat ditampung oleh knapsack

Tahap selanjutnya adalah mengurutkan data barang dari yang paling ringan hingga paling berat. Kemudian akan dilakukan perulangan variabel i dari 0 sampai dengan jumlah barang. Selanjutnya lakukan perulangan variabel j dari 0 sampai dengan maksimum berat. Selama perulangan j tersebut, jika variabel j lebih kecil dari berat barang ke-i, maka nilai dari array_berat[i][j] = array_berat[i-1][j]. Jika tidak, maka lakukan perulangan variabel k dari 0 hingga sampai dengan maksimum volume. Selama perulangan k tersebut, jika variabel k lebih kecil dari volume barang ke-i, maka nilai dari array_ukuran[j][k] = array_ukuran[j-1][k]. Jika tidak, maka cari nilai yang lebih besar di antara array_ukuran[j-1][k] dan array_ukuran[j-1][k-ukuran[i]]+fitness[i] dan simpan nilai tersebut pada variabel a. Setelah perulangan k tersebut selesai, cari nilai yang lebih besar diantara a dan array_berat[i-1][j] dan simpan hasilnya pada array_berat[i][j]. Setelah perulangan j tersebut selesai, maka nilai i akan bertambah 1 dan lakukan kembali langkah f hingga j. Jika nilai i sudah melebihi jumlah barang, maka program akan menampilkan solusi optimal.

• 2.4.    Pengujian

Pengujian pertama yang dilakukan adalah sebagai berikut :

• a.    Mencari nilai crossover rate terbaik dengan cara mengubah-ubah nilai crossover rate dan melihat hasil dari setiap nilai crossover rate yang digunakan.

• b.    Mencari nilai mutation rate terbaik dengan cara mengubah-ubah nilai mutation rate dan melihat hasil dari setiap nilai mutation rate yang digunakan.

• c.    Mencari nilai Maksimum Generasi terbaik dengan cara mengubah-ubah nilai Maksimum Generasi dan melihat hasil dari setiap nilai Maksimum Generasi yang digunakan.

• d.    Mencari nilai Jumlah Populasi terbaik dengan cara mengubah-ubah nilai Jumlah Populasi dan melihat hasil dari setiap nilai Jumlah Populasi yang digunakan.

Dari hasil pengujian tersebut, maka akan dilakukan penyimpulan dengan cara melihat nilai crossover rate terbaik, mutation rate terbaik, maksimum generasi dan jumlah populasi awal terbaik.

Pengujian kedua yang dilakukan adalah sebagai berikut :

• a.    Membandingkan hasil optimasi dari algoritma genetika dan dynamic programming.

• b.    Membandingkan waktu komputasi dari algoritma genetika dan dynamic programming.

Dari hasil pengujian tersebut, akan didapat kesimpulan mengenai kinerja dari algoritma genetika dan dynamic programming dalam permasalahan knapsack 2 dimensi.

• 3.    Hasil dan Pembahasan

Pada penelitian ini, penulis melakukan pengujian untuk mengetahui berapa nilai parameter algoritma genetika terbaik yang dapat menghasilkan hasil yang optimal atau mendekati optimal dan mengetahui bagaimana kinerja algoritma genetika jika dibandingkan dengan dynamic programming dalam penyelesaian knapsack problem dua dimensi.

• 3.1.    Implementasi Sistem

Proses pengimplementasian algoritma genetika dan Dynamic Programming dilakukan dengan menggunakan bahasa pemrograman Java dengan menggunakan aplikasi NetBeans. Tampilan dari aplikasi desktop yang telah dibuat dapat dilihat pada gambar 3.

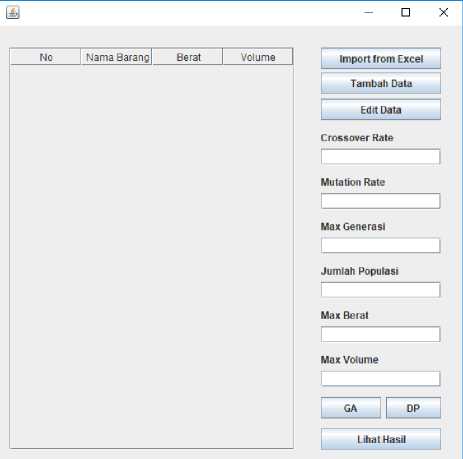
Gambar 3. Tampilan Interface aplikasi

Pada gambar 3 dapat dilihat tampilan halaman utama dari aplikasi yang sudah dibuat. Terdapat beberapa tombol pada halaman utama aplikasi tersebut yang dapat dilihat pada gambar 3 diatas. Diantaranya adalah Import From Excel, Tambah Data, Edit Data, GA, DP dan Lihat Hasil. Tombol Import From Excel dapat digunakan untuk menginputkan data secara otomatis dari file excel yang ada. Tombol Tambah Data dapat digunakan untuk menambahkan data secara manual. Ketika tombol ini ditekan, maka user akan diminta untuk memasukkan nama, berat dan volume barang, setelah itu klik tombol Add untuk menambahkan barang. Tombol selanjutnya adalah Edit Data. Tombol ini digunakan untuk mengubah data yang sudah diinputkan. User harus memilih salah satu data yang ada pada tabel terlebih dahulu sebelum menekan tombol Edit Data tersebut. Tombol selanjutnya adalah tombol GA dan DP. Tombol GA digunakan untuk memproses data tersebut dengan menggunakan Algoritma Genetika sedangkan DP digunakan untuk memproses data tersebut dengan Dynamic Programming. Sebelum menekan salah satu dari kedua tombol tersebut, user diharuskan untuk mengisi form yang tersedia terlebih dahulu seperti Crossover Rate, Mutation Rate, Max Generasi, Jumlah Populasi, Max Berat dan Max Volume. Setelah salah satu dari kedua tombol tersebut ditekan, maka anda harus menunggu hingga proses selesai dan jika sudah selesai, user harus menekan tombol Lihat Hasil untuk melihat hasil pemrosesan algoritma genetika atau dynamic programming tersebut.

• 3.2.    Pengujian Parameter Algoritma Genetika

Pengujian akan dilakukan dengan menggunakan parameter Maksimum Generasi sebesar 50 dan 100, Jumlah Populasi sebesar 50, 75 dan 100, Crossover Rate sebesar 0.5, 0.6, dan 0.7, Mutation Rate sebesar 0.1 dan 0.2. Pemilihan parameter tersebut didasari oleh penelitian yang dilakukan oleh DeJong [7] yang mengatakan bahwa nilai optimal untuk jumlah populasi adalah sebesar 50 hingga 100, mutation rate sebesar 0.1 dan crossover rate sebesar 0.6. Grefenstette [8] juga mengatakan bahwa crossover rate yang tinggi akan berjalan selaras dengan mutation rate yang rendah. Maksimum Berat dan Maksimum Volume yang akan digunakan merupakan ukuran asli kontainer 20ft yaitu 5,758m x 2,352m x 2,385m yang jika diubah kedalam centimeter dan dihitung volumenya, maka akan menjadi sekitar 32.000.000cm dan memiliki kapasitas maksimum berat sebesar 21.800 kg. Pengujian juga akan dilakukan dengan menggunakan Maksimum Berat dan Maksimum Volume dari kontainer mobil box dengan ukuran 230cm x 160cm x 125cm yang jika dihitung volumenya adalah 4.600.000cm dengan kapasitas maksimum berat sebesar 800kg. Hasil pengujian pada kontainer 20ft dapat dilihat pada Gambar 4 hingga Gambar 6 dan pengujian pada kontainer mobil box dapat dilihat pada Gambar 7 hingga Gambar 9.

Gambar 4 menunjukkan hasil pengujian pada Kontainer 20ft dengan jumlah populasi 50, crossover rate 0.5, 0.6, 0.7, mutation rate 0.1, 0.2, maksimum generasi 25 dan 50. Dari pengujian tersebut, didapatkan hasil nilai fitness tertinggi sebesar 0.5376 dengan terpilihnya 42 dari 90 barang pada pengujian dengan jumlah populasi 50, crossover rate 0.6, mutation rate 0.2, maksimum generasi 50.

	Jumlah Populasi 50
0.55 ω ⊂  0.5 0.45 03 0.4 Z	0.53562585                 00...55335175561                 00..5523245621707958 0.47864           0.49898 0.5                   0.6                   0.7 Crossover Rate

-^MR=0.1, Max Generasi=25^^—MR=0.2, Max Generasi=25

^^—MR=0.1, Max Generasi=50^^—MR=0.2, Max Generasi=50

Gambar 4. Hasil pengujian pada Kontainer 20ft dengan Jumlah Populasi 50

Gambar 5 menunjukkan hasil pengujian pada Kontainer 20ft dengan jumlah populasi 75, crossover rate 0.5, 0.6, 0.7, mutation rate 0.1, 0.2, maksimum generasi 25 dan 50. Dari pengujian tersebut, didapatkan hasil nilai fitness tertinggi sebesar 0.53879 dengan terpilihnya 45 dari 90 barang pada pengujian dengan jumlah populasi 75, crossover rate 0.7, mutation rate 0.1, maksimum generasi 50.

Jumlah Populasi 75

in 0.56 ω 0.54 S 0.52 0.5 ≡ 0.48 ≥ 0.46

0.53563794                 0..5368146                 0..5386799 0.51559           0.51404            . 0.5                  0.6                  0.7

Crossover Rate

^^—MR=0.1, Max Generasi=25^^— MR=0.2, Max Generasi=25

^^—MR=0.1, Max Generasi=50^^— MR=0.2, Max Generasi=50

Gambar 5. Hasil pengujian pada Kontainer 20ft dengan Jumlah Populasi 75

Gambar 6 menunjukkan hasil pengujian pada Kontainer 20ft dengan jumlah populasi 100, crossover rate 0.5, 0.6, 0.7, mutation rate 0.1, 0.2, maksimum generasi 25 dan 50. Dari pengujian tersebut, didapatkan hasil nilai fitness tertinggi sebesar 0.53736 dengan terpilihnya 41 dari 90 barang pada pengujian dengan jumlah populasi 100, crossover rate 0.7, mutation rate 0.2, maksimum generasi 50.

Jumlah Populasi 100

0.5                0.6                0.7

Crossover Rate

0.05.3536676

0.54

0.52

0.5

ΓD

0.48

0.52433

0.5

^^—MR=0.1, Max Generasi=25     MR=0.2, Max Generasi=25

•  MR=0.1, Max Generasi=50—^ MR=0.2, Max Generasi=50

Gambar 6. Hasil pengujian pada Kontainer 20ft dengan Jumlah Populasi 100

Gambar 7 menunjukkan hasil pengujian pada Mobil Box dengan jumlah populasi 50, crossover rate 0.5, 0.6, 0.7, mutation rate 0.1, 0.2, maksimum generasi 25 dan 50. Dari pengujian tersebut,

didapatkan hasil nilai fitness tertinggi sebesar 0.81042 dengan terpilihnya 24 dari 90 barang pada pengujian dengan jumlah populasi 50, crossover rate 0.5, mutation rate 0.2, maksimum generasi 50.

Jumlah Populasi 50

0.85

0.81042 0⁰.^.7⁷7⁸8⁹3²7⁷

0.7

0.5                  0.6                 0.7

0.8

0.75

⅛  0.7

Crossover Rate

-^MR=0.1, Max Generasi=25^^— MR=0.2, Max Generasi=25

^^—MR=0.1, Max Generasi=50^^— MR=0.2, Max Generasi=50

Gambar 7. Hasil pengujian pada Mobil Box dengan Jumlah Populasi 50

Gambar 8 menunjukkan hasil pengujian pada Mobil Box dengan jumlah populasi 75, crossover rate 0.5, 0.6, 0.7, mutation rate 0.1, 0.2, maksimum generasi 25 dan 50. Dari pengujian tersebut, didapatkan hasil nilai fitness tertinggi sebesar 0.81729 dengan terpilihnya 24 dari 90 barang pada pengujian dengan jumlah populasi 75, crossover rate 0.7, mutation rate 0.2, maksimum generasi 50.

Jumlah Populasi 75

$ 0.85           ₀0_0.._.78₇₈0₉₅0₃₀7₃₆6               ₀₀0_...₇₇8₇₈₉1₂₃₂4₈₁₃9₃₇₈3               ₀00_{0 7}78₇₇91₉₈67₃₄62₉₆49

OJ  0.8       0.75396          ^{0.77283            .}

0.75

rσ 0.7

z              0.5              0.6              0.7

Crossover Rate

—^-MR=0.1, Max Generasi=25^^— MR=0.2, Max Generasi=25

^^—MR=0.1, Max Generasi=50^^— MR=0.2, Max Generasi=50

Gambar 8. Hasil pengujian pada Mobil Box dengan Jumlah Populasi 75

Gambar 9 menunjukkan hasil pengujian pada Mobil Box dengan jumlah populasi 100, crossover rate 0.5, 0.6, 0.7, mutation rate 0.1, 0.2, maksimum generasi 25 dan 50. Dari pengujian tersebut, didapatkan hasil nilai fitness tertinggi sebesar 0.82552 dengan terpilihnya 25 dari 90 barang pada pengujian dengan jumlah populasi 100, crossover rate 0.5, mutation rate 0.2, maksimum generasi 50.

Jumlah Populasi 100

0.85 ∞ OJ ⊂  0.8 jp 0.75 2  0.7

0.82552         0.81688         0.81801 0..7631            0.77444           0..77151 0.5                0.6                0.7

Crossover Rate

—^-MR=0.1, Max Generasi=25  •  MR=0.2, Max Generasi=25

•  MR=0.1, Max Generasi=50  •  MR=0.2, Max Generasi=50

Gambar 9. Hasil pengujian pada Mobil Box dengan Jumlah Populasi 100

Dari hasil pengujian pada gambar 4 hingga 9, dapat dilihat bahwa Algoritma Genetika dapat menghasilkan Nilai Fitness paling besar sebanyak 0.53879 untuk pengujian pada kontainer 20ft (Jumlah Populasi=100, Maksimum Generasi=50, Crossover Rate=0.5 dan Mutation Rate=0.2) dan 0.82552 untuk pengujian pada mobil box (Jumlah Populasi=100, Maksimum Generasi=50, Crossover Rate=0.5 dan Mutation Rate=0.2). Untuk mengetahui berapa nilai parameter terbaik, maka akan dilakukan perhitungan rata-rata dari nilai fitness untuk setiap parameter yang digunakan. Hasil perhitungan tersebut dapat dilihat pada tabel 1 hingga 4.

Tabel 1. Rata-rata Nilai Fitness untuk Crossover Rate

Crossover Rate	Rata-Rata Nilai Fitness pada Kontainer 20ft	Rata-Rata Nilai Fitness pada Mobil Box
0.5	0.520913333	0.78574
0.6	0.526835	0.790430833
0.7	0.531505	0.7932025

Tabel 1 menunjukkan rata-rata nilai fitness untuk Crossover Rate yang didapatkan dari pengujian pada Kontainer 20ft dan Mobil Box. Rata-rata nilai fitness tertinggi didapatkan dari penggunaan parameter crossover rate sebesar 0.7.

Tabel 2. Rata-rata Nilai Fitness untuk Mutation Rate

Mutation Rate	Rata-Rata Nilai Fitness pada Kontainer 20ft	Rata-Rata Nilai Fitness pada Mobil Box
0.1	0.521722778	0.779824444
0.2	0.531112778	0.799757778

Tabel 2 menunjukkan rata-rata nilai fitness untuk Mutation Rate yang didapatkan dari pengujian pada Kontainer 20ft dan Mobil Box. Rata-rata nilai fitness tertinggi didapatkan dari penggunaan parameter Mutation Rate sebesar 0.2.

Tabel 3. Rata-rata Nilai Fitness untuk Maksimum Generasi

Maksimum Generasi	Rata-Rata Nilai Fitness pada Kontainer 20ft	Rata-Rata Nilai Fitness pada Mobil Box
25	0.516240556	0.777567222
50	0.536595	0.802015

Tabel 3 menunjukkan rata-rata nilai fitness untuk maksimum generasi yang didapatkan dari pengujian pada Kontainer 20ft dan Mobil Box. Rata-rata nilai fitness tertinggi didapatkan dari penggunaan parameter maksimum generasi sebesar 50.

Tabel 4. Rata-rata Nilai Fitness untuk Jumlah Populasi

Crossover Rate	Rata-Rata Nilai Fitness pada Kontainer 20ft	Rata-Rata Nilai Fitness pada Mobil Box
50	0.524463333	0.7848375
75	0.523474167	0.790223333
100	0.531315833	0.7943125

Tabel 4 menunjukkan rata-rata nilai fitness untuk jumlah populasi yang didapatkan dari pengujian pada Kontainer 20ft dan Mobil Box. Rata-rata nilai fitness tertinggi didapatkan dari penggunaan parameter jumlah populasi sebesar 100.

Dari tabel 1 hingga 4 dapat disimpulkan bahwa nilai Crossover Rate terbaik adalah 0.7 (rata-rata nilai fitness = 0.531505 dan 0.7932025), nilai Mutation Rate terbaik adalah 0.2 (rata-rata nilai fitness = 0.531112778 dan 0.799757778), nilai Maksimum Generasi terbaik adalah 50 (rata-rata nilai fitness =

0.536595 dan 0.802015), nilai Jumlah Populasi terbaik adalah 100 (rata-rata nilai fitness = 0.531315833 dan 0.7943125).

• 3.3.    Pengujian Kinerja Algoritma Genetika

Pengujian ini dilakukan dengan membandingkan hasil dari algoritma genetika dengan dynamic programming. Hasil yang didapatkan dari pengujian dengan menggunakan Dynamic Programming adalah 0.54322 dengan terpilihnya 48 dari 90 barang pada kasus kontainer 20ft dan 0.84593 dengan terpilihnya 27 dari 90 barang pada kasus mobil box.

Hasil

[ Lemari Lemari Lemari Lemari Lemari Lemari Lemari i

Total [Berat, Ukuran] = [1910, 31962714]

Nilai Fitness =0.5432247456995408

Gambar 10. Hasil Dynamic Programming pada kasus kontainer 20ft

Gambar 10 menunjukkan hasil dari Dynamic Programming pada kasus kontainer 20ft. Dynamic Programming mendapatkan hasil nilai Fitness sebesar 0.54322 dengan terpilihnya 48 dari 90 barang.

Hasil

[ Kulkas Sofa Dispenser Dispenser Dispenser C

Total [BeraL Ukuran] = [554,4597099]

Nilai Fitness = 0.8459346739130432

Gambar 11. Hasil Dynamic Programming pada kasus mobil Box

Gambar 11 menunjukkan hasil dari Dynamic Programming pada kasus mobil box. Dynamic Programming mendapatkan hasil nilai Fitness sebesar 0.84593 dengan terpilihnya 27 dari 90 barang.

Hasil yang didapatkan dari Dynamic Programming merupakan hasil paling optimum yang bisa didapatkan jika dengan menggunakan data dummy tersebut. Hal ini dikarenakan Dynamic Programming yang mengecek secara keseluruhan seluruh kemungkinan kombinasi barang yang ada, sehingga hasilnya sudah dipastikan akan optimal. Jika dibandingkan antara hasil dari algoritma genetika yaitu 0.53879 dan 0.82552 dengan hasil dari dynamic programming, maka bisa disimpulkan bahwa algoritma genetika dapat menyelesaikan permasalahan knapsack problem 2 dimensi dengan cukup baik dikarenakan algoritma genetika dapat menghasilkan hasil sebesar 99% pada kasus kontainer 20ft dan 97.5% pada kasus mobil box dari hasil yang optimum yang didapatkan dari dynamic programming.

Pengujian selanjutnya adalah membandingkan waktu komputasi dari algoritma genetika dengan dynamic programming. Dalam pengujian ini, spesifikasi dari Hardware dan Software yang digunakan dapat dilihat pada tabel 5.

Tabel 5. Spesifikasi hardware dan software pengembang

Nama	Spesifikasi
Sistem Operasi	Microsoft Windows 10
Memori	8 GB
Penyimpanan	1TB
IDE	Apache NetBeans IDE 11.2

Dari pengujian tersebut, didapatkan hasil yaitu algoritma genetika memakan waktu sekitar kurang dari 0.2 detik sedangkan dynamic programming memakan waktu sekitar 37 hingga 40 detik. Dari hasil tersebut dapat disimpulkan bahwa algoritma genetika dapat menghasilkan hasil yang mendekati optimal dengan waktu komputasi yang jauh lebih cepat, sedangkan dynamic programming membutuhkan waktu yang lebih lama.

• 4.    Kesimpulan

Dilihat dari rata-rata nilai fitnessnya, maka dapat disimpulkan bahwa nilai Crossover Rate terbaik adalah 0.7 (rata-rata nilai fitness = 0.531505 dan 0.7932025), nilai Mutation Rate terbaik adalah 0.2 (rata-rata nilai fitness = 0.531112778 dan 0.799757778), nilai Maksimum Generasi terbaik adalah 50 (rata-rata nilai fitness = 0.536595 dan 0.802015), nilai Jumlah Populasi terbaik adalah 100 (rata-rata nilai fitness = 0.531315833 dan 0.7943125). Algoritma genetika dapat menghasilkan hasil dengan

Bramantya, dkk.

Rancangan dan Analisis Model Algoritma Genetika Untuk Menyelesaikan

Permasalahan Knapsack 2 Dimensi nilai fitness tertinggi sebesar yaitu 0.53879 dan 0.82552 yang jika dibandingkan dengan hasil dari dynamic programming, maka bisa disimpulkan bahwa algoritma genetika dapat menyelesaikan permasalahan knapsack problem 2 dimensi dengan cukup baik dikarenakan algoritma genetika dapat menghasilkan hasil sebesar 99% pada kasus kontainer 20ft dan 97.5% pada kasus mobil box dari hasil yang optimum yang didapatkan dari dynamic programming. Algoritma Genetika juga memakan waktu yang jauh lebih sedikit (kurang dari 0.2 detik) untuk mendapatkan hasil tersebut jika dibandingkan dengan dynamic programming (37 hingga 40 detik).

References

• [1]    K.D. KW, M. Fadhli, C. Sutanto, ” Penyelesaian Knapsack Problem Menggunakan Algoritma Genetika” Seminar Nasional Informatika (semnasIF), Vol 1, no 4. 2010.

• [2]    Y.D. Regita, K.A. Santoso, A. Kamsyakawuni, “Algoritma Elephant Herding Optimization: Permasalahan Multiple Constraints Knapsack 0-1”. Majalah Ilmiah Matematika dan Statistika, [S.l.], v. 18, n. 1, p. 13-22, 2018.

• [3]    R. Erama, R. Wardoyo. “Modifikasi Algoritma Genetika untuk Penyelesaian Permasalahan Penjadwalan Pelajaran Sekolah”. IJCCS, 8(2): 111-120. 2014.

• [4]    N. Marina, “Algoritma untuk Masalah Knapsack Multidimensi” Jurnal Ilmiah Teknologi dan Rekayasa, 22(3). Jakarta. 2017.

• [5]    Irmeilyana, P.B.J. Bangun, D. Pratamawati, W.H Septiani. “Penerapan Algoritma Dynamic Programming Pada Permasalahan Knapsack 0-1” SEMIRATA BKS PTN Bid. MIPA Indonesia Barat, Jambi, 2017.

• [6]    Aristoteles, Wardiyanto, A. Dwiastuti. “Evaluasi Kinerja Genetic Algorithm (GA) dengan Strategi Perbaikan Kromosom Studi Kasus: Knapsack Problem” Jurnal Komputasi Unila, vol 3, no 2. 2015.

• [7]    K. DeJong. “Analysis of the Behavior of a Class of Genetic Adaptive”. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA. 1975.

• [8]    J. Grefenstette. “Optimization of control parameters for genetic algorithms” IEEE Trans. Syst. Man Cybern, 16, 122–128. 1986.

404