Implementasi Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO) Untuk Klasifikasi Kanker Payudara

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Jurnal Elektronik Ilmu Komputer Udayana

Volume 10, No 4. May 2022

Implementasi Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO) Untuk Klasifikasi Kanker Payudara

I Made Satria Bimantara^a1, I Wayan Supriana^a2, Luh Arida Ayu Rahning Putri^a3, I Wayan Santiyasa^a4, Ngurah Agus Sanjaya ER^a5, Anak Agung Istri Ngurah Eka Karyawati^a6

^aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana Badung, Bali, Indonesia ¹satriabimantara@student.unud.ac.id ²wayan.supriana@unud.ac.id ³rahningputri@unud.ac.id ⁴santiyasa@unud.ac.id

⁵agus_sanjaya@unud.ac.id ⁶eka.karyawati@unud.ac.id

Abstrak

Kematian terbesar akibat kanker setiap tahun disebabkan oleh kanker payudara (KP). Salah satu penyebab tingginya angka kejadian KP adalah deteksi dini yang terhambat. Machine learning telah banyak dimanfaatkan untuk deteksi dini secara otomatis serta mengklasifikasikan jenis kanker. Metode klasifikasi yang dapat digunakan untuk mengklasifikasikan KP ke dalam KP jinak atau ganas adalah GLVQ. Kepekaan inisialisasi vektor bobot awal secara acak pada GLVQ berpengaruh pada hasil tingkat akurasi. Optimasi vektor bobot awal pada GLVQ dapat menggunakan metode optimasi seperti PSO. Data Breast Cancer Wisconsin Diagnostic Data Set digunakan dengan beberapa tahapan pengolahan data, yaitu penanganan pencilan dengan metode Winsorizing, normalisasi z-score, dan reduksi dimensi dengan PCA. Hasil optimasi vektor bobot yang ditunjukkan melalui nilai rata-rata fitness yang dihasilkan pada PSO dipengaruhi oleh perubahan parameter φ₁, φ₂, dan ω. Nilai rata-rata fitness tertinggi sebesar 0,91868 dihasilkan melalui kombinasi parameter φ₁ = 2,4, φ₂ = 2,1, dan ω = 0,6. Tingkat akurasi dan tingkat kesalahan hasil klasifikasi kanker payudara yang dihasilkan metode GLVQ dipengaruhi oleh perubahan parameter a dan n_w. Kombinasi a = 0,1, n_w = 5, epoch maksimum sebesar 100, dan toleransi kesalahan minimum sebesar 10^-6 menghasilkan nilai rata-rata akurasi tertinggi sebesar 0,956044. Performa PSO-GLVQ memberikan nilai akurasi, recall, dan F2-Score yang lebih tinggi dibandingkan GLVQ.

Kata Kunci: Generalized Learning Vector Quantization, Particle Swarm Optimization, optimasi vektor bobot, klasifikasi kanker payudara

• 1.    Pendahuluan

Kanker payudara merupakan tumor ganas yang menyerang jaringan payudara, yaitu kelenjar susu, saluran kelenjar susu, dan jaringan penunjang lainnya [1]. Kanker ini biasanya terjadi pada perempuan dan menjadi kanker paling umum nomor dua di dunia [1]. Delapan sampai sembilan persen wanita terkena kanker payudara menurut hasil survei yang dilakukan World Health Organization (WHO) [2]. Kanker payudara juga dapat diderita oleh pria, namun kemungkinan kejadian yang lebih rendah dibandingkan wanita [3].

Salah satu penyebab tingginya angka kejadian kanker payudara yaitu terhambatnya upaya deteksi dini kanker payudara [3]. Padahal, kemungkinan pasien sembuh menjadi lebih tinggi apabila jenis kanker diketahui sejak dini [4]. Deteksi dini terhadap tingkat keganasan kanker dapat menurunkan tingkat kematian pasien [5]. Keterlambatan deteksi dini terhadap pasien kanker payudara sebelum kanker mulai menjadi ganas dapat berujung pada kematian [6].

Machine learning sebagai hasil perkembangan teknologi dan ilmu pengetahuan dapat dimanfaatkan untuk melakukan pendeteksian dini secara otomatis [2]. Bidang kesehatan dan pengobatan yang membantu dokter dan ahli dalam mengklasifikasikan jenis kanker telah memanfaatkan klasifikasi berbasis machine learning [7]. Metode GLVQ merupakan salah satu metode dalam machine learning

Bimantara, dkk.

Klasifikasi Kanker Payudara Menggunakan Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO) yang bisa dimanfaatkan untuk melakukan klasifikasi. Metode ini memanfaatkan vektor bobot sebagai basis di dalam melakukan klasifikasi.

Sato dan Yamada memperkenalkan GLVQ pada tahun 1996 [8] sebagai variasi dan penyempurnaan dari algoritma Learning Vector Quantization (LVQ) khususnya pada LVQ2.1. Penelitian [8] menggunakan metode GLVQ untuk penerjemahan bahasa isyarat pada tahun 2020. Hasil penelitiannya menunjukkan bahwa GLVQ memberikan akurasi sebesar 71,37% pada nilai learning rate sebesar 0,9 dan lebih tinggi dibandingkan penelitian serupa yang dilakukan Hermawan [8] dengan menggunakan metode LVQ yang memperoleh nilai akurasi hanya 61,54%. Penelitian [9] menyatakan bahwa masalah konvergensi dan ketidakstabilan masih dimiliki metode LVQ yang dikemukakan oleh Kohonen. GLVQ sebagai pembelajaran LVQ modern dapat mencapai konvergen lebih cepat apabila dibandingkan dengan LVQ.

Kepekaan terhadap inisialisasi vektor bobot menjadi salah satu masalah utama dalam pembelajaran GLVQ [10]. Sejumlah vektor masukan yang diwakilkan oleh data latih dipilih secara langsung sebagai vektor bobot awal. Cara ini masih memiliki kelemahan karena data latih yang dipilih secara acak dan tidak tepat untuk dijadikan sebagai vektor bobot masukan menyebabkan hasil tingkat akurasi yang buruk [11]. Inisialisasi vektor bobot awal perlu dipilih yang optimasi karena vektor bobot menjadi acuan di dalam proses klasifikasi [12] dan mempengaruhi hasil klasifikasi [13]. Oleh karena itu, perlu dilakukan optimasi vektor bobot pada GLVQ untuk mendapatkan vektor bobot awal yang optimal sehingga diharapkan mendapatkan nilai akurasi yang lebih tinggi di dalam melakukan klasifikasi. Algoritma optimasi seperti Particle Swarm Optimization (PSO) bisa digunakan untuk hal tersebut [14].

Algoritma PSO memiliki beberapa keunggulan dibandingkan algoritma optimasi yang lainnya. Menurut Ridwansyah et al [15], permasalahan optimasi dapat diselesaikan menggunakan Algoritma PSO. Algoritma PSO memiliki keunggulan dari segi efisiensi apabila dibandingkan dengan metode optimasi yang lain [13]. Asriningtias mengungkapkan bahwa proses pelatihan neural network memiliki waktu lebih cepat apabila menggunakan Algoritma PSO daripada Algoritma Genetika. Kombinasi Neural Network dan Algoritma PSO terbukti dapat memberikan nilai akurasi yang lebih besar apabila dibandingkan hanya menggunakan neural network saja. Akurasinya bertambah sebesar 7,78% [15].

Penelitian ini memanfaatkan Algoritma PSO untuk mengoptimasi vektor bobot awal pada GLVQ sebelum diinisialisasi, sehingga tahap pelatihan pada GLVQ menggunakan vektor bobot awal yang optimal. Pengujian parameter terbaik dari GLVQ dan PSO dilakukan untuk mendapatkan kombinasi parameter terbaik dari keduanya dalam mengklasifikasikan kanker payudara. Pengujian untuk membandingkan hasil akurasi yang dihasilkan metode GLVQ dengan dan tanpa optimasi PSO dilakukan menggunakan sejumlah metriks performansi.

• 2.    Metode Penelitian
  
  2.1.  Data Penelitian

Data Breast Cancer Wisconsin (Diagnostic) Data Set yang didapat dari University of California Irvine (UCI) Machine Learning Repository digunakan sebagai data sekunder. Beberapa penelitian sebelumnya telah menggunakan data ini dengan teknik pengolahan data dan metode klasifikasi yang berbeda [16]. Data ini memiliki 569 baris data dengan 32 atribut. Rincian ke-32 atribut tersebut, yaitu ID, diagnosis, dan 30 atribut hasil komputasi sistem Xcyt. Atribut ID tidak memberikan informasi yang berarti karena hanya menunjukkan nomor unik setiap pasien yang menderita kanker payudara. Oleh karena itu, atribut ini tidak diikutkan ke dalam model [16]. Kondisi kanker payudara yang dialami pasien dari hasil pemeriksaan ditunjukkan melalui atribut diagnosis. Atribut ini menjadi label kelas pada data. Terdapat 357 baris data pasien yang mengidap kanker payudara jinak (benign) yang disimbolkan dengan “B” dan 212 baris data pasien yang mengidap kanker payudara ganas (malignant) yang disimbolkan dengan “M”.

• 2.2.    Desain Penelitian

Gambar 1 menunjukkan diagram alir penelitian. Penelitian diawali dengan membagi data penelitian menjadi data latih dan data uji menggunakan metode Holdout. Proporsi data latih dan data uji masing-masing sebesar 80% dan 20%. Data latih digunakan untuk: (i) menentukan kombinasi parameter GLVQ terbaik; (ii) menentukan kombinasi parameter PSO terbaik; (iii) mengoptimasi vektor bobot awal dengan PSO; dan (iv) proses pelatihan dengan PSO-GLVQ dan GLVQ, dengan menggunakan 5-fold crossvalidation. Perhitungan nilai akurasi dan tingkat kesalahan dari: (i) klasifikasi kanker payudara yang dihasilkan metode GLVQ menggunakan vektor bobot tanpa dioptimasi dengan PSO; dan (ii) klasifikasi

kanker payudara yang dihasilkan metode GLVQ menggunakan vektor bobot yang dioptimasi dengan PSO, menggunakan data uji.

Gambar 1. Diagram alir desain penelitian

Identifikasi dan penanganan data pencilan adalah tahapan preprocessing yang pertama. Metode Winsorizing digunakan untuk mengidentifikasi dan menangani data pencilan pada suatu atribut. Penelitian ini menggunakan threshold nilai k=5 untuk menentukan data pencilan pada suatu atribut [17]. Semua nilai yang berada di bawah persentil ke-5 (P5) diubah menjadi nilai pada P5, sedangkan semua nilai yang berada di atas persentil ke-95 (P95) diubah menjadi nilai pada P95[17]. Hal ini dilakukan untuk seluruh atribut yang ada.

Normalisasi data merupakan tahapan preprocessing yang kedua. Metode normalisasi z-score seperti persamaan (1) digunakan sebagai metode normalisasi data. Tahapan ini memiliki peran yang penting di dalam penambangan data, khususnya klasifikasi dan klasterisasi. Agar proses penambangan data tidak bias, nilai pada setiap atribut yang memiliki rentang berbeda perlu distandarisasi atau dinormalisasi [18].

x1

Xi - B

^B

( 1 )

Reduksi atribut atau dimensi merupakan tahapan preprocessing yang ketiga. Proses pelatihan model klasifikasi dapat berjalan lebih cepat dan tetap memberikan hasil yang optimal dengan melakukan reduksi dimensi pada data. Metode Principal Component Analysis (PCA) diterapkan untuk melakukan reduksi dimensi pada penelitian ini. Metode ini memilih sejumlah k komponen utama (KU). Sejumlah k KU yang didapat selanjutnya digunakan untuk mereduksi atribut awal pada data penelitian ke dalam ranah baru. Kumulatif proporsi nilai variansi yang dihasilkan dari setiap komponen akan digunakan untuk memilih sejumlah k KU. Penelitian ini menggunakan threshold nilai minimum kumulatif proporsi variansi yang bisa dijelaskan sebesar 80% [19] dalam menentukan sejumlah k KU yang dipertahankan. Data latih yang sudah di-preprocessing kemudian digunakan pada tahapan tuning parameter dari metode GLVQ. Tahapan ini menggunakan metode Grid Search dengan validasi 5-fold cross-validation. Lima nilai akurasi diperoleh untuk setiap kombinasi parameter GLVQ yang dihasilkan dari lima eksperimen yang dilakukan. Eksperimen ke-i adalah melatih model GLVQ menggunakan seluruh data latih selain data pada fold ke-i; kemudian mengevaluasi model tersebut menggunakan data pada fold ke-i. Kelima nilai akurasi ini kemudian digunakan untuk mendapatkan nilai rata-rata akurasi untuk setiap kombinasi parameter GLVQ. Kombinasi parameter optimal dari metode GLVQ yang menghasilkan nilai rata-rata akurasi tertinggi adalah luaran dari tahapan ini.

Data latih yang sudah di-preprocessing serta kombinasi parameter optimal dari metode GLVQ digunakan pada tahapan tuning parameter dari metode PSO. Tahapan ini menggunakan metode Grid Search dengan validasi 5-fold cross-validation. Lima nilai fitness diperoleh untuk setiap kombinasi parameter PSO yang dihasilkan dari lima eksperimen yang dilakukan. Eksperimen ke-i adalah mengoptimasi vektor bobot awal dengan seluruh data latih selain data pada fold ke-i; kemudian menghitung nilai fitness dari vektor bobot awal yang sudah dioptimasi menggunakan data pada fold kei. Kelima nilai fitness ini kemudian digunakan untuk mendapatkan nilai rata-rata fitness untuk setiap kombinasi parameter PSO. Kombinasi parameter optimal dari metode PSO yang menghasilkan nilai rata-rata fitness tertinggi adalah luaran dari tahapan ini.

Kombinasi parameter optimal dari GLVQ dan PSO yang telah didapat dari tahapan sebelumnya kemudian digunakan pada tahap pelatihan GLVQ. Terdapat dua cara inisialisasi vektor bobot pada tahap ini, yaitu menggunakan vektor bobot awal yang diinisialisasi secara acak dan menggunakan vektor bobot awal yang dioptimasi dengan Algoritma PSO. Fungsi pembangkit acak berdistribusi uniform dalam rentang -1 sampai 1 [9] digunakan untuk menginisialisasi vektor bobot awal secara acak, sedangkan Algoritma PSO digunakan untuk mengoptimasi vektor bobot awal. Setelah vektor bobot awal dipastikan sudah diinisialisasi, baik menggunakan PSO atau secara acak, proses dilanjutkan dengan pelatihan menggunakan algoritma pelatihan GLVQ. Luaran dari proses ini adalah dua model pengklasifikasi yang sudah dilatih, yaitu PSO-GLVQ dan GLVQ.

Bimantara, dkk.

Klasifikasi Kanker Payudara Menggunakan Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO)

Tahap klasifikasi atau pengujian GLVQ dilakukan setelah dua model pengklasifikasi hasil pelatihan didapatkan. Tahap ini dilakukan untuk mengevaluasi performa dari kedua model pengklasifikasi tersebut menggunakan data uji. Confusion matrix digunakan untuk merepresentasikan hasil klasifikasi dari kedua model. Evaluasi model PSO-GLVQ dan GLVQ menggunakan sejumlah ukuran performa, seperti accuracy, error rate, recall, precision, dan F2-Score dihitung berdasarkan confusion matrix masing-masing.

• 2.3.    Tahapan PSO Untuk Optimasi Vektor Bobot Pada GLVQ

Penelitian [13] digunakan sebagai acuan pada tahap optimasi vektor bobot menggunakan Algoritma PSO. Vektor bobot awal pada GLVQ dioptimasi menggunakan Algoritma PSO. Vektor bobot optimal diperoleh dari Gbest pada iterasi terakhir. Vektor bobot yang sudah dioptimasi selanjutnya digunakan pada proses pelatihan GLVQ. Adapun langkah-langkah di dalam Algoritma PSO [13]:

1.

2.

2.a

2.b

Tentukan data latih, jumlah partikel sebagai Np, maksimum iterasi sebagai E, laju belajar kecerdasan individu (cognition) sebagai φ₁, laju belajar hubungan sosial antar individu sebagai φ₂, dan dua bilangan acak (dalam interval 0 – 1) masing-masing r1 dan r2.

Lakukan langkah 2.a – 2.g sebagai tahap inisialisasi awal.

Tentukan batas minimum sebagai T_min dan batas maksimum sebagai T_max untuk setiap atribut.

Tentukan kecepatan minimum sebagai V_min dan kecepatan maksimum sebagai V_max untuk setiap atribut. Nilai V_min sama dengan -V_max dan nilai V_max dapat ditentukan oleh user [20]. Nilai v_max dapat ditentukan dengan memperhatikan rentang nilai dari setiap atribut yang ada [20], sehingga V_max dan V_min masing-masing dapat ditentukan menggunakan persamaan (2) dan (3).

^Vmax(J)    (T_max(jy

^Vmin(J)    ^—Vmax(j)

-

Tmin(J))

( 2 )

( 3 )

• 2.c Inisialisasi kecepatan awal seluruh partikel dengan nilai 0.

• 2.d Inisialisasi posisi awal seluruh partikel dengan menggunakan persamaan (4).

^xij     ^Tmin(j) ^{+ ran}d[0,1] × (Tmax(J)   ^Tmin(j))

( 4 )

• 2.e Inisialisasi nilai fitness seluruh partikel dengan nilai 0.

• 2.f Inisialisasi Pbest awal setiap partikel dengan masing-masing posisi awal setiap partikel yang telah diinisialisasi.

• 2.g Inisialisasi Gbest awal dengan Pbest dari partikel dengan nilai fitness tertinggi.

  3.

  
  

  4.

  
  

  4.a (i) (ii)

  
  

  Atur nilai iter₀ sama dengan nol.

  Selama nilai iter_t kurang dari E, lakukan langkah 4.a - 4.d.

  Untuk setiap partikel, lakukan:

  Hitung nilai fitness partikel menggunakan persamaan (10); dan

  Perbarui nilai Pbest dengan memperhatikan nilai fitness pada iterasi ke-iter_t-1 dan nilai fitness pada iterasi ke-iter_t. Jika nilai fitness partikel pada iterasi ke-iter_t lebih baik dibandingkan nilai fitness pada iterasi ke-iter_t-1, maka kondisi partikel pada iterasi ke-1 akan menjadi Pbest yang baru dari partikel tersebut dan begitupun sebaliknya. Pembaruan nilai Pbest menggunakan persamaan (5) berikut.

  
  

  Pbestt⁺¹ = {

  
  

  Pbestt, fitness(χt⁺¹) ≤ fitness(Pbest^t_i^

  
  

  x_i⁺¹, fitness(χt⁺¹) > fitness(Pbestt)

  
  

  ( 5 )

  
  

• 4.b Pilih partikel dengan nilai fitness paling maksimum dari semua partikel yang ada, kemudian jadikan sebagai Gbest sesuai dengan persamaan (6).

  Gbest^t+1 = {

  
  

Gbest^t, ar gmax(fitness(Pbest^t_i⁺¹y) ≤ fitness(Gbest^t)

Pbest^t_i⁺¹, ar gmax(f itness(Pbest^t_i⁺¹)) > fitness(Gbest^t)

( 6 )

4.c Untuk setiap partikel, lakukan:

• (i)    Perbarui kecepatan menggunakan persamaan (7); dan

v_i+¹ = ω× v_ij + φ₁×r₁× (Pbest_ij - x_ijj + φ₂×r₂× (Gbestj - xjjj =

(^vmaxj)' Vij  ≥ ^vmaxj)

^vminj)∣ ^vij  ≤ ^vmin(j)

^vij , ^vminj) < Vij  < ^vmaxj)

( 7 )

• (ii)    Perbarui posisi menggunakan persamaan (8).

(Tmax(j)’ ^xij  ≥ Tmaxfj)

^t+¹ < T ■ _r-' ⁱ mmj)> ^xij  ≤ ⁱminj)

^xij ’ Tminj) < ^xij < Tmaxj)

( 8 )

• 4.d    Perbarui nilai iter_t+1 menggunakan persamaan (9).

iter_t+1 = iter_t + 1

( 9 )

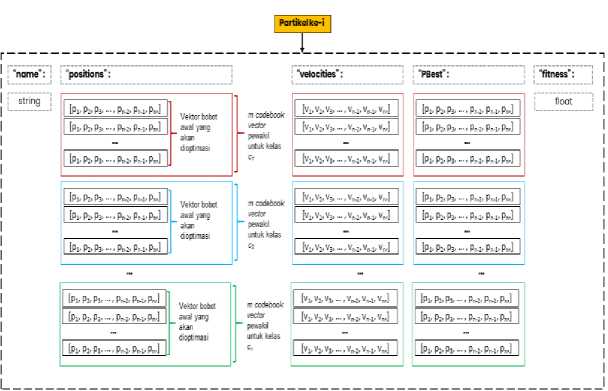
Gambar 2. Ilustrasi satu partikel yang diinisialisasi untuk proses optimasi vektor bobot awal pada GLVQ

• 2.4.    Perhitungan Nilai Fitness Partikel

Data latih digunakan pada proses optimasi vektor bobot awal pada PSO, sehingga fungsi objektif pada kasus optimasi PSO ini adalah memaksimumkan jumlah data latih yang terklasifikasi benar oleh suatu vektor bobot (yang diwakili satu partikel). Fungsi fitness sesuai persamaan (10) digunakan untuk menghitung nilai fitness partikel berdasarkan fungsi objektif yang telah ditetapkan. Perhitungan nilai fitness setiap partikel mengikuti tahapan-tahapan sebagai berikut [12]:

• 1.    Masukan data latih beserta dengan label kelasnya. Misalkan label kelas hasil klasifikasi dari data latih ke-i yaitu C_i.

• 2.    Lakukan perhitungan jarak antara data latih dengan setiap vektor bobot dalam satu partikel menggunakan persamaan (12). Misalkan Dj merupakan jarak antara vektor bobot ke-j dengan data latih ke-i.

• 3.    Label kelas hasil klasifikasi untuk data latih ke-i dapat ditentukan dari nilai terkecil yang diperoleh pada hasil perhitungan jarak nomor 2. Misalkan T_i merupakan label kelas hasil klasifikasi untuk data latih ke-i.

• 4.  Nilai fault diperbarui dengan syarat: (a) Jika T_i ≠ C_i, maka nilai fault bertambah satu dari nilai

sebelumnya; dan (b) Jika T_i = C_i, maka nilai fault tidak berubah dari nilai sebelumnya.

• 5.  Hitung nilai fitness partikel dengan persamaan (10). F_i merupakan fitness partikel ke-i, N_latih

merupakan jumlah seluruh baris data latih, dan fault merupakan jumlah seluruha baris data latih yang terklasifikasi salah dari kelas target aslinya.

Fi

_ Ulatih - fault

^Nlatih

( 10 )

Bimantara, dkk.

Klasifikasi Kanker Payudara Menggunakan Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO)

• 2.5.    Tahapan Pelatihan Menggunakan GLVQ

Suatu data masukan dapat dikenali melalui vektor bobot yang sudah dilatih dengan metode GLVQ, sehingga bisa diklasifikasikan ke luaran yang tepat. Tahapan pelatihan menggunakan GLVQ adalah sebagai berikut [9].

• 1.  Inisialisasi sampel data latih V= {v_i ∈ Kⁿ,i = 1,.,m}.

• 2.  Masukkan nilai maksimum epoch sebagai T dan nilai laju pembelajaran sebagai α₀.

• 3.    Inisialisasi vektor bobot awal sebagai W = {wj ∈ ^ⁿJ = 1,..,m} secara acak. Apabila dilakukan optimasi terhadap vektor bobot dengan PSO, maka gunakan vektor bobot hasil optimasi PSO sebagai vektor bobot awal dalam pelatihan GLVQ.

• 4.    Inisialisasi nilai t = 0.

• 5.    Selama kondisi berhenti belum tercapai, lakukan langkah 5.a sampai 5.b.

• 5 .a Hitung nilai laju pembelajaran dengan persamaan (11).

a = a0(1^- -)                                                                            ( n )

5.b Untuk setiap sampel data latih v_l dan W, lakukan langkah 5.b.1 sampai 5.b.4.

• 5 .b.1 Hitung jarak v_i dengan setiap w_j∙ pada W menggunakan persamaan (12) dan tentukan w+ dan w^-.

Il^vi ^{- w}jh = ∑ⁿ=1(^vi,k ^{- w}j,k)                                                                           ( 12 )

5.b.2

5.b.3

Tentukan d⁺(v_i) dan d^-(v_i~).

Hitung perbedaan jarak relatif μ(v_i^) sesuai dengan persamaan (13).

μ(v^ = ^d⅛) ^-d-(v_i) ∈ [—1,1] ⁱ^      d⁺(v_i) + d^-(v_i)     ^{l , j}

( 13 )

5.b.4

W⁺ ^

W^- ^

Lakukan perbaikan w⁺ dan w^-

_{+  l}     Sf        d^-(v_i)

^{w+ +}  ■          ■   +  ■

_-        Sf       d⁺(v_i)

^{w     a} ■,-■-.■  -

masing-masing menggunakan persamaan (14) dan (15).

w⁺)

w^-)

( 14 )

( 15 )

• 6.    Luaran proses pelatihan adalah W = {w_j ∈ Nⁿ,j = 1, ...,m} sebagai vektor bobot hasil pelatihan.

Kondisi berhenti pada pembelajaran vektor bobot sesuai algoritma di atas yaitu apabila nilai maksimum epoch telah tercapai [21] atau perubahan nilai vektor bobot iterasi ke-t dibandingkan hasil iterasi ke-(t - 1) kurang dari toleransi perubahan [22].

• 2.6.    Tahapan Klasifikasi Menggunakan GLVQ

Vektor bobot hasil pelatihan menggunakan metode PSO-GLVQ dan GLVQ selanjutnya akan masuk ke tahap klasifikasi dengan menggunakan GLVQ. Tahapan klasifikasi menggunakan GLVQ adalah sebagai berikut [9].

1.

2.

2.a

2.b

Masukkan himpunan vektor bobot sebagai W dan himpunan data uji sebagai V.

Untuk setiap v_i ∈V lakukan langkah 2.a sampai 2.c.

Hitung d(v_i, w_j) sesuai persamaan (12) untuk setiap w_j ∈ W.

Cari indeks dari w_j yang memiliki jarak paling minimum dengan v_i sesuai persamaan (16).

s(v_i) = argminj=₁....._m d(v_i, wj)

( 16 )

2.c Kelas dari v_i dapat ditentukan oleh c(w_s(Vi) ).

Luaran proses ini adalah hasil klasifikasi dari setiap v_i ∈ V dengan metode GLVQ.

• 2.7.    Evaluasi dan Seleksi Model Klasifikasi

Pemilihan kombinasi parameter optimal dari metode GLVQ dan PSO menggunakan data latih yang sudah di-preprocessing. Proses tersebut menggunakan metode Grid Search dengan validasi 5-fold cross-validation. Pelatihan model PSO-GLVQ dan GLVQ dilakukan dengan keseluruhan data latih yang sama menggunakan kombinasi parameter optimal dari kedua metode ini. Evaluasi PSO-GLVQ dan GLVQ dilakukan dengan menggunakan data uji yang sama yang sudah di-preprocessing. Confusion matrix digunakan untuk merepresentasikan hasil klasifikasi kedua model pengklasifikasi tersebut. Confusion matrix ini selanjutnya digunakan sebagai acuan dalam menghitung sejumlah ukuran evaluasi model pengklasifikasi. Tabel 1 merupakan ilustrasi confusion matrix yang digunakan pada penelitian ini.

Tabel 1. Confusion matrix untuk mengevaluasi model pengklasifikasi PSO-GLVQ dan GLVQ

	Kelas hasil klasifikasi		Jumlah
	Malignant	Benign
Malignant Kelas Aktual	TP	FN	P
Benign	FP	TN	N
Jumlah	P’	N’

• 3.    Hasil dan Pembahasan
  
  3.1.    Hasil Implementasi Tahap Pengolahan Data

Data latih dan data uji dibagi dari data penelitian pada awal tahap tahap pengolahan data. Terdapat 455 baris data untuk data latih dan 114 baris data untuk data uji. Terdapat 281 baris data teridentifikasi sebagai data pencilan untuk ke-30 atribut yang diidentifikasi dari 455 baris data pada data latih. Data latih yang sudah ditangani data pencilannya kemudian dinormalisasi dengan metode z-score. Metode PCA kemudian digunakan untuk mereduksi atribut pada data latih yang sudah dinormalisasi. Berdasarkan hasil perhitungan variance, proporsi variance, dan kumulatif proporsi variance yang bisa dijelaskan dari ke-30 komponen yang terbentuk dari data latih, sejumlah empat principal component (PC) pertama dapat dipilih untuk mereduksi atribut. Empat PC dapat menjelaskan variance dari data latih sebesar 81,0492%.

• 3.2.    Pengaruh Perubahan Parameter Pada GLVQ Terhadap Hasil Akurasi

Pengujian pengaruh perubahan parameter-parameter pada GLVQ, yaitu a (laju pembelajaran) dan n_w (jumlah vektor bobot per kelas) menggunakan data latih yang sudah di-preprocessing. Pengujian ini menggunakan metode Grid search dengan validasi 5-fold cross-validation. Himpunan parameter a {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9} [8] dan himpunan parameter n_w {1,2, 3, 4, 5} [9] digunakan pada pengujian ini. Nilai epoch maksimum (maxepoch) ditetapkan sebesar 100 dan toleransi kesalahan minimum (minerror) ditetapkan sebesar 10^-6. Nilai maxepoch sebesar 100 dapat menghasilkan akurasi tertinggi dengan waktu komputasi yang lebih singkat dibandingkan nilai epoch maksimum yang berada dalam rentang 100 sampai 1000 [23]. Nilai minerror sebesar 10^-6 digunakan berdasarkan penelitian [21] yang menyatakan bahwa nilai akurasi yang dihasilkan tidak dipengaruhi oleh toleransi kesalahan minimum. Dari keseluruhan anggota himpunan untuk setiap parameter pada GLVQ, sejumlah 45 kombinasi parameter dihasilkan berdasarkan skema Grid Search. Kombinasi parameter pada GLVQ yang menghasilkan nilai rata-rata akurasi tertinggi dapat ditentukan dari keseluruhan hasil kombinasi parameter beserta nilai akurasi pada setiap fold.

Tabel 2. Cuplikan hasil kombinasi parameter pada GLVQ beserta nilai akurasi yang dihasilkan menggunakan metode Grid Search dengan validasi 5-fold cross-validation

nw	a.	Akurasi Fold-1	Akurasi Fold-2	Akurasi Fold-3	Akurasi Fold-4	Akurasi Fold-5	Rata-rata akurasi
1	0,1	0,9560	0,9341	0,9121	0,9341	0,9341	0,9341
1	0,2	0,9560	0,9341	0,9231	0,9341	0,9451	0,9385
1	0,3	0,9560	0,9341	0,9231	0,9341	0,9451	0,9385
1	0,4	0,9560	0,9341	0,9231	0,9341	0,9451	0,9385
1	0,5	0,9560	0,9341	0,9231	0,9341	0,9451	0,9385
…5	0…,6	0,9…890	0,9341	0,9121	0,9451	0,9560	0,9473
5	0,7	0,9780	0,9341	0,9121	0,9451	0,9670	0,9473
5	0,8	0,9890	0,9341	0,9121	0,9451	0,9451	0,9451

Bimantara, dkk.

Klasifikasi Kanker Payudara Menggunakan Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO)

5   0,9  0,9780   0,9341    0,9121    0,9451    0,9560      0,9451

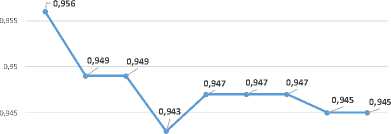
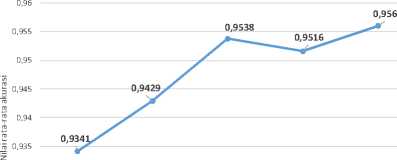
Kombinasi parameter pada GLVQ, yaitu α=0,1, n_w=5, maxepoch =100, dan minerror=10-⁶ adalah kombinasi parameter optimal dari GLVQ berdasarkan keseluruhan hasil pengujian. Nilai rata-rata akurasi sebesar 0,956043 dihasilkan dengan kombinasi ini. Nilai rata-rata tingkat akurasi pada hasil klasifikasi kanker payudara memiliki kecenderungan menurun apabila parameter α semakin besar yang dijelaskan melalui Gambar 3. Semakin kecil parameter a, maka vektor bobot semakin cepat konvergen pada tahap pelatihan yang berpengaruh terhadap hasil klasifikasi, begitupun sebaliknya [21]. Nilai rata-rata tingkat akurasi pada hasil klasifikasi kanker payudara memiliki kecenderungan meningkat apabila parameter n_w semakin besar yang dijelaskan melalui Gambar 4. Semakin besar parameter n_w artinya semakin banyak jumlah vektor bobot pewakil di setiap kelas yang ada. Jumlah vektor bobot pewakil di setiap kelas yang semakin banyak dapat memberikan ruang solusi yang lebih besar ketika vektor bobot berlatih dengan data latih. Nilai parameter n_w dibuat meningkat pada penelitian ini karena kesalahan generalisasi dari model GLVQ dapat diminimalkan dengan konfigurasi parameter n_w yang besar [9]. Kemampuan generalisasi dan ketangguhan dari model GLVQ meningkat seiring parameter n_w membesar [24].

0,96

0,94

0,93

0,925

0,935

0,1          0,2          0,3         0,4         0,5          0,6         0,7         0,8          0,9

Laju Pembelajaran

0,92

12345

Jumlah vektor bobot per kelas

Gambar 3. Grafik pengaruh perubahan parameter a terhadap nilai rata-rata tingkat akurasi hasil klasifikasi kanker payudara

Gambar 4. Grafik pengaruh perubahan parameter ∏_w terhadap nilai rata-rata tingkat akurasi hasil klasifikasi kanker payudara

• 3.3.    Pengaruh Perubahan Parameter Pada PSO Terhadap Hasil Optimasi Vektor Bobot

Pengujian pengaruh perubahan parameter-parameter pada PSO yaitu φ₁, φ₂ dan ω menggunakan data latih yang sudah di-preprocessing dan kombinasi parameter optimal GLVQ dari pengujian sebelumnya. Metode Grid Search dengan validasi 5-fold cross-validation digunakan pada pengujian ini untuk melihat pengaruh perubahan parameter-parameter pada PSO terhadap hasil optimasi vektor bobot (yang ditunjukkan melalui nilia rata-rata fitness) untuk klasifikasi kanker payudara. Himpunan parameter φ₁ dan φ₂ yang digunakan masing-masing yaitu {2.1, 2.2, 2.3, 2.4, 2.5}. Himpunan parameter ω yang digunakan yaitu {0.5, 0.6, 0.7, 0.8, 0.9, 1.0} [14]. Parameter lain pada PSO seperti jumlah partikel (N_p) dan jumlah iterasi maksimum (E_max) nilainya dibuat tetap masing-masing sebesar 30 [20] dan 100 [12]. Dari keseluruhan anggota himpunan untuk setiap parameter pada PSO, sejumlah 150 kombinasi parameter dihasilkan berdasarkan skema Grid Search. Kombinasi parameter pada PSO yang menghasilkan nilai rata-rata fitness teritinggi dapat ditentukan dari keseluruhan hasil kombinasi parameter beserta nilai fitness pada setiap fold.

Tabel 3. Cuplikan hasil kombinasi parameter pada PSO beserta nilai fitness yang dihasilkannya dengan metode validasi 5-fold cross-validation

φι	φ2	ω	Fitness Fold-1	Fitness Fold-2	Fitness Fold-3	Fitness Fold-4	Fitness Fold-5	Rata-rata fitness
2,1	2,1	0,5	0,8681	0,8791	0,8132	0,9121	0,8681	0,8681
2,1	2,1	0,6	0,8462	0,8571	0,8352	0,8462	0,7802	0,8330
2,1	2,1	0,7	0,8462	0,9231	0,7473	0,8681	0,9011	0,8571
2,1	2,1	0,8	0,8681	0,8132	0,8791	0,8132	0,8681	0,8484
2,1	2,1	0,9	0,8462	0,8132	0,9341	0,7363	0,8462	0,8352
2…,5	2,5	0…,7	0,8…022	0,8901	0,8901	0,8132	0,9231	0,8637
2,5	2,5	0,8	0,9231	0,9121	0,8242	0,8352	0,7253	0,8440
2,5	2,5	0,9	0,8352	0,8681	0,8352	0,9121	0,8352	0,8571
2,5	2,5	1	0,7692	0,9341	0,7912	0,8571	0,8681	0,8440

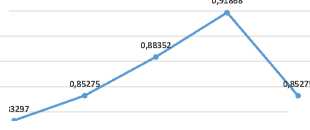
Kombinasi parameter pada PSO, yaitu φ₁=2,4, φ₂=2,1, ω=0,6, E_max=100, dan N_p=30 adalah kombinasi parameter optimal dari PSO berdasarkan keseluruhan hasil pengujian. Nilai rata-rata fitness tertinggi sebesar 0,91868 dihasilkan dengan kombinasi ini. Kombinasi parameter optimal GLVQ dari hasil pengujian sebelumnya, yaitu n_w sebesar 5 digunakan pada tahap pengujian parameter PSO untuk membentuk struktur partikel yang diinisialisasi.

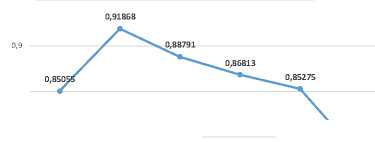
Ketika parameter φ₁ berubah dalam interval 2,1 sampai 2,4, maka nilai rata-rata fitness memiliki kecenderungan meningkat, walaupun terjadi penurunan nilai rata-rata fitness ketika parameter φ₁ lebih dari 2,4. Hal ini dijelaskan melalui grafik pada Gambar 5. Partikel sulit menemukan solusi vektor bobot yang optimal ketika laju belajar komponen cognition yang semakin kecil. Hal ini dapat terbukti dengan nilai rata-rata fitness terendah saat parameter φ₁ sama dengan 2,1. Laju belajar komponen cognition sebesar 2,4 menjadi batas optimal pada penelitian ini. Nilai rata-rata fitness yang dihasilkan menurun apabila nilai parameter φ₁ lebih dari 2,4.

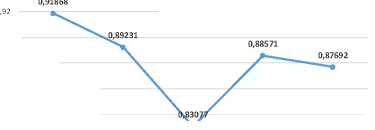
Ketika parameter φ₂ berubah dalam interval 2,1 sampai 2,5, maka nilai rata-rata fitness memiliki kecenderungan menurun, walaupun terjadi kenaikan nilai rata-rata fitness ketika parameter φ₂ berubah dari 2,3 menjadi 2,4. Hal ini dijelaskan melalui grafik pada Gambar 6. Partikel cenderung menemukan solusi vektor bobot yang optimal ketika laju belajar komponen sosial yang semakin kecil, begitupun sebaliknya. Hal ini dapat terbukti dengan nilai rata-rata fitness tertinggi saat parameter φ₂ sama dengan 2,1. Hasil optimasi vektor bobot yang optimal dihasilkan dari kombinasi parameter laju belajar komponen cognition yang lebih besar dari laju belajar komponen sosial pada penelitian ini.

Parameter ω sebesar 1,0 memberikan nilai rata-rata fitness terendah. Ketika parameter ω semakin besar, maka nilai rata-rata fitness cenderung menurun, walaupun terjadi kenaikan nilai rata-rata fitness ketika parameter ω berubah dari 0,5 menjadi 0,6. Kecepatan partikel diperbarui menggunakan persamaan (17) ketika parameter ω bernilai 1,0, sehingga tidak ada faktor pengontrol kelembaman partikel. Ketika kecepatan partikel diperbarui menggunakan persamaan (17), maka sekumpulan partikel cenderung terjebak pada optimum lokal [20]. Gambar 7 menampilkan hasil yang senada. Solusi vektor bobot lain yang berpotensi memberikan nilai fitness yang lebih baik dari 0,77802 tidak berhasil ditemukan oleh sekumpulan partikel.

vij1 = vtj + φ1×r1× (Pbest-j - xt^ + φ2 × r 0,94 0,91868 0,92 0,9 0,88352 0,88 0,86                        0,85275                                             0,85275 0,84      0,83297 0,82 0,8 0,78 2,1                 2,2                 2,3                 2,4                 2,5 Parameter Phi1 (Laju belajar cognition) Gambar 5. Grafik pengaruh perubahan parameter φ1 terhadap hasil optimasi vektor bobot menggunakan PSO 0,95 0,91868 0,9                                   0,88791 0,86813 0,85055                                              0,85275 0,85 0,8 0,77802 0,75 0,7 0,5              0,6             0,7              0,8              0,9               1 Parameter Inertia Gambar 7. Grafik pengaruh perubahan parameter ω terhadap hasil optimasi vektor bobot menggunakan PSO

2 × (Gbestt - χtj)                                 ( 17 ) 0,94 0,91868 0,92 0 9                        0,89231 ,                                                            0,88571 0,87692 0,88 0,86 0,84                                         0,83077 0,82 0,8 0,78 2,1                   2,2                   2,3                   2,4                   2,5 Parameter Phi2 (Laju belajar komponen sosial) Gambar 6. Grafik pengaruh perubahan parameter φ2 terhadap hasil optimasi vektor bobot menggunakan PSO

Bimantara, dkk.

Klasifikasi Kanker Payudara Menggunakan Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO)

• 3.4.    Perbandingan Hasil Klasifikasi PSO-GLVQ dan GLVQ

Hasil perbandingan metode PSO-GLVQ dan GLVQ menggunakan sejumlah ukuran evaluasi model klasifikasi disajikan seperti pada Tabel 4. Algoritma PSO yang digunakan untuk mengoptimasi vektor bobot awal pada GLVQ menghasilkan kinerja yang lebih baik jika dibandingkan dengan vektor bobot yang diinisialisasi secara acak. Tingkat akurasi pada data uji yang dihasilkan PSO-GLVQ yaitu 0,938596. Nilai ini lebih tinggi sebesar 0,008771 dari GLVQ yang memberikan tingkat akurasi sebesar 0,929825. Tingkat kesalahan pada data uji yang dihasilkan PSO-GLVQ yaitu 0,061404. Nilai ini lebih rendah apabila dibandingkan hasil yang dihasilkan metode GLVQ, yaitu sebesar 0,070175.

Tabel 4. Hasil perbandingan ukuran evaluasi antara metode GLVQ dan PSO-GLVQ untuk klasifikasi kanker payudara

Model	TP	TN	FN	FP	Accuracy	Error rate	Recall	Precision	F2-Score
PSO-GLVQ	35	72	0	7	0,938596	0,061404	1	0,83333	0,961538
GLVQ	36	70	2	6	0,929825	0,070175	0,947368	0,857143	0,927835

Kualitas dari metode PSO-GLVQ dan GLVQ dalam mengklasifikasikan data uji kanker payudara perlu diukur dengan ukuran selain accuracy dan error rate. Model pengklasifikasi dapat memberikan hasil yang bias ketika model dilatih menggunakan data yang imbalanced class dan diukur hanya dengan ukuran accuracy. Hal tersebut dikarenakan model pengklasifikasi memberikan keberhasilan yang rendah dalam mengklasifikasikan kelas minoritas, namun memberikan keberhasilan yang tinggi dalam mengklasifikasikan kelas mayoritas [25]. Ukuran recall, precision [10], dan F2-score [25] dapat digunakan untuk mengetahui kinerja model ketika dilatih menggunakan data dengan imbalanced class pada permasalahan klasifikasi biner.

Data dari kelas minoritas mengandung lebih banyak informasi yang berguna, sehingga keberhasilan model pengklasifikasi mengidentifikasi kelas minoritas lebih penting apabila dibandingkan dengan kelas mayoritas [25]. Oleh karena itu, pada kasus klasifikasi data medis ukuran evaluasi recall lebih diperhatikan [25]. Nilai FN berusaha diminimumkan oleh model pengklasifikasi kanker payudara yang dikembangkan. Sangat fatal apabila pasien yang seharusnya mengidap kanker payudara ganas diklasifikasikan sebagai pasien dengan kanker payudara jinak oleh model pengklasifikasi (nilai FN semakin besar). Pasien dengan kanker payudara jinak yang diklasifikasikan oleh model pengklasifikasi sebagai pasien dengan kanker payudara ganas lebih bisa ditoleransi apabila dibandingkan dengan kasus sebelumnya, walaupun tetap model pengklasifikasi sebisa mungkin meminimumkan kedua tipe kesalahan ini.

Metode PSO-GLVQ menghasilkan recall yang sempurna, yaitu sebesar satu (100%), sedangkan metode GLVQ menghasilkan 0,947368. Selisih recall keduanya sebesar 0,052632. PSO-GLVQ berhasil memberikan label positif pada seluruh baris data uji yang memang berlabel positif secara sempurna. Metode GLVQ menghasilkan precision sebesar 0,857143, sedangkan metode PSO-GLVQ menghasilkan precision sebesar 0,83333. F2-score dari metode PSO-GLVQ dan GLVQ dihitung dengan memperhatikan nilai recall dan precision yang dihasilkan masing-masing metode. Metode PSO-GLVQ menghasilkan F2-score sebesar 0,961538. Nilai ini lebih tinggi apabila dibandingkan dengan metode GLVQ yang menghasilkan F2-score sebesar 0,927835. Selisih F2-score keduanya sebesar 0,033703.

• 4.    Kesimpulan

Kombinasi parameter optimal dari PSO φ₁ = 2,4, φ₂ = 2,1, dan ω = 0,6 menghasilkan nilai rata-rata fitness tertinggi sebesar 0,91868 dengan validasi 5-fold cross-validation. Kombinasi parameter optimal dari GLVQ a = 0,1, n_w = 5, epoch maksimum sebesar 100, dan toleransi kesalahan minimum sebesar 10^-6 menghasilkan nilai rata-rata tingkat akurasi tertinggi sebesar 0,956044 dengan validasi 5-fold cross-validation. Kedua kombinasi parameter optimal dari PSO dan GLVQ digunakan membentuk model PSO-GLVQ dan GLVQ. Performa accuracy, error rate, recall, dan F2-score model PSO-GLVQ lebih baik jika dibandingkan metode GLVQ pada 20% data uji yang telah ditetapkan. Model PSO-GLVQ memberikan accuracy, error rate, recall, dan F2-score masing-masing sebesar 0,938596, 0,061404, 1, 0,961538. Model GLVQ memberikan accuracy, error rate, recall, dan F2-score masing-masing sebesar 0,929825, 0,070175, 0,947368, 0,927835.

References

• [1]    N. P. D. Rakasiwi, G. B. Setiawan, and I. G. N. W. Aryana, “Karakteristik Kanker Payudara

Dengan Metastasis Tulang Tahun 2015-2017 Di RSUP Sanglah Denpasar,” JURNAL MEDIKA UDAYANA, vol. 9, no. 1, pp. 17–22, Jan. 2020, doi: 10.24843.MU.2020.V9.i1.P04.

• [2]    F. S. Nugraha, M. J. Shidiq, and S. Rahayu, “Analisis Algoritma Klasifikasi Neural Network Untuk

Diagnosis Penyakit Kanker Payudara,” Jurnal Pilar Nusa Mandiri, vol. 15, no. 2, pp. 149–156, Aug. 2019, doi: 10.33480/pilar.v15i2.601.

• [3]    C. Song, S. Sugiharto, and O. D. Wahyuni, “Edukasi Kanker Payudara Dan Deteksi Dinipada

Kader Wanita Kelurahan Tomang,” Jurnal Bakti Masyarakat Indonesia, vol. 4, no. 2, pp. 351– 359, Aug. 2021.

• [4]    E. Susilowati, A. T. Hapsari, M. Efendi, and P. E. Kresnha, “Diagnosa Penyakit Kanker

Payudaramenggunakan Metode K-Means Clustering,” JUST IT: Jurnal Sistem Informasi, Teknologi Informasi dan Komputer, vol. 10, no. 1, pp. 27–32, 2019, [Online]. Available: https://jurnal.umj.ac.id/index.php/just-it

• [5]    H. Wijaya, “Optimization of Application of Genetic Algorithm Using C4.5 Method to Predict

Breast Cancer Disease,” bit-Tech, vol. 2, no. 1, pp. 1–9, 2019, [Online]. Available:

http://jurnal.kdi.or.id/index.php/bt

• [6]    C. Aroef, Y. Rivan, and Z. Rustam, “Comparing random forest and support vector machines for

breast cancer classification,” Telkomnika (Telecommunication Computing Electronics and Control), vol. 18, no. 2, pp. 815–821, Apr. 2020, doi: 10.12928/TELKOMNIKA.V18I2.14785.

• [7]    H. Oktavianto and R. P. Handri, “Analisis Klasifikasi Kanker Payudara Menggunakan Algoritma

Naive Bayes,” Informatics Journal, vol. 8, no. 2, pp. 45–54, 2019, [Online]. Available:

https://archive.ics.uci.edu/ml/.

• [8]     D.       Gustiar,       S.       H.       Sitorus,       and       D.       M.       Midyanti,

“Penerjemahan Bahasa Isyarat Menggunakan Metode Generalized Learning Vector Quantization (GLVQ)” Coding: Jurnal Komputer dan Aplikasi, vol. 8, no. 03, pp. 1-8, 2020.

• [9]    C. Diao, D. Kleyko, J. M. Rabaey, and B. A. Olshausen, “Generalized Learning Vector

Quantization for Classification in Randomized Neural Networks and Hyperdimensional Computing,” in 2021 International Joint Conference on Neural Networks (IJCNN), Jun. 2021, pp. 1–9. doi: 10.1109/IJCNN52387.2021.9533316.

• [10]    T. Villmann, A. Bohnsack, and M. Kaden, “Can learning vector quantization be an alternative to SVM and deep learning? - Recent trends and advanced variants of learning vector quantization for classification learning,” Journal of Artificial Intelligence and Soft Computing Research, vol. 7, no. 1, pp. 65–81, 2017, doi: 10.1515/jaiscr-2017-0005.

• [11]    R. Arniantya, B. D. Setiawan, and P. P. Adikara, “Optimasi Vektor Bobot Pada Learning Vector Quantization Menggunakan Algoritme Genetika Untuk Identifikasi Jenis Attention Deficit Hyperactivity Disorder Pada Anak,” Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer, vol. 2, no. 2, pp. 679–687, Feb. 2018, [Online]. Available: http://j-ptiik.ub.ac.id

• [12]    W. A. Setyowati and W. F. Mahmudy, “Optimasi Vektor Bobot Pada Learning Vector Quantization Menggunakan Particle Swarm Optimization Untuk Klasifikasi Jenis Attention Deficit Hyperactivity Disorder (ADHD) Pada Anak Usia Dini,” Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer, vol. 2, no. 11, pp. 4428–4437, Nov. 2018.

• [13]    I. Romadhona, I. Cholissodin, and Marji, “Penerapan Algoritme Particle Swarm OptimizationLearning Vector Quantization(PSO-LVQ) Pada Klasifikasi Data Iris,” Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer, vol. 2, no. 12, pp. 6418–6428, 2018, [Online]. Available: http://j-ptiik.ub.ac.id

• [14]    K. D. Prebiana, I. G. S. Astawa, and I. W. Supriana, “Optimasi Pembobotan Jaringan Syaraf Tiruan Pada Klasifikasi Kanker Payudara,” Jurnal Elektronik Ilmu Komputer Udayana, vol. 9, no. 1, pp. 151–159, Aug. 2020.

• [15]    E. Purwaningsih, “Penerapan Particle Swarm Optimization pada Metode Neural Network untuk Perawatan Penyakit Kutilmelalui Immunotherapy,” JUSTIN: Jurnal Sistem dan Teknologi Informasi, vol. 8, no. 2, pp. 207–211, 2020, doi: 10.26418/justin.v8i2.39869.

• [16]    Henderi, T. Wahyuningsih, and E. Rahwanto, “Comparison of Min-Max normalization and Z-Score Normalization in the K-nearest neighbor (kNN) Algorithm to Test the Accuracy of Types of Breast Cancer,” International Journal of Informatics and Information System, vol. 4, no. 1, pp. 13–20, Mar. 2021, [Online]. Available: http://archive.ics.uci.edu/ml.

• [17]    C. Leys, M. Delacre, Y. L. Mora, D. Lakens, and C. Ley, “How to classify, detect, and manage univariate and multivariate outliers, with emphasis on pre-registration,” International Review of Social Psychology, vol. 32, no. 1, pp. 1–10, 2019, doi: 10.5334/irsp.289.

Bimantara, dkk.

Klasifikasi Kanker Payudara Menggunakan Generalized Learning Vector Quantization (GLVQ) dan Particle Swarm Optimization (PSO)

• [18]   Suyanto, Data Mining Untuk Klasifikasi dan Klasterisasi Data, Revisi. Bandung: Informatika

Bandung, 2018.

• [19]   M. S. N. van Delsen, A. Z. Wattimena, and S. D. Saputri, “Penggunaan Metode Analisis

Komponen Utama Untuk Mereduksi Faktor-Faktor Inflasi Di Kota Ambon,” Jurnal Ilmu Matematika dan Terapan, vol. 11, no. 2, pp. 109–118, Dec. 2017, Accessed: Mar. 05, 2022. [Online]. Available: https://ojs3.unpatti.ac.id/index.php/barekeng/article/view/352

• [20]    Suyanto, Swarm Intelligence Komputasi Modern Untuk Optimasi dan Big Data Mining. Bandung: Informatika Bandung, 2017.

• [21]    S. Ramzini, D. E. Ratnawati, and S. Anam, “Penerapan Metode Learning Vector Quantization (LVQ) untuk Klasifikasi Fungsi Senyawa Aktif Menggunakan Notasi Simplified Molecular Input Line System (SMILES),” Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer, vol. 2, no. 12, pp. 6160–6168, Dec. 2018, [Online]. Available: http://j-ptiik.ub.ac.id

• [22]    L. A. A. R. Putri and S. Hartati, “Klasifikasi Genre Musik Menggunakan Learning Vector Quantization dan Self Organizing Map,” Jurnal Ilmiah ILMU KOMPUTER Universitas Udayana, vol. 9, no. 1, pp. 14–22, Apr. 2016.

• [23]    M. D. Ariyawan, I. G. A. Wibawa, and L. A. A. R. Putri, “Diagnosis of Heart Disease Using Generalized Learning Vector Quantization (GLVQ) and Genetic Algorithms Methods,” Jurnal Ilmu Komputer, vol. 13, no. 1, pp. 56–64, 2020.

• [24]    S. Saralajew, L. Holdijk, M. Rees, and T. Villmann, “Robustness of Generalized Learning Vector Quantization Models against Adversarial Attacks,” in International Workshop on Self-Organizing Maps, Feb. 2019, pp. 189–199. doi: 10.1007/978-3-030-19642-4_19.

• [25]    D. Devarriya, C. Gulati, V. Mansharamani, A. Sakalle, and A. Bhardwaj, “Unbalanced breast cancer data classification using novel fitness functions in genetic programming,” Expert Systems with Applications, vol. 140, Feb. 2020, doi: 10.1016/j.eswa.2019.112866.

318