Sistem Perolehan Citra Piercing Berdasarkan Pendekatan Codebook Dan Keyblock
on
Jurnal Ilmu Komputer VOL. XII No. 2
p-ISSN: 1979-5661
e-ISSN: 2622-321X
Sistem Perolehan Citra Piercing
Berdasarkan Pendekatan Codebook Dan Keyblock
I Gusti Agung Gede Arya Kadyanan
Program Studi Teknik Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana
Bukit Jimbaran, Indonesia
Abstract
Makalah ini menyajikan pengembangan sistem perolehan citra piercing berdasarkan pendekatan codebook dengan fitur tekstur dengan keyblock. Di dalam upaya membangun suatu platform pengembangan sistem perolehan citra warisan budaya, diperlukan suatu pendekatan yang handal untuk membangun berbagai sistem perolehan citra seperti batik dan lukisan. Keyblock merupakan generalisasi sistem temu kembali berbasis konten pada domain citra. Codebook dibangun berdasarkan pengelompokan nilai keyblock yang mewakili karakteristik citra pada data yang digunakan. Untuk data eksperimen, digunakan 41 pola piercing asli dan divariasikan menjadi 9 orientasi dan skala sehingga menjadi berjumlah 369 citra, dengan rincian sejumlah 328 citra untuk training data dan 41 citra untuk testing data atau kueri. Hasil yang optimal dicapai pada penggunaan ukuran keyblock 2x2 dan ukuran codebook 300 dengan rata-rata distorsi sebesar 19.07 tingkat keabuan dan RMS_error rata-rata sebesar 6.65 tingkat keabuan. Tingkat keberhasilan sistem perolehan citra dinyatakan dengan grafik precision dan recall, dengan kurva terbaik dicapai pada penggunaan teknik matching berdasarkan vector space (SVM).
Keywords: keyblock, vektor quantization, codebook, Generalized Lloyd Algorithm, piercing
Sebuah citra dapat mewakili sejuta makna, suatu ungkapan yang sangat tepat untuk merepresentasikan kemampuan yang terkandung dalam sebuah citra. Pemanfaatan citra digital dalam berbagai aplikasi menunjukkan peningkatan yang tinggi. Pengguna dengan berbagai latar belakang dapat melakukan akses dan manipulasi citra yang tersimpan didalam berbagai server [1]. Sistem perolehan citra dari basis data yang berbasis konten tidak selalu memberikan hasil yang memuaskan. Hal ini diakibatkan karena kompleksitas informasi yang terkandung dalam suatu citra, terutama bila basis data citra tidak dibatasi oleh suatu ranah aplikasi tertentu. Sistem perolehan citra berbasis konten menjadi sebuah area penelitian yang sangat penting saat ini, terutama karena adanya tuntutan efektivitas dan akurasi. Studi tentang sistem perolehan citra warisan budaya sebelumnya dilakukan dengan ranah aplikasi citra batik dan studi yang akan datang mungkin akan dilakukan dengan data lukisan. Makalah ini menjelaskan tentang penggunaan platform pengembangan sistem perolehan citra berdasarkan keyblock untuk citra piercing.
Terinspirasi dengan sistem temu kembali informasi berbasis teks, pengusul konsep keyblock [5] mencoba untuk menggunakan teori-teori yang dipakai pada temu kembali teks ke dalam domain citra dengan menempatkan codebook sebagai dictionary dan keyblock sebagai keyword-nya. Pendekatan keyblock pertama kali diajukan untuk sistem temu kembali citra oleh L. Zhu dkk. pada tahun 2002[5]. Keyblock mendekomposisi ulang setiap citra menjadi blok yang sama besar lalu menggunakan vektor quantization (VQ) untuk mencari blok-blok kunci untuk membentuk codebook yang mewakili setiap blok di seluruh citra pada basis data. Gambar 1, menunjukkan diagram alir kerja keyblock.

Gambar 1. Diagram alir untuk ekstraksi fitur berdasarkan keyblock (dimodifikasi dari [5]).
Langkah pertama, berdasarkan ukuran blok yang ditentukan, setiap citra di dekomposisi ulang menjadi sejumlah blok kecil yang berisi fitur dari sub area bersangkutan. Berdasarkan blok-blok tersebut dari contoh citra di basis data, sebuah codebook yang berisi keyblock dibangun dengan algoritma pengklusteran VQ (Vektor Quantizer) seperti GLA (Generalized Lloyd Algorithm) atau PNNA (Pairwise Nearest Neighbor Algorithm). Langkah kedua, setiap citra di basis data diencoding dengan menggunakan codebook yang berhasil dibentuk. Dimulai dengan mendekomposisi ulang citra menjadi blok-blok dengan besaran yang sama dengan saat pembentukan codebook diatas. Untuk setiap blok, dicari entri terdekat pada codebook untuk disimpan indeksnya. Dengan cara tersebut, setiap citra dapat di representasikan sebagai sebuah vektor nilai fitur yang setiap nilainya terhubung dengan indeks keyblock pada codebook. Berikut pada gambar 2 adalah skema untuk proses encoding dan decoding:

Gambar 2. Procedure untuk proses encoding dan decoding (dimodifikasi dari [7]).
Langkah terakhir, semua citra di basis data disimpan dalam bentuk vektor nilai fitur tersebut. Rekonstruksi citra dilakukan dengan mengacu kembali ke codebook dan hasil rekonstruksi merupakan pendekatan dari citra aslinya. Dengan menggunakan indeks dari keyblock, maka citra menjadi sama dengan dokumen teks yang memiliki struktur 1- dimensi linier. Oleh karenanya, generalisasi sistem temu kembali teks berdasarkan keyword dapat digunakan di domain citra berdasarkan keyblock [6].
-
2.2. Generalized Lloyd Algorithm (GLA)
GLA adalah algoritma pengklusteran berulang yang memperkirakan kondisi optimal selama perulangan berlangsung saat mendesain vektor kuantisasi. Pada setiap perulangan, langkah pertama, himpunan vektor pelatihan dibagi menjadi beberapa kluster berdasarkan kondisi tetangga terdekat menurut codebook yang telah dibentuk saat perulangan sebelumnya, adapun codebook awalnya ditentukan secara random. Langkah kedua, centroid setiap sel di hitung dan menggantikan vektor codebook sehingga codebook berisi seluruh centroid pada tahap tersebut. Langkah ketiga, keseluruhan distorsi dihitung dan perubahan distorsi diuji. Jika
perubahan distorsi melebihi suatu nilai threshold, maka proses-proses diatas perlu diulang, jika sebaliknya maka perulangan dihentikan [7].
Adapun langkah-langkah didalam algoritma GLA dapat dijelaskan sebagai berikut [8]:
-
• Langkah 1 (inisialisasi):
-
- Pilih training set T = {t1, ..., tl} secara random;
-
- Tentukan suatu nilai threshold δ;
-
- Tentukan codebook awal, Cl = {c1, ..., ci, ..., cN} secara random;
-
- Rata-rata distorsi awal, D0 = ∞ (suatu nilai yang besar); dan
-
- Tentukan jumlah iterasi, m = 1.
-
• Langkah 2 (iterasi pengklusteran)
Untuk i= 1,2, ..., l, untuk j=1,2, ..., N, hitung d t, cJ dan kemudian berdasarkan ciri
tetangga terdekat, hitung
Pk = {ti ∈ T I k = arg min d(ti, cj)},
…...…………………………………………………………………(1) untuk mencari klaster baru dari T dengan distorsi minimal
P = {Pι,∙∙∙, Pi ,∙∙∙, Pn }
-
• Langkah 3 (perhitungan distorsi)
Hitung rata-rata distorsi pada himpunan pelatihan terhadap codebook saat ini C .
Dm = 1 VNy d (t, cj)
-
m I Zm=1Z-M ∈ Pi ,
…………………….………………………………………………………..……….(2)
Dm I— Dm
jika — m ≤ δ , maka iterasi selesai dan C sebagai codebook akhir, bila tidak
Dm m
terpenuhi maka iterasi dilanjutkan.
Langkah 4 (perbarui codebook)
Buatlah codebook Cm+1 yang baru dengan menghitung centroid dari setiap partisi P;
ci
= π∑ t IP ∑t ∈ P
(3)
dan ganti codebook Cmyang lama dengan codebook Cm+1, yang baru, perbarui m = m +1
dan lanjutkan ke langkah 2.
-
2.3 . Root Mean Square error (RMS_error)
Untuk melihat kualitas codebook yang dihasilkan, maka dilakukan proses decoding, yaitu merekonstruksi seluruh citra pelatihan hasil proses encoding. Selanjutnya, dihitung RMS_error intensitas keabuan antara citra asli dan citra hasil rekonstruksi dengan rumus berikut ini.
1 N1 -1N 2-1
MSE = IF7Γ∑Σ (x [ n1, n 2] - x[ n1, n 2])2.....................................................................(4)
N1N2 n1=0n2=0
Dimana,
N : ukuran baris
N : ukuran kolom
-
n : koordinat baris
-
n : koordinat kolom
-
x : nilai keabuan piksel citra asli
-
xˆ : nilai keabuan piksel citra rekonstruksi
Dalam penelitian ini, hasil pengukuran distorsi juga merupakan suatu faktor pertimbangan penting dalam optimasi pembentukan codebook. Dalam proses ini akan dihitung jarak Euclidean dari tiap vektor pada citra piercing yang asli dengan keyblock yang terkait. Rumus penghitungan distorsi dapat dilihat pada Persamaan (2) yaitu pada pembahasan Generalized Lloyd Algorithm (GLA). Hasil perhitungan distorsi untuk semua ukuran blok dan jumlah codebook dapat dilihat pada Tabel 1.
-
2.5 Precision dan Recall
Efektifitas sebuah sistem perolehan citra berbasis konten biasanya diekspresikan dengan istilah precision dan recall. Berdasarkan teori perolehan informasi, precision didefinisikan sebagai jumlah dokumen relevan yang diperoleh hasil suatu kueri dibagi seluruh dokumen yang diperoleh, sedangkan recall didefinisikan sebagai jumlah dokumen yang relevan yang diperoleh hasil suatu kueri dibagi dengan total dokumen relevan yang ada. Untuk lebih tepatnya, asumsikan himpunan yang diperoleh sebagai himpunan citra yang diperoleh sebagai jawaban suatu kueri, dan himpunan yang relevan sebagai himpunan citra pada basis data yang telah ditentukan sebagai jawaban relevan bagi suatu kueri, maka rumusnya adalah:
I himpunan yang diperoleh ∩ himpunan yang relevan | precision=----------—---------------—-----------
(5)
(6)
I himpunan yang diperoleh |
I himpunan yang diperoleh ∩ himpunanyang relevan | recaLl =----------rr-----------;—i----------
I himpunanyang relevan |
Model yang digunakan dalam perolehan citra piercing dengan teknik perolehan citra yaitu quintuple [D, K, W, Q, S] dimana:
-
• D = {d1,...,dj, —,dn} adalah daftar citra piercing terkompresi VQ, dan n disini merupakan jumlah citra piercing di basis data.
-
• K = {k1, —,ki, —,kt} adalah daftar keyblock pada codebook, dan t merupakan jumlah keyblock di codebook.
-
• W : K × D → R+ adalah pemetaan yang memetakan pasangan keyblock dan citra pada sebuah angka positif. Bila wi j= W(ki,djJ maka W direpresentasikan sebagai matrik (w. .t×n disebut bobot matrik yang tiap elemennya adalah indeks keyblock pada sebuah citra dimana t adalah jumlah keyblock di codebook dan n adalah jumlah citra di basis data . Setiap citra dj, memiliki sejumlah vektor ciri dj = {w1 j^., wt j}.
-
• Q = {qι,—qc,.,Qi} adalah himpunan citra kueri. Setiap citra kueri memiliki ciri vektor q = {Wi ,.-w Wt} yang sama dengan vektor ciri dj.
-
• S : Q x D ÷ R+ ukuran kesamaan antara kueri dan citra. Nilai ini digunakan untuk membuat rangking citra yang diperoleh.
Tiga ukuran kesamaan yang dipakai pada sistem perolehan citra piercing pada penelitian ini yaitu: berdasarkan kesamaan cosine (SCOS), histogram (SHM), dan vektor space (SVM).
-
2.7 Kesamaan Cosine (SCOS)

Gambar 3. Kesamaan Cosine (SCOS).
Kesamaan cosine (SCOS) adalah pengukuran kesamaan antara dua vektor dengan mencari nilai cosine (SCOS) dari sudut antara kedua vektor tersebut [9]. Pada perolehan citra, kesamaan cosine (SCOS) antar dua citra berkisar antara 0 – 1 dan sudut antara kedua vector tidak lebih dari 90o. Pada dua buah vektor d dan q, dimana ddanq merupakan frekuensi kemunculan setiap keyblock, maka kesamaan cosine (SCOS)-nya adalah:
d,- q ∑',w. *
……………………………………………………….(7)
wi,q
S cos [q, d j]= cos φ = J = ∑
; i=1 w 2 ij *
-
2.8 Model Vektor Space (SVM).
Metode perolehan informasi berbasis vektor merepresentasikan dokumen dan kueri dengan suatu vektor, serta menghitung kesamaannya dengan inner product yang dapat dilihat pada Persamaan (11). Dengan menormalisasi vektor menjadi satuan panjang, inner product mengukur kosinus sudut antara dua vektor pada ruang vektor [9].
Bila ada n citra piercing pada D dan t keyblock pada K, maka normalisasi kemunculan keyblock k pada citra d adalah:
tfi,j
ni,j
∑
……………………………….……………………………………………..…(8)
Dimana n adalah frekuensi kemunculan keyblock k pada citra d dan n adalah frekuensi i, j i j t,j
kemunculan seluruh keyblock pada citra d .
df adalah jumlah citra yang memiliki k . Inverse dari df adalah:
n
Idfi = log-----7 ....................................................................................................(9)
1 + f
Sehingga w yaitu bobot keyblock i pada citra j dapat dihitung dengan:
n
w,,j = f,Jidfi = f,j loS1----7 ...................................................................................(10)
1 + f
metode ini memberikan bobot besar pada keyblock yang sering muncul pada citra D. Bobot
untuk kueri q yaitu w , dihitung serupa. Metode vektor space menghitung kesamaan dengan i,q
inner product antara dua vektor:
SVM {fl’ dJ ] =
dj.. q
t
i=ι w i ■ j wi ■ q
IdIq ∑. ■■ ∙,∑∑= ■■
(11)
Perolehan citra dengan model ini menggunakan histogram dari frekuensi kemunculan seluruh keyblock pada suatu citra[14] yang dalam penelitian ini citra yang dimaksud adalah citra piercing, dimana wij = ft yang artinya bobot keyblock i pada citra j sama dengan frekuensi k. muncul pada dj. Begitu juga dengan wiq = fi Nilai kesamaan dihitung dengan :
SHM (q, dj )= _ - ........................
(12)
(13)
1 + dis (q, d j )
Dimana fungsi distance atau jarak dihitung dengan:
dis (q, d j )= ∑ t==1
I wi, j — wi, q\
1 + wi, j + wi, q
Dari 328 citra piercing yang digunakan untuk training data, dan sejumlah 41 citra piercing untuk citra kueri, secara keseluruhan memiliki dimensi citra yang sama yaitu 128 x 96. Dari hasil eksperimen ternyata blok citra dengan ukuran 2x2 yang menghasilkan akurasi yang terbaik dengan beberapa variasi jumlah codebook yaitu diantaranya 100, 200, 300, 400, dan 500. Pada Gambar 3 dibawah ini dapat dilihat representasi sejumlah 41 citra yang diambil secara random untuk kueri.
|
Wj |
⅜ |
Wl |
⅛ | ||
|
Wi |
≠ I |
W |
<S |
⅛ |
W |
|
^ |
⅛ |
w |
® |
<⅛> | |
|
® |
^J |
% |
® |
*1 | |
|
e |
‘^ |
⅜ |
⅛ |
^ | |
|
^ |
⅛β i |
⅛ |
(P | ||
|
* |
JLl |
Jj |
o I |
Gambar 4. Sejumlah 41 citra piercing untuk kueri yang dipilih secara random dari 369 data.
Pada Gambar 5, dapat dilihat citra piercing hasil rekonstruksi dari ukuran blok 2x2 dengan jumlah codebook yang hanya ditampilkan diantaranya 100, 300, dan 500. Dari hasil eksperimen ini menunjukkan bahwa codebook dapat digunakan sebagai vector quantifier untuk proses encoding dan decoding citra piercing. Selanjutnya, kualitas citra hasil rekonstruksi diuji dengan rata-rata RMS_error terhadap citra aslinya. Dari hasil citra rekonstruksi pada Gambar 5 diperoleh nilai rata-rata RMS error yang dihitung dengan Persamaan (4), yaitu masing-masing 9.42, 6.65, dan 6.57 (nilai rata-rata RMS error dari seluruh blok dan codebook dapat dilihat pada Tabel 2). Berikut adalah representasi citra rekonstruksi dari blok 2x2 dengan codebook 100:

Gambar 5. Citra rekonstruksi dengan blok 2 x 2 dan codebook 100.
|
⅛ |
W | |||
|
W |
φ |
⅛ | ||
|
W |
1# |
® | ||
|
Φ |
¾ | |||
|
S | ||||
|
^ |
0> |
«5 |
Histogram sebuah citra piercing merupakan representasi grafis dari frekuensi intensitas piksel yang ada pada citra tersebut. Pada sebuah citra keabuan 8 bit, nilai keabuan mencapai 256, sedangkan pada citra dengan 16 bit, nilai keabuan mencapai 65.536. Gambar 6 dan Gambar 7 berikut menunjukan tipikal histogram untuk citra asli dan citra rekonstruksi dari citra pertama:
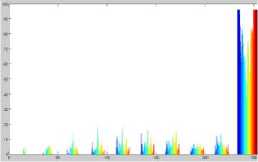
Gambar 6. Histogram citra piercing asli pertama.

Gambar 7. Histogram rekonstruksi citra pertama.
Kedua histogram memiliki 10 peak dan setiap peak dipisahkan antara 5 – 15 tingkat intensitas keabuan. Dengan jarak antar peak yang mencapai 15 tingkat intensitas keabuan, ternyata nilai RMS_error yang hanya mencapai 9 tingkat tidak akan mengakibatkan perpindahan peak pada tiap piksel yang mengakibatkan perubahan citra yang signifikan.
Tabel 2. Rata-rata RMS_error pada setiap ukuran codebook dan blok
|
Ukuran blok |
Uk | |
|
100 |
200 | |
|
2 x 2 |
9.42 |
7.52 |
|
4 x 4 |
15.83 |
14.84 |
|
8 x 8 |
23.58 |
21.20 |
|
uran codebook | ||
|
300 |
400 |
500 |
|
6.65 |
6.92 |
6.57 |
|
14.20 |
14.48 |
13.23 |
|
20.44 |
20.23 |
19.77 |
Tabel 1. Rata-rata distorsi pada setiap ukuran codebook dan blok
|
Ukuran blok |
Ukuran codebook | ||||
|
100 |
200 |
300 |
400 |
500 | |
|
2 x 2 |
30.22 |
22.24 |
19.07 |
21.19 |
23.02 |
|
4 x 4 |
102.08 |
94.42 |
80.85 |
90.77 |
84.33 |
|
8 x 8 |
307.34 |
259.57 |
239.78 |
232.73 |
239.72 |
Pada Tabel 2 diatas menunjukan nilai rata-rata RMS_error untuk seluruh citra piercing pada setiap ukuran codebook dan keyblock yang dibentuk. Dari Tabel 2 terlihat bahwa untuk satu ukuran codebook, semakin kecil ukuran keyblock, semakin kecil rata-rata RMS_error yang terjadi. Kinerja perolehan cenderung menurun dengan membesarnya ukuran blok. Grafik Precission dan Recall dapat dilihat pada gambar 8 dibawah ini:

Gambar 8. Grafik Precission dan Recall dengan blok 2 x 2 dan codebook 100.
Gambar 9 menunjukan bahwa teknik perolehan kesamaan vector space(SVM) memiliki kinerja paling baik diantara ketiga teknik perolehan lainnya untuk semua ukuran blok dan codebook yang dicobakan, hal ini dapat dilihat pada ketiga grafik Precission dan Recall diatas.

Gambar 9. Representasi codebook dengan blok 2 x 2 dan jumlah codebook 100.
Hasil studi ini memberikan kesimpulan sebagai berikut:
-
1) Ciri tekstur citra piercing dapat diekstraksi dengan pendekatan codebook dan keyblok. Berdasarkan keberhasilan didalam sistem temu kembali berbasis text, dengan ini sistem temu kembali informasi berdasarkan konten pada domain citra piercing dapat dilakukan dengan merepresentasi citra piercing diubah menjadi vektor ciri 1-dimensi dengan
melakukan encoding berdasarkan codebook yang telah dibentuk.
-
2) Akurasi terbaik diperoleh pada ukuran blok 2x2 dan codebook 300, dengan melihat tampilan citra piercing hasil rekonstruksi secara visual dan diperkuat dengan menghitung nilai rata-rata RMS_error dapat disimpulkan bahwa kerusakan citra piercing ketika rekonstruksi tidak terlalu signifikan karena nilai rata-rata distorsi 19.07 tingkat keabuan dan nilai rata-rata RMS_error yaitu 6.65 tingkat keabuan pada blok 2x2 masih dianggap dalam batas toleransi.
Model kesamaan Vektor Space (SVM) menunjukan kinerja yang terbaik dibandingkan dengan dua model perolehan lainnya, hal ini dapat dilihat pada ketiga grafik Precission dan Recall pada gambar 8.
References
-
[1] J. Eakins dan M. Graham, “Content-based Image Retrieval,” Technology Applications Programme Report 39, University of Northumbria at Newcastle, October 1999.
-
[2] http://en.wikipedia.org/wiki/CBIR, Content-based image retrieval” [accessed in October 1, 2009].
-
[3] R. M. Haralick, K. Shanmugam, dan I. Dinstein, “Textural Feature for Image Classification,” IEEE Transactions on Sistem, Man dan Cybernetics, Vol SMC-3 No. 6, November 1973.
-
[4] P. Brodatz, “Textures”, New York, Dover, 1966.
-
[5] L. Zhu dan A. Zhang, “Theory of Keyblock-based Image Retrieval,” ACM Journal, pp. 1-32, March 2002.
-
[6] L. Zhu, A. Rao, dan A. Zhang, “Advanced Feature Extraction for Keyblok-based Image Retrieval,” Proceedings of International Workshop on Multimedia Information Retrieval (MIR 2000), Los Angeles, California, USA, November 4, 2000.
-
[7] L. Zhu, A. Rao, dan A. Zhang, 2000, “Keyblok: An approach for content-based geographic image retrieval,” Proceedings of First International Conference on Geographic Information Science (GIScience2000), Savannah, Georgia, USA, 286–287, 2000.
-
[8] L. Zhu, C. Tang, dan A. Zhang, “Using Key blok Statistics to Model Image Retrieval,” Advances in Multimedia Information Processing – PCM 2001, Second IEEE Pacific Rim Conference on Multimedia, Beijing, China, October 24-26, 2001, Proceedings 2001.
-
[9] Yates, R.B, dan B.R. Neto. Modern Information Retrieval. Addison Wesley, 1999.
91
Discussion and feedback