Implementasi Support Vector Regression Untuk Prediksi Harga Rumah Dengan Optimasi Grid Search

Jurnal Elektronik Ilmu Komputer Udayana

Volume 12, No 3. Februari 2024

p-ISSN: 2301-5373

e-ISSN: 2654-5101

Implementasi Support Vector Regression untuk Prediksi Harga Rumah Dengan Optimasi Grid Search

Mulyawan^a1, Reza Subagja^b2, Dede Rohman^b3, Deny Indriyana Efendi^b4

^aProgram Studi Sistem Informasi, STMIK IKMI Cirebon

Jl. Perjuangan No.10B, Karyamulya, Kec. Kesambi, Kota Cirebon, Jawa Barat 45135 ¹mulyawan@gmail.com

^bProgram Studi Teknik Informatika, STMIK IKMI Cirebon

Jl. Perjuangan No.10B, Karyamulya, Kec. Kesambi, Kota Cirebon, Jawa Barat 45135 ²rezasubagja5@gmail.com ³dederohman@gmail.com

⁴dendyindriyaefendi@gmail.com

Abstract

Rumah merupakan kebutuhan pokok dalam kehidupan manusia, berfungsi sebagai tempat perlindungan tidak hanya dari kondisi cuaca eksternal, tetapi juga dari makhluk hidup lainnya. Harga rumah menjadi elemen kunci dalam transaksi properti, baik melalui cara konvensional maupun digital. Penelitian ini memiliki tujuan untuk menerapkan algoritma Support Vector Regression (SVR) dalam konteks prediksi harga rumah berdasarkan karakteristiknya. Dalam upaya mencapai kinerja model yang optimal, dilakukan optimasi parameter menggunakan algoritma Grid Search. Data yang digunakan diperoleh melalui teknik web scraping dari situs properti rumah123.com, dengan fokus pada wilayah Jakarta. Atribut data mencakup lokasi, luas tanah, luas bangunan, jumlah kamar tidur, jumlah kamar mandi, kapasitas garasi, dan harga rumah. Metode penelitian melibatkan langkah-langkah Obtain, Scrub, Explore, Model, dan Interpret. Dalam pemodelan, dua skenario data dieksplorasi, yakni menggunakan dataset asli dan hasil transformasi logaritma pada variabel target. Hasil penelitian menunjukkan bahwa model terbaik ditemukan pada skenario data hasil transformasi logaritma, dengan nilai metrik RMSE = 0.2774, MAE = 0.2061, MAPE = 0.1453, dan R-Squared = 0.7867. Parameter optimal yang dihasilkan dari metode grid search adalah Cost = 1, epsilon = 0.1, dan gamma = 1.

Keywords: Prediksi Harga Rumah, Support Vector Regression, Grid Search

• 1.    Pendahuluan

Rumah merupakan salah satu kebutuhan dasar manusia, bersama dengan kebutuhan sandang dan pangan. Menurut Mulder (2006), seiring dengan pertumbuhan populasi, permintaan akan perumahan akan terus meningkat. Selain itu, perkembangan teknologi informasi telah membawa perubahan besar dalam industri properti. Banyak platform jual beli properti online bermunculan, menyediakan layanan bagi pengguna untuk saling bertransaksi secara efisien. Dalam konteks ini, data penjualan rumah yang terakumulasi di platform tersebut menjadi sangat kaya dan berpotensi untuk dieksplorasi. Perkembangan pesat tersebut menghadirkan tantangan dan peluang dalam peningkatan kualitas pengalaman pengguna. Berdasarkan survei peneliti, mayoritas platform jual beli rumah online saat ini belum memiliki fitur yang dapat melakukan prediksi harga rumah berdasarkan karakteristiknya. Kehadiran fitur prediksi harga rumah dapat mengatasi ketidakpastian dan meningkatkan transparansi di pasar properti digital. Salah satu teknologi yang mampu menyikapi masalah tersebut adalah machine learning. Machine learning adalah salah satu cabang dari kecerdasan buatan yang memungkinkan sistem komputer untuk belajar dari data, mengidentifikasi pola, dan membuat keputusan dengan sedikit atau tanpa campur tangan manusia secara eksplisit. Konsep utama di balik machine learning adalah memberikan kemampuan pada sistem untuk meningkatkan kinerjanya seiring waktu berdasarkan

pengalaman dan data yang telah diterima. Di samping itu, masalah yang kerap dihadapi para pengembang machine learning yaitu kesulitan dalam mengoptimasi parameter model. Optimasi parameter dilakukan untuk bisa meningkatkan kinerja dari model yang dihasilkan. Salah satu metode yang umum dilakukan yaitu dengan memanfaatkan algoritma grid search. Penelitian terdahulu telah menunjukkan bahwa machine learning dapat signifikan meningkatkan akurasi prediksi. Penelitian [1] menyatakan bahwa dalam penentuan harga rumah, terdapat 5 variabel yang dapat berpengaruh. Berdasar survei yang dilakukannya kepada para pengembang (developer) rumah, variabel bebas terdiri dari luas lahan, luas bangunan, banyaknya kamar tidur, banyaknya kamar mandi, hingga ketersediaan tempat parkir mobil. Selain variabel tersebut, lokasi rumah juga ikut berperan dalam penentuan harga [2]. Pada penelitian [3] menyatakan bahwa konsep algoritma support vector regression (SVR) dapat menghasilkan nilai peramalan yang bagus karena SVR mempunyai kemampuan menyelesaikan overfitting. Selain itu, penelitian [4] menunjukan bahwa algoritma grid search mampu mengatasi kesulitan dalam menentukan parameter optimal dalam proses pengembangan model support vector regression (SVR). Oleh karena itu, dengan mengintegrasikan temuan penelitian sebelumnya, penelitian ini bertujuan menghasilkan model support vector regression (SVR) terbaik untuk prediksi harga rumah dengan optimasi algoritma grid search. Langkah ini berdasarkan pada hasil penelitian sebelumnya yang telah membuktikan efektivitas SVR dan grid search dalam memodelkan hubungan kompleks antara variabel bebas dan variabel target.

• 2.    Metode Penelitian

Penelitian ini dilakukan berdasarkan tahapan metodologi OSEMN, dengan alat analisis data menggunakan google colaboratory versi python 3.10.12. Berikut adalah diagram alir dari tahapan penelititan:

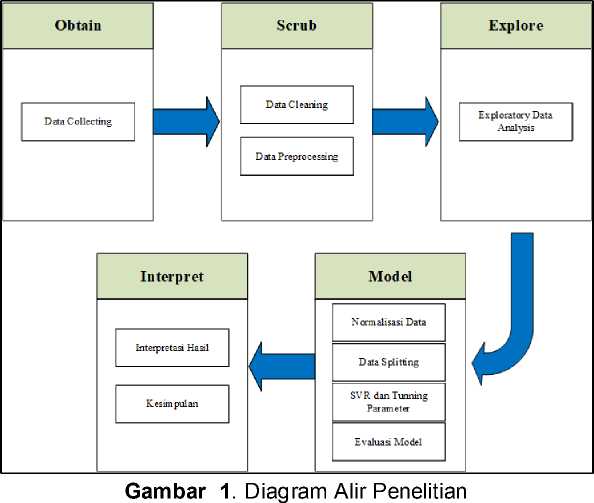
Teknik analisis data merupakan tahapan kritis dalam proses penelitian. Tujuan analisis data di sini adalah untuk mengidentifikasi pola umum dari data yang terkumpul melalui proses pengolahan atau penjelasan data tersebut [5]. Berikut teknik analisis data yang akan dilakukan dalam penelitian ini:

• 2.1.    Support Vector Regression

Support Vector Regression (SVR) merupakan teknik analisis data utama yang digunakan dalam penelitian ini. SVR adalah metode regresi yang berdasarkan konsep Support Vector Machines (SVM). SVM dirancang dan dikembangkan oleh Boser, Guyon, dan Vapnik, serta pertama kali diperkenalkan dalam Annual Workshop on Computational Learning Theory pada tahun 1992 [6].

SVM mampu mengatasi pemetaan data nonlinier dengan mengubah data uji asli ke dimensi yang lebih tinggi menggunakan fungsi kernel. Tujuan dari SVR adalah untuk mengidentifikasi suatu fungsi yang dapat direpresentasikan sebagai hyperplane atau garis pemisah dalam format fungsi regresi. Fungsi ini dimaksudkan untuk sesuai dengan seluruh data input dengan tingkat kesalahan yang minimal, sehingga membuat kesalahan tersebut sekecil mungkin [3]. Misalkan terdapat l data training, (xi,yi), i =1,…,l dengan data input x = {x_(1.)...,xj} ⊆ ¾N dan y = {y_1,. ,y_l} ⊆ ¾ dan l adalah banyaknya data training. Fungsi regresi dari metode SVR adalah sebagai berikut:

f(x)= w φ(x)+b

(1) [3]

Keterangan :

W         : Vektor pembobot

φ(x)         :  Fungsi yang memetakan x dalam suatu dimensi

b               :  Bias

• 2.2.    Algoritma Grid Search

Algoritma Grid Search adalah salah satu teknik pencarian parameter yang umum digunakan dalam tahap optimasi parameter model Support Vector Regression (SVR). Tujuannya adalah untuk menemukan parameter terbaik dalam dataset pelatihan agar model dapat dengan tepat memprediksi data uji [7]. Pada penerapannya, algoritma ini harus dipandu oleh beberapa metrik kinerja, dan biasanya diukur dengan cross-validation pada data latih [8]. Cross validation merupakan teknik evaluasi model yang membantu metode grid search dalam mengevaluasi kinerja model yang dihasilkan dari setiap kombinasi parameter. Proses kerja cross validation adalah dengan cara membagi dataset menjadi beberapa subset, yang disebut lipatan atau folds. Kemudian, model dilatih pada beberapa subset dan diuji pada subset yang tidak terlibat pelatihan. Proses ini berulang sampai hasil akhir dari cross validation berupa nilai rata-rata performa model yang konsisten. Pada penelitian ini dilakukan cross validation dengan jumlah folds sebanyak 5. Berikut pada gambar 2 merupakan ilustrasi dari proses metode grid search.

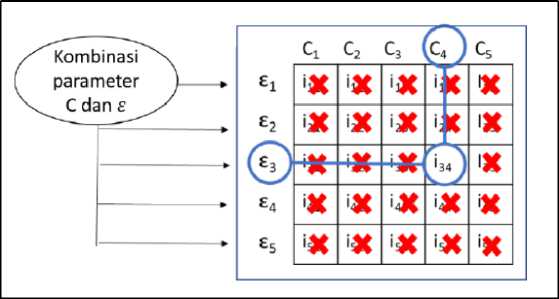
Gambar 2. Ilustrasi Algoritma Grid Search [4]

Pada penelitian ini, fungsi kernel yang dioptimasi yaitu kernel Gaussian Radial Basis Function (RBF). Hal ini didasarkan penelitian sebelumnya yang membuktikan bahwa kernel ini mampu menghasilkan kinerja model terbaik [9]. Pada SVR dengan kernel RBF, ada parameter lain yang harus dioptimasi yaitu C (cost), γ (gamma) dan ε (epsilon) [7]. Parameter cost berfungsi mengontrol trade-off antara presisi pemodelan data pelatihan dan kompleksitas model. Epsilon berperan menentukan batas kesalahan yang dapat diterima, sedangkan gamma mengontrol seberapa jauh pengaruh satu titik data terhadap titik data yang lain dalam sebuah model SVR. Fungsi kernel RBF dirumuskan dalam persamaan 2 berikut:

K(xi,xj) = exp (-—)(Xi — Xj)

( 2 ) [10]

2σ²

Keterangan Xi Xj σ 1 2σ2

Data ke – i Data ke – j Standart deviasi γ (gamma)

• 2.3.    Evaluasi Model

Teknik ini melibatkan penggunaan berbagai metrik evaluasi yang dirancang khusus untuk tipe masalah yang dihadapi. Dalam kasus regresi, ada banyak metrik yang bisa dijadikan alat evaluasi. Pada penelitian ini, proses evaluasi model menggunakan metrik Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), dan R-Squared.

Root Mean Square Error (RMSE) adalah metrik evaluasi yang mengukur seberapa besar perbedaan antara nilai prediksi yang dihasilkan oleh model dengan nilai aktual dalam skala yang sama. Untuk menghitung RMSE, langkah pertama dengan mengambil rata-rata dari kuadrat selisih antara nilai prediksi dan nilai aktual. Selanjutnya, nilai RMSE diperoleh dengan mengambil akar kuadrat dari rata-rata kuadrat selisih tersebut. RMSE memberikan gambaran tentang seberapa besar kesalahan prediksi secara keseluruhan, dengan nilai yang lebih kecil menunjukkan tingkat akurasi yang lebih tinggi. Secara matematis, rumus RMSE dijelaskan pada persamaan 3 berikut:

^rmse = √1∑ι^-^

( 3 )

Keterangan n

Yi

yi

Jumlah sampel dalam pengujian

Nilai aktual dari observasi ke-i

Nilai prediksi dari model untuk observasi ke-i

Mean Absolute Error (MAE) adalah metrik yang mengukur kesalahan prediksi suatu model dengan menghitung rata-rata dari nilai absolut selisih antara prediksi dan nilai sebenarnya. Semakin kecil nilai RMSE, semakin baik model dapat melakukan prediksi. Dalam konteks matematis, MAE untuk suatu model dapat dijelaskan sebagai persamaan 4 berikut.

MAE =

1 x—^{, n}

_i∑J^γi-^∣

( 4 )

Keterangan n

Yi

Yi

Jumlah sampel dalam pengujian

Nilai aktual dari observasi ke-i

Nilai prediksi dari model untuk observasi ke-i

Mean Absolute Percentage Error (MAPE) merupakan metrik evaluasi yang mengukur rata-rata dari persentase kesalahan absolut antara prediksi dan nilai sebenarnya. MAPE memberikan gambaran persentase kesalahan rata-rata antara prediksi dan nilai sebenarnya, dan seperti MAE, nilai yang lebih rendah menunjukkan kinerja model yang lebih baik. Pada bentuk matematisnya, rumus MAPE dijelaskan pada persamaan 5.

MAPE =

l^∙ .

Yi — Yi

—¹×¹⁰⁰

( 5 )

Keterangan

n            :  Jumlah sampel dalam pengujian

Yi             :  Nilai aktual dari observasi ke-i

Yi            :  Nilai prediksi dari model untuk observasi ke-i

R-squared (R²) sering disebut sebagai koefisien determinasi adalah metrik evaluasi yang memberikan indikasi tentang seberapa besar variabilitas dalam variabel target yang dapat dijelaskan oleh model. Secara umum, R-squared menyatakan proporsi variasi dalam variabel target yang dapat dijelaskan oleh variabel independen yang ada dalam model. Metrik ini memiliki nilai rentang dari 0 hingga 1, dimana nilai yang mendekati nilai 1 menunjukan bahwa kinerja model semakin baik. Rumus R-squared dapat dinyatakan dalam persamaan 6.

A²=I-

EUyi^-.^ ∑L₁(yi-j^i)²

( 6 )

Keterangan n

Yi

yi

yi

Jumlah sampel dalam pengujian

Nilai aktual dari observasi ke-i

Nilai prediksi dari model untuk observasi ke-i

Nilai rata-rata dari variabel target

• 3.   Hasil dan Pembahasan

Berikut merupakan hasil dari setiap tahapan metodologi penelitian:

• 3.1.  Obtain

Data diperoleh melalui proses scrapping dari website rumah123.com. Pemilihan data disesuaikan dengan format data penjualan rumah pada platform tersebut. Lingkup data dibatasi dengan wilayah Jakarta. Dataset yang dihasilkan terdiri dari atribut waktu_scrap, deskripsi, alamat, narahubung, luas_tanah_m2, luas_bangunan_m2, kamar_tidur, kamar_mandi, garasi, dan harga_miliar. Baris data yang berhasil dikumpulkan sebanyak 9.665 record. Data tersebut kemudian disimpan di penyimpanan berbasis cloud milik peneliti dengan format CSV agar mempermudah dalam proses analisis data selanjutnya.

• 3.2.    Scrub

Scrub melibatkan pembersihan dan pengolahan data awal pada dataset. Proses pembersihan memperhatikan faktor missing values, penyesuaian format, dan data outlier. Langkah-langkah tersebut diterapkan untuk menanggulangi ketidakpastian dan ketidakakuratan yang mungkin terjadi akibat proses scrapping data. Proses pembersihan data juga dapat berdampak signifikan pada kinerja sistem data mining, sebab penanganan data terkait akan mengalami pengurangan baik dalam hal jumlah maupun kompleksitas [11]. Metode Inter Quartile Range (IQR) diterapkan sebagai pendekatan dalam mendeteksi data outlier. Teknik ini dilakukan dengan cara mencari selisih antara kuartil ketiga dengan kuartil pertama [12]. Pada tahapan Scrub, dataset yang dihasilkan terdiri dari 7 kolom atribut. Informasi hasil pengolahan dataset dapat dilihat pada gambar 3.

<class ^,pandas.core.fname.DataFrame^,> Int64Index: 3990 entries, 5 to 9903 Data columns (total 7 columns):

# Column           Non-Null Count Dtype

0	Iokasi	399Θ non-null	int64
1	1 ua s_t a na h_m2	3990 non-null	float64
2	luas_bangunan_m2	3990 non-null	float64
3	kamar_tidur	3990 non-null	int64
4	kamarmandi	3990 non-null	int64
5	kapas itasgarasi	3990 non-null	int64
6	Iiargajniliar	3990 non-null	float64

dtypes: float64(3), int64(4)

memory usage: 249.4 KB

• Gambar 3. Dataset Hasil Tahap Scrub

Gambar 3 menjelaskan dataset hasil proses Scrub, memuat informasi total baris data, nama kolom, tipe data, dan informasi kelengkapan data pada tiap atribut. Hasil tersebut menjelaskan bahwa atribut yang dipakai yaitu lokasi, luas_tanah_m2, luas_bangunan_m2, kamar_tidur, kamar_mandi, kapasitas_garasi, dan harga_miliar. Total baris data yang digunakan ke tahap selanjutnya sebanyak 3.990 record.

• 3.3.    Explore

Tahapan Analisis eksploratif ini dilakukan untuk memahami pola-pola dan hubungan antarvariabel dalam dataset. Proses ini melibatkan statistika deksriptif, visualisasi distribusi data, dan perhitungan korelasi variabel menggunakan nilai korelasi Pearson [12]. Hasil proses Explore ditampilkan pada gambar berikut:

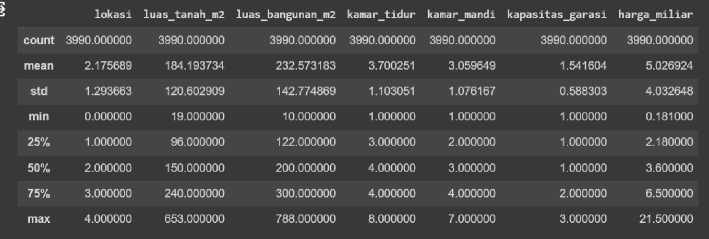
Gambar 4. Hasil Statistika Deskriptif

Gambar 4 tersebut menunjukan perhitungan statistika deskriptif dari setiap atribut. Statistika deskriptif bertujuan untuk mengetahui nilai-nilai khas atau karakteristik dari sekumpulan data. Nilai count merupakan banyaknya data pada tiap atribut kolom. Nilai mean adalah nilai rata-rata atribut dan std merupakan nilai simpangan baku. Untuk nilai 25%, 50%, dan 75% mewakili dari nilai kuantil satu sampai tiga dari setiap atribut. baris min dan max adalah kependekan dari nilai minimal dan maksimal dari setiap kumpulan data.

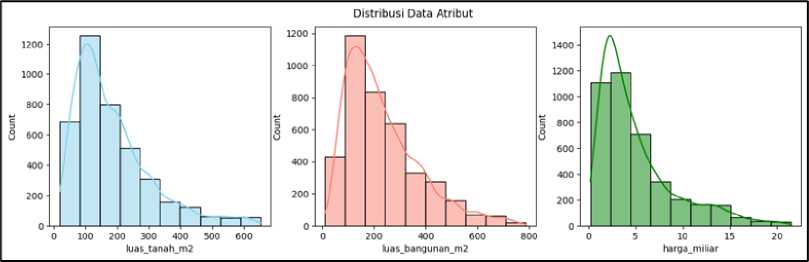
Gambar 5. Distribusi Data Atribut

Gambar 5 menunjukan distribusi data atribut luas_tanah_m2, luas_bangunan_m2, dan harga_miliar. Ketiga chart tersebut menunjukan bahwa kebanyakan data berkumpul pada nilai yang lebih rendah yang menyebabkan distribusi menjadi asimetris.

	lokasi	luas_tanah_m2	Iua s_ba n gu n a n_m 2	kamar_tidur	kamar_mandi	kapasitas_garasi	IiargajTiiliar
lokasi	1.000000	-0.119756	-0.118734	-0.053385	-0.024096	-0.019982	-0.252905
Iuas_tanah_m2	-0.119756	1.000000	0.675995	0.469173	0.361070	0.329136	0.744062
Iuasbangu nan_m2	-0.118734	0.675995	1.000000	0.527637	0.564736	0.351934	0.729006
kamar_tidur	-0.053385	0.469173	0.527637	1.000000	0.627710	0.266849	0.392201
kamar mandi	-0.024096	0.361070	0.564736	0.627710	1.000000	0.310474	0.411164
kapas itas_garasi	-0.019982	0.329136	0.351934	0.266849	0.310474	1.000000	0.330251
harga_miliar	-0.252905	0.744062	0.729006	0.392201	0.411164	0.330251	1.000000

Gambar 6. Nilai Korelasi Pearson

Gambar 6 tersebut menunjukan nilai korelasi atau hubungan antar atribut dataset. Dari hasil tersebut terlihat bahwa semua variabel kriteria memiliki korelasi positif dengan variabel target, kecuali atribut lokasi.

• 3.4.    Model

Langkah krusial dalam pelaksanaan Model adalah menggunakan data baru untuk menghasilkan perkiraan kasus yang relevan, sehingga dapat diuji keberlakuan model yang telah dibangun dalam memberikan solusi yang sesuai terhadap permasalahan yang dihadapi [13]. Berdasarkan chart distribusi data pada variabel luas_tanah_m2, luas_bangunan_m2, dan harga_miliar, terindikasi adanya distribusi data asimetris berjenis right-skewed. Distribusi data ini ditandai dengan berkumpulnya sebaran data pada nilai yang mendekati nilai nol. Distribusi data asimetris dapat mempengaruhi tingkat akurasi dalam proses pengembangan model. Dalam mengatasi hal tersebut, transformasi logaritma dapat dilakukan untuk mendekati distribusi normal [14]. Menurut Gujarati dan Porter (2009) dalam paper [15] menyebutkan salah satu model dengan transformasi variabel adalah model semilog, yaitu salah satu variabel muncul dalam bentuk logaritmik, atau dapat disebut model log-lin atau lin-log. Oleh karena itu, dua skenario pemodelan diterapkan, yaitu dengan data asli dan data hasil transformasi logaritma natural pada variabel target. Hal ini dilakukan untuk melihat perbedaan hasil evaluasi model dari kedua skenario tersebut.

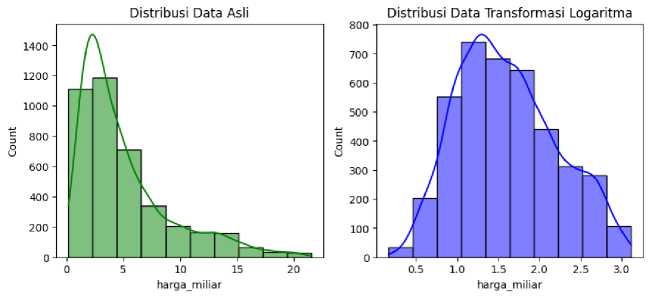
Gambar 7. Distribusi Data Target Asli dan Hasil Transformasi

Gambar 7 tersebut menjelaskan perbandingan visualisasi distribusi data asli dengan hasil transformasi pada variabel target harga_miliar. Dari gambar tersebut terlihat bahwa transformasi logaritma natural dapat mengubah distribusi asimetris mendekati distribusi normal.

Pada proses splitting data, dilakukan pembagian dengan perbandingan 80% data latih dan 20% data uji [16]. Pembagian data menghasilkan data latih sebanyak 3.192 baris dan 798 data uji. Proses pembagian ini dilakukan pada masing-masing skenario pemodelan.

Proses normalisasi data pada penelitian ini menggunakan teknik min-max scalling dengan kisaran nilai antara 0 dan 1. Normalisasi data dilakukan untuk menyamakan skala pada setiap atribut input [17]. Hal ini dilakukan sebagai salah satu upaya dalam mempercepat performa model yang akan dibangun dalam memahami pola-pola dalam data.

array([[0.25 0. [0.25 0.5 [0.25 0.5	, 0.13091483, 1. , 0.09621451, L , 0.18454259, L	0.24967148, 0.42857143, 0.33333333 0.13272011, 0.42857143, 0.5
		0.42049934, 0.28571429,		0.5
[0.75	, 0.14Θ37855,	0.18396846,	0.28571429,	0.5
0.	L
[0.25	, 0.28548896,	0.24967148,	0.57142857,	0.33333333
0.	L
[I-	, 0.15930599,	0.16557162,	0.28571429,	0.33333333
0.5	]])

Gambar 8. Data Hasil Normalisasi Min-Max Scalling

Gambar 8 menunjukkan hasil perubahan skala pada masing-masing variabel independen menjadi skala yang sama. Proses transformasi ini dilakukan untuk mempermudah proses pemodelan antara variabel independen dengan variabel target di dalam proses Model.

Parameter terbaik setelah grid search: {'C': 10, 'epsilon': 1, 'gamma': 1, 'kernel': 'rbf'}

Root Mean Squared Error (RMSE): 2.175646150188057

Mean Absolute Error (MAE): 1.3630525899121044

Mean Absolute Percentage Error (MAPE): 0.3224556491060808

R^2 Score: 9.7028737429175912

Gambar 9. Parameter Optimal dan Evaluasi Model Data Asli

Gambar 9 menunjukkan parameter optimal dari proses grid search dan hasil evaluasi model menggunakan data asli. Dilihat berdasarkan metrik R-Squared, model yang dihasilkan cukup baik dalam memodelkan data input dan data target.

Parameter terbaik setelah grid search: {'C': 1, 'epsilon': 9.1, 'gamma': 1, 'kernel': 'rbf'}

Root Mean Squared Error (RMSE): 0.2774275753583595

Mean Absolute Error (MAE): 0.20611210095739088

Mean Absolute Percentage Error (MAPE): 0.1452525638876444

R^λ2 Score: 0.7866721130857398

Gambar 10. Parameter Optimal dan Evaluasi Model Data Hasil Transformasi

Gambar 10 tersebut menunjukkan nilai evaluasi model menggunakan data hasil transformasi logaritma, yang mana hasil tersebut juga merupakan akibat dari parameter optimal metode grid search. Berdasarkan nilai error dari metrik RMSE, MAE, dan MAPE, kinerja dapat dikategorikan baik karena nilainya yang cenderung kecil.

• 3.5.    Interpret

Pada tahapan metodologi yang telah dilakukan, hasil dapat diinterpretasikan sebagai berikut:

• a.    Tahapan Obtain menggunakan teknik scrapping pada website rumah123.com menghasilkan data sebanyak 9.665 record. Dataset terdiri 10 atribut dengan kondisi data belum dilakukan pembersihan. Dataset yang terkumpul disimpan peneliti dengan format CSV dengan tujuan mempermudah proses analisis data selanjutnya.

• b.    Tahapan Scrub dilakukan proses pembersihan dan pengolahan data awal. Kegiatan ini dilakukan dengan memperhatikan faktor missing values, tidak konsisten format, dan data outlier. Hasil dataset berupa 7 kolom atribut dengan total data sebanyak 3.990 record. Atribut data terdiri dari lokasi, luas_tanah_m2, luas_bangunan_m2, kamar_tidur, kamar_mandi, kapasitas_garasi, dan harga_miliar.

• c.    Tahapan Explore dilakukan untuk mengetahui karakteristik data secara mendalam. Ditemukan indikasi distribusi data asimetris pada variabel luas_tanah_m2, luas_bangunan_m2, dan harga_miliar. Hal ini ditandai dengan kebanyakan data berkumpul pada nilai yang lebih rendah dan mendekati nilai nol. Nilai korelasi Pearson variabel bebas terhadap variabel target mayoritas positif terkecuali atribut lokasi.

• d.    Tahapan Model yang dilakukan menggunakan dua skenario data, data asli dan data hasil transformasi logaritma pada variabel target. Hal ini didasari distribusi data yang asimetris. Pada evaluasi model, data asli menghasilkan metrik RMSE = 2.175646150188057, MAE =  1.3630525890121044, MAPE =  0.3224556491060808, dan R-Squared =

0.7028737429175912 dengan parameter optimal Cost = 10, epsilon = 1, dan gamma = 1. Data hasil transformasi menghasilkan RMSE = 0.2774275753583595, MAE = 0.20611210095739088, MAPE =  0.1452525638876444,  dan R-Squared =

0.7866721130857308 dengan parameter optimal Cost = 1, epsilon = 0.1, dan gamma = 1.

• 4.    Kesimpulan

Berdasarkan hasil dari seluruh tahapan penelitian, dapat ditarik kesimpulan sebagai berikut:

• a.    Model terbaik dan parameter optimal dihasilkan dari skenario data hasil transformasi logaritma. Hal tersebut berdasarkan nilai metrik koefisiensi determinasi yang baik dengan nilai metrik error yang cenderung kecil dibandingkan model data asli. Model tersebut menghasilkan RMSE = 0.2774275753583595, MAE = 0.20611210095739088, MAPE = 0.1452525638876444, dan R-Squared = 0.7866721130857308 dengan parameter

optimal Cost = 1, epsilon = 0.1, dan gamma = 1.

• b.    Berdasarkan hasil model terbaik, kualitas data sangat berpengaruh terhadap akurasi model yang dihasilkan. Kesimpulan ini didukung oleh penelitian sebelumnya yang menyatakan bahwa pengolahan data awal sangat mempengaruhi tingkat akurasi dari model yang dihasilkan [1].

• c.    Distribusi data simetris berperan dalam peningkatan akurasi model. Hal ini terbukti dari perbedaan hasil evaluasi dari kedua skenario pemodelan, distribusi yang lebih simetris menghasilkan nilai metrik yang lebih baik. Hasil penelitian ini juga telah terbukti pada penelitian sebelumnya dengan objek teliti yang berbeda [15].

References

• [1]    A. Saiful, S. Andryana, eta A. Gunaryati, «Prediksi Harga Rumah Menggunakan Web Scrapping dan Machine Learning Dengan Algoritma Linear Regression», JATISI (Jurnal Tek. Inform. dan Sist. Informasi), libk. 8, zenb. 1, or. 41–50,  2021, doi:

10.35957/jatisi.v8i1.701.

• [2]    F. R. Lumbanraja, R. A. Saputra, K. Muludi, A. Hijriani, eta A. Junaidi, «Implementasi Support Vector Machine dalam Memprediksi Harga Rumah pada Perumahan di Kota Bandar Lampung», J. Pepadun, libk. 2, zenb. 3, or. 327–335,  2021, doi:

10.23960/pepadun.v2i3.90.

• [3]    Z. Rais, R. Isnaeni, eta Sudarmin, «Analisis Support Vector Regression (SVR) Dengan Kernel Radial Basis Function (RBF) Untuk Memprediksi Laju Inflasi Di Indonesia», VARIANSI J. Stat. Its Appl. Teach. Res., libk. 4, zenb. 1, or. 30–38, 2022, doi: 10.35580/variansiunm13.

• [4]    G. H. Saputra, A. H. Wigena, eta B. Sartono, «Penggunaan Support Vector Regression Dalam Pemodelan Indeks Saham Syariah Indonesia Dengan Algoritme Grid Search», Indones. J. Stat. Its Appl., libk. 3, zenb. 2, or. 148–160, 2019, doi: 10.29244/ijsa.v3i2.172.

• [5]    T. Prasetiya, I. Ali, C. L. Rohmat, eta O. Nurdiawan, «Klasifikasi Status Stunting Balita Di Desa Slangit Menggunakan Metode K-Nearest Neighbor», INFORMATICS Educ. Prof. J. Informatics, libk. 5, zenb. 1, or. 93, 2020, doi: 10.51211/itbi.v5i1.1431.

• [6]    Syafi’i, O. Nurdiawan, eta G. Dwilestari, «Penerapan Machine Learning Untuk Menentukan Kelayakan Kredit Menggunakan Metode Support Vektor Machine», J. Sist. Inf. dan Manaj., libk. 10, zenb. 2, or. 1–6, 2022.

• [7]    D. I. Purnama, «Peramalan Jumlah Penumpang Berangkat Melalui Transportasi Udara di Sulawesi Tengah Menggunakan Support Vector Regression (SVR)», Jambura J. Math., libk. 2, zenb. 2, or. 49–59, 2020, doi: 10.34312/jjom.v2i2.4458.

• [8]    H. Yasin, A. Prahutama, eta T. W. Utami, «Prediksi Harga Saham Menggunakan Support Vector Regression Dengan Algoritma Grid Search», Media Stat., libk. 7, zenb. 1, or. 29– 35, 2014, doi: 10.14710/medstat.7.1.29-35.

• [9]    R. E. Cahyono, J. P. Sugiono, eta S. Tjandra, «Analisis Kinerja Metode Support Vector Regression (SVR) dalam Memprediksi Indeks Harga Konsumen», J. Teknol. Inf. dan Multimed., libk.  1, zenb. 2, or. 106–116,  2019, [Sarean]. Available at:

www.siskaperbapo.com

• [10]    N. D. Maulana, B. D. Setiawan, eta C. Dewi, «Implementasi Metode Support Vector Regression (SVR) Dalam Peramalan Penjualan Roti (Studi Kasus : Harum Bakery)», J. Pengemb. Teknol. Inf. dan Ilmu Komput. , libk. 3, zenb. 3, or. 2986–2995, 2019.

• [11]    O. Nurdiawan, A. Irma Purnamasari, eta I. Ali, «Analisa Penjualan Mobil Dengan Menggunakan Algoritma K-Means Di PT. Mulya Putra Kencana», J. Data Sci. dan Inform., libk. 1, zenb. 2, or. 32–35, 2021.

• [12]    K. R. Putra, S. Umaroh, N. Fitrianti, eta S. Nugraha, «RESULTANT: Data Preparation Techniques to Improve XGBoost Algorithm Performance», MIND (Multimedia Artif. Intell. Netw. Database) J., libk. 8, zenb. 1, or. 42–51, 2023.

• [13]    F. Firmansyah eta O. Nurdiawan, «Penerapan Data Mining Menggunakan Algoritma Frequent Pattern - Growth Untuk Menentukan Pola Pembelian Produk Chemicals», JATI (Jurnal Mhs. Tek. Inform., libk. 7, zenb. 1, or. 547–551, 2023, doi: 10.36040/jati.v7i1.6371.

• [14]    I. Setiawan, R. Fina Antika Cahyani, eta I. Sadida, «EXPLORING COMPLEX DECISION TREES : UNVEILING DATA PATTERNS AND OPTIMAL PREDICTIVE POWER», J. Innov. Futur. Technol., libk. 5, zenb. 2, or. 112–123, 2023.

• [15]    D. Wasani eta S. I. Purwanti, «The GRDP Per Capita Gap between Provinces in Indonesia and Modeling with Spatial Regression», J. Mat. Stat. dan Komputasi, libk. 19, zenb. 1, or. 65–78, 2022, doi: 10.20956/j.v19i1.20997.

• [16]    P. Putriyana eta O. Nurdiawan, «Implementasi Data Mining Untuk Memprediksi Kelulusan Siswa SMK Al Huda Kedungwungu Dengan Menggunakan Algoritma Naïve Bayes Classifier», Exp. Student Exp., libk. 1, zenb. 1, or. 1–7, 2023.

• [17]    A. Toha, P. Purwono, eta W. Gata, «Model Prediksi Kualitas Udara dengan Support Vector Machines dengan Optimasi Hyperparameter GridSearch CV», Bul. Ilm. Sarj. Tek. Elektro, libk. 4, zenb. 1, or. 12–21, 2022, doi: 10.12928/biste.v4i1.6079.

696