PENGARUH VOLUME PERDAGANGAN SAHAM, NILAI TUKAR DAN INDEKS HANG SENG TERHADAP PERGERAKAN INDEK HARGA SAHAM GABUNGAN

PENGARUH VOLUME PERDAGANGAN SAHAM, NILAI TUKAR DAN INDEKS HANG SENG TERHADAP PERGERAKAN INDEK HARGA SAHAM GABUNGAN

Fikri Mutakif¹

2

Andini Nurwulandari²

¹Fakultas Ekonomi Universitas Nasional Jakarta(UNJ), Indonesia e-mail: andin_manajemen@yahoo.com

²Fakultas Ekonomi Universitas Nasional Jakarta(UNJ), Indonesia e-mail: andin_manajemen@yahoo.com

ABSTRAK

Pada pemodelan TARCH (2,2) dapat dibuktikan bahwa volume perdagangan saham berpengaruh positif dan signifikan terhadap IHSG. Indeks Hang Seng berpengaruh positif dan signifikan terhadap IHSG. Kurs USD-Rp berpengaruh negatif dan signifikan terhadap IHSG. Berdasarkan hasil prediksi yang diperoleh dari model GARCH dan ARIMA, terlihat bahwa model ARIMA memberikan hasil selisih nilai terkecil antara faktual dan prediksi dibandingkan dengan model GARCH . Sehingga dapat disimpulkan bahwa model ARIMA berbeda dengan GARCH. Untuk data yang dihadapi saat ini, metode ARIMA dapat digunakan untuk memprediksi pergerakan IHSG karena mempunyai kesalahan lebih kecil.

Kata kunci: Volume perdagangan, Indeks Hang Seng, Kurs USD-Rp, IHSG, ARIMA, GARCH, TARCH.

ABSTRACT

In the modeling TARCH (2.2), it can be proved that the volume of stock trading has positive and significant impact on JKSE. Hang Seng Index has positive and significant impact on JKSE. USD – Rp exchange rate has negative and significant impact on JKSE. Based on the predicted results obtained from GARCH and ARIMA models, it shows that ARIMA models provide the smallest value of the difference between factual and predictions compared to GARCH model. So it can be concluded that ARIMA models are different from GARCH. To analyze the current data, ARIMA methods should be used to predict the movement JKSE because it has a smaller error.

Keywords : Trading volume, Hang Seng Index, Currency USD-IDR, JKSE, ARIMA, GARCH, TARCH.

PENDAHULUAN

Salah satu investasi yang mulai banyak diminati oleh masyarakat adalah investasi saham, karena saham cenderung memberikan keuntungan dalam waktu singkat dibandingkan dengan jenis

investasi yang lain. Harga saham sangat penting bagi para investor, karena memiliki konsekuensi ekonomi. Ketika volume perdagangan saham menurun maka harga saham juga akan menurun. Sebaliknya ketika volume perdagangan

saham meningkat maka harga saham juga akan meningkat.

Perubahan volume perdagangan saham akan berpengaruh terhadap Indeks Harga Saham Gabungan (IHSG) yang pada akhirnya mengubah kesejahteraan investor. Semakin besar volume transaksi saham yang dilakukan oleh investor di pasar modal menyebabkan peningkatan terhadap IHSG. Sebaliknya, semakin kecil volume transaksi saham yang dilakukan oleh investor di pasar modal menyebabkan penurunan IHSG. Perubahan IHSG mencerminkan perkembangan perusahaan atau industri suatu negara. Indeks harga saham yang mengalami penurunan dapat disebabkan oleh kondisi perekonomian di negara tersebut yang sedang mengalami permasalahan. Sebaliknya, indeks harga saham yang mengalami peningkatan dapat mengindikasikan adanya perbaikan kinerja perekonomian di negara tersebut.

Tindakan investasi tidak terlepas dari risiko, risiko tersebut dapat kita lihat dari pergerakan mata uang asing di Indonesia. Nilai tukar mata uang asing memiliki hubungan yang dinamis dengan

harga saham. Hubungan kurs dengan pasar modal memiliki korelasi. Saat kurs meningkat atau nilai tukar USD terhadap rupiah menguat maka IHSG akan menurun, sebalik nya saat kurs menurun atau nilai tukar USD terhadap rupiah melemah maka IHSG akan meningkat. Hal ini disebabkan karena saat kurs asing meningkat para investor akan cenderung melakukan investasi dalam bentuk mata uang asing di bandingkan investasi di pasar saham.

Hubungan bilateral dan perdagangan antar negara juga memiliki keterkaitan dengan harga saham domestik, negara yang perekonomiannya kuat akan mempengaruhi negara yang perekonomian lebih lemah. Negara yang perekonomiannya kuat saat ini adalah China, sedangkan negara yang lebih lemah adalah Indonesia. Dalam lima tahun ke depan, nilai perdagangan Indonesia-China di perkirakan akan mencapai US$ 50 miliar. Peningkatan hubungan bilateral tersebut, tidak terlepas dari terjalinnya Free Trade Asean-China. Adapun struktur perdagangan Indonesia-China 2003-2009 sebagai berikut.

Tabel 1: Struktur Perdagangan Indonesia-China, 2003-2009 (%)

URAIAN	2003	2004	2005	2006	2007	2008	2009
EKSPOR    (Juta USD)	3803	4605	6662	8344	9676	10295	9055.0
Minyak dan Gas	25.9	25.4	40.57	34.5	31.1	34.2	24.5
Industri	49.0	48.8	36.91	40.0	40.5	38.6	42.3
Pertanian	7.7	8.5	8.05	9.0	10.3	9.9	12.2
Pertambangan	17.4	17.3	14.48	16.5	18.1	17.2	21.1
IMPOR (Juta USD)	2958	4101	5843	6637.0	8558	13108	11020
Minyak dan Gas	21.0	18.1	22.1	17.1	7.0	1.8	2.4
Industri	63.8	66.2	63.5	67.2	75.9	79.6	80.1
Pertanian	11.6	15.5	13.8	15.4	16.5	18.0	17.2
Pertambangan	3.6	0.2	0.6	0.2	0.6	0.6	0.2

Sumber: Adam Latif (2011)

Peningkatan nilai perdagangan itu didasarkan pada semakin meningkat nya hubungan ekonomi Indonesia-China, yang tidak hanya meliputi bidang perdagangan barang dan jasa, tetapi juga investasi lainnya, seperti perhotelan dan

jasa-jasa lainnya. Selain gambaran tentang struktur perdagangan antara Indonesia dan China, berikut akan disajikan perkembangan bursa saham antara kedua negara tersebut, yaitu:

Tabel 2 : Perkembangan Pasar Modal China dan Indonesia

Tahun	Kapitalisasi Pasar (USD)		Indeks Harga Saham
	China	Indonesia	Hang Seng	IHSG
2007	6,226,305,290,000	211,692,970,000	27,812.65	2,745.83
2008	2,793,612,600,029	98,760,599,266	14,387.48	1,355.41
2009	5,007,646,096,891	178,190,945,564	21,872.50	2,534.36
2010	4,762,836,764,951	360,388,099,886	23,035.45	3,703.51
2011	3,389,098,223,398	390,106,865,178	18,434.39	3,821.99

Sumber: Worldbank (2012) .

Jika dilihat perkembangan pasar modal di China, maka kapitalisasi pasarnya jauh lebih besar disbanding kan Indonesia, begitupula dengan perkembangan indeks Hang Seng. Pada perekonomian yang makin terbuka, serta semakin pesatnya perkembangan teknologi, membuat kejadian disuatu bursa dapat segera diketahui sehingga mempengaruhi bursa lain. Dalam hal ini, bursa yang mempunyai kapitalisasi pasar yang lebih besar (kuat) akan mempengaruhi bursa yang lebih lebih kecil (rendah) (Nachrowi dan Usman 2006).

Penelitian tentang pengaruh bursa asing asing pada bursa saham Indonesia telah banyak dilakukan. Prediksi pergerakan IHSG dengan menggunakan metode GARCH dan ARIMA, menunjukkan bahwa model ARIMA memiliki tingkat kesalahan yang lebih kecil dibandingkan model GARCH. Pada penelitian ini Nahrowi Djalal dan Usman hanya memprediksi IHSG menggunakan metode GARCH dan ARIMA (Nahrowi dan Usman, 2007).

Pengaruh volume perdagangan saham, deposito, dan kurs terhadap IHSG

serta prediksi IHSG meng gunakan metode GARCH dan ARIMA dilakukan oleh Murwaningsari (2008), ditemukan bahwa volume perdagangan saham dan suku bunga berpengaruh positif terhadap IHSG, sedangkan kurs tidak memiliki pengaruh yang signifikan. Begitupun dengan prediksi IHSG menggunakan metode ARIMA memiliki tingkat kesalahan yang lebih kecil dibandingkan metode GARCH. Pada penelitian ini Murwaningsari (2008) belum mengikut sertakan indeks Hang Seng dalam penelitiannya, sementara dominansi kekuatan perekonomian China yang dicerminkan indeks Hang Seng diduga semakin meningkat, dan menjadi acuan untuk para investor di seluruh dunia.

Pada penelitian ini penulis mencoba meneliti pengaruh volume perdagangan saham, kurs USD-Rp, dan indeks Hang Seng terhadap pergerakan IHSG, serta prediksi IHSG dengan metode GARCH dan ARIMA. Dalam penelitian ini penulis menambahkan indeks Hang Seng, karena pada penelitian sebelumnya sepanjang pengetahuan penulis belum dilakukan penelitian mengenai pengaruh indeks

Hang Seng terhadap IHSG dengan menggunakan metode GARCH dan ARIMA.

Kajian Pustaka

Metode analisis yang digunakan, metode GARCH dan ARIMA (Nachrowi dan Usman, 2006):

• a.    Metode ARCH-GARCH

Model ARCH dan GARCH memanfaatkan heteroskedastisitas untuk membuat model. Ada 2 model pada jenis ARCH, yaitu ARCH (1) dan ARCH (p). Model ARCH(1) dinyatakan sebagai berikut :

Ot =   + αι⅛ i ……….... (2.3)

Model ARCH(p) dinyatakan sebagai berikut :

Ot =   + ∑LiOie_t i………… (2.4)

Pada    model    ARCH(p)

heteroskedastisitas tergantung pada volatilitas beberapa periode lalu. Agar varian menjadi positif, maka harus dibuat pembatasan, yaitu :  ¾ >

0 dan0<a₁<1

Seperti pada ARCH diatas, metode GARCH juga memiliki dua model, yaitu GARCH(1,1) dan GARCH(p,q). Dimana model GARCH (1,1) dapat dinyatakan sebagai berikut

Ot =   + a₁eLι + ⅛-ι    ...

…………………………………(2.5)

Model ini dinamakan model GARCH(1,1) karena ^σt tergantung pada ^et-ι dan Ot-I yang masing-masing mempunyai lag waktu sama. Pada model ini juga dibuat pembatasan agar varian menjadi positif, yaitu

• :   > 0; cc^ dan Λ^ ≥ 0; dan a^ +

λ₁<1

Sedangkan model GARCH(p,q) dapat dinyatakan sebagai berikut :

al = +∑Li ^ai e^_i ^∑Li^i^aLi ……………………………… (2.6)

Yang membedakan antara model ARCH dan GARCH adalah pola atau model dari varian error-nya.

• b.    Metode ARIMA

Metode ARIMA sering juga disebut metode runtun waktu Box-Jenkins. ARIMA sangat baik ketepatannya untuk peramalan jangka pendek. Model ARIMA dituliskan dengan notasi ARIMA

(p,d,q). p adalah derajat proses AR, d adalah orde pembedaan, dan q adalah derajat proses MA. Adanya nilai pembedaan (d) pada model ARIMA disebabkan aspek-aspek AR dan MA hanya dapat diterapkan pada data time series yang stasioner.

• 1)    Autoregressive Model (AR)

Model AR mempunyai ordo yang besarnya dinotasikan dengan huruf p, pengamatan yt dibentuk dari rata-rata tertimbang pengamatan-pengamatan masa lalu, p periode kebelakang dan deviasi periode sekarang. Bentuk umum model AR(p) dinyatakan sebagai berikut:

yt=Ø1 yt-1 +Ø2 yt-2 + … + Øp yt-p + δ + et...……….………. (2.6)

dimana:

yt = suatu konstanta

Øp = parameter autoregresif kep

Et = nilai kesalahan pada saat t 2) Moving Average Model (MA)

Model MA mempunyai ordo yang besarnya di notasikan dengan huruf q, model ini mengasumsikan bahwa tiap-tiap observasi dibentuk dari rata-rata tertimbang deviasi q periode kebelakang. Bentuk umum model AR(p) dinyatakan sebagai berikut:

yt =μ + et – 01et-1- 02et-2 - ... - 0qet-k ………….......(2.7)

dimana:

μ ' = suatu konstanta θ1sampai  θqadalah  parameter

parameter moving average

et-k= nilai kesalahan pada saat t – k

et = nilai kesalahan pada saat t

• 3)    Model campuran

• a)    model ARMA

Model umum untuk campuran proses AR(p) dan MA(q), model ini didekati dengan model campuran antara otoregresi dan moving average yang dikenal dengan model ARMA(p,q). Model ini dapat dinyatakan sebagai berikut: yi = 0ιy_t - i h-----+ 0p yt-p + s + eι^-θi^et - i-----0q^et - _q

…………………..….(2.8)

• b)    model ARIMA

Model umum ARIMA (p,d,q) akan terpenuhi jika nonstasioneritas ditambah kan pada campuran proses ARMA.

Model ersebut dapat dinyatakan sebagai berikut: 0(B) ∆^dy_i = S + Θ(B)e_t ………….. (2.9)

Musiman model ARIMA didefinisikan sebagai suatu pola yang berulang - ulang dalam selang waktu yang tetap. Untuk mengenali adanya faktor musiman, harus melihat pada autokorelasi yang tinggi. Untuk menangani musiman, notasi umum yang singkat adalah:

ARIMA (p,d,q) (P,D,Q)^S Dimana

(p,d,q)  = bagian yang tidak

musiman dari model

(P,D,Q) = bagian musiman dari model

S       = jumlah periode per

musim

Rerangka Konseptual dan Hipotesis

Dalam penelitian ini, penulis membatasi hanya membahas variabel volume perdagangan saham, indeks Hang Seng, nilai tukar USD terhadap Rupiah pengaruhnya terhadap IHSG.

Berikut ditunjukkan rerangka konseptual pada Bagan 3.1 dan 3.2

Pendekatan GARCH

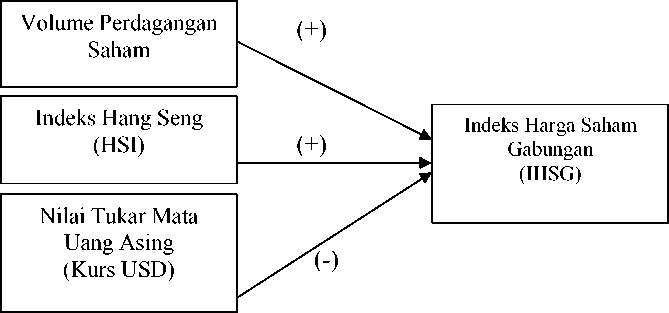
Bagan 1

Rerangka Konseptual GARCH

Bagan 3.1 menunjukkan adanya pengaruh positif dari volume perdagangan saham terhadap IHSG, yaitu semakin tinggi volume perdagangan saham maka akan semakin tinggi IHSG, sebaliknya semakin rendah volume perdagangan saham akan semakin rendah IHSG. Indeks Hang Seng juga memiliki pengaruh positif terhadap IHSG, semakin tinggi indeks Hang Seng maka akan semakin tinggi IHSG, sebaliknya semakin rendah indeks Hang Seng akan semakin rendah IHSG. Hal ini disebabkan oleh hubungan perdagangan antara Indonesia dengan Cina, yang melihat perkembangan perekonomian di Cina yang digambarkan melalui Indeks Hang Seng. Nilai tukar mata uang asing

(kurs USD-Rp) memiliki pengaruh negatif terhadap IHSG, artinya ketika nilai tukar USD mengalami penguatan terhadap Rupiah maka IHSG akan menurun, sebaliknya ketika nilai tukar USD terhadap Rupiah mengalami penurunan maka IHSG akan meningkat.

Pendekatan ARIMA

Bagan 3.2 menunjukan pergerakan IHSG dalam jangka pendek. IHSGt-n, IHSGt-2, IHSGt-1 merupakan pergerakan Indeks setiap harinya yang terus berubah dan mempengaruhi IHSG. Sedangkan Residualt-n, Residualt-2, Residualt-1 juga merupakan faktor yang mempengaruhi IHSG setiap harinya (Murwaningsih, 2008).

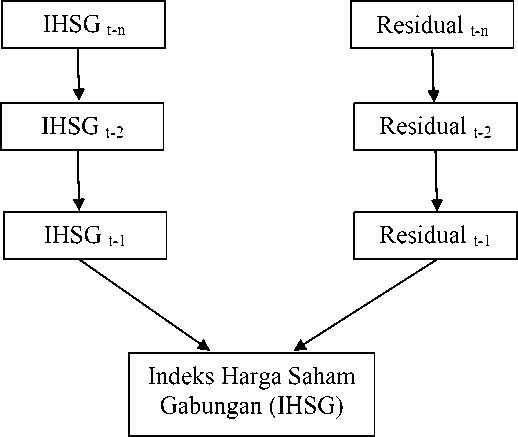
Bagan 2

Rerangka Konseptual ARIMA

METODE PENELITIAN

Sampel penelitian adalah data harian Indeks Harga Saham Gabungan (IHSG) di Indonesia, volume perdagangan saham, kurs USD terhadap Rupiah, dan indeks Hang Seng. Periode penelitian 2001- 2010.

Untuk mendukung penelitian ini, diperlukan data dan informasi yang relevan guna mendapatkan gambaran yang jelas dan nyata terhadap objek yang diteliti. Sumber data yang diperoleh merupakan data dokumentasi dari Pusat Referensi Pasar Modal (PRPM) di Bursa Efek Indonesia (BEI) dan www.Yahoo

finance.com untuk IHSG harian, volume saham IHSG harian, dan indeks Hang Seng harian. Sementara untuk data kurs berasal dari web Bank Indonesia yaitu www.bi.go.id.

Di dalam penelitian ini, Vaiabel Operasional yang digunakan adalah:

• a.    Indeks Harga Saham Gabungan

(IHSG) adalah IHSG harian.

• b.    Volume perdagangan saham adalah Ln jumlah lembar saham yang diperdagangkan di bursa secara harian.

• c.    Indeks Hang Seng adalah indeks saham harian yang dihitung berdasarkan kapitalisasi pasar saham di Hong Kong

• d.    Kurs adalah nilai tukar USD terhadap Rupiah harian yaitu kurs tengah.

Model Penelitian

Model Ordinary Least Square (OLS)

Model ini dipilih karena sifatnya hanya satu arah yaitu dari tiga variabel yang terpilih terhadap IHSG. Sedangkan arah kebalikannya diasumsikan tidak terjadi. Maka model penelitian secara matematis dapat dituliskan sebagai berikut:

=  +    +

+     +

Dimana :

IHSG = Indeks Harga Saham Gabungan

Vol = Volume Perdagangan Saham

KURS = Nilai tukar USD terhadap Rupiah

HSI   = Indeks Hang Seng

e     = Mempresentasikan

variabel lain yang mempengaruhi IHSG tetapi tidak secara eksplisit terpilih dalam model

β      = Parameter dari model

yang besarnya akan diestimasi

Model ARCH-GARCH

Model ini dapat digunakan dengan syarat adanya heteroskedastisitas dalam error dengan tepat. Langkah pertama adalah menguji ARCH effect, setelah itu dilakukan pengujian dengan menggunakan lag sehingga tidak terdapat lagi ARCH effect. Apabila belum terdapat model yang tepat maka dilakukan trial and error atau mencoba beberapa kemungkinan model, sehingga mendapatkan model terbaik.

Setelah model terbaik didapatkan, barulah dilakukan peramalan dengan menggunakan persamaan sebagai berikut

ARCH(p)         =+

^∑

GARCH(p,q)         =+

^∑+∑

Dimana :

= varian residual sebagai fungsi dari volatilitas dan varian residual masa lalu.

= Konstanta

a_ie_t _ ₁  = Komponen ARCH(p)

= Komponen GARCH(p,q)

Model ARIMA

Model ini dapat dikatakan sebagai metode pendekatan pola yang memprediksi pergerakan indeks harga saham melalui pola pergerakan indeks harga saham itu sendiri. Pendekatan ini lebih mengandalkan argumen bahwa pergerakan variabel yang diamati sudah mencerminkan semua informasi yang mempengaruhi per gerakannya.

Model ARIMA umumnya dituliskan dengan notasi ARIMA (p,d,q). p adalah derajat proses AR, d adalah orde pembedaan, dan q adalah derajat proses MA. Adanya nilai pembedaan (d) pada model ARIMA disebabkan aspek-aspek AR dan MA hanya dapat diterapkan pada data time series yang stasioner.

Secara matematis model ini dibentuk sebagai berikut :

V_t =  + βι^t-ι + β2 ^1-2 … + β^t-n

+ Yιε_t-ι+⋯+Y3εt-_n

Dimana : Y_t = IHSG ^εt = Residual

HASIL DAN PEMBAHASAN

Deskripsi Hasil Penelitian

Kenaikan rata-rata harga IHSG umumnya ke arah yang positif, dapat dilihat pada tahun 2001 hingga 2010, namun tahun 2008 hingga 2009 harga saham menurun dengan nilai sebesar 9.02%. Penurunan-penurunan harga saham ini disebabkan karena krisis finansial dunia pada pertengahan tahun 2008.

Rata-rata kenaikan indeks Hang Seng bergerak fluktuatif, dapat dilihat pada tahun 2001 dan 2002. Pada tahun 2003 hingga 2004 sempat meningkat akan tetapi di tahun 2005 kembali menurun, hingga akhirnya terus meningkat dalam 3 tahun, sejak 2006 hingga 2008 indeks Hang Seng terus meningkat. Tapi setelah 2008 hingga 2009 indeks Hang Seng menurun drastis dengan nilai sebesar 29% . Penurunan

indeks Hang Seng ini disebabkan karena krisis finansial dunia pada pertengahan tahun 2008 hingga 2009.

Rata-rata volume perdagangan IHSG fluktuatif, dapat dilihat pada tahun 2001 hingga 2007. Tahun 2008 sampai dengan 2009, volume perdagangan IHSG meningkat drastis hingga mencapai nilai transaksi 595,71%. Selama 2001 hingga 2010, Rata-rata kenaikan kurs USD terhadap Rp fluktuatif. Tetapi mulai menguat lagi hingga 2005. Pada akhirnya mencapai angka penurunan kurs USD terhadap Rp yang paling rendah di tahun 2010, yang diakibatkan kondisi pasar global dunia. Jika nilai tukar USD pada Rupiah menguat, maka indeks harga saham di Indonesia turun.

Uji Perilaku Data

Langkah awal dari penelitian data time series yaitu dengan menguji kestasioneritasan data dari masing-masing variabel.

Uji stasioneritas data dilakukan dengan dua tahap yaitu pertama melalui uji akar-akar unit dan kedua melalui derajat integrasi. Metode yang digunakan untuk uji akar-akar unit maupun uji derajat integrasi dengan uji Phillips-Perron. Uji derajat integrasi akan dilakukan jika data belum stasioner pada derajat nol (level). Hasil uji akar unit dan derajat integrasi dapat dilihat pada Tabel 4.2sebagai berikut :

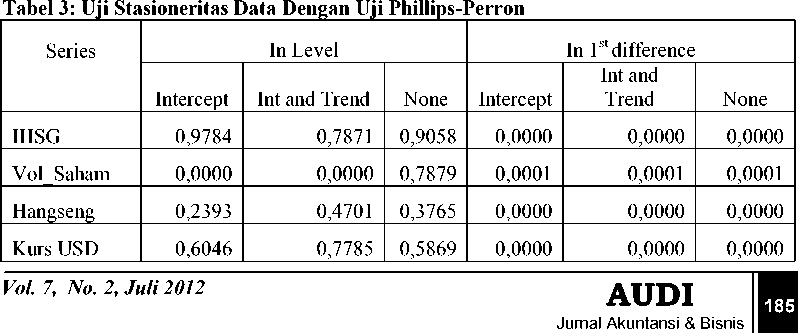
Berdasarkan hasil uji stasioneritas data pada Tabel 4.2 dapat terlihat bahwa data masih belum stasioner, ini terlihat dari nilai probabilitas PP yang lebih besar dari alpha (α) 5%. Data yang

belum stasioner kemudian dilakukan uji derajat integrasi 1 (first difference). Hasil uji derajat integrasi menunjukkan bahwa semua data telah stasioner pada derajat integrasi 1 (first difference).

Model OLS

Berdasarkan hasil uji stasioneritas, data-data  penelitian  sebagian  besar

ternyata tidak stasioner. Karena itu, data-data tersebut tidak tepat dianalisis dengan menggunakan metode ordinary least square (OLS) yang mensyaratkan stasioneritas asli atau yang belum dimanipulasi. Apabila data-data yang tidak stasioner tetap digunakan dalam proses analisis dengan metode OLS, hal itu akan menghasilkan spurious regression. Hasil estimasi model regresi biasa dengan OLS yang menggunakan data tidak stasioner akan menghasilkan estimasi yang spurious regression dapat dilihat pada Tabel 4.3

Tabel 4 : Model OLS sederhana

Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	1635.582	440.7052	3.711283	0.0002
VOL_SAHAM	143.6739	8.137926	17.65486	0.0000
HANSENG	0.050710	0.006260	8.100462	0.0000
KURS	-0.338953	0.025939	-13.06711	0.0000
R-squared	0.798945	Mean dependent	var	2367.921
Adjusted R-squared	0.798073	S.D. dependent var		644.6974
S.E. of regression	289.7028	Akaike info criterion		14.18132
Sum squared resid	58077993	Schwarz criterion		14.20744
Log likelihood	-4931.099	F-statistic		916.6146
Durbin-Watson stat	0.184254	Prob(F-statistic)		0.000000

Berdasarkan Tabel 4.3 tersebut terlihat bahwa hasil regresi dengan metode OLS menghasilkan estimasi spurious regression. Hal ini terlihat dari nilai R² yang tinggi (0,79) disertai oleh nilai Durbin Watson statistik yang lebih rendah (0,18). Estimasi spurious regression mengakibatkan koefisien regresi penaksir tidak efisien, peramalan akan regresi tersebut akan meleset, dan uji baku yang umum untuk koefisien regresi menjadi invalid. Suatu regresi dikatakan spurious regression apabila asumsi klasik tidak terpenuhi. Asumsi

ini dapat diketahui dengan melakukan uji asumsi klasik terhadap model ini, yang antara lain terdiri atas uji normalitas, uji multikolinieritas, uji autokolerasi dan uji heteroskedastisitas.

Uji ARCH LM

Menurut Engle dalam Widarjono 2005), adanya volatilitas data tersebut mengindikasikan bahwa hasil estimasi tersebut terkena gejala ARCH effect. Adanya gejala ARCH effect tersebut dapat dibuktikan dengan signifikansi hasil uji ARCH LM.

Tabel 5: Uji ARCH LM

ARCH Test:

F-statistic	1495.523	Probability	0.000000
Obs*R-squared	474.9269	Probability	0.000000

Apabila nilai probilitas (p-value) pada F statistic lebih kecil dari nilai signifikansi (α = 5%) maka terdapat ARCH effect, sebaliknya apabila nilai probilitas (p-value) pada F statistic lebih besar dari nilai signifikansi (α = 5%) maka tidak terdapat ARCH effect. Pada tabel 4.6 menunjukan nilai probabilitas pada F statistic (0.000000) lebih kecil dari nilai signifikansi (α = 5%) maka dapat dikatakan data memiliki ARCH effect. Dengan demikian estimasi model dapat menggunakan ARCH/GARCH.

Pemilihan Model Terbaik

Berdasarkan hasil pengujian terhadap asumsi klasik dan terdapatnya ARCH effect dalam data yang dianalisis. Maka peneliti akan menggunakan model ARCH/GARCH. Dalam penelitian ini peneliti menggunakan model GARCH (1,1), yang merupakan model paling umum dari model ARCH/GARCH. Model GARCH(1,1) memperhatikan varian tak bersyarat (ARCH) dan varian bersyarat      (GARCH)      periode

sebelumnya.

Hasilnya tampak pada tabel 4.7 sebagai berikut :

Tabel 6: Model GARCH (1,1)

Coefficient

Std. Error      z-Statistic        Prob.

C	6993.647	191.9468	36.43535	0.0000
VOL_SAHAM	29.53596	2.612976	11.30357	0.0000
HANSENG	-0.015840	0.002755	-5.749799	0.0000
KURS	-0.508046	0.010709	-47.43948	0.0000
Variance Equation
C	629.5119	217.5412	2.893759	0.0038
ARCH(1)	0.782409	0.130639	5.989092	0.0000
GARCH(1)	0.256248	0.068088	3.763464	0.0002
R-squared	0.684729	Mean dependent var		2367.921
Adjusted R-squared	0.681984	S.D. dependent var		644.6974
S.E. of regression	363.5638	Akaike info criterion		13.06901
Sum squared resid	91071084	Schwarz criterion		13.11473
Log likelihood	-4541.016	F-statistic		249.4037
Durbin-Watson stat	0.028418	Prob(F-statistic)		0.000000

Pada tabel 4.7 variabel GARCH(1,1) sudah signifikan, serta memiliki nilai Adjusted R-squared lebih besar, sementara nilai Schwarz lebih kecil.

Berikutnya peneliti mencoba model lain untuk mendapatkan model yang lebih baik dibandingkan dengan model GARCH(1,1) dan GARCH (2,2). Model GARCH (2,2) memiliki probabilitas yang sudah signifikan untuk semua variabel independen. Begitupula untuk nilai R², model GARCH(2,2) memiliki nilai R² paling besar diantara model-model yang lain.

Uji Asimetric Volatility (Model TARCH dan EGARCH)

Untuk mengetahui apakah terdapat asimetric volatility (leverage effect) maka digunakan model TARCH (Treshold ARCH) dan EGARCH (Exponential GARCH). Apabila dari model TARCH ataupun EGARCH ditemukan indikasi adanya asimetric volatility (leverage effect) maka model OLS-GARCH 2.2 yang merupakan model terbaik harus ditransformasikan ke dalam bentuk TARCH ataupun EGARCH.

Tabel 7 : Uji asimetric volatility menggunakan model TARCH dan EGARCH

Variance Equation	Probability
TARCH (RESID<0)*ARCH(1)	0.0369
EGARCH RES/SQR[GARCH](1)	0.4265

Menurut Widarjono (2005), dalam model TARCH ada tidaknya asimetric volatility (leverage effect) dapat dilihat dari persamaan varian yaitu variabel (RESID<0)*ARCH(1). Apabila nilai probability (RESID<0)* ARCH(1) kurang dari 0.05 maka terdapat asimetric

volatility (leverage effect), begitu pula sebaliknya. Berdasarkan hasil dari regresi model TARCH 2.2 pada Tabel 4.8 terlihat bahwa terdapat asimetric volatility (leverage effect), hal ini ditunjukkan oleh nilai probability (RESID<0)* ARCH(1) yang kurang dari 0.05.

Menurut Widarjono (2005), dalam model EGARCH ada tidaknya asimetric volatility (leverage effect) dapat dilihat dari persamaan varian yaitu variable |RES|/SQR [GARCH](1). Apabila nilai probability |RES|/SQR[GARCH](1) kurang dari 0.05 maka terdapat asimetric volatility (leverage effect), begitu pula sebaliknya. Berdasarkan hasil regresi model EGARCH (2.2) pada Tabel 4.8 terlihat bahwa tidak terdapat asimetric volatility (leverage effect), hal ini ditunjukkan oleh nilai probability |RES|/SQR [GARCH](1) yang lebih dari 0.05.

Dengan adanya asimetric volatility maka model OLS-GARCH 2.2 harus ditransformasikan menjadi model OLS-TARCH 2.2 (Treshold ARCH 2.2). Sehingga dapat disimpulkan bahwa model OLS-TARCH 2.2 (Treshold ARCH 2.2) merupakan model terbaik. Sebagai model terbaik, Model OLS- TARCH (2.2) akan menjadi dasar untuk menjelaskan faktor-faktor yang mempengaruhi hubungan variabel-variabel penelitian selama periode pengamatan.

Interpretasi Hasil

Setelah melakukan beberapa uji kelayakan model, maka model TARCH(2,2) terpilih menjadi model terbaik untuk digunakan dalam analisis ini. Berikut disajikan hasil regresi model yang terpilih.

Tabel 8 : Model TARCH(2,2)

	Coefficient	Std. Error	z-Statistic	Prob.
C	3578.676	214.8287	16.65828	0.0000
VOL_SAHAM	77.13224	2.792735	27.61889	0.0000
HANSENG	0.026428	0.003474	7.608283	0.0000
KURS	-0.351816	0.013929	-25.25801	0.0000
Variance Equation
C	18945.87	3321.896	5.703331	0.0000
ARCH(1)	0.960554	0.014970	64.16579	0.0000
ARCH(2)	0.966236	0.010288	93.91486	0.0000
(RESID<0)*ARCH(1)	-0.015705	0.018966	-0.828026	0.4077
GARCH(1)	-1.002292	0.012414	-80.73687	0.0000
GARCH(2)	-0.003940	0.012006	-0.328213	0.7428
R-squared	0.743102	Mean dependent var		2367.921
Adjusted R-squared	0.739732	S.D. dependent var		644.6974
S.E. of regression	328.9019	Akaike info criterion		13.26520
Sum squared resid	74209054	Schwarz criterion		13.33050
Log likelihood	-4606.289	F-statistic		220.4804
Durbin-Watson stat	0.053947	Prob(F-statistic)		0.000000

IHSG = 3578.67 + 77.13*VOL_SAHAM + 0.03*HANSENG - 0.35*KURS Persamaan variance (et): σt² = 18945.87+0.9605*e² t-1+0.9662*e²    t-2-    1,0022*σ²t-1    –

0,0039*σ²t-2

• a.    Pengaruh Volume Saham terhadap

IHSG

Berdasarkan   hasil   Estimasi

dengan menggunakan TARCH (2,2), terlihat bahwa volume saham memiliki pengaruh positif dan signifikan terhadap IHSG, bila volume perdagangan naik, indeks, IHSG akan naik. Hasil ini konsisten dengan penelitian Murwaningsari (2008) yang dapat membuktikan bahwa volume saham berpengaruh secara positif terhadap IHSG.

• b.    Pengaruh Indeks Hang Seng terhadap IHSG

Berdasarkan hasil estimasi dengan menggunakan TARCH (2,2), terlihat bahwa Hang Seng memiliki pengaruh yang positif dan signifikan terhadap IHSG. Artinya apabila Hang Seng naik maka akan diikuti oleh kenaikan IHSG. Diasumsikan membaiknya (memburuk nya) perekonomian China akan berdampak langsung terhadap perekonomian Indonesia, sehingga Hang Seng akan berpengaruh positif dan signifikan pada IHSG. Dengan demikian perubahan Hangseng akan searah dengan perubahan IHSG. Dari hasil output pengaruh Hang Seng dengan IHSG sudah sesuai dengan teori yang ada.

• c.    Pengaruh Kurs USD terhadap IHSG

Berdasarkan hasil estimasi dengan menggunakan TARCH (2,2), terlihat bahwa kurs USD memiliki pengaruh yang negatif dan signifikan terhadap     IHSG. Hal ini berarti

peningkatan kurs USD (dalam hal ini Rupiah mengalami epresiasi) akan menyebabkan IHSG melemah. Hal ini dimungkinkan oleh adanya pengalihan investasi dari pasar modal ke pasar valas, karena investor berusaha mendapatkan return yang lebih besar di pasar valas (Gede, 2006). Selain itu naiknya nilai kurs US$ menjadi sinyal negatif bagi pasar modal, hal ini dikarenakan melemahnya Rupiah menyebabkan gairah investasi menurun karena investor lebih suka menanamkan modalnya ke luar negeri. Hasil ini konsisten dengan penelitian Murwaningsari(2008) yang dapat membuktikan bahwa kurs USD berpengaruh negatif secara signifikan terhadap IHSG.

Prediksi IHSG Model ARCH/ GARCH

Berdasarkan pada model terbaik yang terbentuk yaitu TARCH (2,2), dilakukan prediksi terhadap IHSG untuk tanggal 3 Januari 2011. Hasil yang diperoleh adalah sebagai berikut: IHSGt=3578.67 + 77.13* VOL_ SAHAM + 0.03*HANGSENG -0.35*KURS

IHSGt = 3578.67 + 77.13 (21.36) + 0.03(22999.34)-0.35(8978) = 3578.67 + 1668.32 + 689.98 - 3142.3 = 2794,67

Berdasarkan hasil Prediksi menggunakan model TARCH (2,2) diperoleh nilai taksiran IHSG tanggal 3 Januari 2011     sebesar 2794,67.

Sedangkan data faktual adalah sebesar 3727,52 dengan selisih sebesar 932,85.

Prediksi IHSG model ARIMA

Berdasarkan model Arima (1,1,2), maka persamaan yang terbentuk untuk

meramalkan IHSGt adalah sebagai berikut :

γ_t=(1+Pl )δ+(1+Pi )Y_t-ι ^- PlY_t-2 + θlC_t-l + θ₂ε_t-2

Diketahui :

Pl = AR (1) = -0,9626

θl = MA (1) = 1,0639

θ₂ = MA (2) = 0,0882

δ = C ⁼ = 1,⁽44⁾55  ^,

Y_t = (1 - (-0,9626))1,4455 +(1-0,9626)Y_t-I - (-0,9626)Y_t-2 + 1,0639e_t-ι + 0,0882e_t-2

Y_t = (1 - (-0,9626))1,4455 +(1-0,9626)Y_t-ι - (-0,9626)Y_t-2 + 1,0639e_t-ι + 0,0882ε_t-2

Y_t = 2,8369 + 0,0374 Y_t-ι + 0,9626 Y_t-2 + 1,0639^_t-l + 0,0882ε_t-2

Nilai Prediksi IHSG 29 Desember 2010 :

Y_t

= 2,8369

+ 0,0374(IHSG 28 Des 2010)

+ 0,9626(IHSG 27 Des 2010)

Y_t = 2,8369 + 0,0374(3625,27)

+ 0,9626(3611,53)

Y_t = 2,8369 + 135,5851 + 3476,4587

Y_t = 3614,8807

Nilai Prediksi IHSG 30 Desember 2010 :

Y_t

= 2,8369

+ 0,0374(IHSG 29 Des 2010)

+ 0,9626(IHSG 28 Des 2010)

Y_t = 2,8369 + 0,0374(3659,99)

+ 0,9626(3625,27)

Y_t = 2,8369 + 136,8836 + 3489,6849

Y_t = 3629,4054

Selanjutnya kita mencari nilai residual pada peramalan yang akan kita lakukan : Nilai Residual 29 Desember 2010

= Y faktual - Y prediksi

= 3659,99 - 3614,88

= 45,11

Nilai Residual 30 Desember 2010 = Y faktual – Y Prediksi = 3699,22 – 3629,41 = 69,81

Setelah Nilai residual sudah dapat ditentukan, langkah selanjutnya adalah melakukan peramalan IHSG 03 Januari 2011 :

Y_t = 2,8369 + 0,0374 ^γt-ι

+ 0,9626 ^Yt-2

+ 1,0639^t-l

+ 0,0882e_t-2

^γ_t = 2,8369 + 0,0374V(30 Des 2010)

+ 0,9626V(29 Des 2010)

+ 1,0639e(30 Des 2010)

+ 0,0882e(29 Des 2010)

Y_t = 2,8369 + 0,0374(3699,22)

+ 0,9626(3659,99)

+ 1,0639(69,81)

+ 0,0882(45,11)

Y_t = 2,8369 + 138,3508 + 3523,1063 + 74,2708 + 3,9787

Y_t = 3742,54

Berdasarkan pada hasil prediksi, nilai taksiran untuk IHSG 3 Januari 2011 adalah sebesar 3742,54 sedangkan data faktualnya sebesar 3727,52 dengan selisih sebesar 15,02.

Berdasarkan analisis menggunakan model TARCH(2,2) maka diperoleh hasil sebagai berikut :

• a.    Variabel kurs USD-Rp berpengaruh negatif dan signifikan terhadap IHSG.

• b.    Volume Saham Berpengaruh positif dan signifikan terhadap IHSG.

• c.    Indeks Hang Seng berpengaruh positif dan signifikan terhadap IHSG,

Selanjutnya berdasarkan hasil prediksi     menggunakan     model

TARCH(2,2) dan ARIMA(1,1,2) maka diperoleh hasil sebagai berikut :

• a.    Model TARCH(2,2) memperoleh nilai taksiran IHSG tanggal 3 Januari 2011 sebesar 2794,67. Sedangkan data faktual adalah sebesar 3727,52 dengan selisih sebesar 932,85

• b.    Model ARIMA(1,1,2) memperoleh nilai taksiran untuk IHSG 3 Januari 2011 adalah sebesar 3742,54 sedangkan data faktualnya sebesar 3727,52 dengan selisih sebesar 15,02

KESIMPULAN DAN SARAN

Pada pemodelan TARCH(2,2) dapat dibuktikan bahwa volume perdagangan saham berpengaruh positif dan signifikan terhadap IHSG. Dengan demikian saat volume perdagangan saham mengalami peningkatan, maka IHSG juga akan mengalami peningkatan yang akan diikuti dengan meningkatnya nilai pasar dan pada akhirnya meningkat kan kesejahteraan investor. Begitupun sebaliknya saat volume perdagangan saham mengalami penurunan, maka IHSG juga akan mengalami penurunan yang akan diikuti dengan menurunnya nilai pasar dan pada akhirnya kesejahteraan investor akan menurun yang dapat menyebabkan investor akan memilih untuk berinvestasi di luar saham.

Indeks Hang Seng berpengaruh positif dan signifikan terhadap IHSG. Dengan demikian saat indeks Hang Seng mengalami peningkatan, maka IHSG juga akan mengalami peningkatan. Dengan demikian nilai perdagangan antara Indonesia dengan China akan mengalami peningkatan, investasi China di Indonesia juga akan meningkat. Begitu juga sebaliknya saat indeks Hang Seng mengalami penurunan, investasi China di Indonesia akan berkurang. Dapat pula dinyatakan bursa yang berkapitalisasi besar (kuat) mempengaruhi bursa yang berkapitalisasi rendah (lemah).

Kurs USD-Rp berpengaruh negatif dan signifikan terhadap IHSG. Saat kurs USD terhadap rupiah meningkat maka IHSG akan mengalami penurunan. Pada saat kurs USD terhadap rupiah meningkat investor akan cenderung berinvestasi dalam bentuk mata uang asing. Begitupun sebaliknya, saat kurs USD terhadap Rupiah mengalami penurunan maka IHSG akan meningkat. Pada saat kurs USD terhadap Rupiah menurun investor akan cenderung berinvestasi dalam bentuk saham. Sehingga dengan demikian pengaruh Volume perdagangan saham, Indeks Hang Seng dan Kurs USD-Rp terhadap IHSG masih sesuai dengan teori. Jika dilihat dari koefisien varian errornya semua menunjukkan hasil yang signifikan. Hal ini disebabkan R squared yang besar.

Berdasarkan hasil prediksi yang diperoleh dari model GARCH dan ARIMA, terlihat bahwa model ARIMA memberikan hasil selisih nilai terkecil antara faktual dan prediksi dibandingkan dengan model (GARCH). Sehingga dapat disimpulkan bahwa model ARIMA berbeda dengan GARCH, dan untuk data yang dihadapi saat ini, metode ARIMA dapat digunakan untuk memprediksi pergerakan IHSG karena mempunyai kesalahan lebih kecil.

Saran

Bagi peneliti berikutnya disarankan untuk menggunakan model ARCH-GARCH dengan menambah pengaruh bursa dunia lainnya. Hal tersebut dikarenakan negara yang perekonomiannya kuat akan mempengaruhi negara yang perekonomiannya lebih lemah atau bursa yang kuat akan mendominasi bursa yang lebih lemah.

REFERENSI

Djalal N, Nachrowi, dan Hardius Usman.

2006. Pendekatan Populer dan Praktis Ekonometrika untuk Analisis Ekonomi dan Keuangan. Fakultas Ekonomi Univertas Indonesia. Jakarta.

Djalal N, Nachrowi, dan Hardius Usman. 2007.Prediksi   IHSG Dengan

Model GARCH dan Model ARIMA. Jurnal Ekonomi dan Pembangunan Indonesia.

Adam, Latif, “ACFTA Dalam Perspektif Hubungan Dagang Indonesia China”,

http://inspirasitabloid.wordpress.com/201 0/03/19/acfta-dalamperspektif-hubungan-dagang-indonesia-china/, diakses tanggal 30 Mei 2012

Murwaningsari, Etty. 2008. Pengaruh Volume Perdagangan Saham, Deposito, dan Kurs Terhadap IHSG, Beserta Prediksi IHSG (Model GARCH dan ARIMA). Jurnal Ekonomi dan Bisnis Indonesia.

Widarjono, Agus.2005. Ekonometrika, Teori dan Aplikasi. Ekonosia. Yogyakarta.

Worldbank (2012). Indicator financial sector.

http://data.worldbank.org/indicator

Bank Indonesia (2012). Moneter.

http://www.bi.go.id/web/id/Monet er/Kurs+Bank+Indonesia/Kurs+Tr ansaksi/

finance.yahoo.com

Vol. 7, No. 2, Juli 2012

AUDI

Jurnal Akuntansi & Bisnis

192