Penggunaan Metode Orthogonal GARCH untuk Meramalkan Matriks Kovarians Return Indeks Harga Saham Sektoral Di Bursa Efek Indonesia

pISSN : 2301 - 8968

eISSN : 2303 - 0186

JEKT ♦ 12 [2] : 167-174

Penggunaan Metode Orthogonal Garch Untuk Meramalkan Matriks Kovarians Return Indeks Harga Saham Sektoral Di Bursa Efek Indonesia

Robiyanto Robiyanto

Fakultas Ekonomika dan Bisnis

Universitas Kristen Satya Wacana Salatiga 50711, Indonesia

ABSTRAK

Penelitian ini melakukan kajian kesamaan risiko pada indeks-indeks harga saham sektoral yang terdapat di Bursa Efek Indonesia dengan menggunakan metode Orthogonal Generalized Autoregressive Conditional Heteroscedasticity (Orthogonal GARCH). Data yang dipergunakan dalam penelitian ini adalah data seluruh indeks harga saham sektoral penutupan harian di Bursa Efek Indonesia yang terdiri dari sepuluh indeks harga saham sektoral selama periode 4 Januari 2011 hingga 17 Juli 2017. Dari sepuluh indeks harga saham sektoral yang dikaji ternyata terdapat dua komponen utama faktor yang mempengaruhi conditional variancenya. Hasil penelitian ini adalah bahwa indeks harga saham sektor pertanian dan pertambangan memiliki faktor risiko yang sama, sedangkan indeks harga saham sektoral lainnya memiliki faktor risiko yang sama. Temuan ini berimplikasi bahwa para manajer investasi harus membedakan faktor risiko saham-saham sektor pertanian dan pertambangan dari sektor lainnya.

Kata kunci: Orthogonal GARCH; Bursa Efek Indonesia; Value-at-Risk (VaR); Indeks harga saham sektoral; matriks kovarians

Klasifikasi JEL: C58; G11.

Use of the Orthogonal Garch Method to Predict the Covariance Return Matrix of the Sectoral Stock Price Index on the Indonesia Stock Exchange

ABSTRACT

This study conducted a risk communality assessment on sectoral stock price indices in Indonesia Stock Exchange by using Orthogonal Generalized Autoregressive Conditional Heteroscedasticity (Orthogonal GARCH) method. Data used in this research is daily closing of sectoral stock price indices at Indonesia Stock Exchange which consisting of 10 sectoral price indices. Research period are during January 4, 2011 until July 17, 2017. Of 10 sectoral stock price indices which studied apparently there are two principal component influencing its conditional variance. The result of this research is that stock index of agriculture and mining sector have the same risk factor, while other sectoral stock price indices have the same risk factor. These findings imply that investment managers must differentiate risk factors for agricultural and mining sectors from other sectors.

Keywords: Orthogonal GARCH; Indonesia Stock Exchange; Value-at-Risk (VaR); Sectoral stock price indices; Covariance matrix

JEL classification: C58; G11.

PENDAHULUAN

Teori Portofolio Modern diperkenalkan pertama kalinya oleh Markowitz (1952), dalam teori ini dinyatakan bahwa aset yang berkorelasi satu sama lain tidak akan memberikan manfaat diversifikasi yang efektif. Markowitz (1952) juga mengembangkan Mean-Variance Model untuk merumuskan portofolio. Sehingga varians sama halnya dengan korelasi merupakan input yang

Email : robiyanto.robiyanto@uksw.edu

sangat penting dalam pembentukan portofolio. Dalam manajemen investasi dan portofolio terutama bidang yang sangat terkait dengan manajemen risiko, melakukan permodelan dari sejumlah besar aset dari sisi varians dan kovariansnya merupakan hal yang sangat penting (Weide 2002). Lam et al. (2009) juga mengemukakan hal senada dengan menyatakan bahwa dalam portofolio dan manajemen risiko, kegiatan untuk mengestimasi

167

dan memperkirakan volatilitas dan korelasi return aset memainkan peranan yang penting, sehingga tidaklah mengherankan apabila minat dalam mengestimasi matriks kovarians dari portofolio yang memiliki ukuran yang sangat besar makin meningkat. Bai (2011) dan Alexander (2001a) menyebutkan bahwa kovarians matriks dari aset-aset dalam suatu portofolio akan cenderung memiliki korelasi yang kuat dengan risiko portofolio, akibatnya amatlah penting untuk mampu membuat matrik kovarians yang berskala besar dan semi definit positif dalam manajemen risiko.

Dalam kenyataannya, pembuatan matriks kovarians berskala besar dan semi definit positif tersebut tidaklah mudah dilakukan dan seringkali menjadi suatu tantangan bagi para pelaku dan akademisi dalam dunia manajemen investasi. Sehingga para pelaku di bidang finansial ini cenderung menggunakan penggunaan model faktor risiko untuk mensiasatinya walaupun dirasa sudah tidak memadai untuk melakukan penilaian portofolionya (Alexander 2001a). Model yang seringkali dipergunakan adalah model Generalized Autoregressive Conditional Heteroscedasticity (GARCH). Spesifikasi multivariat GARCH biasanya dilakukan dengan pertimbangkan kemudahan dalam membuatnya (Burns 2005), namun hal ini seringkali memberikan dampak pada hilangnya perhitungan-perhitungan umum yang diperlukan (Weide 2002).

Seiring dengan berjalannya waktu dan berkembangnya ilmu pengetahuan, para ahli matematika, statistik dan ekonometrika berupaya mengembangkan suatu alat yang mampu mengatasi kelemahan-kelemahan pada GARCH. Orthogonal GARCH sebagai salah satu cara baru dalam metode ARCH, dipandang sebagai suatu alat untuk mengatasi masalah-masalah yang timbul dalam permodelan multivariat GARCH. Orthogonal GARCH mudah untuk dipergunakan dan tidak membutuhkan batasan-batasan dalam model (Iqbal 2013). Orthogonal GARCH dikembangkan oleh Alexander (2001b). Dalam perkembangannya, aplikasi Orthogonal GARCH ini makin luas dan dapat digunakan untuk menghitung value-at-risk (VaR) (Holton 2014). Iqbal (2013) berpendapat bahwa Orthogonal GARCH mampu memperkirakan estimator yang robust dalam menghitung korelasi dan value-at-risk (VaR), bahkan akurat (Laurent et al. 2010).

VaR model merupakan model yang telah banyak digunakan oleh para pelaku dan akademisi di bidang manajemen investasi dan portofolio sebagai alat pengukuran risiko kuantitatif (Simons 1996). Pada kenyataannya, penggunaan Orthogonal GARCH dalam VaR ini acapkali terkait dengan risiko pasar, volatilitas pasar saham (Bai 2011) dan strategi portofolio baik aktif maupun pasif (Luo 2015).

Beberapa penelitian yang telah menggunakan metode Orthogonal GARCH dalam bidang manajemen investasi dan portofolio adalah Byström (2004); Lam et al. (2009); Bai (2011); Torres (2013). Byström (2004) mengkaji penggunaan Orthogonal GARCH dalam memperkirakan matriks kovarians dari indeks saham di kawasan Eropa Utara dan Atlantik Utara (negara-negara Nordic) selama periode dengan tingkat volatilitas yang tinggi pada tahun 19971998. Byström (2004) menemukan bahwa metode Orthogonal GARCH dapat diandalkan dan memiliki kinerja yang lebih baik dibandingkan metode perhitungan varians tradisional. Sedangkan Lam et al. (2009) menggunakan Orthogonal GARCH untuk menghitung matriks kovarians dengan melakukan kajian yang menggunakan sampel berjumlah besar yaitu sebanyak 63 aset yang meliputi saham, obligasi, dan mata uang. Dalam penelitian ini, Lam et al. (2009) menemukan bahwa model Orthogonal GARCH secara konsisten memiliki kinerja yang lebih baik dalam memprediksi matriks kovarians.

Bai (2011) melakukan penelitian mengenai kesamaan risiko dari saham-saham sektor energi seperti Exxon Mobil, Shell, Chevron, BP dan Conoco Phillips yang dipandang memiliki tingkat korelasi yang sangat tinggi. Penelitian Bai (2011) mampu memberikan bukti empiris bahwa metode Orthogonal GARCH mampu mereduksi tingkat kerumitan perhitungan, lebih lanjut Orthogonal GARCH juga mampu menghitung volatilitas dan korelasi dari semua aset bahkan mengendalikan residual yang disebut dengan noise sepanjang aset-aset yang ada memiliki korelasi yang tinggi. Sementara itu Torres (2013) menyimpulkan bahwa penggunaan Orthogonal GARCH sangat berguna dalam manajemen portofolio yang aktif dan paling tepat untuk digunakan dalam proses investasi.

Dari berbagai penjelasan di atas maka dapat dilihat bahwa metode Orthogonal GARCH merupakan metode yang handal dan dapat digunakan untuk proses penyederhanaan dalam

melihat kesamaan risiko pada berbagai aset sekaligus guna menciptakan matriks kovarians. Sayangnya metode ini jarang digunakan pada penelitian-penelitian di bidang investasi di Indonesia. Oleh sebab itu penelitian ini berupaya mengaplikasikan metode Orthogonal GARCH pada penilaian risiko indeks-indeks harga saham sektoral di Bursa Efek Indonesia yang berjumlah sepuluh indeks harga saham yaitu Indeks Harga Saham Sektor Pertanian, Indeks Harga Saham Sektor Industri Dasar, Indeks Harga Saham Sektor Industri Konsumsi, Indeks Harga Saham Sektor Keuangan, Indeks Harga Saham Sektor Infrastruktur, Indeks Harga Saham Sektor Industri Manufaktur, Indeks Harga Saham Sektor Pertambangan, Indeks Harga Saham Sektor Aneka Industri, Indeks Harga Saham Sektor Properti dan Indeks Harga Saham Sektor Perdagangan. Hal ini dilakukan karena sangat dimungkinkan bahwa sepuluh indeks harga saham sektoral tersebut cenderung memiliki faktor risiko yang sama, sama halnya dengan risiko khusus pada masing-masing indeks harga saham sektoral. Dengan melakukan kajian pada indeks harga saham sektoral ini maka dapat diketahui derajat faktor risiko yang sama yang menjadi penggerak utama indeks harga saham sektoral tersebut secara simultan. Hal ini penting dilakukan agar para investor ataupun manajer investasi dapat melakukan pemilihan sektor yang tepat dalam pembentukan portofolionya.

Berdasarkan hal ini maka pertanyaan penelitian (research question) yang diajukan adalah apakah indeks-indeks harga saham sektoral di Bursa Efek Indonesia memiliki faktor kesamaan risiko? Lebih lanjut dalam penelitian ini pendekatan orthogonal dilakukan dengan menggunakan GARCH dan kemudian dilanjutkan dengan Principal Component Analysis (PCA) sebagai solusi masalah dimensionalitas.

Orthogonal Generalized Autoregressive Conditional Heteroscedasticity (Orthogonal GARCH)

Metode Orthogonal GARCH sangat tergantung pada penggunaan Principal Component Analysis (PCA) dalam menyederhanakan faktor-faktor yang diperkirakan mampu menjelaskan berbagai variasi-variasi pada suatu data runtut waktu dan selanjutnya memanfaatkan matriks kovarians PCA tersebut guna disesuaikan dengan matriks kovarians data awal. Metode Orthogonal GARCH dipandang tepat untuk digunakan dalam

mengatasi masalah-masalah dalam praktek-praktek di bidang manajemen investasi dan portofolio karena mampu mengurangi dimensi-dimensi dari matriks kovarians yang harus diperkirakan (Bai 2011; Luo 2015; Robiyanto 2017). Luo (2015) mengemukakan bahwa dalam model Orthogonal GARCH, data runtut waktu yang diamati secara linier diubah agar dapat menjadi suatu rangkaian data runtut waktu yang independen dengan menggunakan PCA. Model Orthogonal GARCH yang diperkenalkan oleh Alexander (2001b) adalah sebagai berikut (disesuaikan dengan data yang dipergunakan dalam penelitian ini yang menggunakan data harian) :

Jika Yt adalah suatu data runtut waktu multivariat return harian dengan rata-rata nol pada k aset dengan panjang T dengan kolom yt,..., yk. Sehingga matriks Xt T X K dengan kolom xt,..., xk dapat dirumuskan dengan persamaan:

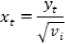
Dimana                    dengan adalah

varians sampel dari kolom ith Y_t.

Jika L menunjukkan matriks eigenvector korelasi populasi x_t dan l_m = (l_1,m,...,l_k,m) merupakan kolom mth. l_m adalah eigenvector k X 1 berhubungan dengan eigenvalue λ_m. Kolom L tersebut telah dipilih sehingga λ₁ > λ₂ > ... > λ_k.

Jika D adalah matriks eigenvalue diagonal, maka komponen utama mth dari sistem tersebut dapat dinyatakan sebagai:

p_m = x₁l_1,m + x₂l_2,m + ... + x_kl_k,m

Jika setiap vektor komponen utama p_m ditempatkan sebagai kolom pada matriks P T X k, sehingga           P = XL

Jika kolom komponen utama dimodelkan oleh GARCH (1,1) sebagaimana dianjurkan oleh Bollerslev (1986) dan Engle et al. (1987) sebagai berikut :            p_t | ψ_t-1 ~ N (0, Σ_t)

^pi,t ^{= ϵ}i,t σ_j^ = ω_i + α_i⅛-₁ ~ β_irf_t-₁

dimana Σ_t adalah matriks diagonal dari varians kondisional komponen utama P. ψ_t-1 yang berisi semua informasi yang tersedia hingga t-1. Matriks varians kondisional X_n adalah D_t = L Σ_t sehingga matriks kondisional kovarians Y adalah

H_t = rfVD_trfv

Model Estimasi dalam Metode Orthogonal GARCH

Jika Y menjadi matriks T X k dari return

harian k aset pada T hari. Maka return harian tersebut dapat diperoleh dengan menggunakan logaritma natural dari harga penutupan hari berikutnya dibagi dengan harga penutupan harian. Rumusnya adalah sebagai berikut (Alexander 2001; Torres 2013):

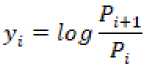
Dimana P_i adalah harga penutupan harian pada periode i.

Langkah pertama :

Menstandarisasi data ke dalam matriks X T X k dengan varians yang diestimasi dan rata-rata untuk setiap y_i dan memperoleh matriks korelasi XX^’.

Langkah kedua :

Melakukan analisis komponen utama (PCA) pada XX^’ untuk memperoleh vektor eigenvalue dan eigenvalue. Matriks eigenvektor ini dinotasikan dengan L dan kolom mth nya dengan l_m = (l_1,m,...,l_k,m), eigenvektor K X 1 berhubungan dengan eigenvalue λ_m. Sehingga kolom ini menjadi sehingga λ₁ > λ₂ > ... > λ_k..

Langkah ketiga :

Menentukan berapa banyak komponen utama yang harus digunakan. Jika komponen utama yang pertama dipilih, maka komponen utama mth dari sistem tersebut adalah

p_m = x₁l_1,m + x₂l_2,m + ... + x_kl_k,m

Dimana x_i adalah kolom ith dari kolom X_n, matriks TXn kemudian diekstrak dari X. Sehingga matriks komponen utama P ditunjukkan oleh matriks T X n dan diperoleh P = X_nW_n.

Langkah keempat :

Varians kondisional dari komponen utama ith p_i, i = 1, N diestimasi dengan menggunakan GARCH (1,1) :

p = ϵ i,t i,t

+ ^αi⅛-l +Pi^σ⅛

2

∑_r = diag(σ‰,... σ‰

Langkah kelima :

Matriks kovarians kondisional X_n adalah D_t = ¾2_t< dan matriks varians kondisional Y adalah

H_t = >∕VD_ty∕v

Dimana W_n = L_ndiag(Jλ_l,...,_y[λ^_n

Akurasi matriks kovarians kondisional V_t dari return orisinil ditentukan oleh seberapa banyak komponen n dipilih untuk mewakili sistem yang ada.

Data

Data yang dipergunakan dalam penelitian ini adalah data indeks harga saham sektoral penutupan harian periode 4 Januari 2011 hingga 17 Juli 2017 di Bursa Efek Indonesia. Indeks harga saham sektoral ini adalah Indeks Harga Saham Sektor Pertanian, Indeks Harga Saham Sektor Industri Dasar, Indeks Harga Saham Sektor Industri Konsumsi, Indeks Harga Saham Sektor Keuangan, Indeks Harga Saham Sektor Infrastruktur, Indeks Harga Saham Sektor Industri Manufaktur, Indeks Harga Saham Sektor Pertambangan, Indeks Harga Saham Sektor Aneka Industri, Indeks Harga Saham Sektor Properti dan Indeks Harga Saham Sektor Perdagangan. Keseluruhan data ini diperoleh dari Bloomberg.

HASILANALISIS DATA DAN PEMBAHASAN

Sebagaimana telah disampaikan pada bagian sebelumnya, metode Orthogonal GARCH menggunakan komponen utama yang dimodelkan oleh GARCH (1,1) dan mengkombinasikan dengan PCA. Metode ini akan mampu menghasilkan komponen-komponen utama yang dibentuk dari varians GARCH dari indeks-indeks harga saham sektoral, sehingga dari sepuluh indeks harga saham sektoral yang ada, maka akan terbentuk komponen-komponen utama yang memiliki faktor penggerak yang sama. Hal ini juga telah dilakukan oleh Lanne dan Saikkonen (2007) pada nilai tukar berbagai mata uang asing dan Park (2013) dalm mengkaji integrasi pasar modal di Asia.

Menurut Bai (2011) metode Orthogonal GARCH mampu diterapkan dengan baik pada suatu sistem data yang saling korelasi dengan tingkat korelasi yang tinggi. Oleh sebab itu dilakukan analisis korelasi return indeks harga saham sektoral dikaji dalam penelitian ini. Pada Tabel 1. dapat dilihat hasil analisis korelasi antar return Indeks Harga Saham Sektoral di Bursa Efek Indonesia. Berdasarkan Tabel 1. maka dapat dilihat bahwa semua indeks harga saham sektoral yang dikaji memiliki korelasi yang signifikan dan secara umum memiliki koefisien korelasi lebih dari 0,5.

Sementara itu, berdasarkan analisis data yang dilakukan dengan menggunakan metode Orthogonal GARCH yang melibatkan analisis GARCH dan PCA untuk return maka diperoleh hasil bahwa 2 komponen utama yang dapat menjelaskan varians dalam return Indeks Harga Saham Sektoral yang dikaji. Secara detail hal ini

Tabel 1.

Korelasi Return Indeks Harga Saham Sektoral di Bursa Efek Indonesia

		Agriculture	Basic	Consumer	Finance	Infrastructure	Manufacture	Mining	Miscelleneous	Property	Trade
Agriculture	Pearson Correlation	1	0.4623	0.3719	0.4315	0.3904	0.4673	0.5502	0.3830	0.4456	0.4660
	Sig. (2-tailed)		0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Basic	Pearson Correlation	0.4623	1	0.6156	0.7309	0.6224	0.8291	0.5309	0.6018	0.6929	0.6416
	Sig. (2-tailed)	0.0000		0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Consumer	Pearson Correlation	0.3719	0.6156	1	0.6182	0.5719	0.8839	0.4302	0.5100	0.5620	0.5923
	Sig. (2-tailed)	0.0000	0.0000		0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Finance	Pearson Correlation	0.4315	0.7309	0.6182	1	0.6623	0.7629	0.5064	0.6238	0.7003	0.6590
	Sig. (2-tailed)	0.0000	0.0000	0.0000		0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Infrastructure	Pearson Correlation	0.3904	0.6224	0.5719	0.6623	1	0.6728	0.4663	0.5380	0.5790	0.5791
	Sig. (2-tailed)	0.0000	0.0000	0.0000	0.0000		0.0000	0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Manufacture	Pearson Correlation	0.4673	0.8291	0.8839	0.7629	0.6728	1	0.5280	0.8027	0.6954	0.7014
	Sig. (2-tailed)	0.0000	0.0000	0.0000	0.0000	0.0000		0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Mining	Pearson Correlation	0.5502	0.5309	0.4302	0.5064	0.4663	0.5280	1	0.4124	0.4883	0.5695
	Sig. (2-tailed)	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000		0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Miscelleneous	Pearson Correlation	0.3830	0.6018	0.5100	0.6238	0.5380	0.8027	0.4124	1	0.5483	0.5522
	Sig. (2-tailed)	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000		0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Property	Pearson Correlation	0.4456	0.6929	0.5620	0.7003	0.5790	0.6954	0.4883	0.5483	1	0.6735
	Sig. (2-tailed)	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000		0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593
Trade	Pearson Correlation	0.4660	0.6416	0.5923	0.6590	0.5791	0.7014	0.5695	0.5522	0.6735	1
	Sig. (2-tailed)	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
	N	1593	1593	1593	1593	1593	1593	1593	1593	1593	1593

Sumber : Bloomberg, diolah.

dapat dilihat pada Tabel 2. dan Tabel 3.

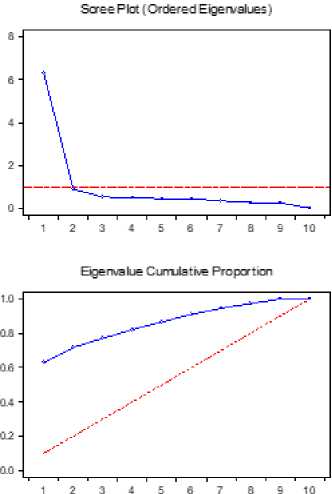
Berdasarkan Tabel 3. maka dapat diketahui bahwa delapan Indeks Harga Saham Sektoral yaitu Indeks Harga Saham Sektor Industri Dasar, Indeks Harga Saham Sektor Industri Konsumsi, Indeks Harga Saham Sektor Keuangan, Indeks Harga Saham Sektor Infrastruktur, Indeks Harga Saham Sektor Industri Manufaktur, Indeks Harga Saham Sektor Aneka Industri, Indeks Harga Saham Sektor Properti dan Indeks Harga Saham Sektor Perdagangan membentuk satu komponen utama (disebut dengan komponen utama pertama). Komponen utama pertama (PC1) memiliki eigenvalue sebesar 6,2964 dengan proporsi sebesar 0,6296 yang memiliki makna bahwa return delapan Indeks-Indeks Harga Saham Sektoral yang dikaji memiliki kesamaan penjelas varians return yang sama. Faktor pertama ini bahkan mampu menjelaskan 62,96% besarnya varians pada return Indeks-Indeks Harga Saham Sektoral yang dikaji. Ini menunjukkan bahwa delapan Indeks Harga Saham Sektoral tersebut memiliki satu faktor risiko utama yang sama dan menyumbang 62,96% besarnya conditional variance dari masing-masing

return Indeks-Indeks Harga Saham Sektoral tersebut.

Dua Indeks Harga Saham Sektoral yaitu Indeks Harga Saham Sektor Pertanian dan Indeks Harga Saham Pertambangan membentuk satu komponen utama (disebut dengan komponen utama kedua). Komponen utama kedua (PC2) memiliki eigenvalue sebesar 0,8822 dengan proporsi sebesar 0,0882. Faktor kedua ini mampu menjelaskan 8,82% besarnya varians pada return Indeks-Indeks Harga Saham Sektoral yang dikaji. Hal ini bermakna bahwa terdapat satu faktor risiko yang sama pada Indeks Harga Saham Sektor Pertanian dan Indeks Harga Saham Sektor Pertambangan, dan faktor risiko tersebut menyumbang 8,82% conditional variance dari masing-masing return Indeks-Indeks Harga Saham Sektoral yang dikaji. Indeks Harga Saham Sektor Pertanian dan Indeks Harga Saham Sektor Pertambangan dapat membentuk satu komponen utama karena keduanya terpengaruh oleh kondisi pasar komoditas internasional.

Saham-saham yang masuk ke dalam kedua indeks harga saham ini merupakan saham-saham penghasil komoditas (baik komoditas pertanian

Tabel 2. Hasil Analisis PCA (Gabungan)

Komponen	Eigenvalue	Nilai Kumulatif	Proporsi	Proporsi Kumulatif
1	6.2964	5.4143	0.6296	6.2964
2	0.8822	0.3504	0.0882	7.1786

Sumber : Bloomberg, diolah.

Tabel 3. Hasil Analisis PCA (Per Komponen Utama)

Variabel	PC 1	PC2
RESID_1_01 (Pertanian)	0.2412	0.6814
RESID_2_01 (Industri Dasar)	0.3425	-0.0753
RESID_3_01 (Konsumsi)	0.3139	-0.2652
RESID_4_01 (Keuangan)	0.3407	-0.1199
RESID_5_01 (Infrastruktur)	0.3076	-0.1103
RESID_6_01 (Manufaktur)	0.3739	-0.2408
RESID_7_01 (Pertambangan)	0.2702	0.5644
RESID_8_01 (Aneka Industri)	0.3031	-0.2200
RESID_9_01 (Properti)	0.3238	-0.0159
RESID_10_01 (Perdagangan)	0.3252	0.0886

Sumber : Bloomberg, diolah.

seperti minyak kelapa sawit (crude palm oil/ CPO), kakao, karet dan lain sebagainya; maupun komoditas pertambangan seperti logam mulia atau mineral lainnya yang sangat tergantung dengan harga komoditas yang dihasilkan di pasar internasional).

Kedua komponen utama ini mampu berkontribusi sebesar 71,786% dalam menjelaskan conditional variance return Indeks-Indeks Harga Saham Sektoral yang dikaji. Temuan ini juga menunjukkan bahwa metode Orthogonal GARCH mampu meringkas matriks kovarians menjadi lebih sederhana jika diterapkan lebih lanjut dapat memudahkan perhitungan portofolio. Hal ini konsisten dengan temuan penelitian Lam et al. (2009); Bai (2011); Luo (2015); Byström (2004).

Temuan ini menunjukkan bahwa para manajer investasi tidak dapat menyamaratakan faktor risiko bagi setiap indeks harga saham sektoral yang ada di Bursa Efek Indonesia. Hasil penelitian ini juga menunjukkan bahwa terdapat beberapa sektor-sektor yang memiliki faktor risiko yang relatif sama, namun juga terdapat sektor-sektor yang memiliki faktor risiko yang berbeda secara keseluruhan. Sehingga pembentukan portofolio saham dari lintas sektor di Bursa Efek Jakarta harus memperhatikan faktor risiko yang berbeda, karena jika melakukan pembentukan portofolio saham dari sektor-sektor dengan faktor risiko yang sama, maka manajer investasi tidak akan memperoleh manfaat diversifikasi. Penerapan Teori Modern Portofolio yang dikemukakan oleh Markowitz (1952) dapat

dilakukan karena sepanjang sektor-sektor yang ada memiliki faktor penggerak yang berbeda sehingga manfaat diversifikasi akan muncul. Penelitian ini juga membuktikan bahwa penggunaan Orthogonal GARCH dapat sangat bermanfaat bagi manajemen portofolio terutama dalam menghitung matriks kovarians.

Gambar 1. Eigenvalues

KESIMPULAN DAN SARAN

Hasil penelitian ini membuktikan bahwa metode Orthogonal GARCH mampu menyederhanakan matriks kovarians. Dari sepuluh indeks harga saham sektoral yang dikaji ternyata terdapat dua komponen utama faktor

yang mempengaruhi conditional variancenya. Hal ini tentu memiliki implikasi yang luas dalam perhitungan portofolio maupun dalam perhitungan VaR. Para manajer portofolio tidak perlu menghitung matriks kovarians secara luas melainkan dapat berfokus pada kedua komponen utama yang ditemukan memberikan kontribusi yang besar bagi conditional variance. Lebih lanjut penelitian ini menemukan bahwa Indeks Harga Saham Sektor Pertanian dan Indeks Harga Saham Sektor Pertambangan dipengaruhi oleh faktor risiko yang sama, sedangkan indeks-indeks harga saham sektoral lainnya dipengaruhi faktor risiko yang berbeda.

Hasil penelitian ini juga dapat digunakan untuk melakukan pembentukan portofolio. Manajer investasi disarankan tidak membentuk portofolio dari saham-saham yang berasal dari sektor yang dipengaruhi oleh faktor risiko yang sama, melainkan dari lintar sektor yang tidak memiliki faktor risiko yang sama. Para peneliti yang berminat mengembangkan penelitian yang sama dapat menggunakan data lintas negara yang lebih luas bahkan pada skala regional dan skala global agar dapat diketahui komponen utama yang berdampak pada pasar saham regional dan global.

REFERENSI

Alexander, C. 2001a. A Primer on the Orthogonal GARCH Model. Working Paper.

Alexander, C. O. 2001b. Orthogonal GARCH. In Mastering Risk, edited by C. O. Alexander. New York: Prentice–Hall, 21-38.

Bai, J. 2011. Using Orthogonal GARCH to Forecast Covariance Matrix of Stock Returns. Thesis, The Faculty of the Department of Economics, University of Houston, Houston.

Bollerslev, T. 1986. Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics 31:307-327.

Burns, P. 2005. Multivariate GARCH with Only Univariate Estimation. Working Paper.

Byström, H. N. E. 2004. Orthogonal GARCH and covariance matrix forecasting: The Nordic

stock markets during the Asian financial crisis 1997–1998 The European Journal of Finance 10 (4).

Engle, R. F., D. M. Lilien, dan R. P. Robins. 1987. Estimating Time Varying Risk Premia in the Term Structure: The Arch-M Model. Econometrica 55 (2):391-407.

Holton, G. A. 2014. Value at Risk: Theory and Practice. 2nd ed. Belmont, MA, United States: www.value-at-risk.net.

Iqbal, F. 2013. Robust Estimation for the Orthogonal GARCH Model. The Manchester School 81 (6):904-924.

Lam, L., L. Fung, dan I.-w. Yu. 2009. Forecasting a large dimensional covariance matrix of a portfolio of different asset classes. Hong Kong Monetary Authority Working Paper.

Lanne, M., dan P. Saikkonen. 2007. A Multivariate Generalized Orthogonal Factor GARCH Model. Journal of Business & Economic Statistics 25 (1):61-75.

Laurent, S., J. V. K. Rombouts, dan F. Violante. 2010. On the Forecasting Accuracy of Multivariate GARCH Models. Working Paper.

Luo, C. 2015. Stochastic Correlation and Portfolio Optimization by Multivariate GARCH. Dissertation, Graduate Department of Mathematics, University of Toronto, Toronto.

Markowitz, H. M. 1952. Portfolio Selection. Journal of Finance 7 (1):77-91.

Park, C.-Y. 2013. Asian Capital Market Integration: Theory and Evidence. ADB Economics Working Paper Series 351.

Robiyanto, R. 2017. The Analysis of Capital Market Integration in ASEAN Region by Using the OGARCH Approach. Jurnal Keuangan dan Perbankan 21 (2):169-175.

Simons, K. 1996. Value at Risk-New Approches to

Risk Management. New England Economic Review (September/October):3-13.

Torres, O. D. l. T. 2013. Orthogonal GARCH matrixes in the active portfolio management of defined benefit pension plans: A test for Michoacán. Economía: teoría y práctica 39.

Weide, R. v. d. 2002. GO-GARCH: a multivariate generalized Orthogonal GARCH model. Journal of Applied Econometrics 17 (5):549–564.

174