Peramalan Jumlah Kunjungan Wisatawan Mancanegara (Wisman) Ke Bali Tahun 2019: Metode ARIMA
on
JEKT ♦ 8 [2] : 136 - 141
ISSN : 2301 - 8968
Peramalan Jumlah Kunjungan Wisatawan Mancanegara Wisman) ke Bali Tahun 2019: Metode ARIMA
Rukini*)
Putu Simpen Arini
Esthisatari Nawangsih Badan Pusat Statistik Provinsi Bali
ABSTRAK
Pariwisata Indonesia telah berkembang secara signifikan selama beberapa tahun terakhir. Pada tahun 2013 sektor pariwisata Indonesia menyumbang devisa sebesar 10.054 juta US$., menduduki urutan ketiga komoditas ekspor Indonesia. Kementerian Pariwisata dan Ekonomi Kreatif menargetkan kunjungan wisatawan mancanegara wisman) ke Indonesia sebesar 20 juta wisman dengan target devisa sebesar 240 triliun rupiah tahun 2019. Selama ini sumbangan wisman Bali terhadap wisman nasional hampir mencapai 40 %. Bila dikaitkan dengan target nasional sebesar 20 juta wisman maka jumlah wisman yang datang ke Bali pada tahun 2019 sedikitnya harus mencapai 8 juta wisman. Dengan menggunakan metode ARIMA, ramalan jumlah kedatangan wisman di Bali 5,07 juta pada tahun 2019 jauh di bawah target. Hasil ini menunjukkan bahwa pemerintah harus memberikan lebih banyak usaha untuk mengembangkan pariwisata di tahun mendatang untuk memenuhi target.
Kata kunci: target wisman, ARIMA, peramalan
Tourits Forecasting To Bali in 2019: ARIMA Method
ABSTRACT
IndonesiaTourism has been growing significantly over the past few years. In 2013, income from tourism reached 10,054 millions dollars, occupied the third place of indonesia export commodities. The ministry of tourism and creatice economy has targeted 20 millions arrivals and 240 trillion rupiahs from international tourist arrivals in 2019. As Bali has been contributing for more than 40 percent of international tourist arrivals in Indonenesia, it is expected to have around 8 millions international arrivals in 2019. Using ARIMA method, it is predicted that the number of international tourist arrivals in Bali will be 5,07 millions in 2019, far below the target. This result suggests that government should give more effort to develop tourism in the upcoming years to fulfil the target.
Keywords : target tourists, ARIMA, forecasting
PENDAHULUAN
Sebagai salah satu negara berkembang, penopang perekonomian Indonesia salah satunya adalah sektor Pariwisata, dengan daya tarik terletak pada ragam wisata budaya dan keindahan wisata alam, serta berbagai masakan yang mengandung nilai cita rasa tinggi dalam wisata kulinernya. Daya tarik tersebut yang pada akhirnya membuat Indonesia dikenal sebagai salah satu negara tempat wisata yang populer.
Sektor pariwisata diharapkan dapat menggerakan ekonomi rakyat karena dianggap sektor yang paling siap dari segi fasilitas, sarana dan prasarana dibandingkan dengan sektor usaha lainnya. Harapan ini dituangkan dalam target devisa Indonesia pada tahun 2019 sebesar 240 triliun rupiah dan jumlah wisatawan mancanegara wisman) sebesar 20 juta wisman Republika, 26 Januari 2015)
Bali merupakan destinasi utama wisata di Indonesia. Bali merupakan salah satu surga wisata
Tabel 1. Karakteristik ACF dan PACF yang Stasioner
|
Proses |
ACF |
PACF |
|
Autoregressive orde p |
Dies down |
Cuts off setelah lag ke-p |
|
Moving Average orde q |
Cuts off setelah lag ke-q |
Dies down |
|
ARMA orde p,q) |
Dies down |
Dies down |
Sumber: Makridakis, 1999.
dunia dengan sejuta pesona keindahan alam dan kekayaan budaya yang dimilikinya. Dengan berbagai pesona tersebut, Bali mampu memikat wisatawan baik asing maupun domestik, sehingga mampu menjadi Bali adalah penyumbang utama terhadap jumlah wisman nasional. Pada tahun 2014, sumbangan wisman Bali terhadap wisman nasional mencapai 39,80%. Posisi berikutnya adalah Jakarta dan Batam dengan sumbangan masing-masing sebesar 24,13% dan 15,05%. Melihat tingginya andil Bali terhadap wisman nasional maka tidak bisa dipungkiri bahwa keberhasilan target wisman nasional sangat ditentukan oleh capaian wisman Bali pada tahun 2019. Jika sumbangan wisman Bali terhadap nasional sebesar 40 %, maka dengan target nasional sebesar 20 juta wisman maka jumlah wisman yang datang ke Bali pada tahun 2019 sedikitnya harus mencapai 8 juta wisman. Untuk mencapai target minimal ini, tentu tak lepas dari perencanaan promosi pariwisata yang baik. Data yang akurat dan uptodate diperlukan untuk menyusun strategi di bidang pariwisata. Untuk memperoleh gambaran capaian wisman maka diperlukan metode peramalan akan banyaknya jumlah wisman yang berkunjung di Bali pada tahun 2019.
Dengan demikian, peramalan jumlah wisman menjadi penting dan ketepatan akan analisis time series akan sangat bermanfaat bagi penetapan strategi peningkatan sektor pariwisata yang dapat menarik wisatawan untuk berkunjung ke Bali. Peramalan jumlah kunjungan wisman yang masuk ke suatu negara sangat dibutuhkan bagi pelaku bisnis pariwisata, sehingga memodelkan data jumlah kunjungan wisman perlu untuk dilakukan. Penelitian ini mencoba meramalkan jumlah wisman yang datang melalui Bandara Udara Ngurah Rai dan pelabuhan selama tahun 2014-2019.
Metode ARIMA Box-Jenkins. Prosedur pembentukan model ARIMA meliputi beberapa tahapan yaitu identifikasi, estimasi, cek diagnosa dan peramalan. Model Box-Jenkins (ARIMA) dibagi ke dalam 3 kelompok, yaitu: model autoregressive AR), moving average MA), dan model campuran ARMA autoregressive moving average) yang mempunyai karakteristik dari dua model pertama.
Namun sebelum melalui tahapan tersebut data harus stasioner yaitu data yang tidak mengalami pertumbuhan dan penurunan. Data yang stasioner merupakan syarat dari pembentukan model ARIMA baik stasioner dalam varian maupun dalam mean rata-rata). Jika data tidak stasioner dalam varian dapat dilakukan transpormasi pangkat power transformation), Box dan Cox dalam Wei (2006). Jika nilai P-value sama dengan 1 satu) berarti data tersebut sudah stasioner dalam varian. Sementara jika data tidak stasioner dalam mean, dapat dilakukan dengan cara pembedaan atau differencing
Makridakis, S., Weelwright, S.S., & V.E., 1999).
Identifikasi. Dalam mengidentifikasi model ARIMA (p, d, q) dapat dilakukan dengan melihat plot ACF (Autocorrelation fuction) dan plot PACF Parsial Autocorrelation fuction).
Bentuk model AR (Autoregressive) atau AR (p) atau model ARIMA (p, 0,0) adalah:
Zt = φ1Ζt-1 + φ2Ζt-2 + ... + φpZt-p + at........... 1) dimana:
φ (B) = (1 –φ B – ... –φ Bp) Z data deret waktu p 1 p t =
sebagai variabel respon pada waktu ke-t; Zt = data deret waktu sebagai variabel respon pada waktu <^ <^
ke-1 yang telah stasioner; Zt-ι,∙∙∙,Zt-p = data deret waktu ke t -1, ..., t - p . dan φ1, φ2,.... φp = parameterparameter autoregressive; at = nilai kesalahan pada waktu ke-t
Selanjutnya untuk model MA Moving Average) atau MA (q) atau model ARIMA (0,0, q) adalah:
Zt = a - θat-1 - θat-2 -l - θa .......(2)
-- q -q
dimana:
θq(B) = (1 - θ1 B -L - θ B); θ1,θ2,L θqadalah parameter-parameter moving average; at ,^, at-q adalah nilai kesalahan pada kurun waktu ke-t, t-1, … , t-q. Sementara model ARIMA yang merupakan gabungan dari model AR dan model MA serta melalui proses differencing adalah:
φp(B)(1 - B)dZt =θq (B)at..................................(3)
dimana: (1 - B)d adalah pembedaan (differencing) pada orde ke-d; dan B adalah backward shift BZt = Zt-i
Estimasi Parameter. Ada beberapa cara yang dapat digunakan untuk mendapatkan parameterparameter model ARIMA Wei, 2006), antara lain : i) Metode Momen; ii) Metode Maximum Likelihood; iii) Metode OLS Ordinary Least Squares). Secara umum, misalkan δ adalah suatu parameter pada model ARIMA mencakup φ , θ dan µ) dan δ adalah nilai estimasi dari parameter tersebut, serta s.e δ adalah standar error dari nilai taksiran δ maka
uji signifikansi parameter dapat dilakukan sebagai berikut:
Hipotesa:
Η0 : δ = 0(parameter tidak signifikan)
Η0 : δ ≠ 0 (parameter signifikan)
Statistik uji dilakukan dengan menggunakan rumus 4).
Statistik uji dilakukan dengan menggunakan rumus 4).
^
δ t=
s. e ((δ)
4)
Dimana daerah penolakan : Tolak H0 jika 111> ta /2-n-m atau menggunakan nilai p-value<α artinya parameter signifikan.
Pemeriksaan Diagnostik. Pemeriksaan diagnosis residual dari model, yaitu residual bersifat white noise yang berarti bahwa antara residual tidak ada lagi yang berkorelasi dan berdistribusi normal. Pengujian asumsi white noise menggunakan uji Ljung-Box dengan hipotesis sebagai berikut: H0:ρ1=ρ2=L =ρK =0 residual White Noise) H1 : minimal ada satu ρk ≠ 0 (residual tidak White
Noise),
Dengan k = 1,2,..., K Statistik Uji dihitung menggunakan rumus 5).
K
Q = n(n + 2)∑(n - k)-1 r’2 ................................(5)
k=1
dimana:
r k = ACF residual; k = banyaknya residual; dan k = lag ke-k. Daerah penolakan: Tolak Ho jika m = p + q, dengan m = p + q orde ARMA) atau dengan menggunakan p-value<a , artinya tidak memenuhi asumsi residual bersifat white noise. Pengujian selanjutnya yaitu uji asumsi residual berdistribusi normal. Pengujian ini dilakukan dengan menggunakan Kolmogorov Smirnov Daniel, 1989). Hipotesis yang digunakan adalah :
H0 : Fn (x) = F0l (x) atau residual berdistribusi normal H1 : Fn (x) ≠ F0 (x) atau residual tidak berdistribusi normal
Dengan statistik uji : D = sup | Fn (x) - F0 (x) | (2.3); dimana : F0 (x) = fungsi yang dihipotesiskan berdistribusi normal Fn (x) ; = fungsi distribusi kumulatif dari data asal; n = banyaknya residual; Nilai Dhitung dibandingkan dengan nilai n pada tabel Kolmogorov-Smirnov dengan derajat bebas n . Daerah penolakan: Tolak H jika atau 0 hitu~ng a n
dapat menggunakan p-value. Jika p-value < ho berarti H0 ditolak yang berarti residual tidak berdistribusi normal.
Pemilihan Model Terbaik. Untuk menentukan model terbaik dapat digunakan kriteria pemilihan model yang berdasarkan residual dan kesalahan peramalan Wei, 2006). Adapun kriteria pemilihan model yang berdasarkan residual pada data insample menggunakan nilai :
-
(1) Akaike Information Criteria (AIC).
AIC (M) = n ln σα2 + 2 M.................................(6)
dengan :na =banyaknya residual; M = jumlah parameter di dalam model; σˆa2= varians dari residual.
-
(ii) . Schwartz’s SBC
Kiteria Bayesian untuk pemilihan model terbaik Schwartz’s Bayesian Criterion), Schwartz (1978) di dalam wei (2006) didefinisikan sebagai berikut.
SBC (M) = n ln σ2 + M In n.........................(7)
DATA DAN METODOLOGI
Dalam penelitian ini, data yang digunakan adalah data sekunder yang diperoleh dari Badan Pusat Statistik Provinsi Bali, yakni jumlah kunjungan wisatawan mancanegara per bulan dari bandara internasional Ngurah Rai dan pelabuhan dengan series data dari Januari 2000 hingga Desember 2014. Pada proses analisis, data akan dibagi menjadi dua bagian yaitu data training untuk pembentukan model dan data testing untuk validasi dan pemilihan model terbaik. Data periode Januari 2000 sampai dengan Desember 2013 digunakan sebagai data training in-sample) dan data periode Januari 2014 sampai dengan Desember 2014 sebagai data testing out-sample).
Proses pembentukan model ARIMA yang meliputi tahapan identifikasi, estimasi parameter, cek diagnosa dan berdistribusi normal seperti telah diuraikan sebelumnya.
Gambar 1. Time Series Plot Jumlah Wisman
Tim e Series Plot of Wism a n
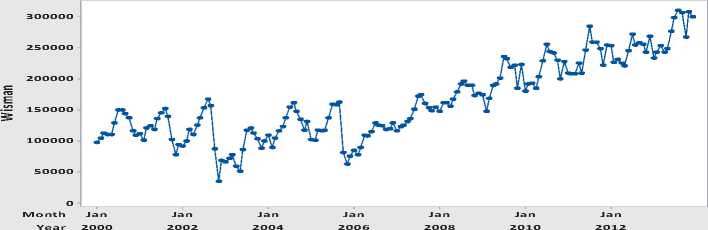
Sumber: hasil olah data, 2015.
Gambar 2. Box-Cox Transformation Jumlah Wis- Gambar 3. Plot ACF Jumlah Wisman
man.
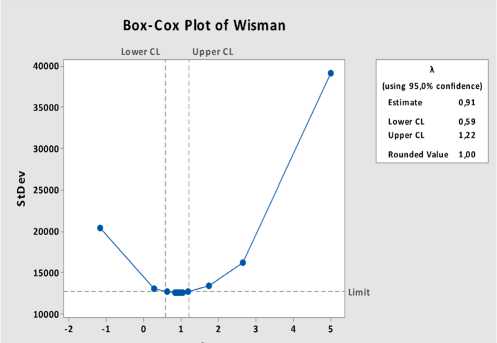
Sumber: hasil olah data, 2015.
Autocorrelation Function for Wisman (with 5% significance limits for the autocorrelations)
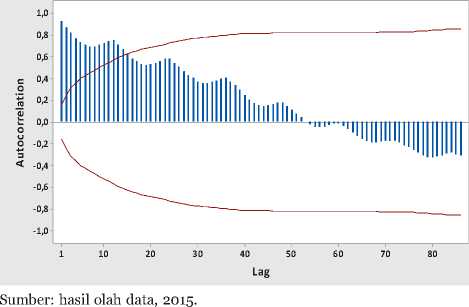
HASIL DAN PEMBAHASAN
Analisis ARIMA
Langkah awal dalam metode ARIMA adalah dengan membuat plot time series data, sebagaimana dapat dilihat pada Gambar 1.
Gambar 2. menunjukkan hasil Box-Cox Transformation dimana nilai rounded value = 1 hal ini mengindikasikan bahwa data jumlah wisman telah stasioner dalam varian, sedangkan Gambar 3. menunjukkan plot Autocorrelation Function (ACF) jumlah wisatawan mancanegara, terlihat pola dies down yang lambat dan berulang pada periode ke-12. Hal ini mengindikasikan bahwa databelum stasioner dalam mean rata-rata) dan adanya faktor musiman. Sehingga perlu dilakukan differencing 1 reguler kemudian di differencing kembali untuk musiman 12. Gambar 3. dan Gambar 4. menunjukkan plot ACF dan PACF data jumlah wisman setelah differencing 1 reguler dan differencing musiman 12. Setelah dilakukan proses differencing, plot ACF memperlihatkan bahwa data telah stasioner dalam rata-rata. Melalui plot ACF dan PACF tersebut dapat diidentifikasi order model ARIMA yang sesuai untuk data jumlah wisman.
Tabel 2. Hasil Identifikasi Dugaan Model ARIMA
|
Model |
Estimasi Parameter |
White Noise |
Berdis-tribusi Normal |
AIC |
|
ARIMA 0,1,1) 0,1,1)12 |
- |
3420,139 | ||
|
ARIMA 1,1,0) 1,1,0)12 |
- |
3456,995 |
Sumber: hasil olah data, 2015.
Dengan melihat pola PACF yang dies down dan ACF cut off di lag1 dan lag 12, maka dugaan model ARIMA yang terbentuk adalah model ARIMA (0,1,1)(0,1,1)12 dan ARIMA 1,1,0) 1,1,0)12. Untuk menetukan model ARIMA yang baik dari kedua model ARIMA tersebut adalah dengan melihat nilai AIC yang terkecil yaitu model ARIMA (0,1,1)(0,1,1)12 .Hasil identifikasi tersebut terlihat pada Tabel 2.
Untuk menangani asumsi kenormalan yang belum terpenuhi maka salah satu langkah penanganan adalah dengan mendeteksi adanya data outlier. Hasil identifikasi 5 data outlier pada model ARIMA 0,1,1) 0,1,1)12 dapat terlihat pada Tabel 3.
Dengan melakukan estimasi dan uji signifikansi parameter dengan data outlier, hanya ada 1 data outlier yang signifikan seperti terlihat pada Tabel 4.
Gambar 4. Plot ACF Jumlah Wisman setelah differencing 1 reguler dan musiman 12
Gambar 5. Plot PACF Jumlah Wisman setelah differencing 1 reguler dan musiman 12
Autocorrelation Function for Diff1_12 (with 5% significance limits for the autocorrelations)
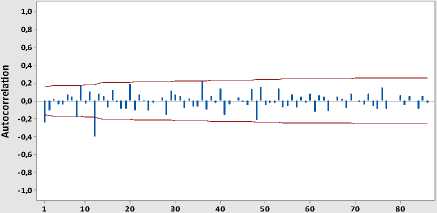
Lag
Sumber: hasil olah data, 2015.
Partial Autocorrelation Function for Diff1_12 (with 5% significance limits for the partial autocorrelations)
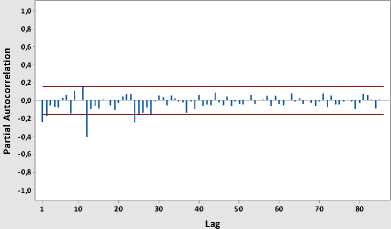
Sumber: hasil olah data, 2015.
Tabel 3. Hasil Identifikasi 5 data outlier pada model ARIMA 0,1,1) 0,1,1)12
|
Obs |
Type |
Estimate |
Square |
Chi-Sqrt |
|
70 |
Shift |
-60433,8 |
32,05 |
<,0001 |
|
34 |
Shift |
-63805,0 |
34,33 |
<,0001 |
|
167 |
Additive |
41211,3 |
18,55 |
<,0001 |
|
22 |
Shift |
-29391,0 |
8,22 |
0,0041 |
|
35 |
Additive |
-26280,3 |
9,91 |
0,0016 |
Sumber: hasil olah data, 2015.
Tabel 4. Estimasi dan Uji Signifikansi Parameter Model
ARIMA 0,1,1) 0,1,1)12 Jumlah Wisman dengan data outlier yang signifikan.
|
Parameter |
Estimasi |
p-value |
Lag |
Variabel Keputusan | |
|
θ1 |
0,37549 |
<,0001 |
1 |
y |
Signifikan |
|
θ12 |
0,76341 |
<,0001 |
12 |
y |
Signifikan |
|
ω1 |
-21642 |
0,0147 |
0 |
LS22 |
Signifikan |
Sumber: hasil olah data, 2015.
Dengan taraf signifikansi 5% memiliki nilai P-value kurang dari alpha 0,05 yang berarti parameter telah signifikan yang dapat dimasukkan ke dalam model ARIMA.
Berdasarkan pengujian residual model ARIMA 0,1,1) 0,1,1)12 Jumlah wisman dengan data outlier yang signifikan menunjukkan bahwa residual sudah whitenoise dengan nilai p-value yang lebih besar dari α = 0.05 . Sedangkan pengujian asumsi kenormalan dengan uji Kolmogorov-Smirnov dengan taraf signifikansi 5% memiliki nilai p-value lebih dari 0,05. Sehingga dapat disimpulkan bahwa residual sudah memenuhi asumsi berdistribusi normal, seperti terlihat pada Tabel 5.
Persamaan Model ARIMA 0,1,1) 0,1,1)12 Jumlah Wisman dengan data outlier yang signifikan adalah sebagai berikut :
Tabel 5. Hasil Uji White Noise Residual Model ARIMA 0,1,1) 0,1,1)12
|
Jumlah Wisman dengan data outlier yang signifikan | ||||
|
Lag |
Chi-Sqrt |
DF |
p-value |
Keputusan |
|
6 |
3,49 |
4 |
0,4794 |
White Noise |
|
12 |
7,78 |
10 |
0,6501 |
White Noise |
|
18 |
10,60 |
16 |
0,8337 |
White Noise |
|
24 |
13,62 |
22 |
0,9145 |
White Noise |
|
30 |
21,27 |
28 |
0,8139 |
White Noise |
Sumber: hasil olah data, 2015.
Tabel 6. Hasil uji normalitas residual Model ARIMA 0,1,1) 0,1,1)12
|
Jumlah Wisman dengan data outlier yang signifikan | |||
|
Test |
D_hitung |
p-value |
Keputusan |
|
Kolmogorov-Smirnov |
0,066202 |
0,0940 |
Berdistribusi Normal |
Sumber: hasil olah data, 2015.
Tabel 7. Hasil Ramalan Jumlah Wisman Provinsi Bali Tahun 2014 berdasarkan Model ARIMA
|
Tahun |
Ramalan |
Aktual |
Persentase Error |
|
2014 |
3.722.293 |
3.766.638 |
1,06 |
|
2015 |
3.992.851 | ||
|
2016 |
4.263.410 | ||
|
2017 |
4.533.968 | ||
|
2018 |
4.804.526 | ||
|
2019 |
5.075.084 |
Sumber: hasil olah data, 2015.
Xt =-21642LS22 + (1 - 0,37549B - 0,76341B12)at ...(8)
Dari hasil model ARIMA tersebut diatas menggambarkan bahwa jumlah wisman pada saat ke t ada kaitannya dengan data observasi ke 22 sebesar –21642 dan kesalahan pada saat ke t-1 sebesar 0,37549 dan kesalahan saat t-12 sebesar 0,76341.
Ramalan Jumlah Wisman yang Datang ke Bali Tahun 2014-2019
Hasil peramalan jumlah wisman berdasarkan model ARIMA untuk tahun 2014 sebesar 3.722.293 orang, sementara secara aktual jumlah wisman yang datang ke Bali tahun 2014 sebanyak 3.766.638 orang. Hasil ramalan tersebut menunjukkan hasil yang mendekati sebenarnya atau hanya terjadi kesalahan ramalan sebesar 1,06 %.
SIMPULAN
Berdasarkan hasil penelitian, dapat diambil kesimpulan bahwa jumlah kedatangan wisman Bali pada tahun 2019 hanya sebesar 5,07 juta wisman. Nilai ini jauh dari jumlah minimal yang harus di capai Bali yaitu sebesar 8 juta wisman. Untuk memenuhi target minimal ini maka diperlukan inovasi di bidang promosi pariwisata baik dari segi metode promosi maupun pengembangan produk pariwisata itu sendiri. Dalam lingkup nasional, diperlukan pengembangan destinasi wisata lain selain Bali, Jakarta, dan Batam untuk mendongkrak capaian target wisman nasional pada tahun 2019 sebesar 20 juta wisman.
REFERENSI
Badan Pusat Statistik Provinsi Bali, 2000-2014. Statistik Wisatawan Mancanegara ke Bali
Box, G.E., Jenkins, G., & Reinsel, G.C. (1994), Time Series Analysis:Forecasting and Control (3rd ed. ). New Jersey
Bowerman, B.L., & О’Connel, R.T. (1993),Forecasting and Time Series: An. Applied Approach.California:Duxbury Press.
Daniel 1989), Statistika Nonparametrik Terapan. Jakarta: PT. Gramedia
Makridakis, S., Weelwright, S.C., & McGee.,V.E (1999), Metode dan Aplikasi Peramalan. Edisi kedua jilid I penerbit Erlangga.
Republika, Senin 26 Januari 2015: Arif Yahya, Menteri Pariwisata RI: Kita akan Siapkan Wisata Khas
Wei, W. S. 2006. Time Analysis Univariate and Multivariate Methods, New York : Addison Wesley Publishing Company, Inc.
141
Discussion and feedback