Determining Crystallite Size Using Scherrer Formula, Williamson-Hull Plot, and Particle Size with SEM

(M. Sumadiyasa, I B. S. Manuaba)

Penentuan Ukuran Kristal Menggunakan Formula Scherrer, Williamson-Hull Plot, dan Ukuran Partikel dengan SEM

Determining Crystallite Size Using Scherrer Formula, Williamson-Hull Plot, and Particle Size with SEM

M. Sumadiyasa1, I B. S. Manuaba2

1, 2Department of Physics, Faculty of Mathematics and Natural Sciences, Udayana University Kampus Bukit Jimbaran, Badung, Bali Indonesia 80361

Abstrak – Telah ditentukan ukuran kristal dengan teknik XRD menggunakan persamaan Scherrer dan metode Williamson-Hull Plot. Ukuran partikel ditentukan dengan SEM menggunakan software Image-J. Untuk tujuan tersebut, telah disintesis sampel campuran fase Gd0,95La0.05Ba2Cu3O7-δ. Dari hasil perhitungan, diperoleh ukuran kristal dalam orde nanometer, akan tetapi, ukuran kristal yang dihasilkan dari persamaan Scherrer dan Scherrer Termodifikasi berbeda yaitu masing-masing 63,1675 nm dan 67,0005 nm. Hasil perhitungan ukuran kristal dengan persamaan Scherrer secara langgsung maupun termodifikasi sangat berbeda dengan hasil dari metode Williamson-Hull Plot (97,3040 nm). Sementara itu, hasil dari metode Williamson-Hull Plot dan SEM menunjukkan nilai yang hamper sama (98,7297nm).

Kata kunci: ukuran kristal, ukuran partikel, persamaan Scherrer, metode Williamson-Hull Plot, Scherrer Termodifikasi

Abstract – It has been determined the crystallite size by XRD technique using Scherrer equation and Williamson-Hull Plot method. While the particle size is determined by SEM using Image-J software. For this purpose, synthesized samples of compound Gd0,95La0.05Ba2Cu3O7-δ phase. From the calculation results, obtained the crystallite size in nanometers order, however the crystallite size resulting from the Scherrer equations and Scherrer Modified is different, i.e. 63.1675 nm and 67.0005 nm. The results of the crystallite size calculation by the scherrer equation directly and modified differed from that of the Williamson-Hull Plot method (97,3040 nm). Meanwhile, the results of the Williamson-Hull Plot methods and SEM show almost the same value (98.7297nm).

Key words: crystallite size, particle size, Scherrer equation, Williamson-Hull Plot methode, Modified Scherrer

  • I.    PENDAHULUAN

Nanopartikel menunjukkan sifat yang berbeda dengan sifat partikel tersebut jika dalam bentuk bulk [1]. Nanopartikel logam memiliki sifat fisika yang berbeda dari logam dalam bentuk bulk, misalnya memiliki titik leleh yang lebih rendah, luas permukaan spesifik yang lebih besar, serta sifat optik khusus. Meskipun material dalam skala bulk maupun nanopartikel terbuat dari atom yang sama, tetapi kedua material tersebut akan memperlihatkan warna koloid yang berbeda pada skala nano. Secara umum, ukuran nanopartikel adalah antara 1 - 100 nm [2]. Bagaimana partikel dalam skala nano dapat diukur?

Salah satu cara untuk mengukur partikel dalam orde nanometer adalah dengan teknik difraksi sinar-X. Teknik ini sering digunakan dalam penelitian, terutama untuk menentukan berbagai parameter fisika dari material seperti struktur kristal, strain, komposisi fase, struktur unit sel, cacat kristal dan ukuran kristal, bahkan susunan atom-atom di dalam material amorf seperti polimer. Dalam teknik

difraksi sinar-X sering menggunakan sampel dalam bentuk bubuk terutama dalam mengkarakterisasi struktur kristalografi, ukuran kristal (ukuran butir) dan orientasi kristal.

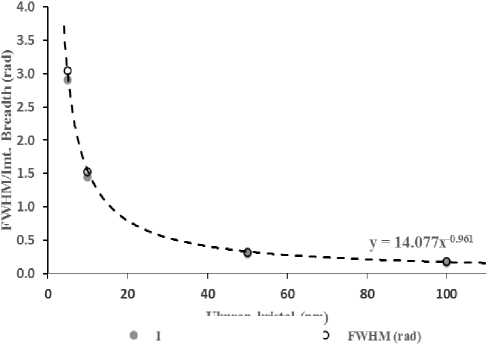
Luas puncak/kurva dari suatu difraksi sinar-X dipengaruhi oleh ukuran kristal sebagaimana diperlihatkan oleh formula Scherrer [3]. Hubungan ini ditunjukkan oleh nilai FWHM/Integral Breadth terhadap ukuran kristal terutama dalam ukuran orde nanometer, seperti diperlihatkan pada Gambar 1.

Gambar 1 memperlihatkan hubungan antara ukuran partikel terhadap FWHM dan Integral Breadth. Hal ini mengindikasikan bahwa profil kurva suatu puncak difraksi akan melebar terutama untuk ukuran kristal apabila ukuran partikel kurang dari 100 nm. Puncak-puncak difraksi pada spektra difraksi menunjukkan pelebaran (perluasan) karena ukuran dan regangan partikel [5]. Lebar puncak difraksi dapat digunakan untuk memperkirakan ukuran rata-rata partikel.

Ukuran kristal (nm)

Integral breadth (rad) C

Gambar 1. Hubungan antara FWHM (Full Width at Half Maximum)  terhadap ukuran kristal dan

Integral Breadth suatu puncak difraksi dalam skala nanometer [4].


Dalam artikel ini dideskripsikan metode menentukan ukuran kristal (crystallite size) dari data hasil karakterisasi XRD. Untuk tujuan tersebut digunakan formula Scherrer secara langsung dan “Scherrer Termodifikasi”, serta metode Williamson-Hull Plot. Sementara untuk menentukan ukuran partikel dari sampel yang sama digunakan metode karakterisasi SEM.

  • II.    LANDASAN TEORI

Secara gari besar yang berkontribusi terhadap pelebaran puncak (kurva) difraksi adalah faktor pelebaran instrument (Instrumental Breadth) dan pelebaran sampel (specimen broadening). Tanpa memperhatikan perluasan instrumentasinya, pelebaran suatu puncak difraksi dari pelebaran sampel dapat berasal dari akibat ukuran kristal dan microstrain (strain kisi akibat perpindahan unit sel di sekitar posisi normalnya [4, 5]. Dari data karakterisasi XRD, ukuran kristal dapat diperkirakan dengan menggunakan formula Scherrer [2, 5],

D =


Kλ β cos(θ)


(1)


dimana λ = panjang gelombang sinar-X yang digunakan, dan θ = sudut difraksi, K = adalah konstanta yang besarnya tergantung pada faktor bentuk kristal, bidang (hkl) difraksi, dan definisi besaran β yang digunakan, apakah sebagai Full Width at Half Maximum (FWHM) atau Integral Breadth dari puncak. Nilai K sebenarnya bervariasi dari 0,62 sampai 2,08. Nilai yang umumnya digunakan untuk K adalah: 0,94 jika β adalah FWHM dan 0,89 untuk Integral Breadth [2, 4]. Dari persamaan 1 dapat diamati bahwa lebar puncak bervariasi dengan sudut 2θ dalam bentuk cos(θ).

Lebar puncak difraksi juga dipengaruhi oleh mikrostrain (strain kisi), yaitu efek dari perpindahan suatu unit sel di sekitar posisi normalnya. Ini sering dihasilkan oleh beberapa faktor antara lain [4]: (1) Distorsi kisi yang tidak seragam, yang dapat diakibatkan oleh tegangan permukaan nanocrystal, morfologi bentuk kristal, dan pengotor interstisial. (2) Dislokasi, (3) Perbatasan domain antar fase, yang mana terbentuk pada saat penyusunan struktur material yang mengalami gangguan transformasi penyusunan. Kontribusi mikrostrain terhadap pelebaran FWHM dan Integral Breadth pada puncak difraksi diungkapkan dalam bentuk persamaan (2) [4-7].

βc (2θ)= Cε snθ (2) cos θ

Dimana ε=strain (perubahan ukuran yang terjadi dibagi ukuran semula) dan C = konstanta.

  • III.    METODA EKSPERIMEN

Untuk melakukan analisis ukuran kristal pada eksperimen ini digunakan data hasil karakterisasi XRD dari sampel campuran Gd0,95La0.05Ba2Cu3O7-δ. Sampel disintesis sebagaimana dilakukan pada penelitian sebelumnya [8]. Sampel berbentuk pelet dikarakterisasi dengan Difractometer XPERT-PRO dan SEM–AMETEX Hasil pengukuran XRD dianalisis dengan software Match-3.

  • 3.1    Menentukan Ukuran Kristal dengan Formula Scherer dan “Scherrer Termodifikasi”

Untuk menentukan ukuran kristal, dilakukan perhitungan dengan formula Scherrer persamaan 1, dengan mendefinisikan besaran β sebagai FWHM dan konstanta K dipilih 0,94. Dalam eksperimen ini dilakukan perhitungan pada setiap bidang hkl dari puncak-puncak difraksi yang sesuai dengan fase Gd0,95La0.05Ba2Cu3O7-δ. Dengan demikian diperoleh sejumlah N ukuran kristal sesuai dengan bidang hkl yang terukur.

Hasil perhitungan selanjutnya dibuat gambar distribusi ukuran kristal dalam bentuk diagram batang dengan software Origin-8. Diagram yang dihasilkan dianalisis dengan pendekatan Gaussian sehingga diperolen ukuran kristal rata-rata. Sebagai pembanding, dihitung juga ukuran kristal rata-rata =∑xi/N dari seluruh data ukuran kristal Xi hasil pehitungan.

Untuk metode Scherrer Termodifikasi, kedua suku (suku bagian kanan dan kirinya) dari formula Scherrer pada persamaan 1 diambil nilai logaritmanya sehingga diperoleh persamaan (3) [9].

ln(β ) = lnI — I + ln 1 (3) I D ) I. cos(θ))

Dari persamaan 3 dapat dibuat grafik antara ln(β)ln(1/cos(θ). Karena ln(β) terhadap ln(1/cos(θ) menunjukkan hubungan linier maka dapat dilakukan pendekatan Least Squares Fit to straight line dengan formula sebagaimana diberikan pada Apendik. Dengan demikian diperoleh persamaan garis lurus y = y0 + mx dengan standar error untuk y0 dan m masing-masing Δy0 dan Δm. Dari persamaan garis lurus tersebut diperoleh perpotongan pada y0 = ln(Kλ/D) atau

D= Kλ.exp(-y0) (4)

Jika nilai K dan λ diketahui maka ukuran kristal D dapat dihitung.

  • 3.2    Menentukan Ukuran Kristal dengan Metode Plot Williamson-Hull

Jika perluasan profil adalah murni karena ukuran kristal dan strain kisi (tidak ada Instrument Broadening), maka β 2= βc2 + βs2 atau β = βc + βs dimana βc adalah lebar kurva yang dihasilkan dari ukuran kristal, dan βs adalah kurva yang melebar karena strain kisi. Dengan demikian diperoleh persamaan (5) [5, 9].

βcos(θ) = Kλ +4εsin(θ)


(5)


Dengan memilih β adalah FWHM, maka persamaan (5) memperlihatkan hubungan linier antara FWHM.cos(θ) dan sin(θ). Oleh karena itu, grafik hubungan antara y = FWHM.cos(θ) terhadap x = sin(θ) dapat dilakukan pendekatan Least Squares Fit to straight line. Dengan demikian diperoleh persamaan garis lurus dengan gradien m = 4ε dan perpotongan pada sumbu y pada y0 = (Kλ)/D, atau

D=Kλ y0

(6)


Dengan demikian nilai ukuran kristal D dan strain ε dapat dihitung.

  • 3.3    Menentukan Ukuran Partikel dengan

SEM

Dari karakterisasi SEM diperoleh mikrograf, yang memperlihatkan morfologi permukaan sampel sehingga dapat teramati bentuk dan ukuran partikel (butiran). Dengan memperhatikan skala pada mikrograf dapat diketahui ukuran partikelnya. Ukuran partikel ditentukan dengan menggunakan software ImageJ sehingga diperoleh sejumlah N data ukuran partikel. Dengan software Origin-8 dibuat distribusi ukuran partikel dalam betuk diagram batang. Diagram dianalisis dengan pendekatan Gaussian sehingga diperoleh nilai ukuran partikel. Dalam menentukan ukuran partikel, juga dilakukan perhitungan rata-rata ukuran partikel dari seluruh titik xi data ukuran partikel secara langsung dengan persamaan ∑ xi/N.

  • 4.    HASIL

    • 4.1    Hasil XRD

Gambar 2 memperlihatkan pola spektrum difraksi sinar-X dari sampel fase Gd0,95La0,005Ba2Cu3O7-δ. Hasil Search-Match dengan software Match 3 dengan menggunakan referensi Ba2Cu3GdO7 dari COD (Crystallography Open Database) Entry 96153-9606, diperoleh fraksi volume sebesar 73,7%. Puncak-puncak difraksi yang sesuai (match) diperlihatkan pada Tabel 1.

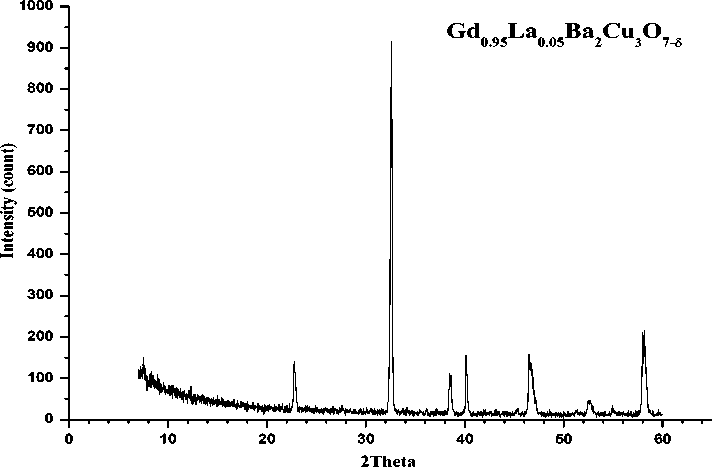
Gambar 2. Pola difraksi XRD dari sampel senyawa Gd0,95La0,005Ba2Cu3O7-δ.


Tabel 1. Puncak-Puncak Difraksi XRD dari sampel senyawa Gd0,95La0,005Ba2Cu3O7-δ.

No.

2theta (º)

d (Å)

I/I0

FWHM (º)

hkl

1

7,55

11,7051

26,50

0,1200

001

2

22,79

3,8996

121,76

0,1570

003

3

23,13

3,8429

6,25

0,1200

010

4

24,08

3,6923

19,53

0,1200

101

5

24,45

3,6379

14,83

0,1200

011

6

27,46

3,2450

19,93

0,1200

102

7

27,72

3,2156

18,32

0,1200

012

8

32,47

2,7552

537,96

0,1200

103

9

32,58

2,7461

10,0

0,1639

013

10

32,81

2,7273

51,12

0,1200

110

11

36,29

2,4732

0,08

0,1200

112

12

38,48

2,3374

107,90

0,1994

005

13

38,75

2,3218

21,57

0,0782

014

14

40,27

2,2378

52,89

0,1200

113

15

45,24

2,0026

11,84

0,2400

105

16

45,39

1,9967

15,07

0,2400

015

17

46,53

1,9502

194,95

0,1618

006

18

46,76

1,9410

124,60

0,1424

200

19

47,30

1,9201

11,57

0,1200

201

20

47,42

1,9156

16,52

0,1223

020

21

48,07

1,8912

11,72

0,1160

021

22

51,39

1,7766

12,20

0,2800

115

23

52,39

1,7450

24,94

0,1200

106

24

52,52

1,7411

42,59

0,3058

203

25

52.65

1,7370

30,25

0,1200

210

26

53,18

1,7211

6,70

0,1200

023

27

53,31

1,7171

6,42

0,1200

120

28

54,88

1,6716

23,12

0,2203

007

29

55,25

1,6613

12,59

0,2800

212

30

58,01

1,5885

249,57

0,1465

116

31

58,22

1,5834

166,71

0,1476

213

32

58,58

1,5745

13,83

0,1200

123

  • 4.2    Ukuran Kristal dengan Formula Scherer dan “Scherrer Termodifikasi”

Telah dihitung ukuran kristal dengan menggunakan persamaan 1 dengan FWHM dari puncak-puncak difraksi sinar-X pada Tabel 1. Hasil perhitungan untuk seluruh puncak difraksi diperoleh distribusi ukuran kristal seperti yang ditunjukkan oleh diagram batang pada Gambar 3. Dengan menganalisis diagram menggunakan pendekatan Gasuss, diperoleh kurva seperti tampak pada Gambar 3 dan data-data yang diperoleh diperlihatkan pada Tabel 2. Dari tabel tersebut

diperoleh nilai Xc (nilai pusat simetri dari kurva) yang merepresentasikan ukuran kristal, yaitu DSch = 63,1675±2,4316 nm. Sementara hasil peritungan secara langsung dari seluruh data diperoleh rata-rata ukuran kristal yaitu Dhkl ave = 64,0555±3,3254 nm.

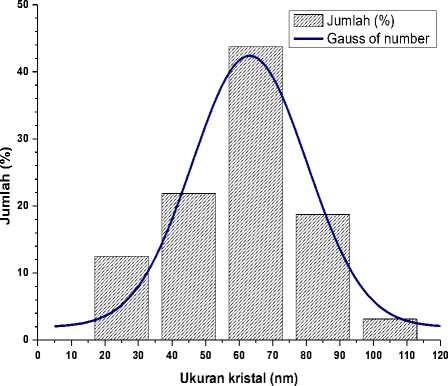
Gambar 3. Distribusi ukuran kristal. Kurva dibuat dengan pendekatan fungsi Gauss.

Tabel 2. Hasil analisis kurva Gauss pada Gambar 3.

y=y0 +

(A/(w.sqrt(π/2))).exp(-2.((x-xc)/w)2)

Parameter

Value

Standard Error

Y0

1,94907

3,1069

xc

63,16754

2,43162

w

34,07416

5,74262

A

1727,158

346,5778

sigma

17,03708

FWHM

40,11926

R-Square

40,44333

Sementara itu, dari data Tabel 1, dengan metode persamaan “Scherrer Termodifikasi” (persamaan (3)) diperoleh grafik seperti ditunjukkan pada Gambar 4. Garis lurus pada Gambar 4 diperoleh dengan melakukan Least Squares Fit to straight line dengan mendefinisisikan y=ln(β) dan x=ln(1/cos(θ). Diperoleh persamaan linier berikut.

y = 2,7846x-2,1309.

Dengan demikian diperoleh titik potong pada sumbu y, yaitu y0 = -2,1309. Dengan persamaan (4), yaitu D = Kλ.exp(-y0) maka ukuran kristal dapat dihitung, hasilnya adalah D = 67,0005±0,0215 nm.

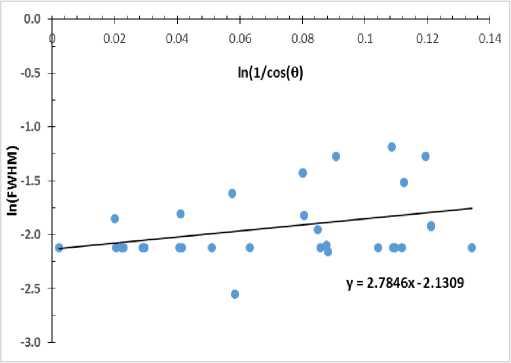
Gambar 4. Grafik ln(FWHN) terhadap ln(1/cos(θ)).

  • 4.3    Ukuran Kristal dengan Metoda Williamson-Hull Plot.

Dengan memperhatikan persamaan (5) dan dengan data XRD pada Tabel 1 dibuat grafik βcos(θ) terhadap sin(θ), hasinya seperti ditunjukkan pada Gambar 5. Dari defenisi y = βcos(θ) dan x = sin(θ), dengan melakukan Least Squares Fit to straight line diperoleh persamaan garis

y = 0,003376x + 0,001427

Dari titik potong garis pada sumbu y dan gradiennya, masing-masing dapat dihitung ukuran kristal dan faktor strain, hasilnya masing-masing adalah D = 97,3040± 0,1510 nm dan ε = 8,44%±3,96%.

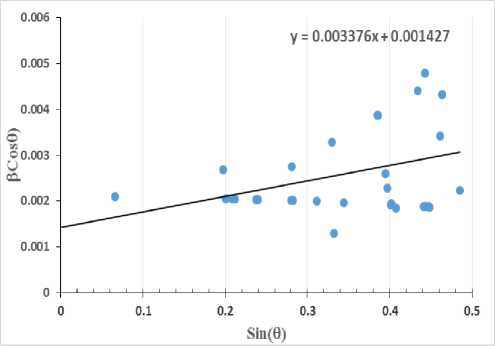
Gambar 5. Grafik hubungan antara βcos(θ) dan sin(θ).

  • 4.4    Ukuran Partikel dari Karakterisasi SEM

Gambar 6 memperlihatkan gambar morfologi sampel hasil sintesis fase Gd0,95La0.05Ba2Cu3O7-δ Tampak sampel terdiri atas butiran-butiran dengan ukuran kurang dari 10 µm. Butiran berbentuk memanjang posisi tidak teratur dan dengan ukuran

tidak sama. Dengan menggunakan software Image-J diperoleh distribusi ukuran partikel seperti tampak pada Gambar 7. Dengan menggunakan pendekatan kurva Gauss diperoleh data seperti ditunjukkan pada Tabel 3. Diperoleh bahwa nilai pusat simetri kurva sebagai representasi dari rata- rata ukuran butiran, yaitu D = 94,1097 ± 2,4687 nm. Hasil perhitungan rata-rata secara langsung dari seluruh titik data diperoleh, D = 98,7297 ± 2,2735 nm.

Gambar 6. Hasil karakterisai SEM dari sampel senyawa Gd0,95La0.05Ba2Cu3O7-δ.

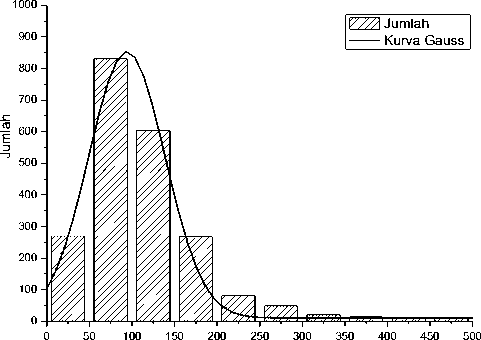
Ukuran Butir (nm)

Gambar 7. Distribusi ukuran butiran dari gambar SEM Gambar 6. Kurva pada gambar diperoleh dengan pendekatan Gauss

Tabel 3. Data hasil analisis Gauss pada Gambar 7.

Parameter

Nilai

Std error

Y0

10,36874

10,39016

Xc

94,10966

2,4687

w

89,70143

5,03693

A

94707,45

5110,884

sigma

44,85071

FWHM

105,6154

Heigh

842,4126

  • 5.    PEMBAHASAN

Dari data karakterisasi XRD, dengan melakukan perhitungan menggunakan persamaan Scherrer diperoleh ukuran kristal rata-rata, DSch= 63,1675±2,4316 nm. Hasil ini mendekati hasil perhitungan rata-rata langsung dari seluruh titik data, yaitu Dhkl ave = 64,0555 ±3,3254 nm. Sedangkan dengan metode grafis, dengan persamaan Scherrer Termodifikasi diperoleh ukuran kristal rata-rata D=67,0005± 0,0215 nm. Dari hasil tersebut tampak terdapat perbedaan sekitar ~6%, meskipun keduanya menggunakan rumus dasar yang sama. Perbedaan tersebut terjadi karena penggunaan pendekatan distribusi Gauss pada Gambar 3 yang pada dasarnya adalah memberikan probabilitas tertinggi (yang paling mungkin) dari ukuran kristal. Sedangkan Least Squares Fit to straight line pada Gambar 4 adalah memberikan nilai rata-rata dari keseluruhan data ukuran kristal. Dengan demikian penggunaan Scherrer Termodifikasi memberikan ukuran kristal yang lebih akurat.

Dalam perhitungan ukuran kristal dengan melibatkan faktor strain dalam Metode Plot Williamson-Hull memberikan ukuran kristal D=97,3040±0,1510 nm. Nilai tersebut lebih besar dari pada yang diberikan oleh persamaan Scherrer maupun persamaan Scherrer Termodifikasi. Hal ini mengindikasikan adanya faktor lain yang berpengaruh terhadap puncak/kurva pada spekra difraksi.

Semakin kuatnya strain mengakibatkan bertambah lebarnya puncak-puncak difraksi sehingga bertambahnya mikrostrain kisi dan mengakibatkan berkurangnya ukuran kristal [7]. Oleh karena itu, faktor strain ε=8,44%±3,96% seharusnya memberikan efek pelebaran terhadap kurva difraksi dan mengakibatkan semakin kecilnya ukuran kristal yang terukur. Dengan pemperhatikan hasil search-match yang meghasilkan fraksi volume dari fase Gd0,95La0.05Ba2Cu3O7-δ adalah 73,7%, hal ini menunjukan adanya fase lain, sampel bersifat polikristal. Besarnya ukuran kristal yang diperoleh mengindikasikan bahwa fase lain yang terbentuk adalah kristal dengan ukuran kristal yang lebih besar dari ukuran kristal fase Gd0,95La0.05Ba2Cu3O7-δ yang terbentuk.

Hal tersebut konsisten dengan hasil pengukuran SEM pada Gambar 7 yang memberikan ukuran partikel sebesar D=94,10966±2,4687 nm, dan dari perhitungan secara langsung dari seluruh data yaitu ukuran butiran rata-rata yaitu D=98,7297±2,2751 nm. Nilai ini hampir sama dengan nilai hasil pengukuran dengan metode grafis Plot Williamson-Hull pada Gambar 5, yang melibatkan faktor strain.

Ini menunjukkan bahwa kecilnya efek dari strain terhadap pelebaran kurva puncak difraksi.

Perlu dipahami bahwa dalam skala bulk, ukuran partikel tidak identik dengan ukuran kristal. Kristal adalah bagian dari grain, sedangkan grain adalah bagian dari pada partikel, sehingga ukuran kristal < butiran (grain) < partikel. Dalam skala nanometer (kurang dari 100 nm), pada material kristal berdomain tunggal, ukuran kristal (crystallite size) adalah sama dengan ukuran grain dan hampir sama dengan ukuran partikel (particle size) [10].

  • 6.    KESIMPULAN

Sampel yang diperoleh adalah bersifat polikristal, terdapat 26,3% fase lain yaitu selain fase Gd0,95La0.05Ba2Cu3O7-δ. Hasil pengukuran ukuran kristal dengan menggunakan keempat metode memberikan hasil yang berbeda. Pengukuran dengan persamaan Scherrer dan Scherrer Termodifikasi memberikan hasil yang lebih kecil dari pada menggunakan metode grafis Williamson-Hull Plot dan SEM. Hasil pengukuran dengan metode Williamson-Hull Plot dan SEM lebih merepresentasikan ukuran kristal/butiran secara keseluruhan di dalam sampel. Sedangkan hasil pengukuran dengan persamaan Scherrer dan Scherrer Termodifikasi lebih merepresentasikan ukuran kristal dari fase tertentu saja (fase tunggal), dalam hal ini fase Gd0,95La0.05Ba2Cu3O7-δ.

APENDIKS

Dalam eksperimen, sering diperlukan untuk menentukan fungsi y=ƒ(x), yang menggambarkan relasi/hubungan antara kedua variabel yang diukur dari suatu gambar grafik. Bagaimana harus membuat garis (kurva) yang sesuai dengan titik-titik data dalam gambar tersebut? Untuk data dengan kecendrungan membentuk garis lurus y = y0 + mx dapat dilakukan dengan meteode Least Squares Fit to straight line.

Jika N adalah jumlah pengukuran, xi adalah variabel bebas ke-i, dan yi adalah variabel terikat dari variabel bebas xi, maka untuk menentukan titik potong y0 dan gradient m dilakukan langkah-langkah perhitungan sebagai berikut. Pertama dihitung [11],

Sxx=∑xi2-(∑xi)(A1)

Syy =∑yi2-(∑yi)2

S = xy -∑xi∑yi(A3)

xyi i

Dari persamaan A1 dan A3 dapat dihitung gradien m:

Sxy

m =

Sxx

dan titik potong y0:

∑ y. y o = N

—


∑ xt

m

N


(A4)


(A5)


Selanjutnya, diperoleh,


dengan persamaan A1, A2 dan A4

S


Standar error persamaan:


Δ m =


Sv - m2 Sxx yy         xx

N—2

(A6)


untuk gradien m dihitung dengan

Sy2

Sxx


(A7)


Sedangkan standar error untuk y0 dihitung dengan persamaan:

δy o =


Koefisien persamaan


Sy2

V N — (∑ χl)2/∑ x

determinasinya dihitung

(A8)


dengan


(N ∑ xy — ∑ χ∑ y. )2


R2


4 (N ∑ x; — (∑ x, )■)( N ∑ y; — (∑ y. )2

PUSTAKA

  • [1]    Rao CNR, Kulkarni GU, Thomas PJ, et al. Size-Dependent Chemistry:  Properties of

Nanocrystals. Chem A Eur J, vol. 8, 2002, pp. 28.

  • [2]    Satoshi Horikoshi and Nick Serpone, Microwaves in Nanoparticle Synthesis, First Edition. Edited by Satoshi Horikoshi and Nick Serpone, Wiley-VCH Verlag GmbH & Co. KGaA, 2013, Chap. 1.

  • [3]    Harold P. Klug, Leroy E. Alexander, X-Ray Difraction Properties, New York, John Wiley & Son Inc., 1962, Chap. 9.

  • [4]    Scott A Speakman, Estimating Crystallite Size Using XRD, MIT Center for Materials Science and Engineering.

http://prism.mit.edu/XRAY/oldsite/CrystalSize Analysis.pdf

  • [5]    V. S. Vinila, Reenu Jacob, Anusha Mony, Harikrishnan G. Nair, Sheelakumari Issac, Sam

Rajan, Anitha S. Nair, D. J. Satheesh1, Jayakumari Isac, Ceramic Nanocrystalline Superconductor Gadolinium Barium Copper Oxide (GdBaCuO) at Different Treating Temperatures, Journal of Crystallization Process and Technology, vol. 4, 2014, pp. 168176. http://dx.doi.org/10.4236/jcpt.2014.43021

  • [6]    S. Dinilchenko, O. Kukharenko, C. Moseke, I. Protsenko, L. Sukhodub and B. Sulkio-Cleff, “Determine Bone Mineral Crystallite Size and Lattice Strain from Diffraction Line Broadening,” Research and Technology Crystal, vol. 37, no. 11, 2002, pp. 1234-1240.

  • [7]    S. Gencalp  Irizalp, N. Saklakoglu, Laser

Peening of Metallic Materials, Reference Module in Materials Science and Materials Engineering    Comprehensive    Materials

Finishing, vol. 1, 2017, pp. 408–440.

https://doi.org/10.1016/B978-0-12-803581-8.09160-8.

  • [8]    Made Sumadiyasa, I. Gusti Agung Putra Adnyana, Nyoman Wendri, Putu Suardana, Synthesis and Characterization of GLBCO-123 Phase: Gd1-xLxBa2Cu3O7-δ (x = 0.0 - 0.5), Journal of Materials Science and Chemical Engineering, 2017, vol. 5, pp. 49 - 57.

http://www.scirp.org/journal/msce

  • [9]    Ahmad Monshi, Mohammad Reza Foroughi, Mohammad Reza Monshi, Modified Scherrer Equation to Estimate More Accurately NanoCrystallite Size Using XRD, World Journal of Nano Science and Engineering, vol. 2, 2012, pp. 154 - 160.

http://dx.doi.org/10.4236/wjnse.2012.23020.

  • [10]    Qing Li, Christina W. Kartikowati, Shinji Horie, Takashi Ogi, Toru Iwaki & Kikuo Okuyama, Correlation between particle size/domain structure and magnetic properties of highly crystalline  Fe3O4  nanoparticles,

Scientific Reports, vol. 7: 9894, 2017, pp.– 7.

http://dx.doi.org/10.1038/s41598-017-09897-5.

  • [11]    Douglas A. Skoog, James J. Leary, Principles of Instrumentatl Analysis, 4th     edition,

Sounders College Publisher, New York, 1992, pp. 985.

34