PENENTUAN PRODUK RADAR CUACA PALING TEPAT UNTUK MEMBUAT PERINGATAN DINI CUACA EKSTRIM DENGAN MENGGUNAKAN METODE ANALYTICAL HIERARCY PROCESS (AHP)
on
Buletin Fisika Vol. 16 No. 1 Pebruari 2015 : 25-38
PENENTUAN PRODUK RADAR CUACA PALING TEPAT Untukmembuat peringatan dini Cuacaekstrim DENGAN MENGGUNAKAN METODE ANALYTICAL HIERARCYPROCESS (AHP)
Kadek Sumajas, Komang Ngurah Suarbawa 1, Decky Irmawan2
Terjadinya fenomena cuaca yang bersifat tidak normal atau berbeda dari keadaan biasanya cenderung berpotensi menyebabkan bencana dan atau menimbulkan korban jiwa. Salah satu fasilitas yang ditemukan untuk bisa melakukan prakiraan cuaca jangka pendek dalam waktu singkat adalah RADAR Cuaca. RADAR Cuaca menghasilkan berbagai macam produk yang memiliki keunggulan masing-masing untuk digunakan baik dalam analisa kejadian cuaca, prediksi hujan, badai, pergerakan angin, mengetahui intensitas hujan, dan berbagai macam kegunaan lainnya berdasarkan berbagai kriteria yang ditentukan . Dari sekian banyak produk yang dihasilkan, terdapat empat produk RADAR Cuaca yang sering digunakan untuk untuk membuat peringatan dini cuaca ekstrim yaitu produk PPI, CMAX, UWT, dan TRACK. Masalah muncul pada pemilihan beberapa pilihan produk RADAR Cuaca dalam waktu yang relatif singkat yang mungkin saja antara produk satu dan lainnya mempunyai kelebihan dan kekurangan masing-masing.
Dalam penelitian ini, penulis bermaksud menerapkan metode Analytical Hierarchy Process (AHP) untuk menentukan produk RADAR Cuaca paling tepat untuk membuat peringatan dini cuaca ekstrim. Pembahasan difokuskan pada produk RADAR cuaca yang di gunakan, yaitu PPI, CMAX, UWT, dan TRACK dengan responden merupakan prakirawan di wilayah kerjanya yang dilengkapi fasilitas RADAR cuaca dan ahli dalam menggunakan RADAR cuaca untuk melakukan peringatan dini cuaca ekstrim dan pengolahannya menggunakan metode Analytic Hierarchy Process (AHP).
-
II. TINJAUAN PUSTAKA
Cuaca ekstrim didefinisikan sebagai kejadian cuaca yang tidak normal, tidak lazim yang dapat mengakibatkan kerugian terutama keselamatan jiwa dan harta (Peraturan Kepala BMKG Kep.009 Tahun 2010). Beberapa unsur yang menyebabkan terjadinya cuaca ekstrem tersebut (Pasal 1) dan dapat dideteksi oleh RADAR CUACA cuaca antara lain.
-
1. Angin kencang adalah angin dengan kecepatan e” 25 knots (45 km/jam).
-
2. Angin puting beliung adalah angin kencang yang berputar yang keluar dari awan Cumulonimbus (awan hitam yang bergumpal seperti bunga kol) dengan kecepatan e” 34.8 knots (64.4 km/jam).
-
3. Waterspout adalah angin puting beliung yang terjadi di lautan atau wilayah perairan luas lainnya dengan kecepatan e” 34.8 knots (64.4 km/jam).
-
4. Hujan lebat adalah hujan dengan intensitas minimal 50 mm dalam 24 jam atau 20 mm/ jam.
-
5. Hujan es adalah hujan yang bebrbentuk butiran es yang mempunyai garis tengah paling rendah 5 mm dan berasal dari awan Cumulonimbus.
-
6. Badai tropis kecepatan adalah sistem tekanan rendah dengan angin berputar siklonik yang terbentuk di lautan wilayah tropis dengan kecepatan angin e” 34,8 knots atau 64,4 km/jam disekitar pusat putaran.
Prediksi cuaca ekstrim dilakukan dengan mempertimbangkan gejala fisis atau dinamis
atmosfer yang cenderung akan memburuk atau menjadi ektrim sesuai dengan skala meteorologi (pasal 4). Skala meteorologi yang mampu diamati RADAR Cuaca meliputi skala lokal dan skala regional, yang dikarenakan luas wilayah cakupan RADAR Cuaca secara umum hanya mencapai skala ratusan kilometer.
RADAR Cuaca adalah alat bantu untuk mengamati cuaca secara khusus berupa hujan, awan, arah, dan kecepatan angin dalam radius yang cukup luas hingga ratusan kilometer (tergantung panjang gelombang yang digunakan) dengan resolusi ± 300m. Output berupa image dapat diinterpretasikan atau dianalisa hingga menghasilkan suatu informasi yang berguna untuk pelayanan jasa meteorologi. (Zakir A. dkk, 2010).
Untuk membantu prakirawan dalam melakukan analisa, prediksi cuaca serta untuk mampu menghasilkan peringatan dini cuaca ekstrim yang cepat, tepat, akurat, dan mudah dipahami, Badan Meteorologi Klimatologi dan Geofisika membangun suatu sistem jaringan RADAR Cuaca yang saling terintegrasi dengan menggunakan beberapa merk yaitu RADAR Cuaca EEC dari Amerika Serikat, RADAR Cuaca Gematronic dari Jerman, dan RADAR Cuaca Baron Amerika Serikat.
Setiap RADAR Cuaca dengan nama produksinya masing-masing memiliki beberapa produk yang hampir sama yang bisa digunakan untuk melakukan analisa cuaca, pengamatan cuaca, prediksi, peringatan dini cuaca ekstrim dan lain sebagainya, beberapa produk yang dihasilkan RADAR Cuaca tersebut antara lain PPI (Plan Position Indicator), MAX atau CMAX (Maksimum Produk), SRV atau TRACK - Storm
Tracking, UWT (Uniform Wind Technique), CAPPI (Constant Altitude Plan Position Indicator), ETOP (Echo Top ∕ Height Product), EBASE (Echo Base ∕ Height Product), VIL (Vertically Integrated Liquid), ACM (Accumulated Precipitation), HMAX (Height of the Maximum ), dll.
Dari sekian banyak produk yang dihasilkan dengan berbagai kegunaan masing-masing dalam berbagai kegiatan analisa dan prakiraan cuaca, adapun Produk RADAR Cuaca yang sering digunakan untuk membuat peringatan dini cuaca ekstrim yang akan digunakan untuk pengolahan lebih lanjut pada penelitian ini adalah produk PPI, CMAX, UWT, dan TRACK.
-
2.3 Metode AHP (Analytical Hierarcy
Process)
Metode AHP merupakan sebuah hierarki fungsional dengan input utama yang berupa persepsi manusia yang memecahkan suatu masalah yang kompleks dan tidak terstruktur ke dalam kelompok-kelompok yang kemudian diatur menjadi suatu bentuk hierarki sehingga permasalahan akan tampak lebih terstruktur dan sistematis. Menurut Saaty (1994), hierarki didefinisikan sebagai suatu representasi dari sebuah permasalahan yang kompleks dalam suatu struktur multi level dimana level pertama adalah tujuan, yang diikuti level faktor, kriteria, sub kriteria, dan seterusnya ke bawah hingga level terakhir dari alternatif.
AHP digunakan untuk menentukan prioritas dari beberapa kriteria dengan melakukan analisa perbandingan berpasangan (Pairwise Comparison) dari masing-masing kriteria, dimana untuk melakukan proses komputasi AHP perlu untuk memahami lebih dahulu prinsip kerja AHP, sebagai berikut.
-
1. Penentuan Komponen Keputusan
-
a) Tujuan/Sasaran yang ingin dicapai
-
b) Kriteria (komponen-komponen yang ingin diperbandingkan antara 1 dan lainnya)
-
c) Alternatif (komponen yang disediakan dan merupakan pilihan yang akan diperbandingkan satu dengan lainnya berdasarkan kriteria yang ada)
-
2. P enyusunan hirarki dari komponen keputusan
-
3. Penilaian Alternatif dan Kriteria
-
4. Pemeriksaan Konsistensi Penilaian
-
5. Penentuan Prioritas Kriteria dan Alternatif
Kriteria dapat dinilai dengan cara memberi nilai 1-9, seperti tabel 2.1.
Tabel 2.1 Bobot Nilai Kriteria
Nilai Keterangan
-
1 Sama Penting (Equal)
-
2 Antara Equal dan Moderate
-
3 Cukup lebih penting (Moderate)
-
4 Antara Moderate dan Strong
-
5 Lebih penting (Strong)
-
6 Antara Strong dan Very Strong
-
7 Sangat lebih penting (Very Strong)
-
8 Antara Very Strong dan Extreme
-
9 Mutlak lebih penting sekali (Extreme)
Dengan struktur hierarki pemilihan produk RADAR Cuaca seperti gambar 2.2.
Penelitian dilakukan dengan melibatkan responden yang dalam penelitian ini adalah para prakirawan memiliki kapasitas dalam menginformasikan secara dini cuaca ekstrim di beberapa Unit Pelaksana Teknis (UPT) BMKG di Indonesia yang memiliki fasilitas RADAR cuaca.
Dengan tujuan memilih produk radar yang paling tepat untuk membuat peringatan dini cuaca ekstrim, ditentukanlah enam kriteria yaitu Realtime (kesesuaian produk diakses dengan waktu pengamatannya), Running (kecepatan produk tersebut bisa dihasilkan), Identifikasi (kemudahan produk tersebut digunakan ), Fenomena (jumlah fenomena cuca yang dapat diidentifikasi), Luasan (luas wilayah fenomena cuaca yang mampu dicakup), dan Verifikasi (kesesuaian hasil prakiraan). Dengan alternatif pilihan dari setiap kriteria tersebut adalah PPI, CMAX, UWT, dan TRACK.
Dalam menggunakan AHP sebagai sistem pendukung keputusan, Saaty (1994) menyusun tahapan-tahapan analisis yang disajikan dalam diagram alir pada gambar 3.2. Sistem ini dimulai
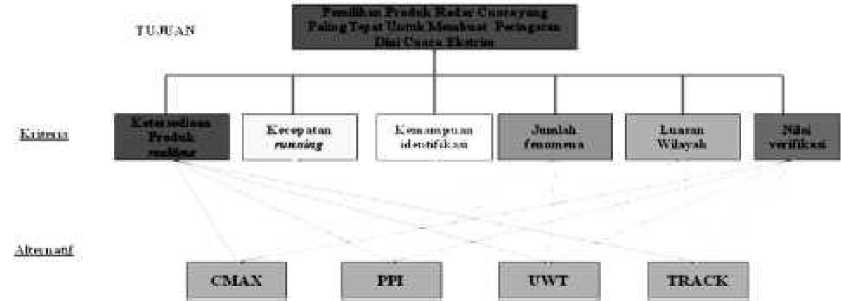
Gambar 2.2 Hierarki pemilihan produk RADAR Cuaca
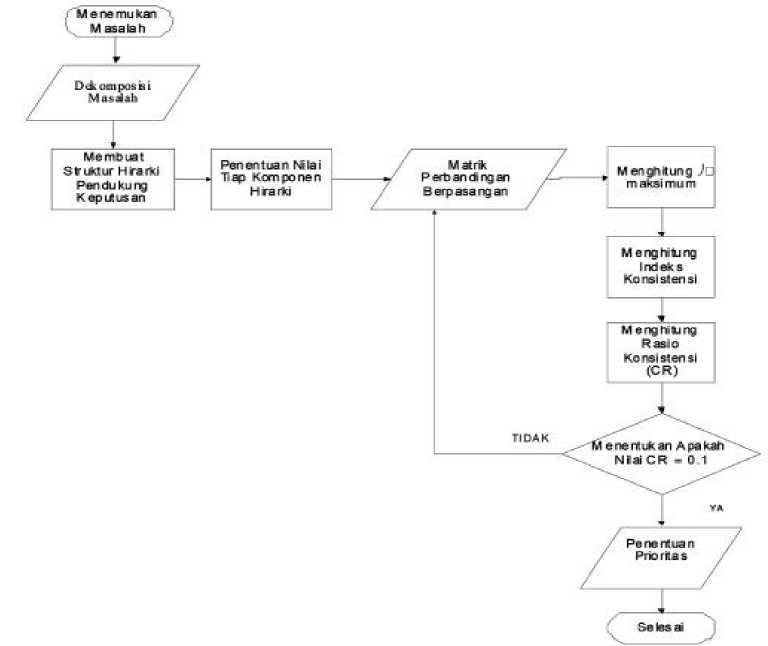
Gambar 3.2 Diagram alir pemilihan produk RADAR Cuaca
dengan menemukan masalah, dekomposisi masalah, membuat struktur hierarki pendukung keputusan, penentuan nilai tipa komponen hierarki, matrik perbandingan berpasangan, menghitung vektor eigen maksimum, menghitung indeks konsistensi, menghitung rasio konsistensi, dan penentuan prioritas.
Nilai uji konsistensi diperlukan untuk menghitung konsistensi jawaban responden dengan tahapan sebagai berikut.
-
a) Menentukan vektor eigen dengan cara mengubah matriks ke bentuk desimal kemudian hitung setiap baris matriks hasil perkalian tersebut dan jumlahkan selanjutnya normalisasi matrik tersebut (membagi jumlah
tiap baris matriks hasil perkalian dengan jumlah totalnya).
-
b) Mencari nilai vektor eigen maksimum (■ ..-' yaitu dengan mengalikan total matriks sebelum dinormalisasi dengan eigen vektor.
-
c) Menentukan Consistency Index (CI) dengan menggunakan persamaan
CI = (emaχ-n)∕(n-l), dengan n menyatakan kuantitas variabel
-
d) Menghitung Consistency Ratio (CR) dengan rumus CR = CI∕RI. Hasil penghitungan akan dianggap konsisten apabila nilai
-
konsistensinya d” 0.1. Random Indexs (RI) diperoleh dari tabel 3.1.
Tabel 3.1 Random Index (RI)
|
RC |
0 |
0 |
0,58 |
0,90 |
1,12 |
1,24 |
1,32 |
1,41 |
1,45 |
1,49 |
Data yang diperoleh dari hasil pendapat Responden akan diolah menjadi hasil perbandingan kriteria, perbandingan alternatif kriteria realtime, perbandingan alternatif kriteria kecepatan running, perbandingan alternatif kriteria kemampuan identifikasi, perbandingan alternatif kriteria fenomena, perbandingan alternatif kriteria luasan, dan perbandingan alternatif kriteria verifikasi. Dimana sebagai langkah awal untuk
menentukan data yang layak dipakai maka perlu dilakuakan uji konsistensi terhadap semua data yang diperoleh.
Dari data hasil perbandingan kriteria kita akan menyusun matriks kriteria kedalam bentuk matriks reciprocal nya masing-masing, sebagai berikut.
|
— Realtime Running Identifikasi Fenomena Luasan Verifikasi — | |
|
Realtime Running Identifikasi Fenomena Luasan |
1 2 263/495 1 49/90 2 541/790 2 376/609 2 261/533 32/81 1 1 388/405 2 41/579 2 69/91 2 76/229 90/139 405/793 1 2 187/743 2 635/686 2 125/402 349/937 466/965 298/671 1 2 336/799 2 47/260 115/301 91/251 269/787 302/731 1 2 274/931 |
|
Verifikasi |
194/483 229/534 402/929 260/567 316/725 1 |
Dari matriks diatas dapat dilihat nilai perbandingan antar kriteria berdasarkan tingkat kepentingannya. Nilai matriks resiprocal menunjukkan nilai kebalikan tingkat kepentingan kriteria kedua terhadap kriteria pertama dari
tingkat kepentingan kriteria pertama terhadap kriteria kedua. Kemudian nilai pecahan dalam matriks akan diubah kedalam bentuk desimal untuk mempermudah perhitungan, Hasilnya dapat ditunjukkan pada matriks berikut.
|
— Realtime |
Running |
Identifikasi |
Fenomena |
Luasan |
Verifikasi | |
|
Realtime |
1.000000 |
2.531314 |
1.544444 |
2.684811 |
2.617406 |
2.489683 |
|
Running |
0.395052 |
1.000000 |
1.958025 |
2.070813 |
2.758251 |
2.331876 |
|
Identifikasi |
0.647482 |
0.510719 |
1.000000 |
2.251683 |
2.925657 |
2.310944 |
|
Fenomena |
0.372466 |
0.482902 |
0.444112 |
1.000000 |
2.420525 |
2.180768 |
|
Luasan |
0.382058 |
0.362549 |
0.341804 |
0.413133 |
1.000000 |
2.294308 |
|
Verifikasi |
0.401658 |
0.428839 |
0.432724 |
0.458554 |
0.435861 |
1.000000 |
Pada matriks desimal diatas jumlah tiap baris dibagi dengan total jumlah ke enam baris, akan diperoleh bobot relatif yang dinormalkan atau ternormalisasi yang disebut sebagai vektor eigen. Hasilnya dapat ditunjukkan pada matriks berikut.
Dengan menggunakan cara yang sama dengan uji konsistensi hasil perbandingan kriteria diperoleh nilai eigen maksimum ( , nilai
Vektor
|
1.000000 2.531314 1.544444 2.684811 2.617406 2.489683 0.395052 1.000000 1.958025 2.070813 2.758251 2.331876 0.647482 0.510719 1.000000 2.251683 2.925657 2.310944 0.372466 0.482902 0.444112 1.000000 2.420525 2.180768 0.382058 0.362549 0.341804 0.413133 1.000000 2.294308 0.401658 0.428839 0.432724 0.458554 0.435861 1.000000 |
Eigen 12.867658 0.268745 10.514017 0.219589 9.646485 0.201470 6.900773 0.144125 4.793851 0.100121 3.157636 + 0.065948 + |
|
3.198715 5.316323 5.721109 8.878995 12.157700 12.607578 |
47.880420 1.000000 |
Selanjutnya nilai eigen maksimun diperoleh kolom dengan vektor eigen. Nilai eigen maksimum
dengan menjumlahkan hasil perkalian jumlah ( ■ :..;.. ..■ yang diperoleh adalah
= (3.198715 «0.268746) +(5.316323* 0.219589)+ (5.721109 * 0.201470)
+ (S.878995» 0.144125)+ (12.157700* 0.100121)+ (12.607578* 0.065948)
- 6.508Q62
Karena matriks yang terbentuk adalah matriks berorde enam yang terdiri dari enam kriteria maka nilai indeks konsistensi (CI) yang diperoleh adalah
⅛∣gimiB n
n - 1
6.508062- 6
CI =-------------- 0.101612
6—1
indeks konsistensi (CI), dan nilai rasio konsistensi (CR) untuk perbandingan alternatif pada semua kriteria. Nilai tersebut dapat dilihat pada tabel 4.1.
Tabel 4.1 Nilai _,,_._, CI, dan CR untuk
perbandingan alternatif pada semua kriteria
Untuk n„6, indeks konsistensi acak (RI) „ 1.24 (tabel Saaty), maka nilai rasio konsistensi (CR) adalah
CR =
0.101612
1.24
0.08194J
Karena CR < 0,1 berarti data dari responden tersebut konsisten dan bisa dilanjutkan dengan pengolahan data berikutnya untuk mendapatkan nilai bobot kepentingan perbandingan kriteria.
|
Kriteria e . . maksimum |
CI |
CR |
|
Kriteria 6.508062 |
0.101612 |
0.081945 |
|
Realtime 4.216956 |
0.072319 |
0.080354 |
|
Running 4.263287 |
0.087762 |
0.097517 |
|
Identifikasi 4.260440 |
0.086813 |
0.096459 |
|
Fenomena 4.248446 |
0.082815 |
0.092017 |
|
Luasan 4.262885 |
0.082815 |
0.097365 |
|
Verifikasi 4.263878 |
0.087959 |
0.097732 |
Karena untuk semua kriteria nilai CR < 0,1 berarti data dari responden tersebut konsisten dan bisa dilanjutkan dengan pengolahan data berikutnya untuk mendapatkan nilai bobot kepentingan tiap kriteria.
Dengan menggunakan matriks yang telah dikonversi kedalam bentuk desimal, selanjutnya
Iterasi I
akan dilakukan penentuan prioritas. Pembobotan pada tiap tingkatan hierarki dilakukan melalui jalan iterasi atau perkalian matriks (baris kalikan dengan kolom). Proses iterasi minimal sebanyak tiga kali karena akan dicari selisih nilai vektor eigen dengan nilai vector eigen dua iterasi berikutnya, dengan banyak maksimum yang relatif hingga diperoleh nilai vektor eigen yang stabil atau selisihnya nol.
|
1.000000 |
2.531314 |
1.544444 |
2.684811 |
2.617406 |
2.489683 |
|
0.395052 |
1.000000 |
1.958025 |
2.070813 |
2.758251 |
2.331876 |
|
0.647482 |
0.510719 |
1.000000 |
2.251683 |
2.925657 |
2.310944 |
|
0.372466 |
0.482902 |
0.444112 |
1.000000 |
2.420525 |
2.180768 |
|
0.382058 |
0.362549 |
0.341804 |
0.413133 |
1.000000 |
2.294308 |
|
0.401658 |
0.428839 |
0.432724 |
0.458554 |
0.435861 |
1.000000 |
|
X | |||||
|
1.000000 |
2.531314 |
1.544444 |
2.684811 |
2.617406 |
2.489683 |
|
0.395052 |
1.000000 |
1.958025 |
2.070813 |
2.758251 |
2.331876 |
|
0.647482 |
0.510719 |
1.000000 |
2.251683 |
2.925657 |
2.310944 |
|
0.372466 |
0.482902 |
0.444112 |
1.000000 |
2.420525 |
2.180768 |
|
0.382058 |
0.362549 |
0.341804 |
0.413133 |
1.000000 |
2.294308 |
|
0.401658 |
0.428839 |
0.432724 |
0.458554 |
0.435861 |
1.000000 |
Vektor
|
— |
Eigen | |
|
6.000000 9.164517 11.209607 16.312092 24.319137 |
26.311284 |
0.299467 |
|
4.819623 6.000000 7.397698 11.819935 18.307853 |
21.016431 |
0.222592 |
|
4.381377 5.799477 6.000000 9.567715 15.412234 |
19.047599 |
0.193218 |
|
3.023960 3.948205 4.180026 6.000000 9.397742 |
12.994673 |
0.126905 |
|
2.204057 3.050163 3.159832 4.424487 6.000000 |
8.076073 |
0.086373 |
|
1.590230 2.474858 2.678092 4.037954 5.481813 |
6.000000 |
0.071445 + 1.000000 |
Selanjutnya kita masuk pada iterasi II, langkah-langkah yang dilakukan dalam proses iterasi pada prinsipnya sama dengan iterasi yang
telah dilakukan pada tahap pertama. Matriks yang akan dikalikan adalah matriks yang dihasilkan pada iterasi I.
Hasil iterasi II
Vektor
Eigen
|
274.051881 |
378.681563 |
417.804994 |
625.162902 |
929.907732 |
1130.230375 |
0.300039 |
|
199.763084 |
277.594437 |
306.339756 |
457.102673 |
677.207203 |
821.367772 |
0.218837 |
|
173.719696 |
241.672154 |
267.720875 |
399.936016 |
592.004380 |
714.534806 |
0.190894 |
|
115.008317 |
160.158169 |
177.761552 |
266.040022 |
394.254060 |
473.993830 |
0.126796 |
|
81.216014 |
112.582360 |
125.311713 |
187.942539 |
279.994477 |
336.689960 |
0.089771 |
|
67.037204 |
92.466605 |
102.471560 |
153.525512 |
228.987130 |
277.608296 |
0.073663 |
1.000000
Kemudian dilanjutkan pada iterasi III dengan melakukan proses iterasi yang pada prinsipnya sama dengan iterasi yang telah dilakukan pada
tahap sebelumnya dengan matriks yang akan dikalikan adalah matriks yang dihasilkan pada iterasi II.
Hasil iterasi III
|
Vektor Eigen | ||||||
|
446521.804 |
619194.8416 |
685835.3091 |
1026125.459 |
1524281.482 |
1842490.087 |
0.299944 |
|
845 |
95 |
80 |
400 |
837 |
049 | |
|
326048.697 |
452138.4588 |
500797.8859 |
749274.4848 |
1113016.175 |
1345367.068 |
0.219018 |
|
458 |
60 |
45 |
59 |
694 |
287 | |
|
284370.393 |
394344.8502 |
436787.0383 |
653504.4324 |
970750.9717 |
1173390.804 |
0.191022 |
|
629 |
68 |
64 |
87 |
72 |
656 | |
|
188784.398 |
261793.6990 |
289971.5681 |
433845.4558 |
644457.8114 |
778978.8006 |
0.126815 |
|
228 |
68 |
06 |
25 |
69 |
15 | |
|
133442.057 |
185047.1453 |
204966.1610 |
306665.2132 |
455541.7517 |
550626.7686 |
0.089639 |
|
989 |
55 |
53 |
47 |
21 |
83 | |
|
109508.631 |
151856.2644 |
168201.1099 |
251658.2825 |
373832.9934 |
451870.2500 |
0.073561 |
|
465 |
61 |
01 |
83 |
66 |
13 |
1.000000 |
Pada hasil iterasi III selanjutnya dilakukan perhitungan selisih antara hasil iterasi I dan iterasi III untuk melihat konsistensi nilai-nilai vektor eigen hasil normalisasi .
Tabel 4.2 Selisih nilai vektor eigen iterasi I dengan III untuk perbandingan kriteria
|
Vektor Eigen I |
Vektor Eigen III |
Selisih |
|
0.299467 |
0.299944 |
0.000477 |
|
0.222592 |
0.219018 |
0.003574 |
|
0.193218 |
0.191022 |
0.002196 |
|
0.126905 |
0.126815 |
0.000090 |
|
0.086373 |
0.089639 |
0.003266 |
|
0.071445 |
0.073561 |
0.002116 |
Hasil pada tabel 4.2 menunjukkan bahwa demikian, maka proses iterasi diteruskan ke iterasi masih terdapat selisih hingga desimal ke 6 pada IV.
semua elemen penyusun matriks, dengan
Hasil iterasi IV
|
Vektor Eigen | ||||||
|
11951889539 |
16573922007 |
18357780713 |
27466325673 |
40800260957 |
49317158166 |
0.299944 |
|
50.910000 |
95.000000 |
52.230000 |
04.440000 |
20.300000 |
29.13 0000 | |
|
87272290865 |
12102221473 |
13404789031 |
20055817576 |
29792211763 |
36011221135 |
0.219018 |
|
1.662000 |
08.400000 |
49.550000 |
95.520000 |
65.120000 |
43.640000 | |
|
76116937790 |
10555286562 |
11691356818 |
17492234978 |
25984099958 |
31408180668 |
0.191023 |
|
5.515000 |
31.030000 |
32.440000 |
30.420000 |
97.350000 |
80.970000 | |
|
50531910611 |
70073601559 |
77615654918 |
11612606602 |
17250118759 |
20851014558 |
0.126815 |
|
8.099000 |
1.444000 |
7.899000 |
74.010000 |
53.550000 |
63.040000 | |
|
35718589766 |
49531676068 |
54862792719 |
82083959693 |
12193283570 |
14738584515 |
0.089639 |
|
2.988000 |
1.560000 |
5.899000 |
8.345000 |
56.720000 |
11.350000 | |
|
29311983893 |
40647508777 |
45022418492 |
67361105801 |
10006255397 |
12095022641 |
0 073561 |
|
5.547000 |
1.640000 |
8.146000 |
4.740000 |
15.130000 |
27.930000 |
1.000000 |
Pada hasil iterasi IV selanjutnya dilakukan perhitungan selisih antara hasil iterasi II dan iterasi IV untuk melihat konsistensi nilai-nilai vektor eigen hasil normalisasi.
Hasil pada tabel 4.3 menunjukkan bahwa masih terdapat selisih hingga desimal ke 6 pada semua elemen penyusun matriks, dengan demikian, maka proses iterasi diteruskan ke iterasi V.
Hasil iterasi V
Tabel 4.3 Selisih nilai vektor eigen iterasi II dengan IV untuk perbandingan kriteria
|
Vektor Eigen II |
Vektor Eigen IV |
Selisih |
|
0.300039 |
0.299944 |
0.000095 |
|
0.218837 |
0.219018 |
0.000181 |
|
0.190894 |
0.191023 |
0.000128 |
|
0.126796 |
0.126815 |
0.000018 |
|
0.089771 |
0.089639 |
0.000132 |
|
0.073663 |
0.073561 |
0.000101 |
|
Vektor | ||||||
|
19678628241 |
292319102686 |
3533395886 |
Eigen 0.299944 | |||
|
85630962735 |
11874615249 |
131526854483 |
1064700000 | |||
|
24050000000 |
88980000000 |
046000000000 |
09110000000 |
983000000000 |
OOOOOO OOO | |
|
000.000000 |
0000.000000 |
00.000000 |
0000.000000 |
00.000000 |
000 2580073656 |
0.219018 |
|
62527437707 |
86708036628 |
960404617428 |
14369267402 |
213450414431 |
R667700000 | |
|
71000000000 |
78190000000 |
785000000000 |
98840000000 |
834000000000 |
OOOOOO OOO | |
|
000.000000 54535030983 |
000.000000 75624807882 |
0.000000 837643400848 |
0000.000000 12532553255 |
00.000000 186166671642 |
000 2250282467 5724800000 OOOOOO 000 |
0.191023 |
|
12540000000 |
59660000000 |
285000000000 |
89910000000 |
866000000000 | ||
|
000.000000 |
000.000000 |
0.000000 |
0000.000000 |
00.000000 |
000 1493899725 |
0.126815 |
|
36204285023 |
50205199302 |
556088075610 |
83200123292 |
123590857484 |
9615800000 | |
|
97690000000 |
30190000000 |
490000000000 |
33600000000 |
045000000000 |
OOOOOO 000 | |
|
000.000000 |
000.000000 |
0.000000 |
000.000000 |
00.000000 |
000 1055966236 |
0.089639 |
|
25591076785 |
35487653175 |
393072053026 |
58810186207 |
873604635977 |
374I600000 | |
|
98330000000 |
58190000000 |
129000000000 |
72000000000 |
506000000000 |
OOOOOO 000 | |
|
000.000000 |
000.000000 |
0.000000 |
000.000000 |
0.000000 |
000 8665645960 |
0.073561 |
|
21000975555 |
29122468862 |
322569333290 |
48261794268 |
716911982974 |
3841400000 | |
|
222I0000000 |
30260000000 |
580000000000 |
18240000000 |
510000000000 |
00000 0000 | |
|
000.000000 |
000.000000 |
0.000000 |
000.000000 |
0.000000 |
00 |
1.000000 |
Pada hasil iterasi IV selanjutnya dilakukan perhitungan selisih antara hasil iterasi II dan iterasi IV untuk melihat konsistensi nilai-nilai vektor eigen hasil normalisasi .
Tabel 4.4 Selisih nilai vektor eigen iterasi III denganV untuk perbandingan kriteria
|
Vektor Eigen III |
Vektor Eigen V |
Selisih |
|
0.299944 |
0.299944 |
0.000000 |
|
0.219018 |
0.219018 |
0.000000 |
|
0.191022 |
0.191022 |
0.000000 |
|
0.126815 |
0.126815 |
0.000000 |
|
0.089639 |
0.089639 |
0.000000 |
|
0.073561 |
0.073561 |
0.000000 |
Hasil pada tabel 4.4 menunjukkan bahwa tidak terdapat selisih hingga desimal ke 6 pada semua elemen penyusun matriks, dengan demikian maka proses iterasi dihentikan pada iterasi V. Nilai pembobotan yang digunakan adalah nilai eigen hasil normalisasi iterasi V, sehingga tiap-tiap elemen penyusun kriteria dapat di susun seperti pada tabel 4.5.
Pada perhitungan perbandingan kriteria setelah iterasi ke-5 seperti pada tabel 4.5 diperoleh nilai kriteria realtime yang paling penting dengan bobot kepentingan 29.99%, kemudian kriteria
Tabel 4.5 Nilai bobot tiap-tiap elemen penyusun kriteria
|
Kriteria |
Bobot |
|
Realtime |
0.299944 |
|
running |
0.219018 |
|
Identifikasi |
0.191022 |
|
Fenomena |
0.126815 |
|
Luasan |
0.089639 |
|
Verifikasi |
0.073561 |
running dengan bobot kepentingan 21.90%, diikuti oleh kriteria identifikasi dengan bobot kepentingan 19.10%, kriteria fenomena dengan bobot kepentingan 12.68% , luasan dengan bobot kepentingan 8.96% dan kriteria verifikasi dengan bobot 7.36%. Nilai bobot perbandingan kriteria jika ditampilkan dalam struktur hierarki dapat dilihat pada gambar 4.1.
Dari struktur hierarki diatas dapat dilihat nilai bobot untuk setiap kriteria dengan nilai bobot tertinggi adalah kriteria Realtime. Langkah selanjutnya yaitu melakukan sintesis atau penentuan prioritas untuk menentukan bobot dari setiap alternatif PPI, CMAX, UWT dan TRACK sebagai penyusun kriteria realtime, running, identifikasi, fenomena, luasan, dan verifikasi.
Peinililiaii Produk Radar Cuaca yang Paling Tepat IiiitiikMeinbiiat Peringatan Dini Cuaca Ekstrim
|
ReitZtitiie |
Running |
Identiflkasi |
Fenomena |
Luasan |
Verifikasi |
|
(0.299944) |
(02190181 |
(0.191022) |
(0.126815) |
(0.089639) |
(0.0'3561) |
Gambar 4.1 Nilai bobot perbandingan kriteria dalam struktur hierarki
Setelah melakukan penetapan prioritas pada perbandingan kriteria, selanjutnya penetapan prioritas atau pilihan dilakukan pada alternatif. Dengan melakukan prosedur dan jumlah iterasi yang sama seperti proses sistesis atau penentuan prioritas matriks perbandingan kriteria , maka nilai bobot tiap-tiap alternatif penyusun semua kriteria untuk tiap-tiap elemen alternatif penyusun kriteria realtime, running, identifikasi, fenomena, luasan, dan verifikasi dapat disusun seperti tabel 4.6.
Dari tabel 4.6 dapat dilihat bobot setiap alternatif untuk setiap kriteria, dimana nilai bobot
PPI dan CMAX dominan memiliki nilai tertinggi, diikuti oleh UWT dan TRACK. Setelah didapatkan nilai bobot perbandingan kriteria dan bobot dari setiap alternatif PPI, CMAX, UWT dan TRACK sebagai penyusun kriteria realtime, running, identifikasi, fenomena, luasan, dan verifikasi, akan dilanjutkan perhitungan matrik gabungan untuk menentukan alternatif terbaik.
Setelah matriks individu tersusun untuk masing-masing kriteria dan alternatif, maka akan terbentuk profil hierarki beserta pembobotannya seperti gambar 4.3.
Tabel 4.6 Nilai bobot tiap-tiap alternatif penyusun semua kriteria
|
AlternatifZKriteria |
Realtime Running Identifikasi Fenomena Luasan Verifikasi |
|
PPI |
0.502322 0.429882 0.474861 0.392853 0.444380 0.395799 |
|
CMAX |
0.279508 0.309711 0.282572 0.370737 0.336548 0.355616 |
|
UWT |
0.105493 0.140844 0.128509 0.137017 0.124478 0.145322 |
|
TRACK |
0.112678 0.119563 0.114057 0.099394 0.094594 0.103263 |
Peinililiim ProihikRiidtu' Cii⅛h « yangPaliiig Tepnt UiitukItIeLnbiim PeiTJigiitnik Dini Cuncii KktfiTin
|
Prwhk Γι,ιιltιιm' (0.299944) |
Kecepaton /Hitiliftg (0.219018) |
KeinatnpDOii identifikasi (0.191025) |
Jumlah fenmυeιuι (0.126815) |
Luasan ∖vilay ah (0.0896 59) |
Nilai ⅞erifikasi (0.0"3561) | |||||||||||
|
PFl 0.502322 CMAN 0.279508 VWT 0.105-193 TRACK 0.112678 |
PPI 0.429882 CMAN 0.309711 VWT 0.140844 TRWK 0.119563 |
I1Pl 0.474861 CMAN 0.2 82 572 IJWT 0.128509 TRACK 0.114057 |
PPI 0.392853 CMAX 0.3 70 73 7 UWT 0.137017 TRACK 0.099394 |
PPI 0.444380 CMAN 0.336548 UWT 0.124478 TRACK 0.094594 |
PPI 0.395799 CMAX 0.355616 UWT 0.145322 TRACK 0.103263 | |||||||||||
Gambar 4.3 Nilai bobot perbandingan kriteria dan alternatif dalam struktur hierark
Langkah selanjutnya yaitu menetukan alternatif terbaik dengan menggabungkan antara hasil pembobotan pada kriteria dan pembobotan alternatif berdasarkan kriteria. Untuk itu akan dibuat matriks gabungan dengan menyusun
matriks hasil pembobotan alternatif berdasarkan kriteria yang telah dilakukan sebelumnya, kemudian lakukan perkalian silang dengan masing-masing bobot kriteria yang diperoleh pada analisis perbandingan kriteria, sebagai berikut.
|
— | ||||
|
PPI |
0.502322 |
0.429882 |
0.474861 |
0.392853 |
|
CMAX |
0.279508 |
0.309711 |
0.2 825 72 |
0.370737 |
|
UWT |
0.105492 |
0.140844 |
0.128509 |
0.137017 |
|
TRACK |
0.112678 |
0.1 19563 |
0.114057 |
0.099394 |
|
0.299944 | |||
|
0.444380 |
0.395799 |
0.219018 | |
|
0.336548 |
0.355616 |
0.191023 | |
|
0.124478 |
0.145322 |
X |
0.126815 |
|
0 094594 |
0.103263 |
0.089639 | |
|
0.073561 |
|
- - | |
|
PPI |
0.454299 |
|
CMAX |
0.308989 |
|
UWT |
0.12626! |
|
TRACK |
0.110451 |
Dari hasil diatas diperoleh PPI memiliki tingkat kepentingan paling tinggi dengan bobot 45.43%, diikuti produk CMAX dengan bobot kepentingan 30.9%, kemudian produk UWT dengan bobot kepentingan 11.05% dan yang terakhir produk TRACK dengan bobot kepentingan 11.01%.
-
V. KESIMPULAN DAN SARAN
Berdasarkan pengolahan data dan pembahasan yang telah dilakukan, didapatkan beberapa kesimpulan sebagai berikut:
-
1. Metode Analytical Hierarchy Process (AHP) dapat membantu pengambilan keputusan dalam penentuan produk RADAR Cuaca paling tepat untuk membuat peringatan dini cuaca ekstrim secara obyektif, meskipun berasal dari pendapat yang berbeda-beda.
-
2. Sesuai hasil penentuan prioritas pemilihan alternatif produk dalam penentuan produk RADAR Cuaca paling tepat untuk membuat peringatan dini cuaca ekstrim, diperoleh produk PPI memiliki tingkat kepentingan paling tinggi, diikuti produk CMAX, kemudian produk UWT dan yang terakhir produk TRACK.
Kepada pembaca jika ingin melakukan penelitian lebih lanjut tentang AHP disarankan menggunakan menggunakan kriteria dan alternatif lebih banyak untuk memperoleh hasil yang lebih baik dan menggunakan program aplikasi tambahan seperti Expert Choice, Super Decisions dan lain sebagainya agar lebih mudah dalam melakukan perhitungan dan mengurangi kesalahan dalam penggunaan angka yang banyak. Disarankan untuk melakukan penelitian yang sama tetapi dengan menggunakan metode dari sistem
pendukung keputusan yang lain supaya bisa dibandingkan hasilnya dengan penelitian ini.
DAFTAR PUSTAKA
Peraturan Kepala BMKG No: KEP.009 Tahun 2010 tentang Prosedur Standar
Operasional Pelaksanaan Peringatan Dini, pelaporan dan Diseminasi Informasi Cuaca Ekstrim. Oktober 2010.
Saaty, Thomas L. 1994. Fundamentals of decision making and priority theory with analytic hierarchy process. RWS Publications. Pittsburgh PA 15260, USA.
Sinaga, Johannes. 2009. Penerapan Analytical Hierarchy Process (AHP) dalam Pemilihan Perusahaan Badan Usaha Milik Negara (BUMN) sebagai Tempat Kerja
Mahasiswa Universitas Sumatera Utara (USL). Skripsi.
Utari, Lis. 2011. Rancang Bangun database Nilai Siswa tingkat Sekolah Menengah
Memilih Kendaraan dengan Metode Analytic Hierarchy Process dan Super Decision. Jurnal Ilmiah Teknologi dan Informasi Volume 2 - Mei 2011.
Herujono, 2000. Modul Pendahuluan Radar Cuaca. Badan Pendidikan dan Latihan Perhubungan Akademi Meteorologi dan Geofidika (AMG). Jakarta
Zakir, A., Sulistya, W., dan Khotimah M. K., 2010. Prespektif Operasional Cuaca Tropis. Badan Meteorologi Klimatologi dan Geofisika. Jakarta
Rinehart, R. E., 1997. RADAR for Meteorologists. Rinehart Publishing. Collumbia Enterprise Electronics
Corporation. (2007). EDGE 5 Manual. Enterprise Electronics Corporation. Alabama, USA
BMKG [Badan Meteorologi Klimatologi dan Geofisika]. 2013. Modul Diklat Teknis Analisa Cuaca. Jakarta : BMKG Pusat.
38
Discussion and feedback