Analysis of Semester 4 Student Procedural Error Knowledge In Determining Minimum Path Using Dijkstra Algorithm
on
Udayana Journal of Social Sciences and Humanities, p-ISSN: 2549-6956, e-ISSN: 2621-9107
DOI: https://doi.org/10.24843/UJoSSH.2019.v03.i02.p06
| 91
Analysis of Semester 4 Student Procedural Error Knowledge In Determining Minimum Path Using Dijkstra Algorithm
Zaini
Lecturer Department Eletrical Engineering Sekolah Tinggi Teknologi Bontang zaini.math@gmail.com
Abstract The focus of this research is the determination of the shortest route by students by applying the Dijkstra algorithm which has many benefits in the informatics area. The sample of this research were 4 students who had heterogeneous abilities. The results showed that 75% of the failed samples due to calculation errors. Students with high abilities are easier to understand and skilled at using procedural knowledge compared to students with medium and low abilities.
Keywords: Procedural knowledge, minimum path, algorithm Dijkstra.
-
I. INTRODUCTION1
Mathematics learning in schools continues to be oriented to place students in various roles through discussion, investigation, discovery, project completion, problem-solving, and so on. The purpose is for students are able and able to construct their knowledge. This realization is a form of learning meaning reform as in the 4 pillars are learning to know, learning to do, learning to be, and learning to live together (Maclean, 2005). By its role, students can build relationships to collaborate ideas, grow critical and creative nature, a satisfaction of thought, and self-pride which in turn can be an ability to investigate, solve problems, develop ideas (Sedaghat et al., 2018). But in practice, not a few of them have failed. For example in problem solving, it is known that students of basic education for all levels of age and ability fell difficulties (Babakhani, 2011). Difficulties are also faced by students in high education in proving Euclid's Geometry theorem (Zaini, 2014) and statistics calculations (Putro and Darminto, 2015). These failures occur due to errors that include concept errors, procedural errors (Kastolan, 1992), miscalculations and concluding (Putro and Darminto, 2015), low ability to analyze information, to the ability of prerequisites those are not mastered.
Other causes are views of students at the basic education and medium education and university students at the higher education level declaring
mathematics as a difficult lesson. This assumption makes students are afraid to learn mathematics so students become passive in learning (Trianto, 2007). From the difficulties they experienced, the acquisition of answers to the questions given in the conditions of guessing and careless answered without thinking first, so that cause mistakes. Mistakes that are often experienced and made by students and students are mistakes in completing mathematical tasks. Related to mathematical tasks, Polya gives four principals in solving them, namely (1) understand the problem, (2) devise a plan, (3) carry out the plan, and (4) review / extend (Polya, 2019).
Quite a lot of mistakes occur besides routine math tasks, namely mathematics problems in the form of daily life implementation and high-level thinking problems (HOTS) (Abdullah et al., 2017) and set story problems (Natsir, Tandiayuk, B. and Karniman, S., 2016). Related to implementation problems, mathematical material is very identical to daily life that students should be familiar with. Mathematical material that is pretty much applied in real life is a graph. More than that, the graph is also used for information technology, including determining the shortest route.
The methods for determining the shortest route are quite diverse including Genetic Algorithm (Philip, Taofiki, Adio and Kehinde, 2011), Ant Colony Optimization (Zaidi and Gupta, 2018), Algorithm of Branch and Bound (Tunon and Lopez, 2005), Floyd-Warshall (Zaidi and Gupta, 2018) Generous, 2019). From the available methods, Dijkstra's algorithm is practically used in routing and other network-related protocols (Miglani, Khera and
Aggarawal, 2016), efficient (Yao et al., 2016), and faster convergence time (Attamimi, 2017). Some problems that can be solved by Dijkstra's algorithm include finding the shortest path between two particular nodes (a pair of shortest paths), finding the shortest path between every pair of vertices (all pairs of shortest paths), finding the shortest paths from the specific node to all other nodes (single-source shortest path), and finding the shortest path between two vertices through several specific nodes (intermediate shortest path) (Novandi, 2007). It is further stated that Dijkstra's algorithm has 100% accuracy in determining the shortest route (Sahputra et al., 2016).
Dijkstra's algorithm is a material in a weighted graph that is contained in discrete mathematics courses and is given to level 4 students. The objectives to be achieved in this material are capable and apply the Dijkstra algorithm to solve the shortest route problems by well and fluently. Dijkstra's algorithm cannot be separated from conceptual knowledge because it has a procedure. Ramlah, et all (2013) told that procedural Knowledge is the knowledge of algorithms or task completion
procedures that can be given through demonstrations exemplified by the teacher (Purnomo et al., 2018). By mastering procedural knowledge, students have the potential to apply it well in the area of information technology. Therefore, this studying is intended to provide a procedural error experienced by students in determining the minimum route using the Dijkstra algorithm. By knowing the forms of procedural errors, lecturers can choose the right strategy in giving the right level of scaffolding to students for the next academic year.
This studying involved 4 levels, 4 students who have different abilities, namely 1 student has a high ability, 2 students have a medium ability, and 1 student has a low ability. Each student is given a problem that involves their NIM digit as a form of weighting. With this involvement, each student gets a question that has a different weighting and a different answer. The form of the questions given is a daily problem related to the minimum route. The minimum route search only focuses on the Dijkstra algorithm.
Picture 1. The test question
Terdapat tujuh tempat yang dapat diakses sebagaimana data berikut
|
Tempat |
Jarak yang dimiliki |
|
Rumah Eko |
5 km ke Mall 8 km ke Kampus X 4 km ke Lapangan Futsal |
|
Mall |
12 km ke Masjid |
|
Lapangan Futsal |
5 km ke Masjid 4 km ke Gedung Bioskop |
|
Kampus X |
10 km ke Masjid |
|
Option 1 : Rumah Ani |
(p + 1) km ke Masjid (q + 3) km ke Gedung Bioskop |
|
Option 2 : Rumah Ani |
(p + 2) km ke Masjid (q + 4) km ke Gedung Bioskop |
Saat ini, Eko berada di rumahnya. Eko mengagendakan akan bertemu dengan Ani di rumahnya untuk mengerjakan soal Matematika. Rancanglah rute terpendek atas perjalanan Eko ke Rumah Ani!
Keterangan:
-
- option 1: digunakan jika NIM genap
-
- option 2: digunakan jika NIM Genap
-
- nilai p dan q merupakan digit akhir pada NIM anda (NIM: 20170 0 0 Opq)
Triangulation of this research data includes solving questions by students and unstructured interview data regarding the steps to solve them. The review of conceptual knowledge errors in this studying combines 3 theories, namely problem-solving steps
referring to Polya (known, data collection, review), Putro and Darminto (aspects: calculation results and conclusion), and Kastolan (incompatible calculations and stages according to the algorithm). The problemsolving code developed can be observed in Picture 2.
Picture 2. Question thinking code
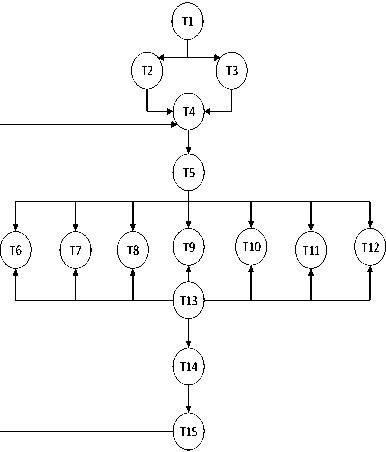
T5 Table of studying
T6 Determination of key 1 and calculation of minimum weight.
T7 Determination of key 2 and calculation of minimum weight.
T8 Determination of key 3 and calculation of minimum weight.
T9 Determination of key 4 and calculation of minimum weight
T10 Determination of key 5 and calculation of minimum weight
T11 Determination of key 6 and calculation of minimum weight
T12 Determination of key 7 and calculation of minimum weight
T13 Recheck the moving of key in every point
T14 Arranging conclusion
T15 Review again to T4.
All of the data and then analyzed through data reduction step, data studying and arranging conclusion.
Explanation :
T1 Digging information is known in question
T2 Review weight graph
T3 Understand step of Dijkstra’s .algorithm.
T4 Illustration of the graph.
-
III. FINDINGS AND DISCUSSION
Students in the fourth level who take discrete mathematics courses do not yet have a comprehensive picture related to graphs. They only know the shape of the image without knowing if it is a graph. The picture presented is a case of the Konigsberg bridge.
Picture 3 Map Konigsberg bridge (Shields, 2012) and studying in graph form.
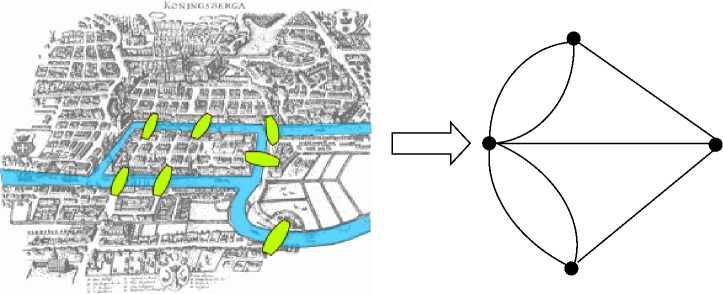
The first step to introduce a graph is to provide an example and not an example and the procedure for presenting it as a graph. Then involve students in arranging a formal definition. This activity is also applied to the introduction of the shortest route through examples arranged in the problems of daily
life. Giving example aims so that students can internalize it as a tool to solve problems (Irawan, 2015).
Visualization of questions in the form of graphs and their weighting were displayed well by four students. This indicates that the concept of graph for
all students with different abilities can master well. From this achievement, it can be said that the thinking is by the thought code that has been
compiled, namely T1, T2, T3, and T4. Visualization of the questions following the graph (consisting of points and lines) is shown as Picture 4.
Picture 4 graph studying following the concept

The graph presentation they have completed then becomes the material to investigate the shortest route according to the stages in the Dijkstra algorithm. They began their investigation by compiling a table containing the input of each point. The starting point is the point that originates from Eko's house and the endpoint of the route is at Ani's house. All students can go through this stage (Code thinking T5 is reached). SF investigation in finding the shortest route is following the code of thinking questions, namely A - D - F - G which weighs 12. The minimum weighting that has become a key has been
successfully added to another weighting by SF which then makes a comparison with the weighting operation of the previous weighting. SF managed to do it until the end of the shortest route discovery process without any calculation error
AF, KA, and DM have failed in determining the shortest route, especially in the calculation. Each of the three students, namely AF, KA, and DM, learned that the discrepancy of thinking with the code of thinking about the problem occurred in T7. The location of their error is shown in Picture 5
Picture 5 the mistakes of three students.
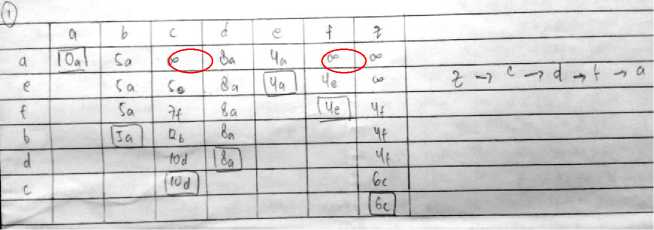
Failure with code thinking T7 cause not achieving the desired shortest route. In the Dijkstra method, if there is an error in the initial procedure then it results in an error for the next step. The error he experienced was due to a miscalculation in the thinking code T7, namely the minimum key weights (A to E with a weighting of 4) were not added with weights E to C or weights E to F. When they set point E as a key (starting from the thinking code T6) then weighting point E to C becomes 9E and weighting point E to F becomes 8E. In the code of thinking, T7 should be the key point C, but the three students chose point F as the key. Selection of keys at point F which causes the initial error.
The results of interviews conducted on the three students to review again the results obtained through the visualization of graph images, then they simultaneously said that there was another route that had the shortest route. They then realized that there
was a miscalculation in the process. They are allowed to do a repeat of their calculations carefully. The three students then said that their thinking errors occurred in the thinking code T7 to T15
Visualization in the form of graphs shown by students can be a good measure of the level of understanding of their concepts. While the procedure on Dijkstra's algorithm was not well mastered by the three students. This indicates the procedural knowledge possessed by students only reached 25% were in the T7 thinking code they had experienced calculation errors. The results of the study note that the students' logical and creative competencies were noted to be rather low for university-level mathematical studies. Almost 50% of students lacked competence in procedural work, while around 54% lacked conceptual competency. (Tularam and Hulsman, 2013). This finding can be a study of mathematics lecturers to strengthen students
'procedural knowledge in the following years and still pay attention to students' conceptual knowledge
Analysis of the results of the study found that 75% of the samples used failed in applying their procedural knowledge and they were compared to their conceptual knowledge. The failure was caused by a miscalculation that resulted in the determination of the weighting key is not right. Students who have high ability are easier to achieve conceptual and procedural understanding to be skilled in applying both than those who have the medium and low ability. Accuracy and carefulness in solving problems are the most important things in applying their procedural knowledge.
Acknowledgment
Thank you and give the highest appreciation to (1) Chair-person of the Institute for Research and Community Service at Sekolah Tinggi Teknologi Bontang which provides financial support so that research can be done correctly, (2) students involved in research activities, and (3) the entire academic community who participated in the success of this research was completed.
References
Abdullah, A. H. et al. (2017) ‘Analysis of Students ’ Errors in Solving Higher Order Thinking Skills ( HOTS ) Problems for the Topic of Fraction’, Asian Social Science, 11(21), pp. 133–142. DOI: 10.5539/ass.v11n21p133.
Attamimi, I. (2017) ‘Analisis Perbandingan Algoritma Floyd-Warshall dan Dijkstra untuk Menentukan Jalur Terpendek Pada Jaringan Openflow’, Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer (J-PTIIK) Universitas Brawijaya, 1(12), pp. 1842–1849.
Babakhani, N. (2011) 'The Effect of Teaching The Cognitive and Meta-Cognitive Strategies (SelfInstruction Procedure) On Verbal Math ProblemSolving Performance of Primary School Students With Verbal Problem - Solving Difficulties', Procedia - Social and Behavioral Sciences. Elsevier B.V., 15, pp. 563–570. DOI:
10.1016/j.sbspro.2011.03.142.
Dermawan, T. S. (2019) ‘Comparison of Dijkstra dan Floyd-Warshall Algorithm to Determine the Best Route of Train’, IJID (International Journal on Informatics for Development), 7(2), p. 8. DOI: 10.14421/ijid.2018.07202.
Irawan, E. B. (2015) ‘Pembuatan Contoh Pivotal-Bridging Dalam Interaksi Pembelajaran
Matematika’, in Seminar Nasional Matematika dan Pendidikan Matematika. UNY, pp. 1131– 1136.
Kastolan, D. (1992) Identifikasi Jenis-Jenis
Kesalahan Menyelesaikan Soal-Soal Matematika yang Dilakukan Peserta Didik Kelas II Program A1 SMA Negeri Se-Kotamadya Malang. Malang: IKIP Malang.
Maclean, R. (2005) Learning To Do Values for Learning and Working Together in a Globalized World. Edited by L. R. Leo, Joy de; Quisumbing. Germany: Unesco-Unevoc.
Miglani, V., Khera, S. and Aggarawal, A. (2016) ‘Intrusion Protection System in Dijkstra ’ s Algorithm’, International Journal of Engineering Science and Computing, 6(5), pp. 5303–5306. DOI: 10.4010/2016.1299.
Natsir, N., Tandiayuk, B., M. and Karniman, S., T. (2016) ‘Profile Kesalahan Konseptual dan
Prosedural Siswa Dalam Menyelesaikan Soal Cerita Himpunan Di Kelas VII SMPN 1 SINIU’, Jurnal Elektronik Pendidikan Tadulako, 3(4).
Novandi, R. A. D. (2007) ‘Perbandingan Algoritma Dijkstra dan Algoritma Floyd-Warshall dalam Penentuan Lintasan Terpendek ( Single Pair Shortest Path )’, Strategi Algoritmik. Available at: http://informatika.stei.itb.ac.id/~rinaldi.munir/St mik/2006-
2007/Makalah_2007/MakalahSTMIK2007-021.pdf.
Philip, A., Taofiki, Adio, A. and Kehinde, O. (2011) ‘A Genetic Algorithm for Solving Travelling Salesman Problem’, International Journal of Advanced Computer Science and Applications, 2(1), pp. 26–29.
Polya, G. (2019) ‘How to Solve It’, Wikipedia. Available at:
https://en.wikipedia.org/wiki/How_to_Solve_It.
Purnomo, E. A. et al. (2018) ‘Analyzing Student’s Errors in Resolving Questions of Statistics Education in Pokjar Boja, 2018.1’, in International Seminar on Education and Development of Asia. Semarang: Universitas
Muhammadiyah Semarang, pp. 332–336.
Putro, E. P. and Darminto, B. P. (2015) ‘Analisis Kesalahan Dalam Menyelesaikan Soal Ujian Akhir Semester Statistika Dasar Pada Mahasiswa Program Studi Pendidikan Matematika’, Ekuivalen, 18(1), pp. 63–68.
Sahputra, M. F. A. et al. (2016) ‘Implementation of
Traveling Salesman Problem ( TSP ) based on Dijkstra ’ s Algorithm in Logistics System’, 14(1), pp. 39–44.
Sedaghat, A. et al. (2018) ‘Laptop Riser, a Useful PBL Project for Diploma Students in Engineering Design’, Journal of Problem Based Learning in Higher Education, 6(1).
Shields, R. (2012) ‘Cultural Topology: The Seven Bridges of Königsburg 1736’, Theory Culture and Society, pp. 43–57. Available at: https://id.wikipedia.org/wiki/Tujuh_Jembatan_Kö nigsberg.
Trianto (2007) Model Pembelajaran Inovatif. Jakarta: Bumi Aksara.
Tularam, G. A. and Hulsman, K. (2013) 'A study of first-year tertiary students' mathematical knowledge conceptual and procedural knowledge, logical thinking and creativity', Journal of Mathematics and Statistics, 9(3), pp. 219–237. DOI: 10.3844/jmssp.2013.219.237.
Tunon, M. I. . and Lopez, M. . (2005) ‘Design and use of the CPAN Branch & Bound for the solution of the Traveling Salesman Problem (TSP)’, in International Conferences on Electronics, Communication, and Computers. Conielecomp. Available at:
https://www.researchgate.net/publication/221632 543_Design_and_Use_of_the_CPAN_Branch_Bo und_for_the_Solution_of_the_Travelling_Salesm an_Problem_TSP.
Yao, B. et al. (2016) ‘Path Optimization Algorithms Based on Graph Theory’, International Journal of Grid and Distributed Computing, 9(6), pp. 137– 148.
Zaidi, T. and Gupta, P. (2018) ‘Traveling salesman problem with ant colony optimization algorithm for cloud computing environment’, International Journal of Grid and Distributed Computing, 11(8), pp. 13–22. DOI:
10.14257/ijgdc.2018.11.8.02.
Zaini (2014) ‘Konstruksi Melalui Aktivitas Think Pair Share Pada Pembelajaran Matematika’, in Prosiding Seminar Nasional Matematika. Universitas Jember, pp. 233–243. Available at: http://id.portalgaruda.org/index.php?page=3&ipp =10&ref=browse&mod=viewjournal&journal=77 16.
Discussion and feedback