Multiple Model Fuzzy Control: Rancangan dan Simulasi Pada Tower Crane
on
D-007
Prosiding Conference on Smart-Green Technology in Electrical and Information Systems
Bali, 14-15 November 2013
Multiple Model Fuzzy Control:
Rancangan dan Simulasi Pada Tower Crane
Hendra Tjahyadi
Jurusan Sistem Komputer Universitas Pelita Harapan Tangerang, Indonesia hendra.tjahyadi@uph.edu
Abstrak—Untuk meningkatkan performansi respon transient dari sistemtower crane yang memiliki tingkat non-linearitas dan faktor ketidakpastian yang tinggi, sebuah pengontrol yang menggabungkan metoda multiple model dan logika fuzzy telah dirancang dan disimulasikan. Pada metoda ini plant dibandingkan dengan beberapa fuzzy model dalam sebuah bank model. Sebuah supervisor selanjutnya akanmengidentifikasi model mana yang terdekat dengan kondisi dari plant pada saat tersebut, dan akan mengaktifkan pengontrol yang terkait dengan model yang terpilih sehingga responstransient yang cepat dapat dicapai. Simulasi pada sistem tower crane menunjukkan multiple model fuzzy control yang dirancang menghasilkan respon yang lebih baik dari fuzzy control konvensional yaitu menghasilkan simpangan beban yang lebih kecil.
Keywords—multiple model; kontroller fuzzy; respon transient; tower crane, non-linear.
Mengontrol sistem non-linear merupakan tugas yang tidak mudah dilakukan. Kesulitan muncul karena beberapa faktor diantaranya adalah daerah kerja yang luas, non-linearitas yang besar (hard nonlinearity) dan ketidakpastian model [1]. Pengontrol yang didesain berdasarkan model linear dengan asumsi bahwa model yang akurat bisa diperoleh pada umumnya akan gagal memberikan unjuk kerja yang baik pada sistem non-linear, terkecuali pada daerah kerja yang sangat terbatas.
Ada beberapa metoda yang umum dipakai dalam mengontrol sistem non-linear seperti: gain scheduling control [2], adaptive control [3], robust control [4], neural network control [5] dan fuzzy control[6]. Fuzzy controlmenjadi pilihan yang menarik karena tidak memerlukan model matematika yang kompleks dalam proses desainnya, tetapi lebih berdasarkan kepada pengalaman seorang pakar yang dinyatakan dalam variable linguistic sehingga disebut sebagai desain dengan pendekatan pakar [7].
Untuk sistem dengan tingkat non-linearitas dan ketidakpastian yang besar penggunaan fuzzy control konvensional seringkali tidak memberikan performansi yang optimal. Hal ini terutama dikarenakan kesulitan untuk menentukan fungsi keanggotaan dari fuzzy control yang bisa mencakup daerah yang luas dengan ketidakpastian yang besar.
Untuk meningkatkan performansi dari fuzzy control dalammengontrol sistem dengan non-linearitas dan
Torang Simamora Project engineer S.C. Johnson Surabaya, Indonesia TSimamor@scj.com
ketidakpastian yang besar, sebuah pengontrol yang menggabungkan fuzzy control dengan multiple model control diusulkan pada paper ini. Di sini fuzzy model dibagi menjadi beberapa model dengan jalan membagi daerah kerjanya menjadi beberapa bagian.Untuk masing-masing model didesain sebuah fuzzy controller terkait. Selanjutnya, pada setiap saat sistem akan membandingkan semua model dengan plant yang dikontrol. Hasil pembandingan tersebut akan diteruskan pada sebuah supervisor yang akan menentukan model yang terdekat dengan plant yang dikontrol. Informasi tersebut selanjutnya dipakai untuk memilih pengontrol yang terkait dengan model terpilih untuk mengontrol plant pada saat tersebut. Dengan cara seperti itu diharapkan respontransient dari sistem akan meningkat karena plant akan dikontrol oleh pengontrol yang tepat pada setiap saat.
Untuk mendemonstrasikan metoda yang diusulkan dipilih sebuah tower crane sebagai plant yang akan dikontrol. Tower crane dipilih karena mempunyai tingkat non-linearitas yang tinggi dan mempunyai ketidakpastian yang besar akibat perubahan beban yang dipindahkan.
Pembahasan selanjutnya dari paper ini adalah sebagai berikut: Pada bagian II akan diberikan model dari tower crane yang menjadi plant yang akan dikontrol, selanjutnya bagian III akan mengulas mengenai metoda multiple model dan fuzzy control. Bagian IV akan berisi rancangan dan simulasi, dan akan ditutup dengan kesimpulan pada bagian V.
Tower crane merupakansuatu alat yang digunakan dalam industri untuk memindahkan beban yang berat dari satu tempat ke tempat lain yang berjauhan. Tower crane mengakomodasi pemindahan barang melalui ketinggian, sehingga efisiensi proses bongkar muat barang/beban meningkat.
Pada dasarnya sebuah tower crane memiliki struktur yang kompleks. Gambar.1 menunjukkan model tower crane yang bentuknya sudah disederhanakan, dengan sebuah beban (m) digantung tali dengan panjang (L) di bawahsebuah trolley (M). Saat digerakkan sejauh (x), beban mengalami simpangan/ayunan terhadap garis vertikaldengansudut∅. Sedangkan sudut yang dibentuk ketika beban berputar dilambangkan sebagaiθ.
Model dinamik dari tower crane diperoleh sebagai berikut [8]:
model (M1,M2,...Mn) dengan daerah kerja yang lebih kecil sehingga
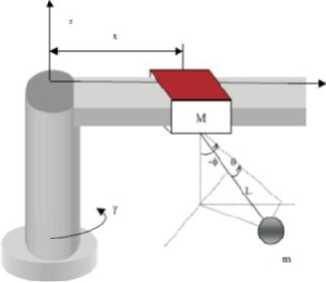
Gambar 1. Skematik Tower Crane
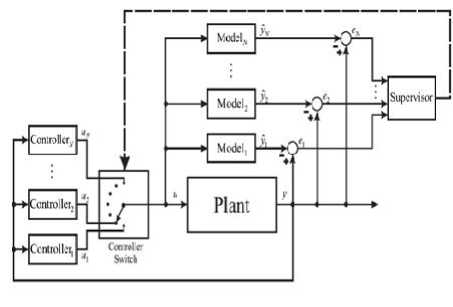
Gambar 2. Diagram Blok Dari Multiple Model Control
Mx + bxx + mgQ + Mxγ2 = Fx(I)
LQ + 2Lγθ - Ly2Q + Lγθ -X- xγ2 + gQ = 0 (2)
(J0 + Mx2)γ + bγγ - mgxQ + 2mxLγ2θ +
mL (xγ)Q + (m + 2M)xxγ = T(3)
Lθ - 2LγQ + gθ - Lγ2 - Lγ+ + xγ + xγ = 0 (4) dengan:
Fx = Besarnya gaya menggerakan trolley untuk memindahkan
beban (Newton)
T = Besarnya gaya untuk tower crane berotasi (Newton)
Q = Besarnya sudut yang dibentuk secara vertikal (radian)
= Besarnya sudut yang dibentuktower berotasi (radian )
= Besarnya sudut yang dibentuk ketika payload/beban berputar (radian)
x = Jarak yang sudah ditempuh trolley (meter)
g = Gravitasi bumi (m/.S' “ )
Dari persamaan dinamika yang ditunjukkan pada persamaan (1) – (4) jelas tampak tower crane merupakan suatu sistem yang non-linear.Kenon-linieran sistem mempersulit identifikasi sistemtowercrane dan mendesain sebuah pengontrol yang cocok untuk setiap keadaan yang dialami oleh tower crane agar lebih cepat dalam proses memindahkan beban.
Multiple Model Control
Multiple Model Control (MMC) merupakan suatumetode kontrol yang dipakai untuk mengatasi non-linearitas dan perubahan parameter plant.
Arsitektur dari MMC ditunjukkan pada Gambar 2 [9].Dalam metoda ini, plant yang memiliki daerah kerja dannon-linearitas yang besar dibagi menjadi menjadi beberapa
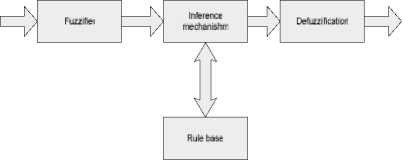
Gambar 3. Struktur Fuzzy Controller
faktor non-linearitas juga akan berkurang. Untuk masing-masing model, Mi, didesain sebuah pengontrol, Ci, yang secara relatif lebih mudah didesain. Kemudian sebuah mekanisme pemilih yang disebut sebagai supervisor akan memilih pengontrol yang tepat untuk mendapatkan respon yang diinginkan.
Supervisor bekerja dengan membandingkan error (e1,e2,..en) yang merupakan selisih antara output plant dan output setiap model. Supervisorakan mengidentifikasi model mana yang menghasilkan error terkecil selama periode waktu tertentu,dan memilih pengontrol yang paling sesuai untuk kondisi plant pada setiap waktu melalui mekanisme switching.
Fuzzy Control
Fuzzy logic controller merupakan sistem fuzzy yang diaplikasikan sebagai pengontrol. Variabel input pada pengontrol berupa selisih antara nilai referensi dengan nilai output yang disebut sebagai error. Sedangkan output fuzzy controller adalah sinyal kontrol yang menjadi masukan bagi aktuator.
Struktur fuzzy controllersecara umum dapat digambarkan seperti pada Gambar 3. Bagian pertama disebut Fuzzier yang akan melakukan fuzifikasi terhadap nilai variabel input, ini dilakukan dengan cara mengubah nilai input fuzzy yang umumnya berupa suatu angka diubah kedalam besaran fuzzy.Rule-base berisi aturan–aturan yang menggambarkan mekanisme proses kontrol dan menjadi acuan dalam memutuskan suatu nilai output sebagai respon atas input yang masuk ke sistem fuzzy. Bagian mesin inferensi berfungsi
mengambil kesimpulan atas nilai input yang ada berdasarkan aturan-aturan pada rule-base. Bagian akhir berupa defuzzification berfungsi melakukan pemetaan ruang aksi kontrol fuzzy yang didefenisikan pada semesta keluaran berupa nilai tertentu dari pada domain fuzzy.
Dalam paper ini fuzzy controller direalisasikan dengan menggunakan bantuan Fuzzy Inference System (FIS) pada MATLAB. FIS adalah sistem yang menggunakan metode fuzzy logic untuk memetakan input yang ada terhadap outputyang akan dihasilkan, sehingga menghasilkan suatu nilai outputyang diinginkan.
Langkah pertama perancangan adalah memodelkan tower crane berdasarkan persamaan (1) – (4).Parameter yang dipilih untuk dimanipulasi dalam simulasi adalah massa trolley (M), panjang tali (L), massa beban (m). Variabel yang dipilih sebagai variabel yang dikontrol adalah jarak yang ditempuh trolley (x), besarnya sudut simpangan secara vertikal (∅), besarnya sudut beban berputar (θ), kecepatan dari trolley (v).
Pada paper ini, kompleksitas dari sistem dibatasi dengan mengambil asumsi-asumsi berikut:
-
1. Massa dari lengan tower crane diabaikan.
-
2. Simpangan yang dialami oleh beban kecil, θ dan ∅ ≤ 5o
-
3. Massa dari tali yang digunakan diabaikan.
-
4. Jarak maksimum yang ditempuh oleh trolley dibatasi yaitu sebesar 20 meter.
-
5. Kecepatan maksimum crane adalah 0,4 m/s
-
6. Tower crane tidak dalam keadaan berputar atau melakukan rotasi (T = 0).
Spesifikasi tower crane dipakai dalam pemodelan dan simulasi dibuat mendekati nilai real dari komponen tower crane yang biasa digunakan dan ditunjukkan pada Tabel.1
Selanjutnya, jarak tempuh trolley maksimum sebesar 20 meter dibagi menjadi tiga daerah kerja dengan jalan melinearisasi model pada jarak 3 meter, 10 meter dan 18 meter untuk mendapatkan tiga buah model yang dinyatakan dalam bentuk state-space. Model linear tersebut diperoleh dengan jalan melinearisasi model non-linear yang dibangun di dalam SIMULINK dengan menggunakan perintah linmod pada MATLAB. Model akan memiliki 8 variabel statex1 – x8 yang masing-masing secara berurutan adalah X,∅, γ,θ,ẏ, )̇, ∅̇ , ḟ. Titik-titik linearisasi untuk model 1 sampai model 3 ditunjukkan pada Tabel 2, harga F dan m untuk semua model adalah sama yaitu 100 N dan 1000 Kg.
Dengan memasukkan harga-harga tersebut pada perintah linmod maka akan diperoleh matriks state spacedari masing-masing model M1 – M3.
Setelah model linear dibangun selanjutnya adalah mendesain fuzzy controller.Hal pertama yang dilakukan untuk mendesain fuzzy controller adalah menentukan variabel input dan variabel outputpada MATLAB dengan menggunakan FIS editorseperti ditunjukkan pada Gambar 4.
Gambar4 menjelaskan bahwa variabel input untuk mengendalikan crane adalah jarak yang ditempuh (x), besarnya sudut simpangan vertikal yang dialami oleh beban (∅), dan kecepatan crane (v). Sedangkan output-nya adalah besarnya
Tabel 1.Spesifikasi model Tower Crane
|
No |
Variabel |
Harga |
|
1 |
Massa toley (M) |
400 Kg |
|
2 |
Massa Beban (m) |
1000 Kg |
|
3 |
Panjang tali (L) |
50 m |
|
4 |
Koefisien gesekan trolley (bx) |
2,65 |
|
5 |
Momen Inersia tower (J0) |
50 Kgm2 |
|
6 |
Koefisien gesekan tower (b ) |
2,65 |
Tabel 2. Titik-titik linearisasi untuk mendapatkan model linear M1 – M3.
|
Model |
∅ |
^ |
5-2 |
* |
̇ |
• ∅̇ | ||
|
M1 |
3 |
5 |
0 |
3 |
0,15 |
0 |
0 |
0 |
|
M2 |
10 |
5 |
0 |
3 |
0,40 |
0 |
0 |
0 |
|
M3 |
18 |
5 |
0 |
3 |
0,2 |
0 |
0 |
0 |
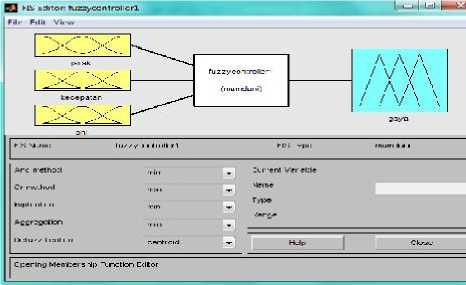
Gambar 4. FIS editor untuk variabel input dan output
(c) (d)
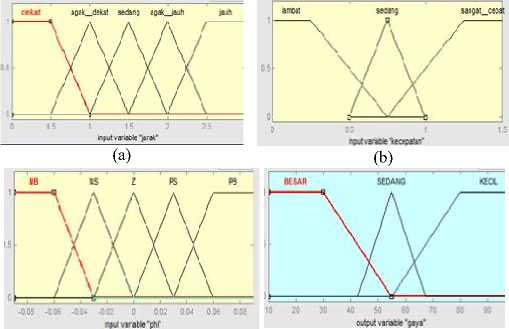
Gambar 5.Fungsi keanggotaan input dan outputfuzzy controller pada sistem tower crane. (a) inputx, (b)input v, (c) input ∅, (d) output F.
gaya (F).Fungsi keanggotaan yang digunakan untuk masing -masing variabel ditunjukkan pada Gambar 5. Jarak yangditempuh (x) dibagi dalam lima nilai lingustik yaitu dekat, agak dekat, sedang, agak jauh dan jauh, kecepatan crane (v)
dibagidalam tiga nilai lingustik yaitu lambat, sedang dan cepat, besarnya sudut simpangan (∅), dibagi dalam 5 nilai lingustik yaitu Negative Big (NB), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Big (PB).
Setelah membuat partisi fuzzy dan memilih fungsi keanggotaan untuk masing – masing variabel input dan output, proses berikutnya adalah menentukan aturan – aturan kontrolfuzzy (rule base). Tipe fuzzy controller yang digunakan pada paper ini adalah tipe Mamdani karena lebih tepat digunakan untuk model plant yang tidak diketahui secara pasti, tetapi terdapat operator atau pakar yang mengetahui karakteristik sistem yang dikontrol. Aturan kontrolfuzzy yang dirancang berdasarkan pengetahuan engineer atau operator yang diekspresikan dalam bentuk implikasi fuzzy yaitu aturan IF – THEN. Diperoleh 60 aturan untuk fuzzy controller yang akan direalisasikan, beberapa diantaranya disampaikan di bawah ini sebagai contoh, pembaca diminta mengacu pada [10] untuk aturan selengkapnya.
-
1. If (jarak is dekat) and (kecepatan is lambat) and (phi is NB) then (gaya is CEPAT) (1)
-
2. If (jarak is dekat) and (kecepatan is lambat) and (phi is NS) then (gaya is CEPAT) (1)
-
3. If (jarak is dekat) and (kecepatan is lambat) and (phi is Z) then (gaya is LAMBAT) (1)
-
4. If (jarak is dekat) and (kecepatan is lambat) and (phi is PS) then (gaya is SEDANG) (1)
-
5. If (jarak is dekat) and (kecepatan is lambat) and (phi is PB) then (gaya is LAMBAT) (1)
-
6. If (jarak is dekat) and (kecepatan is sedang) and (phi is NB) then (gaya is CEPAT) (1)
-
7. If (jarak is dekat) and (kecepatan is sedang) and (phi is NS) then (gaya is SEDANG) (1)
-
8. If (jarak is dekat) and (kecepatan is sedang) and (phi is Z) then (gaya is LAMBAT) (1)
-
9. If (jarak is dekat) and (kecepatan is sedang) and (phi is PS) then (gaya is SEDANG) (1)
-
10. If (jarak is dekat) and (kecepatan is sedang) and (phi is PB) then (gaya is LAMBAT) (1)
Metoda defuzzifikasi yang digunakan yaitu center of area (COA) pada MATLAB dipilih centroid. Metoda COA diyakini lebih baik dalam menghasilkan kondisi respon transient. Selanjutnya fuzzy controller yang dirancang akan di-cluster untuk masing- masing model. Model diasumsikan sebagai fuzzy set untuk membuat batasan – batasan daerah kerja dari masing – masing fuzzy controller yang digunakan, sehingga fuzzylogiccontroller tidak bekerja untuk keseluruhan sistem, tetapi akan bekerja pada saat keadaan-keadaan(cluster) tertentu yang sudah ditentukan.
Proses selanjutnya adalah membuat supervisor yang digunakan memilih model yang memberikan pendekatan terbaik untuk kondisi plantsaat bekerja. Supervisor akan melakukan perhitungan terhadap setiap error dari masing – masing model dan membandingkannya untuk medapatkan error mana yang paling kecil yang akan digunakan memberitahu switch untuk mengaktifkan pengontrol yang tepat.
Setelah semua tahapan dilalui maka multiple model fuzzy control untuk tower crane diimplemantasikan dalam SIMULINK. Diagram blok dari keseluruhan sistem ditunjukkan pada Gambar 6.
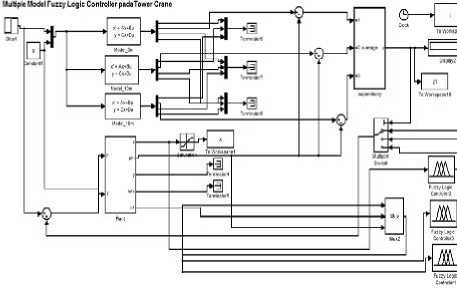
Gambar 6. Diagram blok multiple model fuzzy control
Ada dua simulasi yang akan ditampilkan dalam paper ini. Simulasi pertama adalah kasus dimana terjadi pengurangan massa beban yang dibawa saat crane bergerak dari titik awal menuju titik akhir. Sedangkan simulasi kedua merupakan kasus dimana terjadi penambahan massa beban yang dibawa crane saat crane bergerak dari titik awal menuju titik akhir. Penambahan atau pengurangan massa beban bisa terjadi misalnya saja diakibatkan oleh perubahan besar angin yang menekan beban ke atas atau ke bawah sehingga crane akan melihat hal itu sebagai pengurangan atau penambahan massa beban. Untuk kasus pengurangan massa beban bisa juga terjadi karena misalnya ada bagian dari massa yang terlepas atau terjatuh dari crane.
Untuk kedua simulasi ini besarnya gaya yang diterapkan adalah sebesar 80 N dan jarak yang harus ditempuh adalah sebesar 20 meter. Variabel yang menjadi pengamatan adalah besarnya sudut simpangan, ∅. Akan dibandingkan respon sistem yang dikontrol oleh fuzzy control konvensional dengan yang dikontrol oleh multiple model fuzzy control. Untuk multiple model fuzzy controlakan ditunjukkan diagram switching yang menunjukkan bagaimana sistem memilih model yang berbeda agar bisa mendapatkan respon yang lebih baik.
Simulasi pertama
Pada simulasi inimassa beban yang dibawa oleh crane berubah dari 1000 Kg pada saat t = 0 detik menjadi 800 Kg pada saat t = 16 detik dan berubah menjadi 700 Kg pada saat t = 32 detik. Respon simpangan sistem ditunjukkan pada Gambar 7 dan diagram switchingdari sistem ditunjukkan pada Gambar 8.
ι<w'
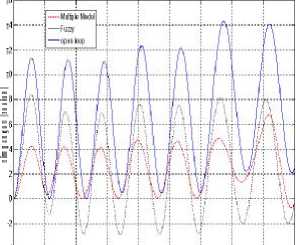
Gambar 7. Respon sudut simpangan untuk perubahan beban dari
m=1000 kg ÷800 kg÷ 700 kg
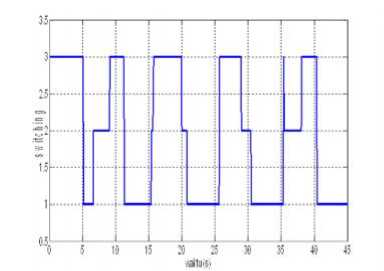
Gambar 8. Diagram switching untuk perubahan beban dari m=1000 kg ÷800 kg÷ 700 kg dengan F=80 N.
Dari Gambar 7 terlihat simpangan beban (0)maksimum saat sistem tidak dikontrol adalah sebesar 0.014 radian. Simpangan ini diperbaiki menjadi maksimumsebesar 0.008radian dengan menggunakan fuzzy controller konvensional dan diperbaiki menjadi maksimum sebesar 0.006 radian dengan menggunakan multiple model fuzzy controller. Hal ini menunjukkan bahwa multiple model fuzzy controllermemberikan perbaikan respon terhadap open loop dan lebih baik dibandingkan hanya menggunakan satu fuzzy controller.Gambar 8 menunjukkan bagaimana model-model yang berbeda-beda dipilih oleh supervisor untuk dapat memberikan performansi yang lebih baik pada setiap saat terlepas dari adanya perubahan parameter sistem.
Simulasi kedua
Pada simulasi inimassa beban yang dibawa oleh crane berubah dari 1000 Kg pada saat t = 0 detik menjadi 1100 Kg pada saat t = 12 detik kemudian berubah menjadi 1200 Kg pada saat t = 24 detik dan kembali berubah menjadi 1300 Kg pada saat t = 36 detik. Respon simpangan sistem ditunjukkan pada Gambar 9 dan diagram switching dari sistem ditunjukkan pada Gambar 10.
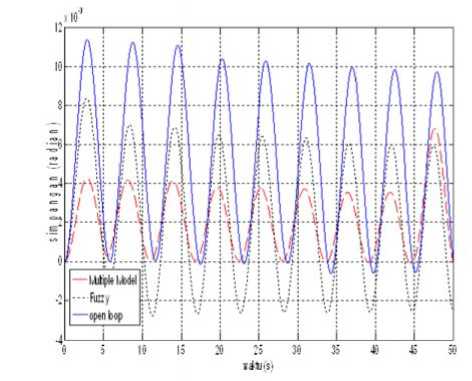
Gambar 9. Respon sudut simpangan untuk perubahan beban dari
m=1000 kg ÷1100 kg÷ 1200 kg÷ 1300 kg
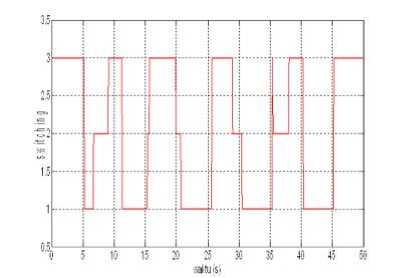
Gambar 10. Diagram switching untuk perubahan beban dari m=1000 kg
÷1100 kg÷ 1200 kg÷ 1300 kg
Seperti pada simulasi pertama saat beban berkurang, pada kasus penambahan beban multiple model fuzzy controller mampu memperbaiki respon yang diberikan oleh fuzzy control konvensional.Simpangan beban (0)maksimum saat sistem tidak dikontrol adalah sebesar 0.011 radian. Simpangan ini diperbaiki menjadi maksimumsebesar 0.008radian dengan menggunakan fuzzy controller konvensional dan diperbaiki menjadi maksimum sebesar 0.004 radian dengan menggunakan multiple model fuzzy controller. Gambar 10 menunjukkan perilaku yang serupa dengan Gambar 8.Terlihat bagaimana supervisor berpindah memilih model yang berbeda saat crane berpindah dari satu tempat ke tempat yang lain dan mengalami perubahan beban.
Kombinasi antara prinsip multiple model dan fuzzy control terbukti berhasil meningkatkan performansi sistem dengan memperbaiki renspon transient untuk sistem dengan non-linearitas dan ketidakpastian yang tinggi. Hal ini dibuktikan berdasarkan hasil simulasi pada modeltower cranedengan ketidakpastian model yaitu perubahan massa beban, terlihat bahwa multiple modelfuzzy logic controllerdengan mekanisme
switching yang dimilikinya berhasil mengurangi besarnya simpangan pada beban (∅)dibandingkan fuzzy logic controller tanpa prinsip multiple model.
References
-
[1] Slotine, J.J.E., and Li, W. Applied Nonlinear Control, Prentice Hall, 1991.
-
[2] Garcia, S.J. et al., Modelling, simulation, and gain scheduling control of large radiotelescopes, Simulation Practice and Theory 8: 141-160, 2000.
-
[3] Sun Z., Liu Y., Adaptive state-feedback stabilization for a class of high-order nonlinear uncertain systems. Automatica, 43(10): 1772–1783, 2007.
-
[4] Mahdi Jalili, M. et al., Design of robust sub-optimal nonlinear Hinf controllerswith some applications,Communications in Nonlinear Science and Numerical Simulation 12: 1053–1067, 2007.
-
[5] Shafiq, M. and Butt, N.R., Utilizing Higher-Order Neural Networks in U-model Based Controllers for Stable Nonlinear Plants, Journal of Control, Automation, and Systems, 9(3):489-496, 2011.
-
[6] Abid, H. et al., An Indirect Model Reference Robust Fuzzy Adaptive Control for a Class of SISO Nonlinear Systems,International Journal of Control, Automation, and Systems, 7(6):982-991, 2009.
-
[7] Reznik, L., Fuzzy Controller, , Butterworth-Heinemann, 1997.
-
[8] Al-Mousa, A. A., Control of Rotary Cranes Using Fuzzy Logic and
Time-Delayed Position Feedback Control, Master Thesis, Virginia Polytechnic Institute and State University, 2000.
-
[9] Narendra, K.S. and Balakrishnan, J., “Adaptivecontrol using multiple models and switching,” IEEE Trans. Automat.Contr.,42: 171-187, 1997.
-
[10] Simamora, T. Desain dan Simulasi Multiple Model Fuzzy Logic Control pada Tower Crane, Tugas Akhir, Universitas Kristen Maranatha, Bandung, 2011.
232
ISBN: 978-602-7776-72-2 © Universitas Udayana2013
Discussion and feedback