ANALISIS KEPUTUSAN INVESTASI PADA SAHAM PERBANKAN MENGGUNAKAN CAPM DAN CAPM-MONTE CARLO
on
E-Jurnal Matematika Vol. 12(2), Mei 2023, pp. 155-161
DOI: https://doi.org/10.24843/MTK.2023.v12.i02.p413
ISSN: 2303-1751
ANALISIS KEPUTUSAN INVESTASI PADA SAHAM PERBANKAN MENGGUNAKAN CAPM DAN CAPM-MONTE CARLO
Emerald Diori Silaban1§, Komang Dharmawan2, Desak Putu Eka Nilakusmawati3
1Program Studi Matematika, FMIPA, Universitas Udayana [Email: emeralddiori88@gmail.com]
2Program Studi Matematika, FMIPA, Universitas Udayana [Email: k.dharmawan@unud.ac.id]
3Program Studi Matematika, FMIPA, Universitas Udayana [Email: nilakusmawati@unud.ac.id]
§Corresponding Author
ABSTRACT
This research purpose is to calculate value of beta and expected return on CAPM using historical data and using data from Monte Carlo simulations. The data used in this research is stock data from the infobank index15. The model used in this study is the CAPM equilibrium model and to estimate the stock price this research uses a Monte Carlo simulation. The results showed that beta calculations used historical data and simulated data on BBCA stocks (0,91578 and 0,89393), BBNI (2,10434 and 2,28636), BBRI (1,42862 and 1,43427), BMRI (1,28249 and 1,37485), and BBTN (2,49935 and 2,75265). With these results, BBCA stock is defensive because the beta is less than one and the other four stocks are aggressive because the beta is more than one. The expected return calculation results using historical data and simulation data are BBCA (5,42% and 5,28%), BBNI (6,46% and 8,05%), BBRI (5,87% and 6,36%), BMRI (5,74% and 6,24%), and BBTN (6,81% and 8,98%).
Keywords: beta, expected return, monte carlo simulation
sederhana dalam menggambarkan hubungan risiko dan return juga hanya menggunkan satu variabel (beta) dalam menunjukkan risiko, sedangkan model APT lebih kompleks karena menggunakan beberapa variabel pengukur risiko untuk risiko juga return. APT pada dasarnya mengemukakan jikalau expected return dari suatu sekuritas bisa
dipengaruhi oleh banyak sumber risiko lain dan beta saja belumlah cukup.
Beta merupakan suatu risiko sistematis, risiko yang pasti ada dan tidak dapat dihilangkan melalui cara diversifikasi karena naik turunnya risiko ini dipengaruhi oleh faktor-faktor makro yang bisa memengaruhi pasar, seperti perubahan tingkat suku bunga, kurs valas, dan kebijakan pemerintah. Menentukan expected return juga meminimalkan risiko investasi merupakan tujuan CAPM.
Penggunaan data historis seringkali kurang memberikan gambaran sesungguhnya situasi pada masa depan oleh sebab itu maka dipandang perlu
untuk melakukan estimasi atau prediksi tentang data yang akan dipakai dalam pengambilan keputusan. Salah satu metode yang saat ini sering dipakai mensimulasi pergerakan harga saham adalah simulasi Monte Carlo. Sebelum menggunakan CAPM, penulis akan mencari beta menggunakan Simulasi Monte Carlo.
Simulasi Monte Carlo adalah suatu metode yang melibatkan pembangkitan bilangan acak dengan distribusi probabilitas yang dapat diketahui dan ditentukan.. Oleh sebab itu Simulasi Monte Carlo digunakan untuk mencari return saham yang dipilih (dalam hal ini prediksi pergerakan saham). Simulasi Monte Carlo digunakan untuk mencari nilai beta. Setelah nilai beta didapatkan, dilanjutkan dengan perhitungan menggunakan model CAPM.
Penelitian sebelumnya oleh Safira, dkk. (2021) membandingkan hasil expected return dari CAPM menggunakan GBG dan CAPM historis dan juga penelitian oleh Ameliyah, dkk. (2017) membandingkan perhitungan beta CAPM menggunakan GARCH dan EGARCH. Pada kedua penelitian itu sama-sama dicari perbandingan hasil CAPM baik itu beta maupun expected return menggunakan data historis dengan peramalan atau simulasi lain. Maka dengan itu penulis membuat penelitian analisis keputusan pada saham perbankan menggunakan CAPM dan CAPM-Monte Carlo.
Apalagi saham i. akan dihitung σ return-nya, maka variance Ri dapat diformulasikan, sebagai berikut: T
σι=⅛∑(Rtt- Ri )2 (2)
t = 1
dan standar deviasi Rt adalah
Oi =
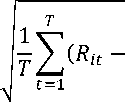
R1 )2
(3)
CAPM
Pembahasan mengenai CAPM bisa menunjukkan saham yang efisien dengan melihat apakah selisih nilai return sebenarnya dengan nilai expected return CAPM bernilai positif atau negatif oleh Liadi, dkk (2020).
Model CAPM sering dinamakan Garis Pasar Modal (Security Market Line, SML), Sharpe mengembangkannya pada 1995. (Sharpe, 1995) SML adalah garis yang menunjukkan hubungan antara risiko (diukur oleh beta) dengan return (R) dan garis tersebut adalah garis yang linear. Maka formulasinya adalah:
Return
“Return adalah pendapatan yang dinyatakan dalam persentase dari modal awal investasi. Pendapatan investasi dalam saham ini merupakan keuntungan yang diperoleh dari jual-beli saham, dimana jika mendapat untung disebut capital gain dan jika rugi disebut capital loss” (Samsul, 2006). Return dapat dinyatakan sebagai berikut:
d _ St+1— St
Rt~~ST~
(1)
E(Rt) = Rf+ (Rm - Rf)βl (4)
dengan E(Ri) adalah expected return saham, Rf return bebas risiko, Rm adalah return pasar, βi adalah risiko suatu saham dan (Rm — Rf)βi adalah premi risiko.
Beta adalah pengukur volatilitas (volatility) return suatu sekuritas terhadap return pasar. Beta menggambarkan hubungan (gerakan) antara saham dan pasarnya (saham secara keseluruhan). Pada pembahasan CAPM, beta diartikan sebagai risiko sistematis saham. Pertama dicari dahulu nilai kovarian return saham dan return pasar. Setelah itu varian dari return pasar. Dengan rumus seperti dibawah ini:
dengan St merupakan harga saham saat periode ke-1 , St+1 merupakan harga saham saat periode ke-t + 1 ,dan Rt merupakan tingkat keuntungan (return) saham periode ke-t.
Cov (Ri,RM)
X(Ri - Ri)(RM - RM) N — 1
(5)
Risiko
Teori statistik memberi ukuran penyimpangan yang disebut deviasi standar (σ) atau pada bentuk kuadrat dinyatakan sebagai variance (σ2).
Var (Rm)
∑(RM — rm)2
N — 1
(6)
Adapun cara untuk mengukur beta adalah:
Berikut ini langkah analisis data yang dilakukan:
Cov (RM l Var (Rm)
(7)
-
1. Mengumpulkan data saham yang termasuk pada indeks infobank15 dan memilih 5 perusahaan terbesar.
-
2. Menghitung return aset saham dan return pasar.
βi = βi= (8)
^m
Simulasi Monte Carlo
Simulasi Monte Carlo mempunyai istilah lain yaitu sampling simulation atau Monte Carlo Sampling Technique. Sering juga dipakai dalam evaluasi hasil dari transformasi input dan risiko pada pengambilan keputusan menggunakan data sampling yang sudah ada (historical data) dan sudah diketahui penyebaran datanya atau dengan kata lain pada simulasi ini harus ada elemen faktor kemungkinan maka simulasi bisa berjalan (Kakiay, 2004). Pembangkitan bilangan random adalah dasar dari metode ini.
Mengestimasi harga saham dimasa depan dengan rumus:
Rt
St+i — St St
-
3. Menghitung nilai beta.
(1)
Cov (RM βl Var (Rm)
(7)
-
4. Menghitung nilai expected return CAPM.
E(Rι) = Rf+ (Rm - Rf)βl
(4)
-
5. Selanjutnya adalah perhitungan menggunakan data simulasi Monte Carlo. Tahapan
mengestimasi nilai saham menggunakan simulasi Monte Carlo adalah sebagai berikut: a) Mencari nilai standar deviasi saham,
St = So exp
[(μ + 2σ2)∆t + √tσεf]
(9)
dengan St merupakan harga saham saat periode ke-1 , S0 merupakan harga saham awal dan σ merupakan standar deviasi.
σι =
J t=i
-
Ri )2
(10)
b) setelah itu mencari volatility saham dengan cara,
σ = σi x √τ
(11)
c) Melakukan simulasi dengan menggunakan rumus dibawah ini dan juga melaksanakan simulasi berjumlah 1000 kali.
St
= S0 exp [(μ + - σ2) Δt + √tσεl]
(9)
-
6. Setelah harga saham diestimasi, langkah yang sama untuk perhitungan CAPM pada data historis juga dilakukan juga dilakukan pada perhitungan menggunakan data simulasi.
Pertama akan dicari nilai return. Perhitungan return saham BBCA akan digunakan sebagai contoh dengan nilai saham pada Januari 2017 senilai 2.804,91 dan Februari 2017 senilai 2.832,41, maka berdasarkan persamaan (1) perhitungan return BBCA adalah:
Ri
2.832,41 - 2.804,91
2.804,91
0,009804
Setelah dihitung satu-persatu selanjutnya adalah nilai dari setiap return tersebut dihitung rata-rata
perbulan lalu return tahunannya seperti pada Tabel 1.
Tabel 1. Return Bulanan dan Tahunan
|
Saham |
Return Bulanan |
Return Tahunan |
|
BBCA |
0,018535 |
0,222417 |
|
BBNI |
0,012359 |
0,148307 |
|
BBRI |
0,015124 |
0,181487 |
|
BMRI |
0,010524 |
0,126282 |
|
BBTN |
0,012420 |
0,149040 |
|
JKSE |
0,004576 |
0,054914 |
Setelah nilai return, dilanjutkan dengan perhitungan nilai beta tiap saham. Sebelumnya dicari dahulu nilai kovarian antara saham dan pasar lalu nilai varian pasar. Sebelumnya nilai varian pasar adalah 0,001731. Dapat dilihat pada Tabel 2 nilai kovarian dan beta saham.
Tabel 2. Kovarian dan Beta Data Historis
|
Saham(i) |
σiM |
β, = σ⅛-σM |
|
BBCA |
0,001586 |
0,915779 |
|
BBNI |
0,003644 |
2,104338 |
|
BBRI |
0,002474 |
1,428616 |
|
BMRI |
0,002221 |
1,282492 |
|
BBTN |
0,004327 |
2,499350 |
Perhitungan expected return menggunakan saham BBCA sebagai contoh adalah berikut ini: Pada variabel return dan risiko terdapat komponen tingkat suku bunga bebas risiko (Rf) dengan rata-rata pada 5 tahun adalah 4,61%.
Rf = 0,0461
Rm = 0,054914 βi = 0,915779
Maka, dapat dicari nilai expected return dari saham BBCA:
E(Ri) = 0,0461 + (0,054914 - 0,0461) x 0,915779
E(Ri) = 0,054172
Berikut ini merupakan hasil perhitungan nilai expected return pada kelima saham:
Tabel 3. Expected Return Data Historis
|
Saham(i) |
βi |
E(Ri) (%) |
|
BBCA |
0,915779 |
5,41% |
|
BBNI |
2,104338 |
6,46% |
|
BBRI |
1,428616 |
5,87% |
|
BMRI |
1,282492 |
5,74% |
|
BBTN |
2,499350 |
6,81% |
-
3.2 Proses CAPM Berdasarkan Data Simulasi
Monte Carlo
Simulasi Monte Carlo akan dipakai untuk mencari harga saham kedepan. Setelah itu bisa dicari return dari masing-masing saham. Lalu beta saham dapat dihitung dan dilanjutkan ke perhitungan CAPM.
Berikut ini merupakan proses perhitungan varians, standar deviasi, dan annual volatility setiap saham untuk return yang dipakai adalah nilai yang sudah didapatkan dari perhitungan menggunakan data historis sebelumnya, diketahui bahwa varian BBCA adalah 0,002825, maka dapat dicari standar deviasi:
σi = √0,002825
σi = 0,053151
Selanjutnya nilai dari volatility adalah:
σ = 0,053151 x √12
σ = 0,18412
Tabel 4. Varian, Standar Deviasi, dan Volatility
|
Saham |
Varian |
Stadar Deviasi |
Volatility |
|
BBCA |
0,002825 |
0,053151 |
0,18412 |
|
BBNI |
0,012791 |
0,113099 |
0,39179 |
|
BBRI |
0,006148 |
0,078406 |
0,27161 |
|
BMRI |
0,005653 |
0,075184 |
0,26045 |
|
BBTN |
0,026208 |
0,161889 |
0,56080 |
|
JKSE |
0,001731 |
0,041611 |
0,14414 |
Setelah annual volatility diestimasi,
berikutnya adalah menggunakan nilai expected return dari perhitungan menggunakan data
historis sebelumnya untuk nilai μ. Selanjutnya dapat dimulai perhitungan simulasi Monte Carlo dengan rumus:
St = S0 exp [(μ + -σ2)∆t + √tσεi]
Setelah harga saham disimulasi maka dapat dicari nilai return setiap saham. Berikut ini merupakan nilai return setiap saham:
Tabel 5. Return Bulanan dan Tahunan
|
Saham |
Return Bulanan |
Return Tahunan |
|
BBCA |
0,018535 |
0,222416 |
|
BBNI |
0,012360 |
0,148314 |
|
BBRI |
0,015122 |
0,181470 |
|
BMRI |
0,010531 |
0,126367 |
|
BBTN |
0,012409 |
0,148905 |
|
JKSE |
0,004576 |
0,054909 |
Selanjutnya adalah perhitungan beta juga menggunakan data dari simulasi Monte Carlo sebelumnya. Nilai varian pasar adalah 0,001820016. Berikut ini merupakan hasil
perhitungan kovarian antar saham dan beta pada setiap saham:
Tabel 6. Kovarian dan Beta Data Simulasi
|
Saham(i) |
σfM |
βι = σfM σM |
|
BBCA |
0,001627 |
0,893934 |
|
BBNI |
0,004161 |
2,286358 |
|
BBRI |
0,002610 |
1,434271 |
|
BMRI |
0,002502 |
1,374850 |
|
BBTN |
0,005010 |
2,752645 |
Selanjutnya adalah perhitungan expected return dengan contoh menggunakan saham BBCA. Risk free rate yang dipakai adalah nilai yang terbaru pada data yaitu pada Desember 2021 sebesar 3,50%.
Rf = 0,0350
Rm = 0,054909
βi = 0,893934
Maka, dapat dicari nilai expected return dari saham BBCA:
E(Rf) = 0,0350 + (0,054909 - 0,0350) x 0,893934
E(Rf) = 0,054172
Berikut ini merupakan hasil perhitungan expected return saham lainnya:
Tabel 7. Expected Return Data Simulasi
|
Saham(i) |
βt |
E(Rf) (%) |
|
BBCA |
0,893934 |
5,28% |
|
BBNI |
2,286358 |
8,05% |
|
BBRI |
1,434271 |
6,36% |
|
BMRI |
1,374850 |
6,24% |
|
BBTN |
2,752645 |
8,98% |
-
3.3 Perbandingan Hasil Perhitungan CAPM Menggunakan Data Historis Dan Data Simulasi
Tabel 8. Perbandingan hasil perhitungan CAPM data historis dan data simulasi
|
Kode Saham |
Beta |
Expected Return (%) | ||
|
Data Historis |
Data Simulasi |
Data Historis |
Data Simulasi | |
|
BBCA |
0,91578 |
0,89393 |
5,42% |
5,28% |
|
BBNI |
2,10434 |
2,28636 |
6,46% |
8,05% |
|
BBRI |
1,42862 |
1,43427 |
5,87% |
6,36% |
|
BMRI |
1,28249 |
1,37485 |
5,74% |
6,24% |
|
BBTN |
2,49935 |
2,75265 |
6,81% |
8,98% |
Tabel 8 menunjukkan bahwa berdasarkan nilai beta, saham BBTN merupakan saham yang memiliki risiko tertinggi dengan perhitungan menggunakan data historis dan data simulasi yaitu 2,49935 dan 2,75265. Nilai beta saham BBCA pada data historis dan data simulasi bernilai lebih kecil dari satu yaitu 0,91578 dan 0,89393. Hal ini menunjukkan bahwa saham BBCA bersifat defensif yang menggambarkan bahwa nilai saham tidak gampang berubah berdasarkan kondisi pasar. Sedangkan pada keempat saham lainnya dengan perhitungan menggunakan data historis dan data simulasi memiliki nilai beta lebih besar dari satu. Dengan kondisi beta saham lebih dari satu maka saham BBNI, BBRI, BBCA, dan BBTN bersifat agresif yang menggambarkan keadaan harga saham cenderung lebih gampang berubah berdasarkan kondisi pasar dan risiko lebih tinggi. Pada Tabel 8 dapat dilihat bahwa hubungan antara beta dan expected return berdasarkan data historis dan data simulasi bersifat linier atau searah.
Pada perhitungan menggunakan data historis didapatkan nilai beta saham BBCA sebesar 0,91578 dan pada perhitungan menggunakan data dari simulasi Monte Carlo didapatkan sebesar 0,89393. Berdasarkan kedua hasil itu beta saham BBCA lebih kecil dari satu, sehingga saham BBCA bersifat defensif yang menggambarkan bahwa nilai saham tidak gampang berubah berdasarkan kondisi pasar. Sedangkan hasil perhitungan menggunakan data historis dan data simulasi pada beta saham BBNI (2,10434 dan 2,28636 ), BBRI (1,42862 dan 1,43427), BMRI (1,28249 dan 1,37485), dan BBTN (2,49935 dan 2,75265) lebih besar dari satu. Maka saham BBNI,
BBRI, BMRI, dan BBTN bersifat agresif yang menggambarkan keadaan harga saham cenderung lebih gampang berubah berdasarkan harga pasar dan risiko lebih tinggi.
Hasil perhitungan expected return CAPM menggunakan data historis adalah BBCA (5,42%), BBNI (6,46%), BBRI (5,87%), BMRI (5,74%),dan BBTN (6,81%). Sedangkan hasil perhitungan expected return dengan menggunakan data dari simulasi Monte Carlo adalah BBCA (5,28%), BBNI (8,05%), BBRI (6,36%), BMRI (6,24%), dan BBTN (8,98%). Berdasarkan hasil perhitungan expected return pada masing-masing saham dengan menggunakan data historis dan data simulasi Monte Carlo selisih hasil perhitungan expected return nilainya tidak terlalu besar.
Saran yang dapat penulis berikan berdasarkan penelitian yang sudah dilakukan: (1) Bagi penelitian selanjutnya, pada proses perhitungan prediksi harga saham menggunakan simulasi Monte Carlo dapat ditambahkan lagi jumlah simulasi yang akan dieksekusi dan simulasi Monte Carlo dapat dihitung menggunakan software lainnya; (2) Menambahkan lagi jumlah sampel dan periode penelitian yang terbaru, agar perkembangan mengenai investasi saham terkini dapat diketahui; dan (3) Menggunakan metode keseimbangan yang lain seperti APT (Arbitrage Pricing Theory).
DAFTAR PUSTAKA
Ameliah, V., Dharmawan, K., & Widana, I. N.
-
(2017) . Membandingkan Risiko Sistematis Menggunakan CAPM-GARCH Dan CAPMEGARCH. E-Jurnal Matematika Vol.6, 241247.
Herlianto, D. (2013). Manajemen Investasi Plus Jurus Mendeteksi Investasi Bodong. Yogyakarta: Gosyen Publicing.
Kakiay, T. J. (2004). Pengantar Sistem Simulasi. Yogyakarta: Andi Offset.
Liadi, E., Dharmawan, K., & Nilakusmawati, D. P. (2020). Menentukan Saham Yang Efisien Dengan Menggunakan Capital Asset Pricing Method. E-Jurnal Matematika Vol.9(1), 2330.
Safira, I. W., Dharmawan, K., & Nilakusmawati, D.P.E. (2021). Penentuan Keputusan
Investasi Saham Menggunakan Capital Asset Pricing Model (CAPM) Dengan Penafsir Parameter Stokastik. E-Jurnal Matematika Vol.10(4), 251-257.
Samsul, M. (2006). Pasar Modal dan Manajemen Portofolio . Surabaya: Penerbit Erlangga.
Sharpe, W. F., Gordon, J. A., & Baily, V. (1995). Investment. New York: Prentice Hall.
161
Discussion and feedback