PEMILIHAN KRITERIA DALAM PEMBUATAN KARTU KREDIT DENGAN MENGGUNAKAN METODE FUZZY AHP
on
E-Jurnal Matematika Vol. 3, No.1 Januari 2014, 25-32
ISSN: 2303-1751
PEMILIHAN KRITERIA DALAM PEMBUATAN KARTU KREDIT DENGAN MENGGUNAKAN METODE FUZZY AHP
Joko Hadi Aprianto1, G. K. Gandhiadi2, Desak Putu Eka Nilakusmawati3
-
1,2,3Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: 1joko.hadi09@yahoo.com,2gandhiadigk@yahoo.com, 3nilakusmawati_desak@yahoo.com
Abstract
The rise of credit card users, make banks compete to provide a wide range of offers to attract customers. This study aims to determine the priority criteria selected customers for establishment credit cards by using a fuzzy AHP method. Method fuzzy AHP is a combination of the AHP method and fuzzy method. Fuzzy AHP approach particularly triangular fuzzy number approach to the AHP scale should be able to minimize uncertainty for the results obtained are more accurate. The criteria used for this study is the interest rate , the promo/discount, limit, and annual dues. Based on the steps of calculation of data obtained fuzzy AHP respondents have value CR = 0.049, which means consistent because it meets the standards set CR < 0.10 and that became the order of priority are limit, promo/discount, interest rate, and continued with weights of priorities are 0408, 0.28, 0.16, and 0.152.
Keywords: AHP, Fuzzy Analytic Hierarchy Process (FAHP), Criteria of Credit Card, Consistensy Ratio , Weight Priority
Mengikuti perkembangan zaman saat ini, aspek finansial yang berkembang pesat dalam satu sisi kehidupan masyarakat adalah maraknya penggunaan kartu kredit. Kartu kredit merupakan alat pembayaran pengganti uang tunai dan dapat digunakan di tempat-tempat yang bersedia menerima pembayaran menggunakan kartu kredit yang dimiliki oleh orang tersebut (Suyatno, T., dkk. 1997).
Pada penelitian ini akan dipelajari prioritas kriteria nasabah dalam pembuatan kartu kredit di suatu bank. Metode yang digunakan untuk menentukan prioritas tersebut adalah Fuzzy Analytic Hierarchy Process (FAHP). Fuzzy Analytic Hierarchy Process (FAHP) merupakan salah satu metode yang dipakai untuk mendukung keputusan. Metode ini merupakan gabungan dari metode Analytic Hierarchy Process (AHP) dan pendekatan
fuzzy khususnya pendekatan triangular fuzzy number.
Logika fuzzy merupakan sebuah logika yang memiliki nilai kekaburan atau kesamaran (Fuzzyness) antara dua nilai. Pendekatan fuzzy khususnya pendekatan triangular fuzzy number terhadap skala AHP diharapkan mampu untuk meminimalisasi ketidakpastian sehingga diharapkan hasil yang diperoleh lebih akurat (Kusumadewi dan Purnomo, 2010).
Berdasarkan latar belakang masalah, maka yang menjadi rumusan permasalahan dalam penelitian ini adalah bagaimana membangun sistem pengambilan keputusan pemilihan kriteria dalam pembuatan kartu kredit dengan menggunakan metode Fuzzy Analitical Hierarchy Process (FAHP) sebagai alat bantu dalam mengambil keputusan untuk menentukan prioritas kriteria yang akan dipilih.
Tujuan dari penelitian ini adalah untuk membangun sistem pengambilan keputusan sebagai alat bantu dalam mengambil keputusan untuk menentukan urutan prioritas kriteria yang akan dipilih nasabah dalam pembuatan kartu kredit dan menerapakan metode FAHP dalam sistem pengambilan keputusan studi kasus pemilihan kriteria dalam pembuatan kartu kredit.
Dalam penelitian ini, untuk menghindari terlalu luasnya masalah, maka batasan kriteria-kriteria yang dipakai dalam pembuatan kartu kredit adalah suku bunga, promo/diskon, limit, dan iuran tahunan. Sistem pendukung keputusan yang dirancang yaitu menggunakan metode fuzzy AHP.
Penelitian ini diharapkan dapat memberikan manfaat sebagai bahan masukan atau informasi bagi bank penerbit kartu kredit tentang kriteria prioritas nasabah dalam pembuatan kartu kredit. Hasil penelitian ini juga bermanfaat sebagai acuan pengambilan keputusan dalam meningkatkan kuantitas nasabah pengguna kartu kredit.
AHP merupakan suatu metode pengambilan keputusan dan suatu teori pengukuran yang digunakan untuk mengukur skala rasio, baik dari
perbandingan-perbandingan berpasangan
diskrit maupun kontinu (Saaty, 1987 ).
Tahapan-tahapan proses dalam metode AHP (Apriyanto, 2008) adalah:
-
a) Mendefinisikan masalah dan tujuan yang diinginkan.
-
b) Membuat struktur hirarki yang diawali
dengan tujuan, kriteria-kriteria dan alternatif-alternatif pilihan.
-
c) Membentuk matriks perbandingan
berpasangan terhadap masing-masing kriteria untuk analisis numerik.Nilai numerik yang diberikan untuk seluruh perbandingan diperoleh dari skala 1
sampai 9 yang telah ditetapkan, seperti tampak pada Tabel 1.
Tabel 1. Skala Penilaian Perbandingan Berpasangan
|
Tingkat Kepentingan |
Definisi |
|
1 |
Sama penting |
|
3 |
Sedikit lebih penting |
|
5 |
Lebih penting |
|
7 |
Sangat penting |
|
9 |
Mutlak lebih penting |
|
2,4,6,8 |
Nilai diantara dua pilihan yang berdekatan |
|
Resiprokal |
Kebalikan |
Sumber: Saaty, T. L. and L. G. Vargas (2012)
-
d) Menguji konsistensi hirarki. Jika nilai konsistensi rasio yang dihasilkan tidak memenuhi standar yang ditetapkan yaitu Consistency Ratio (CR) < 0,1 maka
penilaian harus diulang kembali.
-
2.2 Eigen value dan Eigen vector
Jika matriksA berukuran n x n , dapat didiagonalkan dan λ1,λ2, ...,λn merupakan nilai eigen dari A yang memenuhi hubungan
∣λ1∣>∣λ2∣≥-∣λn∣>0
Karena matriksA dapat didiagonalkan, vektor eigenv1,... ,vn masing-masing
berkaitan dengan eigen λ1,λ2, ...,λn dan membentuk basis di Rn. sehingga sebarang vektor x0 di Rn dapat dituliskan sebagai (Budhi, 1995):
Xo = SiVi + S2V2 + ... + snvn(Γ)
Jika persamaan (1) dikalikan denganA, diperoleh
Ax0 = A(s1v1 + S2V2 + ... + snVn )
= S1Av1 + S2Av2 + ... + snAvn = s1λ1v1
+ S2λ2V2 + ...
+ SnλnVn
Dari hasil Ax0 untuk memperoleh AkX0 maka dilakukan perkalian dari hasil terakhir
dengan A, hal ini dilakukan berulang-ulang sampai dengan k kali.
AkX0 = S1AkV1 + S2A⅛V2 + ... + SnAnVn
kC^ ^2 ^H^
= a1(s1v1 + S2 (^) v2 + .+ sn(77) Vn)
(2)
Jika k makin besar, nilai
(⅛)k
akan makin
kecil untuk i = 2, . . . ,n, karena |y| < 1.
Oleh karena itu, untuk k yang cukup besar pada persamaan (2) kurang lebih akan menjadi
Akx0 ≈ s1λkv1 (3)
Persamaan (3) merupakan hampiran dari kelipatan vektor eigen V1 tersebut, yaitu vektor AkX0. Vektor AkX0 merupakan hampiran vektor eigen yang berkaitan dengan nilai eigen terbesar V1. Makin besar nilai k makin baik pula hampiran AkX0 terhadap sebuah vektor eigen dari A.
Setelah diperoleh vektor eigenV1 atau kelipatannya, nilai eigen yang berkaitan dapat dihitung sebagai berikut. Karena Av1 = A1v1, maka
Av1v1 = A,1v1v1
-
2. Menentukan nilai Consistency Index yang dapat diperoleh dengan persamaan:
pτ _ (Amax n) (n-V
dengan,
CI =Rasio penyimpangan (deviasi)
konsistensi (consistency index)
Amax= Nilai eigen terbesar dari matriks berordo n
N = Ordo matriks
Apabila CI bernilai nol, maka pair-wise comparison matrix tersebut konsisten. Batas ketidakkonsistenan (inconsistency) yang telah ditetapkan oleh Saaty (1987) ditentukan dengan menggunakan Rasio Konsistensi (CR), yaitu perbandingan indeks konsistensi (CI) dengan nilai random indeks (RI) yang diperlihatkan pada Tabel 2. Nilai ini bergantung pada ordo matriks n. Dengan demikian, Rasio Konsistensi dapat dirumuskan sebagai berikut:
CR=£
CR = Consistency Ratio RI = RandomIndex
atau
, _ TlV1V1
Al--——
1 V1V1
Rumus nilai eigen ini disebut rumus
Tabel 2. Nilai Random Indeks (RI)
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R |
0. |
0. |
0. |
0. |
1. |
1. |
1. |
1. |
1. |
1. |
|
I |
00 |
00 |
52 |
89 |
11 |
25 |
35 |
40 |
45 |
49 |
Sumber: Saaty, T. L. and L. G. Vargas (2012)
pembagian Rayleigh (Budhi, 1995).
Dengan metode AHP yang memakai persepsi pembuat keputusan sebagai inputnya maka ketidakkonsistenan mungkin terjadi karena manusia memiliki keterbatasan dalam menyatakan persepsinya. Berdasarkan kondisi ini, untuk menunjukkan matriks berordo n konsisten dapat diperoleh melalui langkah-langkah berikut ini (Saaty, T, L, and L, G. Vargas, 2012):
-
1. Menentukan nilai vektor eigen dan Amax
Bila matriks pair–wise comparison mempunyai nilai CR <0,100 maka ketidakkonsistenan pendapat dari pengambil keputusan masih dapat diterima dan apabila tidak demikian maka penilaian harus diulang.
Jika hasil memenuhi CR < 0,100 maka dilakukan pengubahan bobot penilaian perbandingan berpasangan pada skala AHP ke dalam bilangan triangular fuzzy (Chang, D.Y., 1992).
Tabel 3. Fungsi Keanggotaan Bilangan Fuzzy
|
Skala Fuzzy |
Invers Skala Fuzzy |
Definisi |
|
1 dengan nilai TF (1, 1, 1) |
(1, 1, 1) |
Sama penting |
|
2 dengan nilai TF (1/2, 1, 3/2) |
(2/3, 1, 2) |
Pertengahan |
|
3 dengan nilai TF (1, 3/2, 2) |
(1/2, 2/3, 1) |
Sedikit lebih penting |
|
4 dengan nilai TF (3/2, 2, 5/2) |
(2/5, 1/2, 2/3) |
Pertengahan |
|
5 dengan nilai TF (2, 5/2, 3) |
(1/3, 2/5, 1/2) |
Lebih penting |
|
6 dengan nilai TF (5/2, 3, 7/2) |
(2/7, 1/3, 2/5) |
Pertengahan |
|
7 dengan nilai TF (3, 7/2, 4) |
(1/4, 2/7, 1/3) |
Sangat penting |
|
8 dengan nilai TF (7/2, 4, 9/2) |
(2/9, 1/4, 2/7) |
Pertengahan |
|
9 dengan nilai TF (4, 9/2, 9/2) |
(2/9 2/9, 1/4) |
Mutlak lebih penting |
Sumber: Chang, D.Y. (1992)
Selanjutnya diberikan aturan-aturan operasi aritmatika triangular fuzzy number yang umum digunakan. Misalkan terdapat 2 TFN yaitu: M1= (l1,m1,u1) danM2 = (l2,m2,u2), berlaku
Mi Φ M2 =(lι+12, mi + m2, ui + U2)
Mi Θ M2 = (li-12, mi - m2, ui - U2)
Mi ® M2 =(li.l2, mi.m2, Ui.U2)
A® M2 =(λ.l2, λ .m2, λ .U2)
M11 = (1 / ui, 1 / mi, 1/ li)
Dari matriks triangular fuzzy ditentukan nilai fuzzy synthetic extent untuk setiap kriteria (Chang, D. Y. 1996).
m r n m r1
Si= φ M<®l Φ Φ mΛ∣ (4)
j = 1 Li = V = 1 J
Setelah itu membandingkan nilai fuzzy synthetic extent (Si≥Sk). Dari hasil perbandingan nilai fuzzy synthetic extent(Si≥Sk) maka diambil nilai minimumnya, yaitu: d’l= min V(Si≥Sk)
Menghitung normalitas vektor bobot dan nilai minimum dilakukan untuk memperoleh
nilai masing-masing kriteria sehingga diperoleh prioritas dari kriteria tersebut.
W= (d1, d2, …, dn)T
Dengan perumusan normalisasinya adalah:
dι = y^u untuk l = 1, 2, • • - n (5) ∑i=ι a'i
Pengolahan data pada penelitian ini menggunakan bantuan program Excel, untuk mencapai tujuan penelitian digunakan metode FAHP. Adapun langkah-langkah analisis data dalam penelitian ini adalah:
-
1. Menyusun kriteria meliputi: suku bunga, promo/diskon, limit, dan iuran.
-
2. Menyebarkan kuisioner kepada responden dengan skala AHP yang telah ditetapkan menurut Saaty, T, L (1987).
-
3. Menyusun bobot nilai kriteria dari hasil rataan kuisioner yang telah diisi pada matriks berpasangan.
-
4. Menguji konsistensi hirarki. Jika tidak memenuhi dengan CR < 0,100 maka
penilaian diulang dengan perbaikan perbandingan berpasangan.
-
5. Jika hasil memenuhi CR < 0,100 maka dilakukan pengubahan bobot penilaian perbandingan berpasangan pada skala AHP ke dalam bilangan triangular fuzzy.
-
6. Dari matriks triangular fuzzy ditentukan nilai fuzzy synthetic extent untuk tiap-tiap kriteria dan sub kriteria, dengan menggunakan persamaan (1).
-
7. Membandingkan nilai fuzzy synthetic extent (Si≥Sk) .
-
8. Dari hasil perbandingan nilai fuzzy synthetic extent maka diambil nilai minimumnya, yaitu: d’i = min V(Si≥Sk)
-
9. Menghitung normalitas vektor bobot dan nilai minimum dilakukan untuk memperoleh nilai masing-masing kriteria sehingga diperoleh prioritas dari kriteria tersebut dengan menggunakan persamaan (5).
4. Hasil dan Pembahasan
Berdasarkan identifikasi data yang telah dilakukan dari hasil wawancara kemudian disusun menjadi sebuah struktur hirarki yang merupakan tujuan dari pemecahan masalah pengambilan keputusan dalam penelitian ini yaitu pemilihan kriteria dalam pembuatan kartu kredit. Kriteria yang telah dipilih adalah suku bunga, promo/diskon, limit, dan iuran tahunan. Selengkapnya dapat di lihat pada Gambar 1 berikut ini
f. 5.07324 mendekati 5 yang artinya limit lebih penting dari pada iuran tahunan.
Dari perhitungan di atas diperoleh perbandingan berpasangan sebagai berikut:
Tabel 4. Matriks Perbandingan Berpasangan
A
B
C
D
A
1
1/3
1/3
2
B
3
1
1/3
3
C
3
3
1
5
D
1/2
1/3
1/5
1
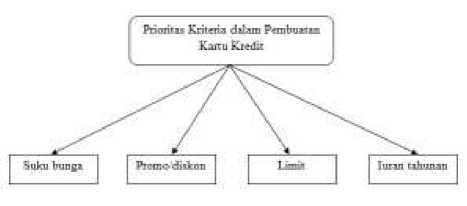
Gambar 1. Struktur Hirarki Kriteria
Selanjutnya untuk mendapatkan λmaksimum, langkah pertama adalah menghitung nilai vektor eigen yaitu: dengan cara mengalikan vektor perbandingan berpasangan untuk semua kriteria sampai mencapai nilai tertentu.
Pada langkah awal penelitian menyebar kuisioner kepada 50 responden yang mempunyai kartu kredit. Dari hasil kuisioner dibentuk matriks perbandingan antar kriteria. Dari sini setiap kriteria dicari nilai rata-ratanya. Selanjutnya nilai rata-rata dibulatkan ke nilai yang mendekati skala penilaian perbandingan berpasangan AHP yang terdapat pada Tabel 1.
yaitu
-
a. 0.33676 mendekati 1/3 yang merupakan kebalikan dari 3 yang artinya promo sedikit lebih penting dari pada suku bunga
-
b. 0.33656 mendekati 1/3 yang merupakan kebalikan dari 3 yang artinya limit sedikit lebih penting dari pada suku bunga
-
c. 2.24428 mendekati 2 yang artinya suku bunga diantara sama penting dan sedikit lebih penting dari pada iuran tahunan
-
d. 0.3293 mendekati 1/3 yang merupakan kebalikan dari 3 yang artinya limit sedikit lebih penting dari pada promo
-
e. 3.34028 mendekati 3 yang artinya promo sedikit lebih penting dari pada iuran tahunan
1
0.333
0.333
2
1 0.333
0.333
2
3
1
0.333
3
■
3
1
0.333
3
3
3
1
5
3
3
1
5
0.5 0.333
0.2
1
0.5 0.333
0.2
1
4
2.331
1.177
6.664
8.499
4
2.265
13.665
17.5
8.664
4
25
2.599
1.433
0.667
4
[
4
2.331
1.177
6.664
4
2.331
1.177
6.664
8.499
4
2.265
13.665
8.499
4
2.265
13.665
17.5
8.664
4
25
■ 17.5
8.664
4
25
2.599
1.433
0.667
4
2.599
1.433
0.667
4
]
=[
[
73.728
143.145
278.613
44.819
38.395
75.017
145.93
23.388
19.207
37.375
73.146
11.721
114.59
222.582
435.014
69.827
]
[
73.728
143.145
278.613
44.819
38.395
19.207
114.59
75.017
37.375
222.582
145.93
73.146
435.014
23.388
11.721
69.827
I ■
73.728
143.145
278.613
44.819
38.395
75.017
145.93
23.388
19.207
37.375
73.146
11.721
114.59
222.582
435.014
69.827
]
21418.999
41681.167
81307.048
13047.490
11193.973
21783.484
42492.880
6818.883
5599.131
10895.862
21254.590
3410.752
33351.317
64901.301
126602.912
20316.166
Setelah itu untuk mendapatkan nilai vektor eigen dari hasil perkalian terakhir vektor perbandingan berpasangan untuk semua kriteria yaitu dengan menjumlahkan setiap
-
nilai baris dan hasil penjumlahan tersebut dijumlahkan kembali kemudian setiap elemen dibagi dengan jumlah tersebut sehingga diperoleh nilai vektor eigennya.
Tabel 5. Vektor Eigen
|
A |
B |
C |
D |
∑ |
Vektor Eigen | |
|
A |
21418.99< |
11193.97' |
5599.131 |
33351.317 |
71563.421 |
0.136 |
|
B |
41681.167 |
21783.484 |
10895.862 |
64901.301 |
139261.81 |
0.265 |
|
C |
81307.048 |
42492.880 |
21254.590 |
126602.912 |
271657.43( |
0.516 |
|
D |
13047.49( |
6818.883 |
3410.752 |
20316.166 |
43593.290 |
0.083 |
|
∑ |
526075.89! |
Karena CR < 0,100 berarti preferensi
responden adalah konsisten, maka perbandingan berpasangan AHP diubah ke dalam perbandingan berpasangan fuzzy AHP yaitu sebagai berikut.
a) Membuat matriks perbandingan
berpasangan fuzzy yaitu dengan cara menggantikan nilai skala AHP dengan nilai skala bilangan segitiga fuzzy yang terdapat pada Tabel 6
Untuk mencari λmaksimum diperoleh dari mengalikan hasil perkalian terakhir vektor perbandingan berpasangan untuk semua kriteria dengan vektor eigen dan membagikan kembali terhadap vektor eigen Akv = λkv. Maka diperoleh nilai λmaksimum sebagai berikut:
Tabel 6. Matriks Perbandingan Berpasangan Fuzzy AHP
'21418.999 11193.973 5599.131 33351.317'
41681.167 21783.484 10895.862 64901.301
81307.048 42492.880 21254.590 126602.912
13047.490 6818.883 3410.752 20316.166
|
A |
B |
C |
D | |||||||||
|
l |
m |
u |
l |
m |
u |
l |
m |
u |
l |
m |
u | |
|
A |
1 |
1 |
1 |
1/2 |
2/3 |
1 |
1/2 |
2/3 |
1 |
1/2 |
1 |
3/2 |
|
B |
1 |
3/2 |
2 |
1 |
1 |
1 |
1/2 |
2/3 |
1 |
1 |
3/2 |
2 |
|
C |
1 |
3/2 |
2 |
1 |
1.5 |
2 |
1 |
1 |
1 |
2 |
5/2 |
3 |
|
D |
2/3 |
1 |
2 |
1/2 |
2/3 |
1 |
1/3 |
2/5 |
1/2 |
1 |
1 |
1 |
Menghitung nilai fuzzy synthetic extent.
r 0.136] r11531.888] 0.265 = 22440.975
0.516 43775.524
0.083 7024.722
b)
Si =
I
11531.888/0.136
22440.975/0.265
43775.524/0.516
7024.722/ 0.083
M84773.045] 84773.113 84773.131 84773.080
m r
.φ ,∙⅛β∣ y = 1 Li
n
Φ
m
= 1Λ*⅛
I-1
Jadi, λmaksimum = √84773.131
= 4.131
Karena matriks berordo 4 (yakni terdiri dari 4 kriteria), nilai indeks konsistensi yang diperoleh:
CJ _ λmax-n _ 4.131-4
Ti-I 4-1
0.131
3
= 0.044
Untuk extent
menghitung nilai fuzzy synthetic
yang
pertama
menghitung
(m
/ = 1'" operasi bilangan baris.
m
∑
i = 1
nilai
m',
adalah dengan m
Φ Mi- =
7 = 1 '
m \ 7=1“')
dengan
penjumlahan pada tiap-tiap triangular fuzzy dalam setiap
Tabel 7. Nilai Fuzzy Synthetic Exten
|
lA,B,C,D |
mA,B,C,D |
uA,B,C,D |
|
5/2 |
10/3 |
9/2 |
|
7/2 |
28/6 |
6 |
|
5 |
13/2 |
8 |
|
15/6 |
46/15 |
9/2 |
Berdasarkan Tabel 2 Untuk n = 4, maka RI = 0.89, maka:
CR = = 01044= 0.049
R/ 0.89
Kemudian menghitung
" " ..,1.
nilai Φ φ M1i dengan operasi
L ι = ii = ι flJ
c) Menghitung perbandingan tingkat kemungkinan antar fuzzy syntethic extent dengan nilai minimumnya.
penjumlahan untuk keseluruhan bilangan triangular fuzzy dalam matriks perbandingan berpasangan.
Langkah pertama adalah memperbandingkan nilai setiap fuzzy syntethic extent V(S2 ≥ S1),yaitu:
Tabel 8. Jumlah Fuzzy Synthetic Extent
|
lA,B,C,D |
mA,B,C,D |
uA,B,C,D | |
|
A |
2.5 |
3.333 |
4.5 |
|
B |
3.5 |
4.667 |
6 |
|
C |
5 |
6.5 |
8 |
|
D |
2.5 |
3.067 |
4.5 |
|
∑ |
13.5 |
17.567 |
23 |
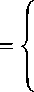
V(S1≥S2)
V(S1≥S3)
I, jlkam2 ≥ m1
O, jlkal1 ≥ u2
11 — ^2
-------;—;----— lainnya (m2 - U2) - (m1 - l1)
0.152-0.333
(0.189-0.333)-(0.266-0.152)
0.217-0.333
(0.189-0.333)-(0.369-0.217)
= 0.702
= 0.392
r n m j-1
Jadi untuk nilai I Φ Φ M1ai I adalah
L I = H = I flJ
V(S1≥S4) = 1
V(S2≥S1) = 1
(23’17.567’13.5/
selanjutnya dihitung nilai fuzzy syntethic extent untuk tiap kriteria utama dengan.
S1 = (2.5, 3.334, 4.5) Φ (⅛q⅛,⅛)
Zd 1 /. d o / 1d. d/
= (0.109, 0.189, 0.333)
S2 = (3.5, 4.667, 6) 8(⅛,⅛⅛) Zd 1/.do/ 1d.d/
= (0.152, 0.266, 0.444)
S3 = (5, 6.5, 8) Φ⅛τ⅛7,⅛) Zd 1/.do/ 1d.d/
= (0.217, 0.369, 0.593)
S4 = (2.5, 3.067, 4.5) Θ⅛1⅛⅛)
Zd 1/.do/ 1d.d/
= (0.109, 0.175, 0.333)
Jadi nilai fuzzy syntethic extent untuk tiap
kriteria dapat dilihat pada Tabel 9
Tabel 9. Nilai fuzzy syntethic extent untuk tiap kriteria utama
|
l |
m |
u | |
|
S1 |
0.109 |
0.189 |
0.333 |
|
S2 |
0.152 |
0.266 |
0.444 |
|
S3 |
0.217 |
0.369 |
0.593 |
|
S4 |
0.109 |
0.175 |
0.333 |
V(S2≥S3)
0.217-0.444
(0.266-0.444)-(0.369-0.217)
= 0.688
|
V(S3≥S4) |
= 1 |
|
∖7fQ.>Q1^ |
0.109-0.333 = = 0.941 |
|
(0.175-0.333)-(0.189-0.109) | |
|
∖77Q.>Q^ |
0.152-0.333 |
|
(0.175-0.333)-(0.216-0.152) | |
|
∖77Q.>Q^ |
_ 0.217-0.333 = = 0.374 |
|
(0.175-0.333)-(0.369-0.217) |
Setelah didapat nilai perbandingan dari setiap fuzzy syntethic extent lalu diambil nilai minimumnya, yaitu:
d’i = min V(Si≥Sk) untuk k = 1, 2, …, n; k ≠i.
d’1 = V(S1≥S2, S3, S4)
= min(0.702, 0.392, 1)
= 0.392
d’2 = V(S2≥S1, S3, S4)
= min(1, 0.688, 1)
= 0.688
d’3 = V(S3≥S1, S2, S4)
= min(1, 1, 1)
= 1
d’4 = V(S4≥S1, S2, S3)
= min(0.941, 0.665, 0.374)
= 0.374
Kemudian dilakukan perhitungan bobot dan normalisasi vektor bobot sehingga diketahui nilai bobot kriteria utama.
W’= (d’1, d’2, d’3, d’4)T
W’ = (0.392, 0.688, 1, 0.374)
danW= (di, d2, d3, d4)τdengan dl = ^;-∑i=ι “‘
menghasilkan normalisasi vektor bobot antar kriteria utamanya yaitu:
W= (0.16, 0.28, 0.408, 0.152)
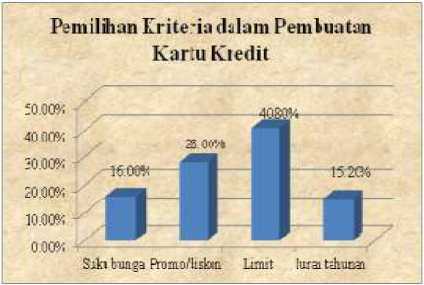
Dari uji konsistensi dapat dilihat bahwa bobot prioritas pada kriteria utama yaitu limit (d3), promo/diskon (d2), suku bunga (d1), dan iuran (d4), adalah 0.408, 0.28, 0.16, dan 0.152.
Gambar 2. Bobot Prioritas Pemilihan Kriteria dalam Pembuatan Kartu Kredit
5. Kesimpulan
Berdasarkan hasil yang telah diperoleh pada kasus Pemilihan Kriteria dalam Pembuatan Kartu Kredit, maka dapat ditarik kesimpulan bahwa metode Fuzzy AHP dapat digunakan untuk menentukan bobot prioritas pada masing-masing kriteria. Dari hasil analisis bobot prioritas pada kriteria utama dengan Fuzzy AHP, kriteria limit mempunyai pengaruh paling besar bagi nasabah dalam menggunakan kartu kredit sebesar 40.8%, sedangkan promo/diskon sebesar 28%, suku bunga sebesar 16% dan yang terakhir adalah iuran tahunan sebesar 15,2%. Dari melihat hasil total rangking di atas, disarankan kepada bank-bank agar dapat melihat peluang yang lebih baik untuk memberikan penawaran-
penawaran dalam menarik nasabah untuk membuat kartu kredit
Daftar Pustaka
Apriyanto, Agus, 2008, Perbandingan
Kelayakan Jalan Beton dan Aspal dengan Metode Analityc Hierarchy Process (AHP) (Studi Kasus Jalan Raya Demak-Godong), Thesis tidak diterbitkan, Semarang, Program Pascasarjana Universitas Diponegoro
Budhi, Wono Setya, 1995. Aljabar Linier. Jakarta:Gramedia Pustaka Utam
Chang, D.Y., 1992, Extent Analysis and Synthetic Decision, Optimization Techniques and Applications, World Scientific, Singapore, 1:352
___________. 1996. Applications of The Extent Analysis Method on Fuzzy AHP. European Jurnal of Operational Research, 95, 649-655.
Kusumadewi, Sri dan Hari Purnomo, 2010, Aplikasi Logika Fuzzy Untuk Pendukung Keputusan, Edisi 2, Graha Ilmu, Yogyakarta
Saaty, T, L, 1987, Uncertainty and Rank Order in The Analytic Hierarchy Process.
European Journal of Operation Research 32:27-37
Saaty, T, L, and L, G. Vargas, 2012. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process, International Series in Operations Research & Management Science, Vol. 175, 2 nd edition. New York: Springer
Suyatno, T., dkk. 1997. Dasar-dasar Perkreditan. Jakarta : PT. Gramedia Pustaka Utama.
32
Discussion and feedback