PENGKLASIFIKASIAN STATUS GIZI BALITA MENGGUNAKAN ANALISIS DISKRIMINAN
on
E-Jurnal Matematika Vol. 12(1), Januari 2023, pp. 22-30
DOI: https://doi.org/10.24843/MTK.2023.v12.i01.p395
ISSN: 2303-1751
PENGKLASIFIKASIAN STATUS GIZI BALITA MENGGUNAKAN ANALISIS DISKRIMINAN
Diana1§, Made Susilawati2, I Komang Gde Sukarsa3, I Putu Eka Nila Kencana4
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana[Email: diazkadiana@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac,id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: gedesukarsa@unud.ac.id]
-
4Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: i.putu.enk@unud.ac.id]
§Corresponding Author
ABSTRACT
Nutrition is one of the risks that trigger morbidity and mortality. Malnutrition, especially at an early age, will increase infant and child mortality and have short stature as adults. The standard that can be used to measure chronic nutritional status is to classify the nutritional status of toddlers based on height according to age, one of the methods that can be used in this classification is discriminant analysis. Discriminant analysis is a statistical analysis used to classify individual status into classes or groups based on a set of variables. The classification of the nutritional status of children under five is categorized into stunting and normal groups based on the variables under five, birth length, birth weight, anemia status and mother's age during pregnancy using discriminant analysis on secondary data taken in 2015 as many as 116 samples, with birth weight X3 as an indicator of participation in model with a classification accuracy rate of 65.6% on training data and 74% on testing data.
Keywords: Classification, Nutritional Status, Stunting, birth weight, Discriminant Analysis.
Menurut kementrian kesehatan Indonesia (2017) status gizi merupakan salah satu faktor risiko yang memicu terjadinya kesakitan dan kematian. Status gizi yang baik akan berkontribusi yang baik pula bagi kesehatan seseorang. Sedangkan kekurangan gizi terutama pada usia dini akan meningkatkan angka kematian bayi dan anak, menyebabkan penderitanya mudah sakit, serta kecenderungan kurang gairah dan lincah serta memiliki postur tubuh tak maksimal saat dewasa (Millennium Challenge Account- Indonesia).
Untuk menilai status gizi anak balita dapat diukur berdasarkan standar antropometri penilaian status gizi anak yang terdiri dari 3 indikator dan telah dikonversikan ke dalam nilai terstandar (Zscore) yaitu berat badan menurut umur (BB/U) digunakan untuk menilai
kemungkinan gizi kurang atau buruk, tinggi badan menurut umur (TB/U) digunakan untuk menggambarkan keadaan kurang gizi kronis yaitu Stunting dan berat badan dengan tinggi badan (BB/TB) untuk menilai kemungkinan status gizi kurus dan sangat kurus. Salah satu cara yang dapat dilakukan untuk menilai status gizi dengan cara mengelompokan atau mengklasifikasikan keadaan gizi.
Klasifikasi merupakan metode pengelompokan yang mengelompokan sekumpulan objek kedalam kelompok-kelompok yang lebih kecil dimana anggota dari masing-masing kategori kelompok yang dibentuk tersebut mempunyai kesamaan ciri yang sesuai dengan kategori kelompoknya. Berbagai metode analisis dapat digunakan dalam proses pengklasifikasian, beberapa diantaranya yaitu regresi logistik, multivariate adaptive regression spline dan Analisis
Diskriminan. Dari beberapa metode tersebut yang dapat digunakan dalam pemisahan kelompok menjadi sekumpulan kelompok yang baru yaitu Analisis Diskriminan.
Analisis Diskriminan merupakan analisis multivariate yang termasuk teknik dependensi (hubungan antar variabel yang sudah dapat dibedakan antar variabel respon dengan variabel bebas) dengan variabel respon yang bersifat kategori (berskala nominal atau ordinal dan kualitatif) dan variabel independen yang bersifat metrik (berskala interval atau rasio dan kuantitatif). Analisis diskriminan adalah teknik statistika yang digunakan untuk
mengklasifikasikan suatu individu atau observasi kedalam suatu kelas atau kelompok berdasarkan sekumpulan variabel-variabel (Johnson dan Winchern, 2007). Sebelum melakukan Analisis Diskriminan, ada beberapa asumsi yang harus dipenuhi yaitu (1) variabel independen bersifat multivariate normal, (2)
hubungan antar variabel dependen dan independen bersifat linier; (3) tidak ada korelasi antar variabel independen dan (4) kehomogenan matriks varian kovarian antar kelompok (Hair Jr et al, 2010).
Mencermati beberapa hal yangtelah dipaparkan, penelitian ini dilakukan dengan mengaplikasikan analisis diskriminan untuk mengklasifikasikan status gizi balita berdasarkan indikator tinggi badan menurut umur (TB/U) yang dikategorikan berdasarkan kejadian Stunting dan Normal dengan variabel bebas yaitu umur balita, panjang badan lahir, berat badan lahir, status anemia ibu, dan umur ibu saat hamil dengan tujuan, yaitu:
-
1 Untuk Mengetahui faktor yang berpengaruh pada pengelompokan status gizi balita yaitu kejadian Stunting dan normal.
-
2 Mengetahui bagaimana tingkat ketepatan klasifikasi pada kejadian Stunting dan normal pada balita menggunakan analisis diskriminan.
Fungsi Diskriminan merupakan fungsi pembeda (pemisah) yang diperoleh dari kombinasi linier digunakan untuk mementukan suatu objek masuk kedalam kelompok yang mana. Adapun Fungsi Diskriminan dapat dituliskan sebagai berikut (Hair Jr et al., 2010):
^jk — d + Wi^ik + ^2^2k + ■" +wnxnk
— a+ ∑ι=ιwixik
(1)
Nilai Diskriminan Z pada persamaan (1) merupakan dasar dalam menentukan suatu objek masuk kedalam kelopok yang mana dengan membandingkannya dengan rata-rata (centroid) dari nilai Diskriminan Z masing- masing kelompok. Misalkan ada dua kelompok A dan B, maka:
Z = z, CU
Dimana:
naZb+nbZa na+nb
(2)
Zcu:nilai Z cut off (cutting score)
NA: jumlah objek didalam A
NB: jumlah objek didalam B
Za: centroid untuk A; Zb: centroid untuk B
Masukkan objek kedalam kelompok A jika Zn<Zcu dan kelompokkan objek kedalam kelompok B jika Zn>Zcu dimana Zn merupakan nilai Z untuk masing-masing kelompok (Hair Jr et al., 2010).
Pada analisis diskriminan ada beberapa asumsi yang harus dipenuhi sebelum membangun model yaitu :
Proses uji distribusi normal (Univariate) dilakukan dengan salah satu pendekatan yang sering digunakan yaitu plot pasangan nilai jarak Mahalanobis terhadap [d2],x2 θ-^). Nilai dari jarak Mahalanobis dapat diperoleh menggunakan persamaan sebagai berikut:
d2 — (xi — xyS-1(xi — X);
i —1,2.....n (3)
Keterangan:
xi = sampel pengamatan
X = vektor rata-rata
S-1= invers matriks ragam
Uji distribusi normal (Univariate) dilakukan pada variabel-variabel independent menggunakan plot jarak Mahalanobis terhadap khi-kuadrat dengan hipotesis sebagai berikut:
H0 = Data berdistribusi normal
H1 = Data tidak berdistribusi Normal
Menurut Johnson dan Winchern (2007) jika lebih dari 50% nilai dari dj < χ0.05γp, maka terima H0.
Proses pengujian nilai rataan terhadap vektor antar kelompok dapat dilakukan dengan hipotesis sebagai berikut:
H0 = μ0 = μ1 = μ2 = ••• = Mk
Hi = tedapat dua kelompok yang berbeda ( μi ≠ μ) i = 1,2, ... , k
Statistik uji yang digunakan pada proses pengujian hipotesis tersebut yaitu statistik uji V - Barlett yang merupakan stastistik uji yang mengikuti sebaran khi-kuadrat (∕2) dengan derajat bebas p(k - 1). Adapun statistik uji V -Barlett dapat diperoleh melalui:
V = [(n - 1) - (p + k)∕2] ln(∆)(4)
Sedangkan ∆ merupakan Wilk's lambda
Hasil pengujian hipotesis dapat dilihat apabila nilai V > Xp(k-1)(1-α) maka H0 ditolak yang menyatakan bahwa terdapat variabel yang memiliki perbedaan.
Menurut Morison dalam Maulidya dkk (2014), proses pengujian kehomogenan matrik varian- kowvarians (∑) dapat dilakukan dengan menggunakan statistik uji Box’s M, yang dirumuskan sebagai berikut:
-2lnλ* = (n - k)ln∖W∕(n - k)∖ -
∑f=1(nj - 1)ln∖Si∖ (6)
Dengan hipotesis sebagai berikut:
Ho^∑ι= ∑2 = - = ∑k= ∑(matriks varians-kovarians antar kelompok sama) H1: minimal terdapat satu koefisien
-
∑i≠∑ i = 1,2.....k
Apabila (-2lnλ*)∕b ≤ Fviιv2,α, maka
hipotesis nol (H0) diterima yang menyatakan antar kelompok mempunyai matrik varian-kowvarians yang sama sedangkan jika
(-2lnλ*}∕b > Fvι,v2,α maka hipotesis nol (H0) ditolak yang menyatakan antar kelompok tidak memiliki matriks varian-kovarians yang sama.
Mengambil taraf signifikansi a sebesar 0,05 , hipotesis nol (H0) akan ditolak apabila nilai statistik uji Box's M< a yang menyatakan bahwa matriks varian-kowvarians antar kelompok tidak homogen.
Proses pembentukan fungsi diskriminan, ada dua pendekatan yang dapat digunakan yaitu metode simultan dan estimasi stepwise. Metode simultan merupakan estimasi koefisien fungsi diskriminan yang memasukkan seluruh variable bebas secara serentak dan bersama-sama.
Johnson dan Winchern (2007) menyatakan bahwa prosedur klasifikasi merupakan evaluasi klasifikasi untuk mengetahui seberapa besar kesalahan oleh suatu fungsi klasifikasi dalam pengklasifkasian. Prosedur klasifikasi yang baik merupakann prosedur klasifikasi yang dapat mengevaluasi tingkat kesalahan klasifikasi dan menghasilkan tingkat kesalahan klasifikasi yang kecil. Apparent error rate (APPER) merupakan perhitungan yang digunakan untuk mengevaluasi tingkat kesalahan klasifikasi berdasarkan representasi proporsi sampel yang salah diklasifikasikan.
|
Keanggotaan sebenarnya |
Keanggotaan prediksi | |
|
π0 |
π1 | |
|
π0 |
π00 |
π01 = π0 - π00 |
|
π1 |
π10 = π1 -π11 |
π11 |
APER = ---n°1+nι°---χ ioo (7)
∏00+n01+n10+n11
Uji statistik Press’Q digunakan untuk mengetahui kestabilan dalam klasifikasi serta untuk melihat sejauh mana kelompok-
kelompok dapat dipisahkan. Uji statistik Press’Q dirumuskan sebagai berikut (Johnson dan Winchern, 2007):
Press'Q = [N~(nKy]2 (8)
N(K-1) v 7
Data yang digunakan dalam penelitian ini adalah data sekunder. Data sekunder merupakan data penelitian yang diperoleh secara tidak langsung melalui media perantara, dicatat dan diperoleh oleh pihak lain (Sugiono, 2014). Pada penelitian ini data sekunder berasal dari penelitian Suciari (2015) sebanyak 116 dengan objek penelitian adalah balita berumur 24-59 bulan di wilayah kerja UPT. Puskesmas Klungkung I.
Variabel respon (Y) yang digunakan dalam penelitian ini dikelompokkan berdasarkan indikator tinggi badan menurut umur yang dibedakan menjadi dua kategori yaitu kategori Stunting dan Normal. Penelitian ini menggunakan lima variabel prediktor berskala kontinue yaitu umur balita (%1), panjang badan lahir (x2), berat badan lahir (%3), Status anemia ibu (x4), dan Umur Ibu (x5).
Metode penelitian untuk mencapai tujuan penelitian diuraikan sebagai berikut:
-
1. Membagi data menjadi dua bagian yaitu 20% data Testing yang digunakan untuk menguji kelayakan fungsi dan 80% data Training yang digunakan untuk membentuk fungsi diskriminan.
-
2. Melakukan uji asumsi dasar analisis diskriminan, yaitu:
-
i. Melakukan uji distribusi normal ganda tehadap masing-masing variabel independen menggunakan plot jarak Mahalanobis terhadap khi-kuadrat
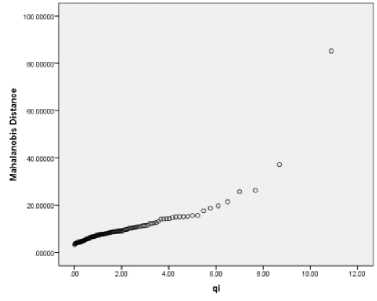
Gambar 1. Uji Distribusi Normal
-
ii. Melakukan uji kehomogenan
matriks varians-kovarians
menggunakan statistik uji Box’s M iii. Melakukan uji vektor nilai rataan menggunakan uji V — Barlett sesuai dengan Equality's Test of Group Means.
-
3. Melakukan estimasi fungsi
diskriminan menggunakan estimasi Stepwise.
-
4. Menetapkan dan mendapatkan model
terbaik berdasarkan estimasi Stepwise.
-
5. Melakukan uji ketepatan klasifikasi
yang terdiri dari:
-
i. Uji tingkat ketepatan
klasifikasi menggunakan
Apparent Error Rate (APER)
-
ii. Uji kestabilan klasifikasi menggunakan nilai Press’s Q
-
6. Interpretasi hasil
Penelitian ini data sekunder berasal dari penelitian Suciari (2015) sebanyak 116 dengan objek penelitian adalah balita berumur 24-59 bulan pada tahun 2015 di wilayah kerja UPT. Puskesmas Klungkung I. Kemudian dilakukan pembagian data menjadi dua yaitu 80% data yang digunakan untuk memebentuk fungsi yaitu sebanyak 93 sampel dan 20% data digunakan untuk menguji kelayakan fungsi diskriminan yaitu sebanyak 23 sampel.
Uji distribusi normal (Univariate) dilakukan terhadap variabel-variabel independent (bebas) menggunakan plot jarak Mahalanobis terhadap khi-kuadrat yang dapat dilihat pada gambar 1 dengan hipotesis sebagai berikut:
H0= Data berdistribusi normal
H1= Data tidak berdistribusi Normal
Menurut Johnson dan Winchern (2007) menyatakan bahwa jika lebih dari 50% nilai jarak mahalanobis (dj < X0.05:p) maka terima H0 begitu pula sebaliknya. Pada gambar 1 dapat dilihat bahwa scatter-plot cenderung membentuk garis lurus (mengkuti garis kenormalan). Kemudian jumlah data dengan nilai jarak mahalanobis untuk data ke-i yang kurang dari nilai Chi-square (∕2.05.5) = 11.07048 sebanyak 90 data dari 93 data yaitu hanya 3,2% nilai jarak mahalanobis yang lebih besar dari α =0,05 dan 96,8% data lebih kecil dari α =0,05, sehingga dapat disimpulkan bahwa terima H0, dan dapat dinyatakan bahwa data berdistribusi normal.
Pada proses pengujian kehomogenan matriks varian-kowvarians dilakukan dengan menggunakan statistik uji Boxs’M dengan hipotesis sebagai berikut:
H0: ∑ι = ∑2 = ∙∙∙ = ∑fc = ∑ (matriks varian-kowvarians antarkelompok sama)
H1: ∑ι≠∑ i = 1,2, ---,k (minimal terdapat satu kelompok yang berbeda dibanding kelompok lainnya).
|
Box’s M |
0,141 | |
|
F |
Approx. |
0,139 |
|
df1 |
1 | |
|
df2 |
17197,839 | |
|
Sig. |
0,709 | |
Nilai signifikansi (sig,) < α dengan a = 0.05 maka tolak H0 yang berarti bahwa matriks varian-kowvarians tidak homogen. Sedangkan pada Tabel 2 dapat dilihat bahwa nilai signifikansi dari uji Boks’M sebesar 0,141 maka sig (0,141) > a = 0,05 yang berarti bahwa terima H0, yang dapat dinyatakan bahwa matriks varian-kowvarians antar kelompok homogen.
Pengujian Vektor nilai rataan dilakukan untuk mengetahui ada atau tidaknya perbedaan antar kelompok. Proses pengujian terhadap vektor nilai rataan antar kelompok dapat dilakukan dengan hipotesis sebagai berikut:
H0 = μ0 = k1=k2 = ••• = kk
H1 =minimal tedapat dua kelompok yang berbeda ( μi ≠ μ) i = 1,2,... ,k
Tabel 3. Hasil Uji Vektor Nilai Rataan
|
Test of Equality of Group Means | |||||
|
Wilks’lambda |
F |
df1 |
df2 |
Sig. | |
|
Xi |
0,998 |
0,213 |
1 |
91 |
0,646 |
|
^2 |
0,997 |
0,308 |
1 |
91 |
0,580 |
|
X3 |
0,827 |
19,086 |
1 |
91 |
0,000 |
|
X4 |
1,000 |
0,019 |
1 |
91 |
0,890 |
|
x^ |
1,000 |
0,010 |
1 |
91 |
0,921 |
Statistik uji dengan nilai α = 0,05 dengan nilai p < a maka tolak H0 yang berarti bahwa terdapat perbedaan yang signifikan antar kelompok dan sebaliknya. Pada Table 3 terlihat bahwa X3 memeiliki p — value < a atau nilai signifikansi yang lebih kecil dari α = 0,05 yang berarti bahwa tolak H0 yang menyatakan bahwa
X3 atau berat badan lahir memeberikan perbedaan rataan pada pengelompokan status gizi balita. Sedangkan ke-empat variabel lainnya memiliki p — value > a yang dapat disimpulkan bahwa terima H0 yang menyatakan bahwa ke-empat variabel tersebut tidak memberikan perbedaan nilai rataan pada pengelompokan atau pengklasifikasian status gizi balita.
Pembentukan fungsi Diskriminan dilakukan dengan menggunakan pendekatan atau metode stepwise. Pendekatan stepwise pada kasus pengelompokan status gizi balita dilakukan dengan memasukkan variabel independen yang mempunyai pengaruh signifikan kedalam model. Proses tersebut dilakukan bertahap sampai didapatkan model terbaik. Tahapan memasukkan variabel independen kedalam model dimulai dengan memasukkan variabel independen yang memiliki nilai signifikan paling kecil, berikut tahapannya:
A.Tahap awal pada proses stepwise
Tabel 4. Hasil Uji Stepwise Tahap 0 untuk Data Training
|
Step |
Sig. of F to Enter |
Min.D Square |
Antar Kelompok | |
|
0 |
X1 |
0,646 |
0,010 |
1 dan 2 |
|
X? |
0,580 |
0,015 |
1 dan 2 | |
|
X3 |
0,000 |
0,939 |
1 dan 2 | |
|
X4 |
0,890 |
0,001 |
1 dan 2 | |
|
X5 |
0,921 |
0,000 |
1 dan 2 | |
Tabel di atas merupakan tahap awal dari proses pendekatan stepwise pada data Training yang menunjukkan bahwa variabel X3 yaitu berat badan lahir memiliki nilai Min. D Square sebesar 0,939 dan nilai signifikan F paling kecil yaitu 0,000 nilai sig. F (0,000) lebih kecil dari taraf signifikan α = 0,05 (sig. F = 0,015 < α) maka variabel X3 dapat digunakan dalam pembentukan fungsi diskriminan.
-
B.T ahap 1 pada proses stepwise .
Tabel 5. Hasil Uji Stepwise Tahap 1 untuk Data Training
|
Step |
Sig. of F to Enter |
Min D Squared |
Antar Kelompok | |
|
1 |
Xl |
0,591 |
0,957 |
1 dan 2 |
|
X? |
0,308 |
1,003 |
1 dan 2 | |
|
X4 |
0,897 |
0,940 |
1 dan 2 | |
|
X5 |
0,449 |
0,974 |
1 dan 2 | |
Pada Tabel 5 terlihat bahwa nilai sig. F X2 pada data Training sebesar 0.329. nilai sig. F sebesar 0.308 > α dengan α = 0.05 yang
menyatakan bahwa variable X2 tidak dapat digunakan dalam pembentukan fungsi Diskriminan karena keputusan diterima H0. Begitu pula dengan variabel-variabel lainnya yang memeiliki nilai Sig. F lebih besar dari taraf signifikan sebesar α = 0.05. Oleh karena itu dapat disimpulkan bahwa hanya satu variabel yang dapat diikutsertakan dalam pembentukan fungsi Diskrimanan yaitu variabel BBL (X3) sebagai variabel yang mendominasi pembentukan fungsi diskriminan pada pengujian data Training.
Tabel 6. Keeratan Hubungan Nilai Diskriminan dengan Kelompok untuk Data Training
|
Eigenvalues | ||||
|
Functi on |
Eigenvalue |
% of Variance |
Cumul ative % |
Canonical Correlation |
|
1 |
0,210a |
100,0 |
100,0 |
0,416 |
Pengukuran keeratan hubungan nilai diskriminan dengan kelompok dilihat berdasarkan nilai korelasi kanonik. Pada Tabel 6 yaitu nilai korelasi kanonik sebesar 0.416 untuk data Training yang menyatakan bahwa variabel Berat Badan Lahir dapat mendiskriminasi kelompok stunting dan normal pada Balita dipuskesmas 1 Klungkung yaitu sebesar 41%.
Tabel 7. Koefisien Pembentuk Fungsi untuk Data Training
|
Canonical Discriminant Function Coefficients | |
|
Function | |
|
1 | |
|
X3 |
0,003 |
|
(Constant) |
-7,746 |
Berdasarkan Tabel 7 diperoleh fungsi diskriminan untuk data Training sebagai berikut:
Ket:
X3: Berat Badan Lahir
Fungsi Z yang telah diperoleh digunakan untuk mengetahui sebuah sampel yakni balita di Puskesmas 1 Klungkung masuk kedalam kelompok stunting atau normal. Berat Badan Lahir (X3) merupakan faktor penentu seorang balita dapat dikelompokkan menjadi kelompok Stunting dan normal, dimana setiap penambahan berat badan lahir sebesar 1 gram mengakibatkan penurunan kemungkinan bayi masuk dalam kategori stunting dan dapat dikategorikan sebagai kelompok normal. Bayi dengan berat badan lahir normal akan mengalami pertumbuhan yang normal sesuai dengan usianya, sedangkan bayi dengan berat badan lahir rendah akan mengalami pertumbuhan yang lebih lambat dibanding bayi dengan berat badan lahir normal.
Tabel 8. Angka Centroid pada Masing-Masing Kelompok untuk Data Training
|
Functions at Group Centroids | |
|
Status |
function |
|
1 | |
|
Stunting |
-0,656 |
|
Normal |
0,313 |
Pada Tabel 8 dapat dilihat bahwa angka Centroid pada data Training yang didapat dari fungsi diskriminan yang terbentuk menunjukkan perbedaan dari dua kategori yang ada, angka Centroid ini akan digunakan untuk menentukan nilai Cutting Score sebagai perbadingan dengan nilai diskriminan untuk menentukan sampel atau balita di Puskesmas 1 Klungkung termasuk dalam kategori Stunting atau Normal dengan nilai Zcu adalah sebesar -0.343. nilai Zcu= -0,343 digunakan sebagai nilai batas untuk menentukan sampel masuk dalam kategori Stunting apabila nilai diskriminannya lebih kecil dari nilai batas Zcu= -0,343, dan masuk dalam kategori normal apabila nilai diskriminan dari sebuah sampel lebih besar dari nilai batas.
Hasil pengelompokan untuk data Training dapat dilihat pada Tabel dibawah ini:
Tabel 9. Hasil Klasifikasi Balita Sesuai dengan Fungsi Diskriminan untuk Data Training
|
Status |
Predicted Group Membership |
Total | |||
|
Stunting |
Normal | ||||
|
Origi nal |
Count |
Stunting |
22 |
8 |
30 |
|
Normal |
24 |
39 |
63 | ||
|
% |
Stunting |
73.3 |
27.6 |
100.0 | |
|
Normal |
38.1 |
61.9 |
100.0 | ||
Pada Tabel 9 dapat dilihat bahwa balita yang tepat diklasifikasikan sebagai kelompok normal pada data Training sebanyak 39 orang, sedangkan yang salah diklasifikasikan sebagai kelompok stunting yaitu 24 orang. Kemudian balita yang tepat diklasifikasikan sebagai kelompok stunting yaitu 22 orang, sedangkan yang salah diklasifikasikan sebagai kelompok normal yaitu 8 orang.
Evaluasi kesalahan dalam Pengklasifikasian untuk data Training akan diukur menggunakan APPER sebagai berikut:
(8 + 24\
APPER = (—) × 100% = 34,4%
Nilai APPER yang diperoleh untuk data Training menyatakan bahwa fungsi Diskriminan yang terbentuk memiliki tingkat kesalahan klasifikasi sebesat sebesar 34,4% yang berarti bahwa tingkat ketepatan klasifikasi sebesar 65,6%.
Kemudian dilakukan pengujian kestabilan klasifikasi untuk data Training menggunakan nilai Press’s Q
Press'Q
[23 - (17 x 2)]2 23(2-1)
5,26
Press'Q
[93- (61 x 2)]2 93(2 - 1)
9,68
Dapat dilihat bahwa nilai Press’Q sebesar 9,68 yang kemudian dibandingkan dengan nilai dari tabel χ2 yaitu χ2ιjo,o5) = 3,84 yang menyatakan bahwa nilai Press’Q sebesar 9,68 > χ⅛0,05) = 3,84, dapat disimpulkan bahwa keakuratan pengklasifikasian terhadap kelompok berdasarkan Indikator tinggi badan menurut umur dianggap konsisten secara statistik untuk data Training.
Tabel 10. Hasil Klasifikasi Balita Sesuai dengan Fungsi Diskriminan untuk Data Testing
|
Status |
Predicted Group Membership |
Total | |||
|
Stunting |
Normal | ||||
|
Original |
Count |
Stunting |
0 |
6 |
6 |
|
Normal |
0 |
17 |
17 | ||
|
% |
Stunting |
0 |
100.0 |
100.0 | |
|
Normal |
01 |
100.0 |
100.0 | ||
Pada Tabel 10 dapat dilihat bahwa balita yang tepat diklasifikasikan sebagai kelompok normal pada data Testing sebanyak 17 orang, sedangkan yang salah diklasifikasikan sebagai “kelompok Stunting” tidak ada. Kemudian balita yang tepat diklasifikasikan sebagai kelompok stunting yaitu tidak ada, sedangkan yang salah diklasifikasikan sebagai “kelompok normal” yaitu 6 orang.
Evaluasi kesalahan dalam Pengklasifikasian untuk data Testing akan diukur menggunakan APPER sebagai berikut:
f 0 + 6\
APPER = I —I × 100% = 26%
Nilai APPER yang diperoleh untuk data Testing menyatakan bahwa fungsi Diskriminan yang terbentuk memiliki tingkat kesalahan klasifikasi sebesar 26% yang berarti bahwa tingkat ketepatan klasifikasi sebesar 74%.
Kemudian dilakukan pengujian kestabilan klasifikasi untuk data Training menggunakan nilai Press’s Q
Dapat dilihat bahwa nilai Press’Q sebesar 5,26 yang kemudian dibandingkan dengan nilai dari table χ2 yaitu χ⅛0,05) = 3,84 yang menyatakan bahwa nilai Press’Q sebesar 5,26 > χ(1;0,05) = 3,84, maka dapat disimpulkan bahwa keakuratan pengklasifikasian terhadap kelompok berdasarkan Indikator tinggi badan menurut umur dianggap konsisten secara statistik untuk data Testing.
Berdasarkan analisis yang telah dilakukan dapat diambil kesimpulan sebagai berikut:
-
1. Model yang terbentuk pada
pengklasifikasian status gizi balita menggunakan analisis diskriminan yaitu keadaan gizi stunting dan normal pada balita dapat ditentukan berdasarkan berat badan lahir seorang balita, dimana setiap penambahan berat badan lahir sebesar 1gram akan mengurangi kemungkinan seorang balita dikelompokkan kedalam kelompok stunting.
-
2. Berat badan lahir (X3), merupakan faktor yang paling berpengaruh dan sebagai penentu seorang balita dapat
dikelompokkan kedalam kelompok stunting dan normal.
-
3. Model Diskriminan yang terbentuk pada pengklasifikasian status gizi balita dapat meningkatkan tingkat ketepatan
klasifikasi sebesar 74 %.
Berdasarkan hasil penelitian diharapkan, bagi ibu hamil agar mengkonsumsi makanan-makanan bergizi dan mengurangi konsumsi makanan yang tidak sesuai dengan kebutuhan gizi. Hal ini dilakukan untuk menghindari terjadinya berat badan lahir rendah yang dapat menyebabkan seorang balita dapat dikategorikan sebagai kelompok stunting
karena berat badan lahir bayi merupakan cerminan dari status gizi ibu saat hamil, apabila berat badan lahir normal berarti status gizi ibu saat hamil baik begitu pula sebaliknya apabila berat badan lahir rendah berarti kondisi gizi ibu saat hamil buruk yang dapat mengakibatkan seorang balita menjadi stunting.
DAFTAR PUSTAKA
Hardle, W. 1990. “Applied Nonparametric
Regression”. New York: Cambridge
University Press.
Hair Jr, J.F., Black, W .C., Babin, B.J. and Anderson, R.E. 2010. “Multivariate Data Analysis”, United States of America:
PEARSON.
Johnson, R. A, and Winchen, D.W. 2007.“Applied Multivarite Statistical
Analysis”. USA: Prentice Hall, Inc.
Maulidya, Dkk. 2014. “Perbandingan Analisis Diskriminan dan Analisis Logistik’. Jurnal Mahasiswa UNESA, 3(1).
MCAIndonesia.“Stunting dan Masa Depan Indonesia”.Millenium Change Account Indonesia.
Suciari, L. Sri. 2015. “Hubungan Antara Status Gizi Ibu Saat Hamil, Panjang Badan, Berat Badan Lahir dan Umur Awal Pemberian MP-ASI”. Tugas Akhir.Fakultas
Kedokteran, Jurusan Ilmu Kesehatan
Masyarakat, Universitas Udayana
30
Discussion and feedback