ANALISIS PERBANDINGAN METODE EXPONENTIAL APPROACH DAN METODE IMPROVED ZERO POINT UNTUK MEMINIMUMKAN BIAYA PENDISTRIBUSIAN
on
E-Jurnal Matematika Vol. 11(3), Agustus 2022, pp. 174-183
DOI: https://doi.org/10.24843/MTK.2022.v11.i03.p378
ISSN: 2303-1751
ANALISIS PERBANDINGAN METODE EXPONENTIAL APPROACH DAN METODE IMPROVED ZERO POINT UNTUK MEMINIMUMKAN BIAYA PENDISTRIBUSIAN
Ni Kadek Jiantari1§, G.K. Gandhiadi2, Ratna Sari Widiastuti3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ayujiantari123@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: gandhiadi@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ratnasariwidiastuti@unud.ac.id]
§Corresponding Author
ABSTRACT
The purpose of this study is to do a comparative of the minimum cost of distributing mountea drinks using the exponential approach and the improved zero point method. The exponential approach method is a direct method where the allocation in this method depends on the number of zeros that appear in the transportation table. In the case of an unbalanced transportation problem, a dummy line (column) will appear where the cost on the line (column) is zero, which will greatly affect the optimum results of the given exponential approach method. The improved zero point method is an improved method from the zero point method, which is very useful for solving all types of transportation problems. This method provides an optimal solution without the help of other modified methods. Based on the results of the research, it was shown that the distribution cost of mountea drinks from the wholesale center in the Lunyuk sub-district using an exponential approach and an improved zero point obtained a cost of 10,392,276 Rupiah before the optimization, while the while the comparative distribution cost of the mountea drinks from the wholesale center in the Lunyuk sub-district after the optimization using an exponential approach and an improved zero point obtained a cost same of 8.552.560 Rupiah.
Keywords: Minimum distribution cost, exponential approach method, improved zero point method.
-
1. PENDAHULUAN
Menurut Kamus Besar Bahasa Indonesia (2021), grosir merupakan pedagang yang melakukan kegiatan pembelian barang dalam kuantitas yang besar dan menjualnya dalam kuantitas yang lebih sedikit pada pihak pengecer atau pada pengguna komersial yang tidak melakukan penjualan dengan volume yang sama pada konsumen tingkat akhir. Grosir adalah saluran distribusi yang kedua atau ketiga setelah distributor. Grosir hanya memiliki gudang dan toko, karyawan penjualan, karyawan gudang dan kasir (Ismail, 2013).
Pusat grosir di Kecamatan Lunyuk terdiri dari Toko UD. Oka Jaya, Toko Cantika, dan Toko Caca. Ketiga pusat grosir tersebut mempunyai kegiatan mendistribusikan produk minuman, beras, obat-obatan pertanian, pupuk, bahan sembako ke berbagai desa sebagai salah satu bagian dari operasional usaha. Dalam mendistribusikan produk tentunya membutuhkan biaya yang tidak sedikit
jumlahnya, maka diperlukan perencanaan yang matang agar biaya transportasi yang dikeluarkan seefisien mungkin.
Secara umum permasalahan yang dihadapi oleh pusat grosir di Kecamatan Lunyuk adalah besarnya biaya pendistribusiaan produk dari beberapa pusat grosir ke beberapa toko konsumen di Kecamatan Lunyuk, khususnya untuk produk Minuman Mountea. Pendistribusian produk minuman mountea dalam proses pendistribusian belum menerapkan konsep transportasi secara matematis untuk pemecahan masalah tersebut.
Strategi dan perencanaan yang baik diperlukan untuk dapat menghemat biaya transportasi dan memperoleh peningkatan keuntungan karena mampu meminimumkan total biaya transportasi serta dapat memenuhi permintaan pasar dengan baik. Sehingga diperlukan metode yang tepat untuk mendistribusikan produk dari sejumlah pusat
grosir ke beberapa tempat tujuan distribusi (Syaifuddin, 2011).
Distribusi merupakan salah satu masalah yang dihadapi oleh pusat grosir di Kecamatan Lunyuk. Permasalahan pendistribusian tersebut menyangkut bagaimana pendistribusian dilakukan dari gudang ke titik-titik distribusi yang ditunjuk pada tiap-tiap daerah. Dalam pendistribusiannya terdapat masalah transportasi yang berkaitan dengan pemilihan rute (jalur) pengangkutan yang mengakibatkan biaya total dari pengangkutan minimum.
Masalah transportasi adalah masalah dengan fungsi objektif meminimumkan biaya transportasi untuk suatu komoditas tertentu dari sejumlah sumber komoditas ke sejumlah tempat tujuan pengiriman komoditas. Kasus transportasi timbul ketika suatu perusahaan ingin mencari cara agar pendistribusian produk dari suatu lokasi ke beberapa sumber dapat meminimumkan biaya. Oleh karena itu, salah satu cara untuk mengatasi masalah distribusi adalah dengan menggunakan metode transportasi (Septiana dkk., 2017).
Metode transportasi merupakan suatu metode yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan produk yang sama ke tempat-tempat yang membutuhkan secara optimal sehingga biaya distribusi yang dikeluarkan adalah minimum. Terdapat beberapa metode yang dapat digunakan untuk mencari solusi yang layak awal yaitu Least Cost (LC), North West Corner Method, dan Vogel Approximation Method (VAM). Setelah solusi layak awal didapat, maka langkah selanjutnya adalah uji optimalitas dengan metode Stepping Stone atau metode MODI (Syaifuddin, 2011). Kelemahan dari serangkaian metode tersebut adalah dalam penyelesaiannya memiliki dua proses penyelesaian sehingga metode ini dipandang kurang efisien.
Seiring perkembangan waktu, muncul beberapa metode baru yang lebih efisien dalam memecahkan masalah transportasi. Metode-metode baru tersebut memiliki perhitungan dengan sedikit langkah dan mudah dipahami. Metode tersebut disebut metode langsung karena langsung mendapatkan solusi optimal tanpa mencari solusi layak awalnya terlebih dahulu. Beberapa metode langsung telah berhasil memberikan solusi optimal pada masalah transportasi seimbang, sedangkan untuk masalah transportasi tidak seimbang belum tentu menghasilkan solusi optimal. Salah
satu metode langsung tersebut adalah metode Exponential Approach yang diusulkan oleh Vannan dan metode Improved Zero Point yang diusulkan oleh Samuel (Basriati dkk., 2019).
Metode Exponential Approach merupakan salah satu metode yang memberikan solusi bagaimana cara pengalokasian barang yang tepat dengan biaya minimum dan metode yang lebih sederhana serta mudah dipahami. Pengalokasian pada metode ini bergantung pada angka nol yang muncul pada tabel transportasi. Pada kasus transportasi tidak seimbang akan muncul baris (kolom) dummy dimana biaya pada baris (kolom) tersebut bernilai nol yang sangat berpengaruh pada hasil optimum yang diberikan oleh metode Exponential Approach sehingga metode ini masih memiliki kelemahan pada masalah transportasi tidak seimbang (Vannan & Rekha, 2013). Metode Improved Zero Point merupakan sebuah metode perkembangan dari metode Zero Point yang sangat berguna untuk memecahkan semua jenis masalah transportasi, metode ini memberikan solusi optimal tanpa bantuan dari metode modifikasi lainnya. Metode ini ditingkatkan dengan metode yang lebih sederhana, efisien, dan mudah dimengerti (Samuel, 2012).
Penelitian sebelumnya berkaitan dengan masalah biaya angkut transportasi dilakukan oleh Fitri, dkk (2019) mengenai perbandingan metode ASM, Stepping Stone, dan metode MODI pada biaya angkut transportasi (studi kasus: data pendistribusian Raskin Perum Bulog Divre Kalimantan Barat). Tujuan dari penelitian tersebut adalah untuk menentukan biaya distribusi yang minimum. Hasil penelitian menunjukkan perbandingan antara ketiga metode untuk menghasilkan biaya yang lebih minimum.
Penelitian lain juga dilakukan oleh BB, Halimatussa’diyah (2018) mengenai perbandingan metode stepping stone dan metode RDI untuk meminimumkan biaya pendistribusian (studi kasus: PT. MEGA ELTRA Medan). Tujuan dari penelitian tersebut adalah untuk menentukan biaya distribusi yang minimum. Hasil penelitian menunjukkan perbandingan antara dua metode untuk menghasilkan biaya transportasi pendistribusian produk semen yang lebih minimum.
Berdasarkan uraian dari latar belakang tersebut, peneliti berkeinginan melakukan penelitian yang berjudul “Analisis Perbandingan Metode Exponential Approach dan Metode Improved Zero Point untuk Meminimumkan
Biaya Pendistribusian (Studi Kasus: Pusat Grosir di Kecamatan Lunyuk)”.
-
2. METODE PENELITIAN
Penelitian ini menggunakan data sekunder dalam bentuk data kuantitatif yaitu berupa data rata-rata jumlah permintaan, jumlah persediaan, dan tarif angkut (biaya transportasi) yang berhubungan dengan pendistribusian Minuman Mountea pada pusat grosir di Kecamatan Lunyuk (Toko UD Oka Jaya, Toko Cantika, dan Toko Caca). Data yang digunakan adalah data rata-rata dalam tiga bulan pada bulan September, Oktober, dan November 2021. Adapun tahapan penyelesaiaan dalam penelitian ini yaitu:
-
1. Pengumpulan data-data untuk digunakan dalam model transportasi. Sumber = Pusat grosir di Kecamatan Lunyuk = Sm;
m = 1,2,3
Daerah tujuan = Desa Sukamaju (T1), Desa Lunyuk Ode (T2), Desa Jamu (T3), Desa Emang Lestari (T4), dan Desa Padasuka (T5).
-
2. Melakukan pemodelan matriks transportasi
Tabel 1. Matriks Transportasi
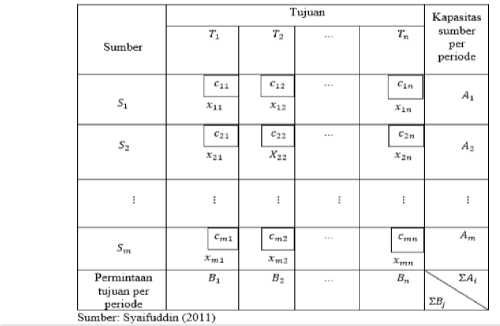
Dengan:
bij, = Biaya distribusi minuman mountea per dus dari sumber m ke tujuan n. Bagian ini memuat metode penelitian yang digunakan untuk mencapai hasil penelitian.
xij = Jumlah minuman mountea yang diangkut per dus dari sumber m ke tujuan n.
-
3. Pembentukan Solusi Optimal Menggunakan Exponential Approach Method.
-
1) a. Membuat tabel transportasi
-
b. Jika tidak seimbang, mengubahnya menjadi seimbang.
-
2) a. Kurangi setiap entri baris dari tabel transportasi dari baris minimum masing-masing.
-
b. kurangi setiap entri kolom dari tabel transportasi dari minimum kolom terkait
-
3) a. Pilih nol pertama pada sel ij dalam tabel yang terjadi dalam matriks biaya. Hitung jumlah total nol tidak termasuk yang dipilih di baris dan kolom yang sesuai.
-
b. tetapkan hukuman eksponensial (jumlah nol di baris dan kolom masing-masing). Ulangi prosedur untuk semua nol dalam matriks.
-
4) a. Sekarang pilih nol dengan mana hukum eksponensial minimum ditetapkan dari langkah 3 dan alokasikan masing-masing nilai sel dengan jumlah maksimum yang mungkin.
-
b. Jika terjadi nilai penalti eksponen sama untuk setiap sel maka pertama memeriksa nilai permintaan dan persediaan,
menghitung nilai rata-ratanya dan
menetapkan alokasi untuk nilai rata-rata yang terendah.
-
5) Hapus baris atau kolom (dimana persediaan atau permintaan menjadi nol) untuk perhitungan lebih lanjut.
-
6) Periksa apakah matriks yang dihasilkan memiliki setidaknya satu nol di setiap kolom dan di setiap baris. Jika tidak ulangi langkah 2, jika iya lanjutkan ke langkah 7.
-
7) Ulang langkah 3 hingga langkah 6 sampai dan kecuali semua permintaan dipenuhi dan semua persediaan habis.
-
8) Untuk nilai yang dialokasikan, hitunglah biaya optimal.
-
4. Pembentukan solusi optimal menggunakan Improved Zero Point Method.
-
1) a. Membuat tabel transportasi
-
b. Jika tidak seimbang, mengubahnya menjadi seimbang.
-
2) a. Jika kolom (baris) dummy ditambahkan, kurangi setiap entri kolom (baris) dari
minimum kolom (baris) masing-masing.
-
b. Dalam matriks yang diturunkan
diperoleh dari 2a, mengganti biaya dummy dengan biaya yang terbesar dari
tabel yang sudah direduksi sebelumnya.
-
3) a. Temukan elemen terkecil dari setiap baris pada nilai tabel dan kemudian kurangi itu dari setiap elemen dari baris.
-
b. Temukan elemen terkecil dari setiap kolom dan kemudian kurangi itu dari setiap elemen dari kolom.
-
4) a. Mengecek apakah setiap kolom permintaan kurang dari atau sama dengan jumlah baris-baris persediaan yang menyuplai kolom permintaan tersebut, dimana baris yang menyuplai adalah baris pada kolom tersebut yang biaya tereduksinya nol.
-
b. Mengecek apakah setiap baris persediaan kurang dari atau sama dengan jumlah kolom-kolom permintaan yang meminta persediaan, dimana kolom yang meminta persediaan adalah kolom pada baris tersebut yang biaya tereduksinya nol.
-
c. Apabila syarat tersebut terpenuhi, langsung menuju langkah 7.
-
5) Menutup semua elemen nol dengan garis mendatar dan tegak seminimal mungkin sehingga beberapa elemen dari kolom-kolom atau baris-baris yang tidak memenuhi syarat pada langkah 4 tidak tertutup.
-
6) a. Menemukan nilai biaya tereduksi yang terkecil pada tabel yang tidak tertutup garis b. Mengurangkan nilai tersebut ke semua elemen nilai yang tidak tertutup garis dan menambahkan nilai tersebut ke semua elemen nilai yang tertutup oleh dua garis. Elemen dalam sel tertutup oleh satu baris tetap tidak berubah.
-
c. Kemudian lanjut ke langkah 4.
-
7) Memilih sel pada tabel transportasi hasil langkah-langkah di atas yang memiliki biaya tereduksi terbesar dan dinamakan (i,j). Jika terdapat lebih dari satu sel, maka dipilih salah satu.
-
8) Memilih sel pada baris atau kolom pada tabel transportasi yang memiliki biaya tereduksi nol dan mengisikan semaksimum mungkin pada sel tersebut sehingga memenuhi persediaan dan permintaan
-
9) Membentuk kembali tabel transportasi yang telah diperbaiki.
-
3. HASIL DAN PEMBAHASAN
-
3.1 Data Penelitian
-
-
a. Sumber dan stok minuman mountea Berikut tiga pusat grosir di Kecamatan Lunyuk yang merupakan sumber penyedia stok minuman mountea:
Tabel 2. Rata-Rata Persediaan Minuman Mountea di Masing-Masing Pusat Grosir
|
Sumber |
Persediaan. Rata-Rata (Dus) |
|
Oka Jaya |
4.871 |
|
Caca |
4574 |
|
Cantika |
5.693 |
|
Jumlah |
15.139 |
Sumber: Data Diolah (2022)
-
b. Daerah tujuan pendistribusian dan permintaan minuman mountea
Pusat grosir di Kecamatan Lunyuk memiliki lima desa tujuan pengiriman dengan permintaan masing-masing yaitu:
Tabel 3. Desa Tujuan Pengiriman dengan Jumlah Rata-Rata Permintaan
|
Tujuan |
Jumlah Rata-Rata (Dus) |
|
Sukamaju |
3.294 |
|
Lunvuk Ode |
3.591 |
|
Jamu |
2.323 |
|
Emang Lestari |
2.509 |
|
Padasuka |
3.421 |
|
Total P er mintaan |
15.139 |
Sumber: Data Diolah (2022)
Diperoleh juga rata-rata biaya distribusi minuman mountea per hari, banyak kegiatan pengiriman, dan jumlah total minuman mountea yang dikirim ke setiap daerah tujuan seperti pada Tabel 4, Tabel 5, dan Tabel 6.
Tabel 4. Rata-Rata Biaya Distribusi Minuman Mountea per Hari, Banyak Kegiatan Pengiriman, dan Jumlah Total Minuman Mountea yang Dikirim ke Setiap Daerah Tujuan Bulan September 2021
Tabel 6. Rata-Rata Biaya Distribusi minuman Mountea per Hari, Banyak Kegiatan Pengiriman, dan Jumlah Total Minuman Mountea yang Dikirim ke Setiap Daerah Tujuan Bulan November 2021
|
Sumber |
Tempat Tujuan |
Banyak Pengiriman (kali) |
Biaya Per Mobil Truk α⅛ι |
Jumlah Mountea (Dus) |
|
Oka Jaya |
Sukamaju |
15 |
Rp72.000 |
1.200 |
|
Lunvuk Ode |
O |
Rp60.000 |
O | |
|
Jamu |
10 |
Rp66.000 |
900 | |
|
Emang Lestari |
9 |
Rp84.000 |
900 | |
|
Padasuka |
20 |
Rp78.000 |
2.000 | |
|
Caca |
Sukamaju |
15 |
Rp72.000 |
1.250 |
|
Lunvuk Ode |
20 |
Rp60.000 |
1.800 | |
|
Jamu |
5 |
Rp66.000 |
540 | |
|
Emang Lestari |
4 |
Rp84.000 |
350 | |
|
Padasuka |
14 |
Rp78.000 |
1.200 | |
|
Cantika |
Sukamaju |
20 |
⅛72.000 |
1.900 |
|
Lunvuk Ode |
20 |
Rp60.000 |
1.890 | |
|
Jamu |
12 |
Rp66.000 |
800 | |
|
Emang Lestari |
15 |
Rp84.000 |
1.300 | |
|
Padasuka |
16 |
Rp78.000 |
1.900 |
|
Sumber |
Tempat Tujuan |
Banyak Pengiriman (kali) |
Biaya Per Mobil Truk (Xp) |
Ijumlali Mountea (Dus) |
|
Oka Jaya |
Sukamaju |
14 |
Rp72.000 |
1.320 |
|
Lunyuk Ode |
12 |
Rp60.000 |
1.230 | |
|
Jamu |
IS |
Rp66.000 |
1.500 | |
|
Emang Lestari |
9 |
Rp84.000 |
810 | |
|
Padasuka |
5 |
R.P78.0O0 |
424 | |
|
Caca |
Sukamaju |
O |
Rp72.000 |
O |
|
Lunvuk Ode |
12 |
Rp60.000 |
860 | |
|
Jamu |
10 |
RpS6.∞0 |
SSO | |
|
Emang Lestari |
6 |
Rp84.000 |
650 | |
|
Padasuka |
20 |
E⅛7S.∞0 |
1.840 | |
|
Cantika |
Sukamaju |
15 |
Rp72.000 |
1.450 |
|
Lunvuk Ode |
12 |
Rp60.000 |
760 | |
|
Jamu |
8 |
Rp66.000 |
950 | |
|
Emang Lestari |
6 |
Rp84.000 |
670 | |
|
Padasuka |
O |
Rp 78.OOO |
O |
Tabel 5. Rata-Rata Biaya Distribusi minuman Mountea per Hari, Banyak Kegiatan Pengiriman, dan Jumlah Total Minuman Mountea yang Dikirim ke Setiap Daerah Tujuan Bulan Oktober 2021
|
Sumber |
Tempat Tujuan |
Banyak Pengiriman (kali) |
Biaya per Mobil Truk α⅛ι |
Jumlah Mountea (Dus) |
|
Oka Jaya |
Sukamaju |
O |
RpO |
O |
|
Lunymk Ode |
19 |
Rp 50. OOO |
1.954 | |
|
Jamu |
6 |
Rp66.000 |
1.200 | |
|
Emang Lestari |
12 |
Rp 84. OOO |
1.176 | |
|
Padasuka |
O |
Rp 78. OOO |
O | |
|
Caca |
Sukamaju |
IS |
Rp 72. OOO |
1.562 |
|
Lunvuk Ode |
8 |
Rp60.000 |
880 | |
|
Jamu |
O |
Rp 5 6. OOO |
O | |
|
Emang Lestari |
5 |
Rp 84. OOO |
810 | |
|
Padasuka |
12 |
Rp 78. OOO |
1.300 | |
|
Cantika |
Sukamaju |
12 |
Rp 72. OOO |
1.200 |
|
Lunvuk Ode |
IS |
Rp60.000 |
1.400 | |
|
Jamu |
6 |
Rp 5 6. OOO |
400 | |
|
Emang Lestari |
10 |
Rp 84. OOO |
860 | |
|
Padasuka |
20 |
Rp 78.000 |
1.600 |
Berdasarkan rata-rata biaya yang dikeluarkan per hari seperti pada Tabel 4, Tabel 5, dan tabel 6 dapat diketahui rata-rata biaya per dus pengiriman minuman mountea (Cif) dengan rincian seperti pada Tabel 7. Biaya per unit atau biaya per dus dapat dihitung dengan membagi biaya total dengan jumlah unit (Horngren, et all., 2012).
Tabel 7. Rata-Rata Biaya Minuman Mountea dalam Tiga Bulan per Unit (Dus)
|
Toko Grosir |
Tujuan |
Biaya Rata-rata per dus (Rp) |
|
Oka Jaya |
Sukamaiu |
Rp555 |
|
LuiLvuk Ode |
Rp390 | |
|
Jamu |
RpdlS | |
|
Emane Lestari |
RpS 7 7 | |
|
Paclaiuka |
Rp567 | |
|
Caca |
Sukamaju |
Rp565 |
|
Lunvuk Ode |
Rp6S3 | |
|
Jamu |
Rp527 | |
|
Emails Lestari |
Rp751 | |
|
Padasuka |
RpSJd | |
|
Cantika |
Sukamaiu |
Rp741 |
|
Lunvuk Ode |
Rp7S5 | |
|
Jamu |
RpS45 | |
|
Emane Lestari |
RpS99 | |
|
Padasuka |
Rp544 |
Keterangan:
Biaya per unit (Dus) = (banyak kegiatan pengiriman tiap tujuan × biaya per hari : jumlah total minuman mountea yang dikirim ke setiap daerah tujuan).
Berdasarkan dari Tabel 4, Tabel 5, Tabel 6, dan Tabel 7 diperoleh biaya pendistribusian minuman mountea (Rp) sebelum dilakukan optimalisasi dengan metode Exponential Approach dan Improved Zero Point adalah sebagai berikut:
Z = (555) 840 + (390) 1061 + (618) 1200 + (877)
962 + (567) 808 +
-
(565) 937 + (683) 1180 + (527) 407 + (751)
603 + (826) 1447 + (741) 1517 + (785)
1350 + (845) 717 + (899) 943 + (544) 1167 Z = 465.818 + 413.490 + 742.133 + 843.506 + 457.816 + 529.189 + 806.070 + 214.408 + 453.285 + 1.194.863 + 1.123.710 + 1.059.173 + 605.772 + 848.438 + 634.605 Z = Rp10.392.276,00
-
3.2 Pemodelan Matriks Transportasi
-
1. Pemodelan Solusi Optimal Matriks Transportasi
-
a. Menyusun tabel matriks transportasi
Berdasarkan data yang telah diperoleh, dapat dibentuk kedalam matriks transportasi seperti pada Tabel 8.
Tabel 8. Matriks Transportasi Pendistribusian Minuman Mountea
|
Sumbet |
Tujuan |
Petsediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
840 |
1061 |
1200 |
962 |
808 |
4871 |
|
Caca |
937 |
1180 |
407 |
603 |
1447 |
4574 |
|
Cantika |
1517 |
1350 |
717 |
943 |
1167 |
5693 |
|
Permmtaan |
3294 |
3591 |
2323 |
2509 |
3421 |
15.139 |
Pada Tabel 8 memberi pengertian bahwa tabel seimbang. Selanjutnya dapat dibentuk juga matriks transportasi untuk biaya per dus seperti pada tabel 9.
Tabel 9. Matriks Transportasi Biaya per Dus Minuman Mountea
|
Sumber |
Tujuan |
Persediaan | ||||
|
Sukaxnaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
555 |
390 |
618 |
877 |
567 |
4.871 |
|
Caca |
565 |
683 |
527 |
751 |
826 |
4.574 |
|
Cantika |
741 |
785 |
845 |
899 |
544 |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
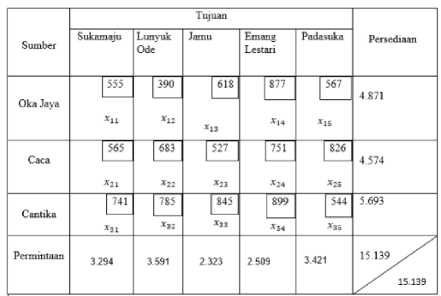
Berdasarkan Tabel 8 dan Tabel 9, maka dapat dibuat tabel matriks transportasi sebelum dilakukan optimalisasi seperti pada Tabel 10.
Tabel 10. Matriks Transportasi Sebelum Dilakukan Optimalisasi
-
b. Membentuk Fungsi Tujuan Minimumkan
Z = (555) %11 + (390) %12 + (618) x13 + (877) x14 + (567) x15 + (565) x21 + (683) x22 + (527) x23 + (751) x24 + (826) x2 5+ (741) x31 + (785) x32 + (845) x33 + (899) x34 + (544) x35
-
c. Membentuk Fungsi Kendala Kendala Persediaan
x11 + x12 + x13 + x14 + x15 = 4.871 x21 + x22 + x23+x24 + x25 = 4.574 x31 + x32 + x33 + x34 + x35 = 5.693
Kendala Permintaan
x11 + x21 + x31 = 3.294 χ12 + x22 + x32 = 3.591 x13 +x23 + x33 = 2-323 x14 + x24 + x34 = 2.509 x15 +x25 + x35 = 3.421 xij ≥ 0,untuk i = 1,2,3 ;j = 1,2,3, ^l6 Berdasarkan data pada Tabel 10, permintaan dan penawaran telah seimbang, sehingga tidak perlu ditambahkan variabel dummy.
-
2. Pembentukan Solusi Optimal dengan Exponential Approach Method
Setelah dibentuk tabel matriks transportasi, selanjutnya dilakukan pengalokasian barang dengan metode Exponential Approach seperti berikut:
Langkah 1 adalah mengurangi setiap elemen dalam baris dengan nilai terkecil, kemudian mengurangi setiap elemen dalam kolom dengan nilai terkecil seperti pada Tabel 11 dan Tabel 12.
Tabel 11. Matriks Transportasi Mountea dengan Reduksi Baris Minimum
|
Sutnbei |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
165 |
0 |
228 |
487 |
177 |
4.871 |
|
Caca |
38 |
156 |
0 |
224 |
299 |
4.574 |
|
Cantika |
197 |
241 |
301 |
355 |
0 |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
Tabel 12. Matriks Transportasi Mountea dengan Reduksi Kolom Minimum
|
Sumber |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
127 |
0 |
228 |
263 |
177 |
4.871 |
|
Caca |
0 |
156 |
0 |
0 |
299 |
4.574 |
|
Cantika |
159 |
241 |
301 |
131 |
0 |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
Langkah 2 adalah Menetapkan hukum eksponensial dari Tabel 12, sehingga diperoleh Tabel 13 berikut:
Tabel 13. Matriks Transportasi dengan Hukum Esponensial
|
Sumber |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
127 |
0® |
228 |
263 |
177 |
4.871 |
|
Caca |
0© |
156 |
o<2) |
OO) |
299 |
4.574 |
|
Cantika |
159 |
241 |
301 |
131 |
o® |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
Langkah 3 adalah Memilih nol dengan hukum eksponensial minimum.
Memilih hukum eksponensial minimum dari Tabel 13 terdapat pada sel (Oka Jaya, Lunyuk Ode) dan (Cantika, Padasuka).
-
a. (4.871 + 3.591)/2 = 4.231
-
b. (5.693 + 3.421)/2 = 4.557
Diperoleh hukum eksponensial minimum terdapat pada sel (Oka Jaya, Lunyuk Ode). Selanjutnya, mengalokasikan nilai pada sel semaksimum mungkin sehingga diperoleh seperti Tabel 14.
Tabel 14. Pengalokasian Nilai pada Sel (Oka Jaya, Lunyuk Ode)
|
Sumber |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
127 |
Oflb 3591 |
228 |
263 |
177 |
4.871 |
|
Caca |
0© |
156 |
0® |
0® |
299 |
4.574 |
|
Cantika |
159 |
241 |
301 |
131 |
Oflb |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
Langkah 4 adalah Setelah langkah 3, hapus kolom dua dari Tabel 14 yang telah dialokasikan nilai sehingga diperoleh Tabel 15.
Tabel 15. Hasil Reduksi dengan Langkah 4
|
Sumber |
Tujuan |
Persediaan | |||
|
Sukamaju |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
127 |
228 |
263 |
177 |
1.280 |
|
Caca |
0 |
0 |
0 |
299 |
4.574 |
|
Cantika |
159 |
301 |
131 |
0 |
5.693 |
|
Permintaan |
3.294 |
2.323 |
2.509 |
3.421 |
15.139 |
Langkah 5 adalah Mengecek apakah setiap baris dan kolom setidaknya ada satu nol. Jika tidak, maka mengulang ke langkah 1. Jika ya, maka lanjut ke langkah 7. Karena di Tabel 4.15 pada baris pertama tidak ada satu nol, maka mengulang ke langkah 1.
Langkah 6 adalah pengulangan langkah 1 – 4 hingga semua permintaan dan persediaan habis.
Berdasarkan Tabel 15, dengan perhitungan yang sama diperoleh solusi optimal Exponential Approach Method dapat dilihat pada Tabel 16.
Berdasarkan Tabel 16 dapat diketahui biaya transportasi optimal metode Exponential Approach yaitu:
Z = (555) 1.280 + (390) 3.591 + (565) 2.014 +
-
(527) 2.323 + (751) 237 + (899) 2.272 +
-
(544) 3.421
= Rp8.552.560,00
Tabel 16. Solusi Optimal Matriks Transportasi Hasil Exponential Approach Pada Distribusi Minuman Mountea

-
3. Pembentukan Solusi Optimal dengan
Improved Zero Point Method
Setelah dilakukan pembentukan solusi optimal dengan metode Exponential Approach, selanjutnya dilakukan pembentukan solusi optimal dengan Improved Zero Point.
Langkah 1 adalah Mengurangi setiap elemen dalam baris dengan nilai terkecil, kemudian mengurangi setiap elemen dalam kolom dengan nilai terkecil seperti pada Tabel 11 dan Tabel 12.
Langkah 2 adalah Mengecek apakah setiap permintaan kurang dari atau sama dengan jumlah baris-baris persediaan yang menyuplai kolom permintaan begitu sebaliknya, dimana baris yang menyuplai adalah baris pada kolom yang bernilai nol. Apabila syarat terpenuhi lanjut ke langkah 6. Dari Tabel 12 dapat diketahui bahwa:
-
a. Permintaan 1 ≤ Persediaan 2
-
b. Permintaan 2 ≤ Persediaan 1
-
c. Permintaan 3 ≤ Persediaan 2
-
d. Permintaan 4 ≤ Persediaan 2
-
e. Permintaan 5 ≤ Persediaan 3
-
f. Persediaan 1 > Permintaan 2
-
g. Persediaan 2 ≤ Permintaan 1 + Permintaan 3 + Permintaan 4
-
h. Persediaan 3 > Permintaan 5
Karena syarat pada Metode Improved Zero Point langkah 2 belum terpenuhi, maka menuju ke langkah 3.
Langkah 3 adalah Semua elemen nol ditutup dengan garis mendatar dan tegak seminimal mungkin sehingga baris atau kolom yang belum terpenuhi tidak tertutup garis. Pilih sel yang tidak tertutup garis yang paling minimum seperti pada Tabel 17.
Tabel 17. Reduksi dengan Langkah 3
|
Sumbei |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
127 |
0 |
228 |
263 |
17? |
4.871 |
|
Q |
156 |
Q |
Q____ |
79 J |
4 >74 | |
|
Cantika |
159 |
241 |
301 |
131 |
0 |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
Kemudian tambahkan nilai sel yang telah dipilih pada sel yang tertutup dua garis dan kurangi pada sel yang tidak tertutup garis. Untuk nilai sel yang tertutup satu garis, nilainya tetap.
Langkah 4 adalah Penutupan nol pada tabel dapat dibentuk tabel perbaikan seperti Tabel 18.
Tabel 18. Hasil Reduksi dengan Langkah 3
|
Sumbei |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
0 |
0 |
101 |
136 |
50 |
4.87 |
|
Caca |
0 |
283 |
0 |
0 |
426 |
4.574 |
|
Cantika |
32 |
241 |
174 |
4 |
0 |
5.693 |
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15.139 |
Langkah 5 adalah pengulangan langkah 2- 4 hingga semua permintaan dan persediaan habis atau terpenuhi.
Langkah 6: Memilih sel dengan biaya tereduksi terbesar pada tabel perbaikan, yaitu biaya tereduksi 430 pada (Caca,Padasuka).
Langkah 7: Selanjutnya, pengisian pertama adalah pada sel yang terletak pada baris ke-2 atau kolom ke-5 yang terlihat hanya memiliki satu elemen nol sehingga pada (Cantika, Padasuka) dialokasikan 3.421. Selanjutnya, pada baris ke-2 terdapat tiga elemen nol, tetapi pada kolom ke-3 hanya terdapat satu elemen nol, sehingga pada (Caca, Jamu) dialokasikan 2.323 dan selanjutnya memilih biaya tereduksi terbesar untuk mengisi sel pada (Caca, Sukamaju) dan (Caca, Emang Lestari) dan dengan cara yang sama untuk semua pengisian pada nilai tereduksi nol diperoleh Tabel 19.
Tabel 19. Pengalokasian Nilai Pada Sel
|
Sutnber |
Tujuan |
Persediaan | ||||
|
Sukamaju |
Lunyuk Ode |
Jamu |
Emang Lestari |
Padasuka | ||
|
Oka Jaya |
1.280 |
3.591 |
4.871 | |||
|
Caca |
2.014 |
2.323 |
237 |
4.574 | ||
|
Cantika |
2.272 |
3.421 |
5.693 | |||
|
Permintaan |
3.294 |
3.591 |
2.323 |
2.509 |
3.421 |
15 139 |
Berdasarkan Tabel 19, diperoleh solusi optimal Improved Zero Point dapat dilihat pada Tabel 20.
Tabel 20. Solusi Optimal Metode Transportasi Hasil Improved Zero Point Method Pada Distribusi Minuman mountea
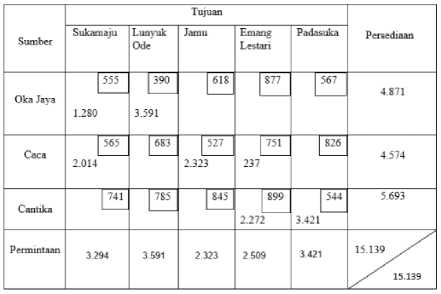
Berdasarkan Tabel 20 dapat diketahui biaya transportasi optimal metode Improved Zero Point yaitu:
Z = (555) 1.280 + (390) 3.591 + (565) 2.014 + (527) 2.323 + (751) 237 + (899) 2.272 + (544) 3.421
= Rp8.552.560,00
-
4. KESIMPULAN DAN SARAN
-
4.1 Kesimpulan
-
Berdasarkan hasil dan pembahasan yang telah dijelaskan, diperoleh kesimpulan sebagai berikut:
-
1. Pada metode Exponential Approach diperoleh biaya distribusi minuman mountea yang minimum dengan proses iterasi yang lebih banyak.
-
2. Pada metode Improved Zero Point diperoleh juga biaya distribusi minuman mountea yang minimum tetapi dengan proses iterasi yang lebih sedikit.
-
3. Hasil perbandingan biaya minimum dengan menggunakan metode Exponential Approach dan Improved Zero Point dari tiga toko grosir di Kecamatan Lunyuk ke lima desa tujuan pengiriman menghasilkan biaya yang sama sebesar 8.552.560 rupiah. Biaya tersebut lebih rendah dari pada biaya yang harus dikeluarkan toko grosir untuk
pendistribusian minuman mountea sebelum menggunakan metode Exponential Approach dan Improved Zero Point. Dengan kata lain, terjadi penghematan biaya pendistribusian minuman mountea sebesar 18% atau Rp1.839.716,00.
-
4.2 Saran
Berdasarkan kesimpulan di atas peneliti dapat memberikan saran untuk dianjurkan kepada toko grosir di Kecamatan Lunyuk dimana untuk Toko UD Oka Jaya hanya mendistribusikan produk minuman mountea ke Desa Sukamaju dan Desa Lunyuk Ode, Toko Caca hanya ke Desa Sukamaju, Desa Jamu dan Desa Emang Lestari, dan Toko Cantika hanya ke Desa Emang Lestari dan Desa Padasuka agar menghemat biaya pendistribusian.
DAFTAR PUSTAKA
Basriati, S., Safitri, E., & Yustari, W. (2019). Aplikasi Metode Improved Exponential Approach untuk Mendapatkan Solusi
Optimum Pendistribusian Komoditas ( Studi Kasus: PT. Tirta Sumber Mekarsari ). Jurnal Sains Matematika Dan Statistika, 5(2), 119–128.
Halimatussa’diyah, BB. (2018). Perbandingan Metode Stepping Stone Dan Metode Revised Distribution (RDI) Untuk Meminimumkan Biaya Pendistribusian (Studi Kasus: PT. Mega Eltra Cabang Medan). Skripsi. Universitas Sumatera Utara. Medan.
Fitri, Helmi, & Kiftiah, M. (2019). Perbandingan Metode ASM, Stepping Stone dan Metode MODI Pada Biaya Angkut Transportasi (Kasus Studi: Data
Pendistribusian Raskin Perum Bulog Divre Kalimantan Barat Tahun 2018 Pada Bulan Januari-September). Bimaster: Buletin
Ilmiah Matematika, Statistika Dan Terapannya, 8(2), 387–392.
https://doi.org/10.26418/bbimst.v8i3.33172
Grosir Pada KBBI Daring. (2021).
Horngren, C. T., Datar, S. M., & Rajan, M. (2012). Cost Accounting: A Managerial Emphasis,. In Issues in Accounting Education.
https://doi.org/10.2308/iace.2010.25.4.789
Ismail, A. (2013). Peran Value Chain Pada Pedagang Grosir Dalam Hubungannya Strategy Pemasaran. BENEFIT Jurnal Manajemen dan Bisnis, 17(1), 1–8.
Samuel, A. E. (2012). Improved zero point method (IZPM) for the transportation problems. Applied Mathematical Sciences, 6(109–112), 5421–5426.
Septiana, A. R., Ratnasari, L., & Solikhin.
-
(2017) . Metode Asm Pada Masalah Transportasi Seimbang. Matematika, 20(2), 71–78.
Syaifuddin, D. T. (2011). RISET OPERASI (Aplikasi Quantitative Analysis for Management) (Sujono (Ed. 1)). Percetakan CV Citra Malang.
Vannan, S. E., & Rekha, S. (2013). A New Method for an Optimal Solution for
Transportation Problems. International
Journal of Engineering and Advanced Technology (IJEAT), 2(5), 369–371.
183
Discussion and feedback