METODE ANALISIS REGRESI SPASIAL DALAM MEMODELKAN KASUS COVID-19 DI INDONESIA
on
E-Jurnal Matematika Vol. 11(3), Agustus 2022, pp. 167-173
DOI: https://doi.org/10.24843/MTK.2022.v11.i03.p377
ISSN: 2303-1751
METODE ANALISIS REGRESI SPASIAL DALAM MEMODELKAN KASUS COVID-19 DI INDONESIA
Ni Made Puspasari1§, Ni Luh Putu Suciptawati2, Made Susilawati3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: puspasarimade1302@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: suciptawati@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@unud.ac.id]
§Corresponding Author
ABSTRACT
Covid-19 is an infectious disease caused by Severe Acute Respiratory Syndrome Coronavirus 2. The transmission of Covid-19 has negative impact on every aspect. This study aimed to determine the factors that significantly affect the number of Covid-19 cases in Indonesia. Spatial regression analysis was used as the research method. The results obtained that on the dependent variable there is a spatial dependence, so the selected model is Spatial Autoregressive Model (SAR) with an AIC value of 759.09 and an R2 value of 58.49%. The significant influencing factor is proportion of the population over 50 years old and open unemployment rate.
Keywords: Covid-19, Spatial, and SAR.
Pemodelan data yang memanfaatkan hubungan antara dua peubah kuantitatif dapat dilakukan dengan metode analisis regresi. Terdapat berbagai pengembangan dari metode analisis regresi, salah satunya metode yang mempertimbangkan data dengan pengaruh lokasi atau daerah yaitu analisis regresi spasial. Hukum pertama geografis yang dikemukakan Tobler menyatakan bahwa kondisi lokasi suatu pengamatan dengan lokasi pengamatan lain yang berdekatan memiliki hubungan erat (efek spasial). Model yang terbentuk apabila terdapat efek spasial pada data ialah model regresi spasial (Anselin, 1988). Pemodelan spasial dapat dibagi menjadi dua yaitu pemodelan data berdasarkan pendekatan titik dan area (LeSage, 1999). Berdasarkan pendekatan area, model regresi spasial yang terbentuk di antaranya Spatial Autoregressive Model, Spatial Error Model, dan Spatial Autoregressive Moving Average (Anselin, 1988).
Penelitian terdahulu yang dilakukan oleh (Habinuddin, 2021) dalam memodelkan jumlah kasus Covid-19 di Kota Bandung diperoleh hasil bahwa model yang dipilih adalah Spatial Autoregressive Model (SAR). Variabel yang signifikan berpengaruh adalah jumlah penduduk usia 60 tahun ke atas, jumlah kemiskinan, dan
jumlah penduduk tidak bekerja. Penelitian lain dilakukan oleh (Mahdy, 2020) yang menggunakan metode GWR untuk memodelkan kasus Corona di Jawa Barat. Hasil yang diperoleh adalah koefisien determinasi pada pemodelan kasus Corona di Jawa Barat dengan metode regresi linear lebih kecil dibandingkan dengan metode GWR (Geographically Weighted Regression). Kepadatan penduduk, persentase kemiskinan, tingkat pengangguran terbuka, persentase rumah tangga dengan sanitasi layak, dan persentase rumah tangga dengan sumber air minum yang layak merupakan faktor yang berpengaruh pada penelitian tersebut.
Penyakit menular Coronavirus Disease 2019 (Covid-19) disebabkan oleh Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) (Sugihartono et al., 2019). Berdasarkan laporan Kementerian Kesehatan sampai dengan tanggal 4 April 2021 sebanyak 1.527.524 kasus konfirmasi Covid-19 dan 41.669 kasus meninggal. Jumlah ini meningkat dari minggu sebelumnya. Daerah dengan jumlah kasus konfirmasi tertinggi adalah Provinsi DKI Jakarta, Provinsi Jawa Barat, dan Provinsi Jawa Tengah. Sedangkan daerah dengan jumlah kasus konfirmasi terendah dimiliki oleh Provinsi Maluku Utara (Kementerian Kesehatan, 2021b).
Berbagai dampak merugikan pada setiap aspek kehidupan terjadi akibat penyebaran virus Covid-19 dari suatu lokasi menuju lokasi lainnya yang berlangsung dengan begitu cepat. Diperlukan analisis untuk mengurangi dampak tersebut. Menurut (Mahdy, 2020) penyebaran virus Covid-19 dipengaruhi oleh letak geografis, oleh karena itu digunakan metode analisis regresi spasial untuk memodelkan kasus Covid-19 pada setiap provinsi di Indonesia serta untuk mengetahui faktor yang secara signifikan berpengaruh terhadap jumlah kasus Covid-19 di Indonesia.
Pada penelitian ini, data yang digunakan merupakan data sekunder pada tahun 2020 yang diperoleh dari Badan Pusat Statistik Indonesia. Adapun variabel dependen dalam penelitian ini adalah jumlah kasus Covid-19 di setiap provinsi di Indonesia yang tercatat pada tanggal 1 Agustus 2021 sampai dengan 31 Agustus 2021, serta variabel bebas yang digunakan antara lain kepadatan penduduk, persentase kemiskinan, persentase rumah tangga dengan sanitasi layak, persentase penduduk usia 50 tahun ke atas, dan tingkat pengangguran terbuka di setiap provinsi di Indonesia. Pada penelitian ini digunakan metode analisis regresi spasial. Adapun tahapan dalam analisis adalah sebagai berikut:
-
1. Eksplorasi data dengan peta tematik, sehingga penyebaran setiap variabel dapat diketahui dari sudut kewilayahanya.
-
2. Estimasi Model Regresi Linear dan Uji Asumsi Regresi Linear
Analisis regresi merupakan metode statistik yang memanfaatkan hubungan antara dua peubah kuantitatif. Model umum analisis regresi dinyatakan sebagai berikut (Kurtner et al., 2005).
-
Yi = β0 + βizi,1 +-----+ βk-izi,k-1 + εi (1)
dengan Yi adalah nilai peubah respons dalam amatan ke-i, β0,β1, ., βk-1 adalah parameter, Xi,ι,Xi,2, ■ ,Xi,k-ι adalah nilai peubah bebas dari amatan ke-i, εi adalah suku galat yang saling bebas dan menyebar N(0,σ2}, i adalah amatan (1,2, ..., n), dan k adalah banyaknya parameter.
Model regresi linear sederhana memiliki beberapa asumsi (Gujarati and Porter, 2009), yaitu:
3.
4.
5.
-
a. Varians dari galat adalah konstan atau homoskedastisitas.
-
b. Tidak terdapat autokorelasi
antarsisaan.
-
c. Tidak terdapat multikolinearitas.
-
d. Sisaan dari model yang diestimasi berdistribusi normal.
Membentuk Matriks Pembobot Spasial (W).
Matriks pembobot spasial adalah suatu
matriks simetris berukuran n× n yang menggambarkan kedekatan hubungan antara suatu wilayah dengan wilayah lainnya. Matriks ini terbentuk berdasarkan hubungan ketetanggaan antarlokasi yang digunakan untuk menentukan bobot antarlokasi pengamatan.
Uji Moran’s I
Menurut (Lee and Wong, 2001) untuk mengidentifikasi autokorelasi antar lokasi amatan dapat menggunakan uji Moran’s I. Hipotesis uji:
H0:1 = 0 (tidak ada autokorelasi antar lokasi)
H1:I ≠ 0 (ada autokorelasi antar lokasi)
i-e(i^) √vαr (I)
Statistik uji: Zhiluna
Kriteria keputusan:
tolak
H0 jika
lzKitungl > Za/2.
Uji Lagrange Multiplier Menurut (Anselin, 1988) beberapa jenis uji Lagrange
terdapat Multiplier
(LM), di antaranya:
-
a. Kebergantungan Spasial pada
Variabel Dependen
Hipotesis uji:
H0: p = 0 (tidak ada kebergantungan spasial pada variabel dependen)
H1: p ≠ 0 (ada kebergantungan spasial pada variabel dependen)
[ετWy∕(-)]
Statistik uji: LMlαg = ------n dengan
D
_ I(WXβ)τ(I - X(XτX')-1Xτ)WXβ)∖
= [ σ ]
+ tr(W2 + WτW)
Kriteria keputusan: tolak H0 jika LMlαg>χ2a,ι.
-
b. Kebergantungan Spasial pada Sisaan Hipotesis uji:
H0 : λ = 0 (tidak ada
kebergantungan spasial pada sisaan)
H1: λ ≠ 0 (ada kebergantungan
spasial pada sisaan)
[ετWε∕(⅛
Statistik uji: LMerr = , ,
j err tr(W2+Wτ W)
c.
Kriteria keputusan: tolak H0 jika LMerr > χa,1.
Kebergantungan Spasial pada Variabel
Dependen dan Sisaan
Hipotesis uji:
H0 : p = 0 dan λ = 0 (tidak ada kebergantungan spasial pada variabel dependen dan sisaan)
H1 : p ≠ 0 dan λ ≠ 0 (ada kebergantungan spasial pada variabel dependen dan sisaan)
Statistik uji:
LM(lag,err) = E-1 {(Ry)2T - 2RyT + (Rε)2(D + T)}
-
• ετWy ετWε
dengan Ry = — , Rε = — ,
T = tr{(Wτ + W)W},
D = σ2(Wτ X β)τ M (Wt X β) ,
M = I-X(XtX)-1Xt, dan
E = (D +T)T-(T)2.
Kriteria keputusan: tolak H0 jika
LM (lag, err) > Xa,2.
-
6. Jika terdapat kebergantungan spasial pada variabel dependen, maka dilanjutkan dengan melakukan pemodelan SAR. Model SAR dinyatakan sebagai berikut (Anselin, 1988):
^i = pΣ wijYj + Σ βikxik + εi(2)
-
7. Apabila terdapat kebergantungan spasial pada galat (sisaan), maka dilanjutkan dengan melakukan pemodelan Spatial Error Model (SEM). Definisi model regresi SEM secara umum sebagai berikut (Anselin, 1988):
Yi = ∑βikXik + λ∑wijUj + εi(3)
-
8. Apabila terdapat kebergantungan spasial pada variabel dependen dan galat (sisaan), maka dilanjutkan dengan melakukan pemodelan Spatial Autoregressive Moving Average (SARMA). Definisi model regresi SARMA secara umum sebagai berikut.
y = ∑piWiy + Xβ + ε + ∑λiWiε(4)
-
9. Pemilihan model terbaik dengan melihat nilai AIC (akaike’s information criterion) yang paling kecil dan atau R2 terbesar.
-
10. Uji Signifikansi Pendugaan Parameter
Uji Wald digunakan dalam pengujian signifikansi parameter. (Anselin, 1988) menyatakan bahwa hipotesis uji dari uji Wald tersebut adalah sebagai berikut:
-
a. Hipotesis uji Wald pada model SAR H0 : p = 0 dan β = 0 (parameter
tidak signifikan)
H1 : p ≠ 0 dan β ≠ 0 (parameter
signifikan)
-
b. Hipotesis uji Wald pada model SEM
H0 : λ = 0 dan β = 0 (parameter
tidak signifikan)
H1 : λ≠ 0 dan β ≠ 0 (parameter
signifikan)
-
c. Hipotesis uji Wald pada model SARMA
H0: p = 0, λ=0 dan β = 0
(parameter tidak signifikan)
H1: p≠0, λ≠0 dan β≠0
(parameter signifikan)
Statistik uji: Wald = Q^j) dengan r
merupakan nilai penduga suatu parameter dan
se(r) merupakan standar error dari penduga
parameter r.
Kriteria keputusan: H0 ditolak apabila
Wald > X(a,1) atau p — value < a.
-
11. Interpretasi model terbaik.
Deskripsi Provinsi di Indonesia Berdasarkan Jumlah Kasus Covid-19 serta Faktor-faktor yang Memengaruhinya
Pada penelitian ini, peta tematik digunakan untuk mengetahui penyebaran setiap variabel dari sudut kewilayahan. Berikut tampilan
peta tematik untuk jumlah kasus Covid-19 di Indonesia.
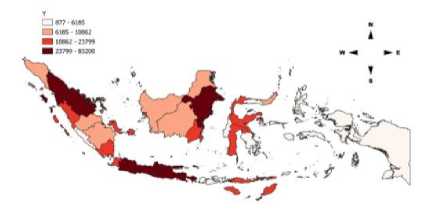
Gambar 1. Peta Tematik Jumlah Kasus Covid-19 di
Indonesia
Berdasarkan Gambar 1 terlihat bahwa semakin gelap warna lokasi pada peta tematik menunjukkan bahwa penyebaran jumlah kasus Covid-19 di Indonesia semakin tinggi. Sebagian besar jumlah kasus Covid-19 tinggi terletak pada provinsi di Pulau Jawa, sedangkan jumlah kasus Covid-19 yang rendah ada pada Provinsi Papua dan provinsi disekitarnya Provinsi yang berdekatan memiliki warna yang sama, sebagaimana disebutkan oleh Tobler pada hukum pertama mengenai hubungan erat yang dimiliki oleh lokasi pengamatan yang berdekatan memiliki hubungan erat (efek spasial).
Estimasi Model Regresi Linear dan Uji Asumsi Regresi Linear
Ordinary Least Square (OLS) merupakan metode yang digunakan pada estimasi parameter model regresi linear sehingga diperoleh hasil sebagai berikut.
Tabel 1. Estimasi Parameter Model Regresi Linear
|
Estimasi Parameter |
Ihitung |
p — value | |
|
A1 |
—6,164 × 104 |
— 1,708 |
0,09868 |
|
Al |
—0,04382 |
— 0,037 |
0,97085 |
|
A2 |
—24,38 |
— 0,037 |
0,97053 |
|
A3 |
—450,6 |
— 1,212 |
0,23551 |
|
A4 |
4518 |
4,794 |
4,88 × 10-5 |
|
β5 |
4868 |
2,899 |
0,00721 |
|
a = 0,05 | |||
|
R2 = 52,02% | |||
|
AIC = 761,1921 | |||
Sumber: Data diolah, 2022
Berdasarkan Tabel 1. jumlah kasus Covid-19 di Indonesia dipengaruhi oleh dua variabel yang signifikan yaitu persentase penduduk usia 50 tahun ke atas dan tingkat pengangguran terbuka, karena memiliki p — value < a. Dengan demikian, estimasi model regresi linear yang diperoleh adalah:
^ = —6,164 × 104 — 0,00004794Z4,i
+ 0,00721Z5,i ' ( )
Selanjutnya untuk melihat kemungkinan ada atau tidaknya efek spasial pada data, dilakukan uji asumsi analisis regresi linear pada Persamaan 5.
Tabel 2. Uji Asumsi Analisis Regresi Linear
|
Hipotesis Uji |
Keputusan | |
|
H0: Sisaan mengikuti sebaran normal H1: sisaan tidak mengikuti sebaran normal |
Z2 = 1,5114 df = 2 p — value = 0,4697 Z20.05;2)= 5,9915 |
H0 diterima |
|
H0: tidak terdapat autokorelasi H1: terdapat autokorelasi |
HMZ = 1,5213 dL = 1,1439 dU = 1,8076 dL ≤ DM ≤ dU |
Pengujian tidak meyakinkan |
|
H0: ragam homogen H1: ragam tidak homogen |
BP = 23,507 df = 5 p — value = 0,0002699 V 2 , Z(0,05;5) = 11,0705 |
H0 ditolak |
|
VIF > 10 Terdapat multikolinearitas |
Z1 = 1,373723 Z2 = 1,661949 Z3 = 1,815624 Z4 = 1,256164 Z5 = 1,515623 |
Tidak terdapat multi-kolinearitas |
Sumber: Data diolah, 2022
Berdasarkan Tabel 2. terlihat bahwa terdapat pelanggaran asumsi. Pada uji homoskedastisitas diperoleh hasil bahwa ragam tidak homogen dan pada uji autokorelasi diperoleh hasil bahwa pengujian tidak meyakinkan sehingga ada kemungkinan terdapat efek spasial pada data. Oleh karena itu, analisis dilanjutkan dengan uji kebergantungan spasial untuk melihat ada tidaknya kebergantungan spasial.
Uji Kebergantungan Spasial
Tabel 3. Uji Moran’s I
|
Moran’s I |
p — value |
|
0,17292921 |
0,07704 |
|
a = |
0,05 |
|
I0 = —0,08463315 | |
Sumber: Data diolah, 2022
Berdasarkan Tabel 3 terlihat bahwa p — value > a, sehingga memperoleh keputusan yaitu tidak cukup bukti untuk menolak H0 yang berarti tidak terdapat autokorelasi antarlokasi. Namun, dapat dilihat bahwa nilai Moran’s I > I0. Hal ini berarti autokorelasi bernilai positif dan membentuk pola mengelompok yang mengindikasikan karakteristik yang sama antarprovinsi yang berdekatan. Untuk melihat autokorelasi pada setiap variabel, maka dilakukan uji Moran’s I pada variabel-variabel yang digunakan.
Analisis dilanjutkan dengan uji LM untuk mengidentifikasi ada tidaknya kebergantungan spasial pada variabel dependen, sisaan, dan atau keduanya.
Tabel 4. Uji Lagrange Multiplier
|
Hipotesis |
Nilai Statistik Uji |
Keterangan |
|
Ho : P = O H1 : p ≠0 |
LMlag = 4,82245 X20,05;i) = 3,8415 p — value = 0,02809 |
H0 ditolak |
|
H0 : λ = 0 H1 : λ ≠ 0 |
LMerr = 1,30932 X‰ι) = 3,8415 p — value = 0,25252 |
H0 diterima |
|
H0 : P = O dan λ = 0 H1 : p ≠ 0 dan λ ≠ 0 |
LMiag,err = 5,39953 Z220,052) = 5.991 p — value = 0,06722 |
H0 diterima |
Sumber: Data diolah, 2022
Berdasarkan Tabel 4. terlihat bahwa terdapat kebergantungan spasial pada variabel dependen. Oleh karena itu, analisis dilanjutkan dengan model analisis regresi SAR.
Pemodelan Regresi SAR
Pendugaan parameter dan pengujian signifikansi pendugaan parameter pada model SAR adalah sebagai berikut (Tabel 5).
Berdasarkan Tabel 5 terlihat bahwa variabel persentase penduduk usia 50 tahun ke atas dan tingkat pengangguran terbuka mempunyai nilai p — value < a, sehingga keputusan yang diperoleh yaitu menolak H0 yang berarti kedua variabel tersebut berpengaruh signifikan terhadap jumlah kasus Covid-19 di Indonesia. Sedangkan variabel kepadatan penduduk, persentase kemiskinan, dan persentase rumah tangga dengan sanitasi layak mempunyai nilai p — value > a, sehingga keputusan yang diperoleh yaitu tidak
dapat menolak H0 yang berarti ketiga variabel tersebut tidak berpengaruh secara signifikan terhadap jumlah kasus Covid-19 di Indonesia.
Tabel 5. Pendugaan Parameter Model SAR dan Uji Wald
|
Parameter |
Estimasi Parameter |
Wald |
p-value |
|
P |
0,25539 |
4,5405 |
0,042819 |
|
β0 |
—44071 |
2,0575 |
0,1514512 |
|
β1 |
—0,40224 |
0,1592 |
0,6899017 |
|
β2 |
—94,380 |
0,0322 |
0,8576184 |
|
β3 |
—397,44 |
1,6370 |
0,2007354 |
|
β4 |
3432,6 |
13,2308 |
0,0002754 |
|
βs |
4059,8 |
7,7609 |
0,0053405 |
|
a = 0,05 | |||
|
R2 = 52,02% | |||
|
AIC = 761,1921 | |||
Sumber: Data diolah, 2022
Model regresi SAR yang terbentuk adalah sebagai berikut.
Y1 = 0,25539WYj — 44071 + 3432,6X4
+ 4059,81X5i (6)
dengan Yi merupakan penduga jumlah kasus Covid-19 pada provinsi ke-i di Indonesia, Yj merupakan jumlah kasus Covid-19 pada provinsi ke-j di Indonesia, W merupakan matriks pembobot spasial, X4i merupakan persentase penduduk usia 50 tahun ke atas pada provinsi ke-i di Indonesia dan X5i merupakan tingkat pengangguran terbuka pada provinsi ke-i di Indonesia.
Pemilihan Model Terbaik
Nilai AIC dan R2 pada model regresi linear dan model SAR yang terbentuk adalah sebagai berikut.
Tabel 6. Nilai AIC dan R2 pada Model Regresi Linear dan SAR
|
Model |
Nilai AIC |
R2 |
|
Regresi Linear |
761,1921 |
52,02% |
|
SAR |
759,09 |
58,49% |
Sumber: Data diolah, 2022
Berdasarkan Tabel 6. terlihat bahwa model dengan AIC terkecil dan R2 terbesar adalah model SAR. R2 dengan nilai 58,49% mengindikasikan bahwa variabel bebas pada model mampu menjelaskan variabel dependen
sebesar 58,49% dan 41,51% lainnya dijelaskan oleh variabel lain di luar model. Nilai R2 pada model terpilih tidak terlalu besar, hal ini dikarenakan faktor-faktor lain di luar model yang diduga signifikan berpengaruh namun belum diikutsertakan dalam penelitian ini. Berdasarkan web resmi Direktorat Jenderal Pencegahan dan Pengendalian Penyakit Kementerian Kesehatan, faktor lain yang dapat mengendalikan penyebaran Covid-19 di antaranya perberlakuan Pembatasan Sosial Berskala Besar (PSBB) di daerah dengan dampak Covid-19 tinggi, disiplin dalam merenapkan protokol kesehatan, dan penguatan sistem kesehatan seperti akses pelayanan kesehatan, infrastruktur, persediaan peralatan medis, dan lain sebagainya (Kementerian Kesehatan, 2021a).
Interpretasi Model Regresi SAR
Model SAR pada Persamaan 6 memiliki interpretasi sebagai berikut:
-
a. Koefisien p = 0,25539 berarti bahwa jika suatu provinsi dikelilingi oleh provinsi lainnya, maka pengaruh dari provinsi disekelilingnya dapat diukur sebesar 0,25539 dikali jumlah kasus Covid-19 di provinsi sekitarnya apabila faktor-faktor lainnya bernilai konstan.
-
b. Koefisien β0 = -44071 berarti bahwa
jumlah kasus Covid-19 di suatu provinsi akan menurun sebesar 44071 kasus apabila faktor-faktor lainnya bernilai nol.
-
c. Koefisien β4 = 3432,6 berarti bahwa jika persentase penduduk usia 50 tahun ke atas di suatu provinsi naik sebanyak satu persen, maka akan menaikkan jumlah kasus Covid-19 di provinsi tersebut sebesar 3432,6 kasus apabila faktor-faktor lainnya bernilai konstan.
-
d. Koefisien β5 = 4059,81 berarti bahwa jika tingkat pengangguran terbuka di suatu provinsi naik sebanyak satu persen, maka akan menaikkan jumlah kasus Covid-19 di provinsi tersebut sebesar 4059,81 kasus apabila faktor-faktor lainnya bernilai konstan.
Dari model SAR pada Persamaan 6 diperoleh model yang berbeda pada setiap provinsi. Oleh karena itu, diperoleh sebanyak 34 model persamaan. Sebagai contoh Provinsi Banten yang memiliki dua tetangga yaitu Provinsi Jawa Barat dan D.K.I. Jakarta, dengan model persamaan sebagai berikut:
^Banten = 0,25539Yjawa Barat + 0,25539YD.K.LJakarta - 44071 + 3432,6⅛nten + 4059,81⅛nten
Interpretasi dari model di atas adalah jumlah kasus Covid-19 di Provinsi Banten dipengaruhi oleh Provinsi Jawa Barat dan D.K.I. Jakarta. Jika jumlah kasus Covid-19 di Jawa Barat dan D.K.I. Jakarta meningkat satu satuan, maka jumlah kasus Covid-19 di Banten juga meningkat sebesar 0,25539.
Kesimpulan
Pada pemodelan jumlah kasus Covid-19 dari setiap provinsi di Indonesia diperoleh bahwa terdapat kebergantungan spasial pada variabel dependen. Sehingga model yang dipilih adalah model SAR dengan nilai AIC sebesar 759,09 dan nilai R2 sebesar 58,49%.
Faktor-faktor yang secara signifikan memiliki pengaruh terhadap jumlah kasus Covid-19 pada setiap provinsi di Indonesia adalah persentase penduduk usia 50 tahun ke atas dan tingkat pengangguran terbuka.
Saran
Dalam penelitian ini, diperoleh nilai R2 yang belum cukup tinggi. Oleh karena itu, disarankan mempertimbangkan variabel independen lain seperti ketersediaan fasilitas kesehatan, mengingat virus yang terus berkembang dan diperlukan penanganan yang cepat.
Selain itu, disarankan untuk mengurangi kegiatan yang berisiko meningkatkan peluang terpapar virus Covid-19, menaati kebijakan pemerintah terkait pemberlakuan pembatasan sosial, dan tetap mematuhi protokol kesehatan.
DAFTAR PUSTAKA
Anselin, L. (1988) Spatial Econometrics:
Methods and Models, Economic
Geography. Netherlands: Kluwer Academic Publishers.
Gujarati, D. N. and Porter, D. C. (2009) Basic Ecomometrics. 5th ed. New York: McGraw-Hill/Irwin.
Habinuddin, E. (2021) ‘Regresi Spasial pada Jumlah Kasus Covid-19 di Kota Bandung’, Jurnal Statistika dan Matematika, 3(2), pp. 175–181.
Kementerian Kesehatan (2021a) Penguatan
Sistem Kesehatan dalam Pengendalian
Covid-19, Kementerian Kesehatan.
Available at:
http://p2p.kemkes.go.id/penguatan-sistem-kesehatan-dalam-pengendalian-covid-19/ (Accessed: 22 April 2022).
Kementerian Kesehatan (2021b) Situasi Global, Situasi Global Di Masa Pandemi Covid -19. Available at:
https://infeksiemerging.kemkes.go.id/categ ory/situasi-terkini (Accessed: 2 April 2021).
Kurtner, M. H., Nachtsheim, C. J., Neter, J., and Li, W. (2005) Applied Linear
Statistical Models. 5th ed. New York: McGraw-Hill/Irwin.
Lee, J. and Wong, D. W. S. (2001) Statiscal Analysis with ArcView Gis. Canada: John
Wiley & Sons Inc.
LeSage, J. P. (1999) The Theory and Practice of Econometrics., Economica. Toledo: Departement of Economics University of Toledo. doi: 10.2307/2553707.
Mahdy, I. F. (2020) ‘Pemodelan Jumlah Kasus Covid-19 Di Jawa Barat Menggunakan Geographically Weighted Regression’, Seminar Nasional Official Statistics, 2020(1), pp. 138–145. doi:
10.34123/semnasoffstat.v2020i1.642.
Sugihartono, A., Burhan, E., Susanto, A. D., Damayanti, T., and Wiyono, H. (2019) Pedoman dan Pencegahan Coronavirus (COVID- 19), Math Didactic: Jurnal Pendidikan Matematika. Kementerian
Kesehatan RI. doi:
10.33654/math.v4i0.299.
173
Discussion and feedback