PEMODELAN ANGKA MORTALITAS IBU DI PROVINSI BALI MENGGUNAKAN METODE REGRESI POISSON
on
E-Jurnal Matematika Vol. 11(1), Januari 2022, pp. 6-11
DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p353
ISSN: 2303-1751
PEMODELAN ANGKA MORTALITAS IBU DI PROVINSI BALI MENGGUNAKAN METODE REGRESI POISSON
Ni Putu Nadya Agusviani1§, I Komang Gde Sukarsa2, Made Susilawati3
1Program Studi Matematika, FMIPA, Universitas Udayana [Email: nadyaputu4@gmail.com]
2Program Studi Matematika, FMIPA, Universitas Udayana [Email: gedesukarsa@unud.ac.id]
3Program Studi Matematika, FMIPA, Universitas Udayana [Email: mdsusilawati@unud.ac.id]
§Corresponding Author
ABSTRACT
Maternal Mortality Rate (MMR) is a metric used to assess a region's maternal health status. Maternal death occurs when a woman dies during pregnancy or until 42 days after to the pregnancy itself or its handling. It does not count if the death occurred as a result of an accident or injury. There are number of factors that cause maternal death, one of which is the direct factor that still dominates up to now on. In this study, MMR modeling in Bali was conducted in 2019 by using 6 factors that are thought to be influential. Poisson Regression method is used to determine the factor that cause maternal death. Based on this study of maternal death rate in Province of Bali, it shows that the percentage of pregnant mother visits K1 (X1) and the percentage of obstetric complication cases (X2) are significant towards the variable.
Keywords: Maternal Mortality Death (MMR), Poisson Regression, Province of Bali
Salah satu tolak ukur untuk menentukan kesehatan ibu di suatu wilayah disebut Angka Mortalitas ibu. Angka Mortalitas Ibu atau yang dikenal dengan Angka Kematian Ibu (AKI) merupakan kematian yang terjadi selama kehamilan hingga hari ke-42 setelah melahirkan. yang diakibatkan pada kehamilan ataupun penanganan dan bukan dikarenakan dari kecelakaan (WHO, UNICEF, 2000). Faktor dari AKI terjadi antara lain belum terlaksananya pemeriksaan continuity of care pada ibu dan adanya kendala persalinan yang tidak segera ditangani (Novarani et al., 2016).
Di seluruh Indonesia Angka Kematian Ibu menjadi perhatian kusus bidang kesehatan. Salah satunya di Provinsi Bali. Penyebab terbanyak mortalitas ibu di Provinsi Bali dikarenakan oleh faktor obstetri dan non obstetric. Kejadian rata-rata kasus non obstetri kisaran 50% setiap tahunnya. Berdasarkan kasus non obstertri tersebut dapat memperlihatkan penanganan persalinan ibu yang belum mencapai optimal. Di Provinsi Bali, masih mengalami kesulitan untuk menurunkan kasus AKI secara signifikan. Berdasarkan hal tersebut menunjukkan bahwa kendala yang dihadapi
masih sangat komplek. Kendala tersebut antara lain: 1) Fasilitas dan kualitas pelayanan kehamilan belum optimal; 2) Persebaran tenaga kerja yang belum merata; 3) Mutu pelayanan, sistem dan sumber daya tidak optimal. Dengan adanya hal tersebut, perlu adanya penelitian faktor-faktor yang memberikan pengaruh signifikan terhadap angka kematian ibu sebagai rekomendasi kepada pemerintah untuk mengurangi AKI di Provinsi Bali. Salah satu upaya yang dapat dilakukan untuk mengurangi AKI yakni mengidenfikasi faktor-faktor apa saja yang mempengaruhi terjadinya kasus AKI menggunakan analisis regresi. Setelah dilakukan analisis maka dapat dilakukan tindakan penekanan faktor yang menyebabkan kematian ibu.
Kasus AKI merupakan data cacah yang menyatakan banyaknya kejadian kematian ibu dalam interval waktu tertentu. Salah satu analisis regresi yang dapat digunakan untuk menganalisis hubungan antara variabel respon yang berupa data cacah dengan satu atau lebih variabel prediktor yakni model regresi Poisson. Model Poisson biasanya difungsikan dalam memodelkan data hasil pencacahan data yang
terkandung peluang kecil dengan kejadiannya dan dapat disesuaikan pada waktu atau daerah tertentu (Febriani et al., 2015).
Pemodelan menggunakan regresi Poisson harus memenuhi asumsi nilai mean dan variansinya sama (equidispersi). Namun dalam analisis data cacah dengan menggunakan model regresi Poisson terkadang terjadi pelanggaran asumsi tersebut, dimana nilai variansinya lebih besar dari nilai mean yang disebut overdispersi atau kondisi varian lebih kecil dari nilai mean yang disebut underdispersi (Cahyandari, 2014). Pemodelan regresi Poisson dengan data yang mengandung overdispersi menyebabkan galat baku menjadi terlalu rendah (underestimate), sehingga pengambilan keputusan terhadap signifikansi parameter regresinya menjadi tidak tepat (Molla dan Muniswamy, 2012). Sehingga, perlu dilakukan pengujian overdispersi untuk memenuhi syarat analisis regresi Poisson.
Berdasarkan latar belakang tersebut dalam penelitian ini dilakukan pemodelan Angka Kematian Ibu (AKI) menggunakan metode analisis regresi Poisson dengan 6 faktor yang didugamenjadi penyebab kasus AKI sebagai berikut :
-
1. Persentase kunjungan ibu hamil K1,
-
2. Persentase kunjungan ibu hamil K4,
-
3. Persentase komplikasi kebidanan yang ditangani,
-
4. Persentase persalinan ditolong dengan tenaga Kesehatan,
-
5. Persentase ibu hamil imunisasi Td5,
-
6. Persentase ibu hamil imunisasi Td2+.
Model regresi Poisson dapat ditulis sebagai berikut:
yι = f(x∂ +εl ;i = 1,2,3,...,n (1)
dimana yi adalah jumlah kejadian dan μi adalah mean jumlah kejadian dimana μt diasumsikan tidak berubah dari data ke data.
Regresi Poisson menggunakan Generelized Linier Model (GLM), terdapat sebuah fungsi g yang linier yang menghubungkan mean dari variabel respon dengan variabel prediktor, yaitu:
g(μi) = m = βo + βιxn + - + βkxtk (2) fungsi g tersebut merupakan fungsi penghubung. Sedangkan hubungan antara mean dan prediktor linier adalah sebagai berikut:
K = g~1(m) = g~1(×tβ) (3)
Model regresi Poisson, biasanya fungsi penghubung yang digunakan adalah fungsi penghubung log, karena mean dari variabel
responnya akan berbentuk fungsi eksponenial dan menjamin bahwa nilai variabel yang ditaksir dari variabel responnya akan bernilai non-negatif. Fungsi penghubung log yaitu sebagai berikut:
9(μ∂ = In μl = xτiβ
Hubungan antara mean variabel respon dan prediktor linier dengan menggunakan fungsi log adalah:
In μi = xτβ
Kedua ruas diambil fungsi eksponensialnya, didapat:
elnμl = exτlβ
μi = extβ
Sehingga fungsi penghubung untuk model regresi Poisson seperti dituliskan pada persamaan di bawah ini:
In μi = xτiβ = βo+ β1xil + β2xi2 + -
+ βkxik
μi = exp(xτβ) = exp(βo + β1Xi1 + β2xi2
+-----+ βkxik)
Selanjutnya penaksiran parameter model regresi Poisson dilakukan dengan menggunakan metode Maximum Likelihood Estimation (MLE).
Penggunaan R-Square (R2) dapat menggambarkan keeratan hubungan regresi antara peubah respon Y dengan peubah penjelas X. Nilai R2 yang semakin besar 0 ≤ R2 ≤ 1) menunjukan semakin tepat dugaan dari model regresi. Ada beberapa ukuran R2 yang telah dikembangkan dalam model regresi Poisson (Heinzl dan Mittlböck, 2003). Penggunaan ukuran R2 yang didasarkan pada sisaan deviance (deviance residual) sebagai berikut:
n 2 _ 1 _ lnL(y)-lnL(μ)
Dev lnL(y)-lnL(y)
(4)
dimana In L (y') adalah log likelihood ketika semua parameter βj (j = 0,1, ...,k') tidak disertakan dalam model dan yl adalah nilai pengamatan peubah respon ke-i. lnL(μ) adalah log likelihood ketika semua parameter βj disertakan dalam model dan μl nilai cocokan (predicted value) untuk obsevabel ke- i. In L(y) adalah log likelihood ketika hanya β0 yang disertakan dalam model dan y adalah rata- rata respon.
Pengujian hipotesis parameter regresi Poisson terdiri dari pengujian hipotesis parameter model regresi Poisson secara serentak
dan parsial. Hipotesis pengujian parameter model regresi Poisson secara serentak adalah: Ho^β1=β2=...= βp = 0
H1: paling sedikit ada satu βk≠0;^ = 1,2, ...,p Statistik uji pengujian hipotesis parameter regresi Poisson ditentukan berdasarkan metode Likelihood Ratio Test (LRT). Pengujian hipotesis parameter model regresi Poisson selanjutnya adalah pengujian hipotesis secara parsial dengan hipotesis:
H0:βk = 0
H1:βfc ≠ 0
Statistik uji yang digunakan adalah statistik Wald dengan perhitungan berikut:
7 — ⅞
Z = *e(‰)
dimana statistik Z berdistribusi normal baku. Daerah penolakan H0 adalah menolak H0 pada taraf uji a jika nilai dari |Z| > Za∕2.
Jenis data pada halaman berikut ini adalah kuantitatif nonparametrik. Observasi pengujian didasarkan pada data sekunder yang diterima pada tahun 2018 dari Dinas Kesehatan Provinsi Bali. Data tersebut berupa mortalitas ibu di 57 kecamatan di Provinsi Bali pada tahun 2018.
Terdapat dua jenis variabel pada penelitian ini yaitu angka mortalitas Ibu se-Kecamatan di Provinsi Bali sebagai variabel respon (Y) dan 6 variabel prediktor (X) sebagai berikut Persentase kunjungan ibu hamil K1 (X1),
Persentase kunjungan ibu hamil K4 (X2),
Persentase komplikasi kebidanan yang ditangani (X3), Persentase persalinan ditolong dengan tenaga Kesehatan (X4), Persentase ibu hamil imunisasi Td5 (X5), Persentase ibu hamil imunisasi Td2+ (X6).
Analisis data terdapat runtutan tahap yaitu:
-
1. Menyajikan statistika deskriptif umum untuk mendapatkan gambaran data tentang kasus AKI di Provinsi Bali.
-
2. Melakukan pengujian distribusi Poisson data peubah respon (AKI)
-
3. Pengujian overdispersi pada data peubah respon (AKI)
-
4. Pengujian Multikolinearitas antar variabel predictor
-
5. Memodelkan AKI (variabel respon) dengan variabel prediktor yang telah ditetapkan dengan menggunakan regresi Poisson
-
6. Menghitung nilai R Square (R2)
-
7. Menginterpretasikan model hasil analisis yang diperoleh dari metode regresi Poisson dan menarik kesimpulan.
Data sekunder diperoleh dari Dinas Kesehatan Provinsi Bali pada tahun 2018 kemudian dilakukan pengolahan statistika diskriptif untuk mendapatkan gambaran umum data yang tersedia dan merupakan gabungan dari seluruh kecamatan yang ada di Bali. Gambar 1 menunjukkan kasus AKI tahun 2018 tertinggi terjadi di 4 kecamatan yakni Kintamani,
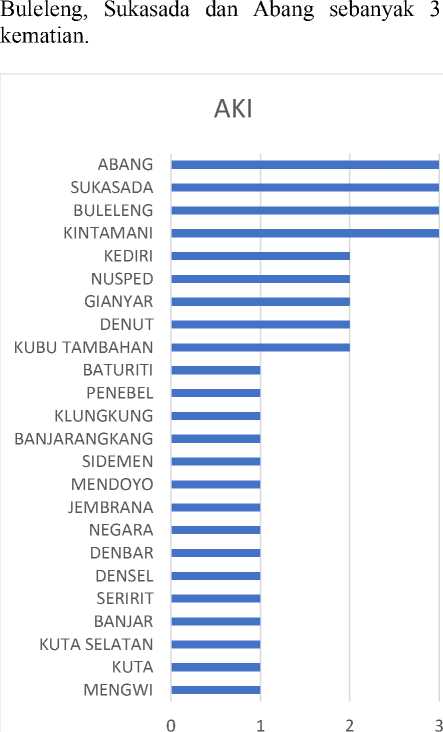
Gambar 1. Grafik Angka Kematian Ibu per Kecamatan di Provinsi Bali Tahun 2018
Dapat dilihat pula gambaran rerata, nilai minimum dan maksimum data dari masing-masing variabel pada penelitian ini yang disajikan pada Tabel 1 menunjukkan kasus AKI
terbesar dengan sebanyak 3 kasus sedangkan terendah adalah 0 kasus (33 kecamatan). Rata-rata persentase kunjungan ibu hamil K1 (X1) yakni 18.65% dengan prsentase maksimum yaitu 98.09% dan minimum yaitu 2.93%. Pemeriksaan kesehatan ibu hamil harus mencapai jumlah minimum pada setiap kehamilan. Jumlah minimum tersebut dilakukan pada Trimester I paling rendah 1 kali dalam mengunjungi dokter (Setidaknya sekali selama trimester pertama (usia kehamilan 0-12 minggu), setidaknya dua kali selama trimester kedua (usia kehamilan 12-24 minggu), dan setidaknya dua kali selama trimester ketiga (usia kehamilan 24 minggu sampai lahir). Setiap pemeriksaan yang dilakukan disarankan untuk menggunakan standar pelayanan agar ibu hamil atau janin mendapatkan perlindungan dini dari komplikasi serta deteksi dini faktor risiko kehamilan. Kunjungan ibu hamil K1 adalah kunjungan pertama ibu hamil yang telah menjalani pemeriksaan kehamilan. Pada kunjungan pertama akan dilakukan pemeriksaan riwayat kehamilan, penyakit kehamilan saat ini, riwayat penyakit keluarga, dan pemeriksaan umum.
Pada data kunjungan ibu hamil K4 merupakan kunjungan ibu hamil yang sudah memperoleh pelayanan sesuai dengan jadwal dan telah dianjurkan pada tiap trimesternya. Rata-rata persentase kunjungan ibu hamil K4 ( X2) 15.69%. Presentase terbesar ibu hamil K4 yang datang memeriksakan kandungannya sebanyak 45,79% dari total keseluruhan jumlah yang hamil. Sedangkan terendahkan yaitu 2.93% dari kejadian yang terjadi
Sedangkan untuk faktor ketiga yaitu tingkat komplikasi kebidanan yang ditangani tertinggi yaitu 46.71% artinya adanya kejadian komplikasi kebidanan di Bali yang mencapai 46,71% dari keseluhan komplikasi yang terjadi. Tingkat terendah yaitu pada sebesar 2.02% yang mengartikan bahwa kejadian komplikasi kebidanan yang ditangani di Bali terendah hanya hingga 2.02%. Komplikasi kebidanan merupakan ibu yang mengalami komplikasi di daerah dan periode waktu tertentu dan dikelola pada tingkat dasar dan sesuai dengan kriteria yang ditetapkan oleh penyedia layanan kesehatan yang berkualitas. Ketika melayani, terutama bidan di pedesaan dan puskesmas sebagaian ibu hamil berisiko tinggi atau mengalami komplikasi sehingga dierlukan pelayanan kesehatan. Karena keterbatasan kapasitas untuk memberi pelayanan dilakukan cara untuk merujuknya ke pelayanan kesehatan
yang sesuai. Sedangkan proses bersalinan dengan tenaga kesehatan adalah pelayanan yang diberikan oleh tenaga kesehatan dengan kemampuan kebidanan.
Tabel 1. Nilai Mean, Maksimum dan Minimum Variabel Penelitian
|
Variabel |
Mean |
Minimum |
Maksimum |
|
Y |
0,64 |
0,00 |
3,00 |
|
X1 |
18,65 |
2,93 |
98,09 |
|
X2 |
15,69 |
2,93 |
45,79 |
|
X3 |
15,38 |
2,02 |
46,71 |
|
X4 |
15,70 |
3,28 |
47,69 |
|
X5 |
14,01 |
0,00 |
41,78 |
|
X6 |
14,05 |
0,00 |
38,60 |
Sumber : Data diolah (2021)
Proses bersalin dengan bantuan tenaga kesehatan mampu menjamin kualitas pelayanan pencegahan infeksi dan metode pertolonganpun sesuai dengan standar pelayanan. Pemerintah pusat mengeluarkan kebijakan Jaminan Persalinan (Jampersal) untuk memperluas daerah pertolongan bersalin yang diberikan. Kebijakan jaminan persalinan bertujuan untuk memudahkan sisi ekonomi ibu hamil. Adanya hal tersebut agar diperoleh keselamatan bersalin, termasuk pemeriksaan kehamilan, pelayanan pasca persalinan termasuk KB, dan pelayanan bayi baru lahir. Oleh karena itu pelayanan persalinan yang ditolong oleh tenaga kesehatan harus terlaksana dengan baik dan memenuhi standar. Berdasarkan hasil data menunjukkan kasus kematian ibu pada tingkat persalinan yang ditangani tenaga kesehatan tertinggi yaitu 47.69% dan terendah yaitu 3.28%. Berdasarkan hasil tersebut dapat dinyatakan terdapat ketimpangan kasus kematian ibu yang disebabkan kurangnya bantuan tenaga kerja yang belum merata.
Tetanus adalah suatu penyakit menular yang menyebabkan tingginya mortalitas pada bayi. Pengendalikan infeksi tetanus yaitu dilaksanakannya vaksinasi Tetanus Toksoid (Td) untuk wanita usia subur dan ibu hamil. Pada tahun 2017, Menteri Kesehatan mengeluarkan Peraturan Menteri No. 12 tentang Imunisasi, yang mengatur bahwa wanita usia subur dan ibu hamil termasuk dalam kategori yang perlu divaksinasi lebih lanjut. Berdasarkan data dari Dinas Kesehatan Provinsi Bali tahun 2018 persentase ibu hamil imunisasi Td5 tertinggi terjadi di Kecamatan Kintamani sebesar 41.78% sedangkan persentase ibu hamil imunisasi Td5 dengan persentase terendah sebesar 0%. Sedangkan Imunitas Td2+ adalah cakupan total ibu hamil
yang mendapat imunitas tetanus dan difteri (Td) lengkap dari Td1 sampai Td5.. Ditemukan persentase ibu hamil imunisasi Td2+ tertinggi sebesar 38.6% pada Kecamatan Kintamani sedangkan kecamatan dengan persentase ibu hamil imunisasi Td2+ terendah dengan persentase 0% .
Sebelum melakukan analisis, dilakukan uji kecocokan distribusi pada data AKI yang terjadi di Provinsi Bali dengan hipotesis berikut:
H0: data AKI di Provinsi Bali mengikuti distribusi Poisson
H1: data AKI di Provinsi Bali tidak mengikuti distribusi Poisson
Hasil uji khi-kuadrat pada kecocokan distribusi Poisson pada data peubah respon (AKI) diperoleh nilai χ2 (1.47) < ∕2.05,6 (12.59) dengan p_value sebesar 0,224. Sehingga, keputusan hasil uji chi-square adalah gagal tolak H0 yang menunjukkan AKI di Provinsi Bali berdistribusi Poisson.
Selanjutnya dilakukan pengujian
overdispersi peubah respon (AKI) dengan uji khi-kuadrat. Hipotesis yang ditentukan : H0: tidak terdapat overdispersi pada data H1: terdapat overdispersi pada data
Hasil uji overdispersi menunjukkan signifikansi lebih dari 0,05 sehingga dapat disimpulkan tidak terdapat overdispersi dari data AKI di Provinsi Bali. Oleh karena itu analisis Regresi Poisson dapat digunakan pada penelitian ini.
Pengujian multikolinearitas dapat ditentukan dengan nilai Variance Inflation Factor (VIF). Data yang tidak mengalami gejala multikolinearitas ketika memiliki nilai VIF kurang dari 10. Apabila sebuah peubah atau X memilikinilai VIF lebih dari 10 maka dapat dilakukan pereduksian. Pereduksian Analisis komponen utama melalui VIF ini pada dasarnya bertujuan untuk menyederhanakan peubah yang diamati dengan cara menyusutkan (mereduksi) dimensinya (Widiharih, 2001).
Tabel 2. Nilai VIF Variabel Bebas
|
X1 |
X2 |
X3 |
X4 |
Xs |
X6 |
|
1.08 |
107.73 |
5.24 |
111.06 |
18.40 |
18.19 |
Hasil pengujian multikolinearitas Tabel 2 menunjukkan bahwa variabel X2, X4, X5, dan X6 memiliki nilai VIF lebih dari 10. Hal ini menunjukkan terdapat korelasi antara variabel bebas sehingga diperlukan penanganan
multikolinearitas. Oleh karena itu dilakukan eliminasi variabel X2 , X4, X5, dan X6 yang memiliki nilai VIF lebih dari 10. Kemudian terpilih dua variabel bebas yaitu X1 dan X3. Karena data diperoleh nilai VIF variabel X1 dan X3 kurang dari 10.
Pemodelan dengan regresi Poisson digunakan untuk memodelkan AKI di Provinsi Bali (Y) dengan variabel penjelas yang sudah diseleksi yakni persentase kunjungan ibu hamil K1 (X1), presentase komplikasi kebidanan yang ditangani (X3). Melalui software R diperoleh pendugaan parameter model regresi Poisson disajikan pada Tabel 3 menunjukkan hasil pendugaan parameter dari model regresi Poisson dengan nilai AIC sebesar 113,97. Pengujian secara serentak dengan uji likelihood ratio test diperoleh statistik uji D(β) (21.274) > x2(0.05,6) (12,59) dengan p-value lebih kecil dari 0,05 yang berarti paling bahwa faktor X1 dan X3 berpengaruh nyata pada model. Dilanjutkan uji untuk menentukan dampak dari masing-masing variabel penjelas ini, hipotesis berikut digunakan untuk pengujian parameter:
H0: βi=1,3 = 0 (tidak ada variabel yang signifikan berpengaruh)
H1: βi=1,3 ≠ 0
Tabel 3. Nilai Dugaan Parameter Regresi Poisson
|
Parameter |
Nilai dugaan |
Galat Baku |
Nilai Z |
p_value |
|
£0 |
-1.763 |
0.3764 |
-4.68 |
0.0000 |
|
β1 |
0.0212 |
0.0065 |
3.252 |
0.0011 |
|
£3 |
0.0528 |
0.0211 |
2.503 |
0.0123 |
Hasil pengujian parameter secara parsial model regresi Poisson disajikan Tabel 3 dengan taraf signifikansi 5% menunjukkan terdapat dua faktor yang signifikan pada model yakni Persentase kunjungan ibu hamil K1 (X1) dan Persentase komplikasi kebidanan yang ditangani (X3). Persamaan model regresi Poisson dapat dituliskan sebagai berikut:
ln(μ) = -1.7632 + 0.0212X1 + 0.0528X3
Semakin ibu mengunjungi untuk pengecekan kehamilan maka semakin kecil resiko yang akan terjadi untuk kesehatan ibu dan bayinya. Tercapainya hal tersebut berasal dari pengalaman dan kesiapan jiwanya (Nursalam, 2008), pada usia cukup dapat menjadikan seorang ibu berfikir dewasa dalam memenuhi kesehatannya, contohnya saja adalah pemeriksakan rutin kehamilan sejak dini. Komplikasi persalinan merupakan peristiwa
yang menjadikan jiwa terasa terancam baik dari sisi ibu atau janin yang disebabkan dari persalinan itu sendiri (Basu et al., 2014).
Model regresi Poisson memiliki nilai R-squared yang kecil yakni 0,1671. Temuan ini menunjukkan bahwa variabel penjelas dalam penelitian hanya dapat menjelaskan 16,17% varians dalam variabel respon, artinya terdapat pengaruh dari kedua faktor (X1 dan X3) sebesar 16,71%. Hal ini menunjukkan bahwa diduga masih banyak faktor lain yang mempengaruhi kasus AKI namun belum diikutkan dalam variabel penelitian ini.
Hasil penelitian analisis regresi Poisson kasus AKI di Provinsi Bali menunjukkan variabel Persentase kunjungan ibu hamil K1 (X1) dan Persentase komplikasi kebidanan yang ditangani (X3) berpengaruh signifikan terhadap kasus AKI dengan model Regresi Poisson yang terbentuk adalah: ln(μ̂) = -1.7632 +
0.0212X1 + 0.0528X3.
Nilai R-squared cukup rendah yakni 16,71%, sehingga pengaruh sisanya yaitu 83, 29%
menunjukkan bahwa terdapat variabel lain di luar model memengaruhi kasus AKI, diharapkan penelitian selanjutnya dapat menambah variabel lain. Selain itu, kejadian AKI cenderung mempunyai banyak data bernilai 0, selanjutnya dapat menggunakan alternatif Zero Inflated Poisson Regression untuk kasus Poisson dengan nilai 0 yang cukup banyak.
DAFTAR PUSTAKA
Basu, et al. 2014. Knowledge, Attitude And Practices Of Women In Maldives Related To The Risk Factors, Prevention and Early Detection Of Cervical Cancer. (diakses pada tanggal 23 Maret 2017 melalui http://dx.doi.org/10.7314/APJCP.2014.15.1 6.6691
Cahyandari, Rini. 2014. Pengujian Overdispersi pada Model Regresi Poisson (Studi Kasus Laka Lantas Mobil Penumpang di Provinsi Jawa Barat). Jurnal Matematika, UIN Sunan Gunung Jati. Vol.14 No.2, 69-76
Cameron AC, Trivedi PK. 2013. Regression Analysis of Count Data. Cambridge (UK): Cambridge University Press.
Darnah. 2011. Mengatasi Overdispersi pada Model Regresi Poisson dengan Generalized Poisson Regeresion I. Jurnal Eksponensial.
Febriani, et al. 2015. Analisis Regresi Poisson untuk Mengetahui Variabel yang
Berpengaruh pada Kasus Gizi Buruk di Kabupaten Bangka. Jurnal Matematika dan Pendidikan Matematika UNY. Yogyakarta.
Hardin JW, Hilbe JM. 2007. Generalized Linier Models and Extensions. Texas : Stata Press.
Heinzl H, Mittlböck M. 2003. Pseudo R-squared Measures for Poisson Regression Models with Over- or Underdispersion.
Computational & Data Analysis 44 (2003). 253-271.
Molla DT, Muniswamy B. 2012. Power of Tests for Overdispersion Parameter in Negative Binomial Regression Model. Journals of Mathematics. 4(1): 29-36.
Novarani Putri S, D. A. 2016. Pemodelan Faktor- Faktor yang Memengaruhi Kematian Ibu di Kota Surabaya Berdasarkan Antenatal Care Menggunakan Regresi Binomial Negatif. Jurnal Sains dan Seni ITS, Volume 5, Nomor 2.
Nursalam. 2008. Konsep dan Penerapan Metodologi Penelitian Ilmu Keperawatan. Jakarta: Salemba Medika.
WHO, UNICEF. (2000). Maternal Mortality in 2000. World Health Organization (WHO)/ The United Nation Children"s (UNICEF).
Widiharih, Tatik. 2001. Penanganan Multikolinearitas (Kekolinearan Ganda) Dengan Analisis Regresi Komponen Utama. Jurnal Matematika dan Komputer, Volume 4, Nomor 2.
11
Discussion and feedback