TEOREMA RESIDU DAN APLIKASINYA DALAM INTEGRAL TAK WAJAR

E-Jurnal Matematika Vol. 11(1), Januari 2022, pp. 1-5

DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p352

ISSN: 2303-1751

TEOREMA RESIDU DAN APLIKASINYA DALAM INTEGRAL TAK WAJAR

Moh. Atkurrahman^1§, Muniar Zulfitni², Diyah Ayu Rizki Pradita³

¹Ibrahimy University, Situbondo, Indonesia [Email: [email protected]] ²IPB University, Bogor, Indonesia [Email: [email protected]]

³Ibrahimy University, Situbondo, Indonesia [Email: [email protected]] ^§Corresponding Author

ABSTRACT

In this study discusses about the solve of improper integral uses ordinary step and the solve uses residu theorem. For the ordinary step is used the concept of integral and substitution integral, and the for the residu theorem is used the concept of a series from complex functions in complex areas. this study purpose for apply the residue theorem to improper integral of the real function. And know the proportion to calculate the integral value using the residue theorem and the ordinary steps, and applying the residu theorem in calculating improper integral of the real function that can't be done using the ordinary steps. Using concepts or approaches of complex function series thus produced the formula to calculate the improper integral of the real function. And the result of this study is that calculating unnatural integrals is easier and faster using the residue theorem than using the ordinary step. Not all the integral to the real function can be calculated using the ordinary steps therefore it can be used the residu theorem formula as an alternative.

Keywords: integral tak wajar, teorema residu, fungsi kompleks, deret

persoalan atau permasalahan tersebut (Ward Brown & Churchill, 2009).

Dalam kalkulus, integral tak wajar merupakan salah satu bentuk integral yang dapat didefinisikan dengan persamaan berikut

r ∞             f R

I   f(x)dx = I  f(x)dx.

' 0                         -'o

Persamaan tersebut berlaku pada fungsi f(x)

yang continue dan x ≥ 0, sedangkan pada fungsi f(x) yang continue dan x < 0 didefinisikan atau dinyatakan dengan persamaan berikut

00 I f(x)dx = I J-∞           Rr

f(x)dx.

Dengan kata lain konsep integral tak wajar mencakup batas atas tak terhingga dan batas bawah negatif tak terhingga. Pada interval pengintegrasian ketika dalam interval a ≤ x ≤ b, ada yang menyebabkan f(x) discontinue. Hal ini berakibat fungsi tersebut tidak dapat diintegralkan pada titik f(x) discontinue. Titik yang membuat f(x) discontinue disebut titik

singular.

Teorema residu merupakan suatu cara untuk menghitung nilai integral pada fungsi yang memiliki satu atau lebih titik singular. Teorema residu sering digunakan dalam penyelesaian integral fungsi kompleks, akan tetapi teorema residu juga dapat diterapkan pada integral fungsi bernilai real. Oleh karena itu penulis ingin mengaplikasikan konsep teorema residu pada integral tak wajar menggunakan fungsi real.

Pengertian Integral Tak Wajar adalah limit dari integral tentu dengan batas pengintegralan mendekati bilangan real tertentu atau ∞, -∞ atau pada beberapa kasus yang mencakup keduanya. Dengan kata lain, integral tak wajar adalah limit dalam bentuk:

f b                 rb

I f(x)dx = I

J-∞           Ja

n ∞              b^

I f(x)dx = I

J a               a_a

f(x)dx,

f(x)dx,

atau dalam bentuk kedua limit tak terhingga

r ∞              qO              b b

I   f(x)dx = I f(x)dx + I f(x)dx

j-∞           a_a            Jq

Jika limit-limit pada ruas kanan ada dan mempunyai nilai-nilai terhingga, maka dapat

dikatakan bahwa integral tak wajar konvergen. Jika tidak maka integral tersebut divergen (Galán-García et al., 2018).

3. HASIL DAN PEMBAHASAN

Dalam pembahasan kali ini akan di berikan sebuah metode atau teorema yang dapat membantu dalam menyelesaikan permasalahan integral tak wajar pada fungsi real, tetapi diberikan terlebih dahulu Teorema Residu. Konsep dasar Teorema Residu diperoleh dari konsep deret.

Teorema 3.1 (Ward Brown & Churchill, 2009) Misalkan C kontur tertutup sederhana berorientasi positif yang terdiri dari titik interior dan perbatasan kontur C yang membuat fungsi f analitik kecuali pada bilangan berhingga dari titik singular z₁,z₂, ...,z_m titik interior C. Jika b₁,b₂,-,b_m dinotasikan sebagai residu dari masing-masing titik, maka : m

{           n      ^Res f(z)

I ^f(^z)^dz = 2_m∑ ^c                 k=1

Bukti :

Misalkan titik singular z_k (k = 1,2, ..,m') adalah pusat dari kontur tertutup sederhana berorientasi positif C_k yang berada pada interior kontur tertutup sederhana C, maka terdapat r_k > 0 (j = 1,2, ...,m), sedemikian hingga f(z) analitik pada setiap anggota N_r.(z_k^). Dengan menggunakan perluasan Teorema Cauchy Goursat pada daerah terhubung berganda maka berlaku:

f     ^)

Titik z₁ merupakan salah satu titik singular yang terdapat pada kontur C_k, sehingga menggunakan penjabaran dari definisi deret laurent, berlaku: ∞∞

f⁽z) = ∑ a_n(z- z₀)ⁿ + ∑ b_n(z- z₀) ⁿ,

n=0              n=1

untuk setiap z ∈ N_r-_ι(z₁), dimana f(z) ^an   2πi)_c (z-z₀yⁿ+^1dz

b_n ^i r  ^f(z)n I^dz

2πij_c (z-z₀)^{n 1}

Penjabaran untuk a_n dan b_n

a₀=^( -^f(^z)-dz 2πi C_c z — z₀

Jjz_, ^a1   2πiic (z-z₀)2^dz

_n - Xf f(z)

²   2πiJ_c (z-z₀)³

-Kz, ^a3   2πiic (z-z₀)4^dz

^an 2πi^fc (z — zo)ⁿ⁺¹

^bι L^{f fz})^dz

Dari gambar diperoleh:

R

f S. ∖ dx + f f(z)dz = 2πi

J Q(X) J

-R

^cR

n

ΣRes f(z)

z → z_k

k=1

^b2

=If

2πi J_c

f (z) „

-----dz

z —zo

b

=^f

2πiJ_c (z

fto

—

^bn   2πi^f_c (z

Zo)² fto

dz

R

f ^p(x) J

I 7^dx = —

J Qto

-R

n

f f(z)dz + 2πi ∑

^cR

.

k=i

R

Res f(z} ^z→^zk

— zo)^n-1

dz

f                 f Pto

Ketikajim f f(z)dz = 0, maka f Q~^dx

^cR

-R

Dari barisan a_n dan b_n terlihat bahwa pada saat n = 1 pada bagian b_n diperoleh:

b1 = ^ii f(z~)dz.

Maka residu dari fungsi tersebut yaitu

2πib₁ = f f(z~)dz, ' c

1

dimana b₁ merupakan koefisien residu dari ^;^-.

Berdasarkan hal tersebut maka perluasan dari Cauchy Goursat adalah

f f (z') dz = 2πib₁ + 2πib₂ + 2πib3 +

+ 2πib_n

n

n

= 2π_iy^^s f'

Z-L z→zk k=1

Akan di berikan beberapa contoh mencari integral menggunakan cara biasa dan residu.

Contoh 1 :

Hitunglah nilai limit dari

C ∞    1

L x²+1^dx

Dengan menggunakan cara biasa

f f(z)dz = 2πi∑

Res f(z) ^z→^zk

(pembuktian Teorema selesai).

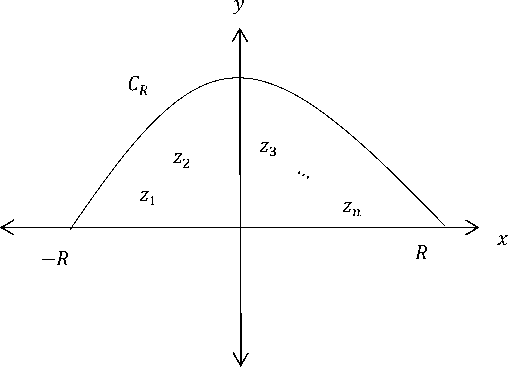
Teorema Residu tersebut diperoleh menggunakan pendekatan fungsi kompleks pada bidang kompleks. Nilai integral pada fungsi real dapat didekati menggunakan pendekatan fungsi kompleks perhatikan gambar berikut :

r ∞               r R

L x²+1^dx =J-R

Misal : x = tan tan θ dx = θ dθ. sehingga,

C ^r 1          Γ^r

L_r x²+1^dx = ⁱ

=J^r

J-R

1

—v dx x² + 1

1

---7—7 (θ dθ) tanθ + 1

1

g- (θ) dθ

IT

=J^r

J-R

θ

θ + θ ^dθ θ

= I^{r θ} d

J-R —

=J^r

^j-R

θ sec²θ —^dθ

= lim(θ | R)

R→∞   -^r'

= lim (arc tan x | ^r) R→∞           ^R

= lim (arc tan R — cos

R→∞

Gambar 3.1. Representatif Geometri Integral Tak Wajar Menggunakan Residu

tan (—R)) = (arc tan ∞

_—

arc tan (—∞))

= - + - = π. 2    2

Dengan menggunakan konsep teorema residu

(∞    1          f^β 1

∫_-∞ ^²+ι^dx = L_r ^^ι^dx

f^R 1        1    4

= J-R (7+1) LX-V^dx

Untuk titik singular x₀ = i., maka, f(^χo') = 7+i = τk = τ_i, ^sehingga

Γ ^r 1

lim    ——— dx = 2πi .

R→∞ -..r (x² + 1)

f(x₀) = 2πi.

1 = π.

2i

Contoh 2 :

Hitunglah nilai integral dari r 0     3

J-∞ X³ + x

C⁰       1

^j_-r tan tan θ

Γ⁰ COSCOS θ

= ³J-r sn^ ^dθ∙

Misal : sin θ = u cos θ = du .

Sehingga, f ^r cos cos θ

3 lim I ------;---- dθ

R→∞J_-r SinSin θ

= 3∫ ¹ du

J-r ^u

= 3(∣n u)]_-^r_r

R

= 3∣n(sin(arc tan tan x))] __R

= 3(∣n(sin(arc tan tan RJ) — ∣n(sin(arc tan tan (-R))))

= (∣n(sin(arc tan tan (∞))) — ∣n(sin(arc tan tan (-∞))))

= 3 (|n (sin sin (-) ) — |n (sin sin (—-) )

= 3 (|n (1) +sin sin (1) )

= 3 (0 + 0) = 0 .

Dengan cara biasa

(⁰     3           f⁰       3

J-∞ x³ +x^dx   L₀₀ x(x² + 1)^xX

0₃ lim    -t-t—77 dx

R→∞ --_r x(x² + 1)

0₁ lim 3   ———— dx.

R→∞ --_r x(x² + 1)

Dengan Teorema residu ^∞3          ^∞

L x^3r+x^dx=³L∞

= L

J-r ■

1

——5—dx , x(x² + 1)

1

-t-t—TT dx x(x² + 1)

Misal : x =tan tan θ, maka dx = θ dθ, sehingga

1

--TT dx x(x² + 1)

lim 3 J

λ→∞  -_rR

r ^r 1      1

= ³L_r x. (x² + 1J^dx

Jik x² + 1 di ambil sebagai titik singular maka, 1

f(xj = x sehingga diperoleh 2 titik singular

Yaitu x₀  = —

f(x₀) = A

= 3f

^j-r

• -    i atau X₀ = i jadi

1

• -    = i atau f(x₀) = t

-i

1

-----;----.           . ^ θ dθ

tan tan θ ((tanθ)² + 1)

_   f⁰

J-R_r t     (tanθ  ₁∖²^^

tan tan θ (-^--+1)

{⁰

= Jr       θ +θ ^dθ

• ^-r tan tan θ(——

• (⁰θ

• = 3 I — dθ

• ^j-r tan tan θ (&)

• f⁰ θ

• = 3 I

• j_-r tan tan θθ

f ^r 1      1

sehingga,    ₃J_-r x . _ιx,_llι^dx

= 2πi (i + (-i)) = 2πi (i — i') = 2πi (0) = 0.

Contoh : 3

teorema residu dalam menghitung integral tak wajar yang tidak bisa diselesaikan dengan cara biasa

1”

J-R

1

%² + 1

dx

C ^r 1           1

J_-r (x + 1) ' (x² - x + 1) ^Xx

Misal : x₀ = f⁽x) =

f(×o^) =

—1 maka

1 x²-x+1 ’

1

(-R — (—1) + 1

11

1+1+1 3

^jadi L x + 1 = ^2πi ∑ ^R-^(x)

= 2πi¹ = ²πi.

3    3

4. KESIMPULAN DAN SARAN

Dari pembahasan di atas maka dapat disimpulkan bahwa aplikasi teorema residu pada integral tak wajar dirumuskan dalam bentuk:

^R z                              ⁿ

T ^p(x^    f         R.SfRes f(z)

I , dx + I f(z)dz = 2πi >

J Q(x)     J            Z→ z→ z_k

-R            Cr                ^k=¹

Ketika

lim f f(z)dz

R→∞ J ^cR

R

„     ,    ( P(x) ,

= 0, maka I —-- dx J Q⁽x)

-R n = 2πi∑^Resf(z) z→zk k=1

■

1.

2.

Perbandingan menghitung integral tak wajar menggunakan teorema residu dan cara biasa itu lebih mudah dan cepat menggunakan teorema.

Penerapan Teorema residu dalam menghitung integral tak wajar yang tidak bisa diselesaikan dengan cara biasa.

C ^r 1

^f_-R x²+l^dx

C^R 1           1

^f_-R (x + 1) ■ (x² - x + 1) ^xx

Misal : x₀ = —1 maka

^f(x) = ⅛ , ^f(xo) = (-R⅛5+1

'a^di ∫-_r x + 1   ^2πi Σ ^(x)

= 2πi¹ = ²πi.

33

Dalam artikel ini teorema residu hanya berlaku pada fungsi yang tidak analitik pada satu titik atau lebih dan fungsi dimana penyebutnya berderajat 1. Oleh karena itu penulis menyarankan untuk meneliti lebih lanjut pada fungsi yang berderajat lebih dari 1. Hasil: Nilai integral tak wajar sangat dipengaruhi terhadap pemilihan titik singular x₀ dan f(x₀ ) ketika xo =zo

DAFTAR PUSTAKA

Galán-García, J. L., Aguilera-Venegas, G.,

Galán-García, M., Rodríguez-Cielos, P., & Atencia-Mc.Killop, I. (2018). Improving CAS capabilities: New rules for computing improper integrals. Applied Mathematics and   Computation,   316,   525–540.

https://doi.org/10.1016/j.amc.2016.12.024

Toto. (2018). Aplikasi kalkulus dalam perkuliahan fisika. Prosiding Seminar Nasional Matematika dan Pendidikan Matematika (SNMPM), 2(1), 26–33.

Ward Brown, J., & Churchill. (2009). Complex Variables And Applications Complex Variables And Applications, Eighth Edition Library of Congress   Cataloging-in-

Publication                         Data.

https://math.unice.fr/~nivoche/pdf/Brown-Churchill-Complex    Variables    and

Application 8th edition.pdf

1        1

1+1+1=3

5