PENGGUNAAN MODEL ARIMAX UNTUK MERAMALKAN DATA CURAH HUJAN BULANAN DI BALI
on
E-Jurnal Matematika Vol. 10(4), November 2021, pp. 186-191
DOI: https://doi.org/10.24843/MTK.2021.v10.i04.p341
ISSN: 2303-1751
PENGGUNAAN MODEL ARIMAX UNTUK MERAMALKAN DATA CURAH HUJAN BULANAN DI BALI
Chairun Nisa1§, I Wayan Sumarjaya2§, I Gusti Ayu Made Srinadi3
1Program Studi Matematika, FMIPA Universitas Udayana [Email: chairun321@gmail.com]
2Program Studi Matematika, FMIPA Universitas Udayana [Email: sumarjaya@unud.ac.id]
3Program Studi Matematika, FMIPA Universitas Udayana [Email: srinadi@unud.ac.id]
§
Corresponding Author
ABSTRACT
Erratic raifall in the future has a major effect on life. Extreme rainfall can result in vaarious natural phenomena that have a negative impact in various fields work. The aim of this research is to find the best rainfall forecastng model in Bali using ARIMAX modeling, namely the transfer function model with an indeks Nino 3.4 as the input series. The transfer function model is a time series model that combines the regression approach and the ARIMA model for its error. Forecasting results suggest that the rainfall is linearly related to the Nino 3.4 indeks in the previous month. The best rainfall forecasting model has a value Akaike information criterion (AIC) is equal to 1334,629.
Keywords: ARIMAX, Transfer Function Model, Indeks Nino 3.4, Erratic Rainfall in Bali.
Peramalan atau forecasting adalah aktivitas memprediksikan sesuatu yang akan terjadi pada masa mendatang. Memprediksi sesuatu pada masa mendatang memerlukan data-data yang akurat pada masa lampau. Hasil peramalan yang baik diperoleh dengan melakukan analisis pada data untuk mendapatkan model yang tepat. Metode peramalan harus ditentukan dengan kehati-hatian dan ketelitian agar model yang diperoleh untuk melakukan peramalan adalah model yang tepat dan memiliki eror yang kecil, sehingga hasil peramalan yang diperoleh memiliki tingkat keakuratan yang baik.
Metode peramalan dengan menganalisis sekumpulan data pada masa lalu dalam periode waktu tertentu dengan jarak yang sama seperti data harian, bulanan dan seterusnya disebut metode peramala deret waktu. Data deret waktu tersebut akan digunakan untuk menentukan nilai pada masa mendatang.
Umumnya pemodelan autoregressive integrated moving average (ARIMA) paling sering diaplikasikan dalam peramalan. Pemodelan deret waktu ARIMA hanya memperhatikan satu variabel saja yaitu variabel yang menjadi fokus dan output peramalan tanpa memperhatikan variabel lain yaitu variabel eksogen yang dapat memengaruhi variabel yang
menjadi output peramalan. Oleh karena itu, diperlukan analisis deret waktu yang dapat memperhatikan variabel eksogen yang memengaruhi variabel yang menjadi output peramalan. Terdapat beberapa pemodelan deret waktu yang memiliki variabel eksogen seperti autoregressive distributed lag (ARDL), dan ARIMA with exogenous input (ARIMAX).
Pada dasarnya pemodelan ARIMAX menggunakan dua variabel sebagai indikator untuk menentukan nilai-nilai pada masa mendatang. Kedua variabel ini adalah variabel dependen dan variabel independen (Wangdi, dkk., 2010). Pada model ARIMAX terdapat tiga spesifikasi model berdasarkan pada konsep pendugaannya. Spesifikasi model ARIMAX antara lain model ARIMAX dengan estimasi simultan (simultaneous estimation), model ARIMAX dengan pendugaan model kovariatnya dahulu, dilanjutkan dengan pendugaan ARIMA untuk erornya (model fungsi transfer), dan model ARIMAX dengan pendugaan ARIMA untuk erornya, kemudian dilanjutkan dengan pendugaan model kovariatnya. Model fungsi transfer dapat diaplikasikan dalam meramalkan data curah hujan dengan melibatkan variabel eksogen yaitu indeks Nino 3.4.
Curah hujan merupakan banyaknya air hujan yang jatuh pada daerah dan periode waktu
tertentu (KBBI,edisi III). Letak astronomis Indonesia yang dilalui oleh garis khatulistiwa memengaruhi perubahan cuaca dan iklim serta tingginya tingkat curah hujan dan kelembapan udara yang menyebabkan pemanasan global dan efek rumah kaca. Bali berada pada 8° di selatan garis khatulistiwa yang menyebabkan suhu di Bali hangat yakni sekitar 26—27°C dan sekitar 85% tingkat kelembapan di Bali.
Curah hujan dipengaruhi oleh kelembapan udara, temperatur udara, kecepatan angin, aktivitas Madden Jullian Oscillation (MJO) atau masa udara basah, maupun fenomena alam lainnya seperti dinamika atmosfer El Nino Southern Oscillation (ENSO). Fenomena global dari sistem interaksi antara lautan dan atmosfer, ini yang dinamakan ENSO dengan dua kondisi yaitu El Nino dan La Nina. El Nino terjadi pada saat anomali suhu permukaan laut di Ekuator Pasifik Tengah positif, sedangkan La Nina terjadi saat anomali suhu negatif. Dampak yang disebabkan oleh ENSO ini dapat memengaruhi perubahan kondisi perairan Indonesia serta dapat mengakibatkan terjadinya pengurangan atau penambahan intensitas curah hujan. Mengingat wilayah Indonesia yang cukup luas maka ENSO hanya memengaruhi sebagian wilayah Indonesia. Pulau Bali merupakan salah satu wilayah di Indonesia yang dipengaruhi oleh kondisi ENSO.
Beberapa penelitian yang berhasil menerapkan model ARIMAX antara lain penelitian Dini dkk (2012) yang melakukan peramalan optimasi persediaan premium, dan penelitian Harahap dan Suharsono (2014) yang meramalkan jumlah sepeda motor yang terjual.
Penelitian ini bertujuan untuk menemukan model terbaik dalam meramalkan curah hujan bulanan di Bali. Metode peramalan deret waktu ARIMAX digunakan untuk meramalkan curah hujan di Bali dengan indeks Nino 3.4 sebagai variabel eksogen.
Penelitian ini menggunakan data curah hujan (yt) yang diamati oleh BMKG di wilayah Bali, dan data indeks Nino 3.4 (xt) yang diambil dari NOAA. Kedua data tersebut merupakan data bulanan yang tercatat pada Januari 2009 sampai Desember 2018.
Tahapan analisis pada penelitian ini menggunakan model ARIMAX berikut:
-
1. Mempersiapkan data curah hujan untuk deret input dan data indeks Nino 3.4 untuk
deret output;
-
2. Memeriksa kestasioneran deret input dan deret output dengan mengidentifikasi plot data deret waktu, plot ACF dan PACF.
-
3. Melakukan proses differencing atau transformasi pada data yang belum stasioner sehingga diperoleh data stasioner yang siap digunakan untuk tahap berikutnya;
-
4. Menetapkan model ARIMA terbaik untuk masing-masing deret;
-
5. Melakukan proses prewhitening dengan model ARIMA deret input terbaik yang diperoleh pada tahap sebelumnya untuk memperoleh nilai at (deret input setelah prewhitening) dan βt (deret output setelah prewhitening);
-
6. Menghitung nilai korelasi silang deret input dan deret output;
-
7. Menentukan nilai r, s, b berdasarkan plot korelasi silang;
-
8. Mengidentifikasi deret noise;
-
9. Menetapkan (pn, Qn) untuk model
ARIMA(pn, 0, Qn) dari deret noise;
-
10. Melakukan identifikasi akhir dan estimasi parameter model fungsi transfer;
-
11. Melakukan uji diagnostik model;
-
12. Melakukan peramalan curah hujan bulanan di Bali pada periode Januari 2020— Desember 2020.
-
3. HASIL DAN PEMBAHASAN
Identifikasi Data Deret Waktu
Tahapan pertama, identifikasi data pada masing-masing deret dengan membuat plot data deret input dan deret output pada Januari 2009 sampai Desember 2018. Hal ini dilakukan untuk mengetahui ada pola tren atau musiman pada data. Gambar 1 dan Gambar 2 adalah hasil plot data curah hujan sebagai deret output dan indeks Nino 3.4 sebagai deret input.
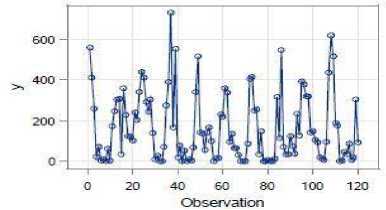
Gambar 1. Plot Data Asli Curah Hujan (Januari 2009—Desember 2018)
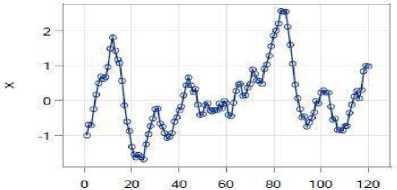
Observation
Gambar 2. Plot Data Asli Indeks Nino 3.4 (Januari 2009 - Desember 2018)
Pada Gambar 1 dan Gambar 2 menjelaskan bahwa data curah hujan dan indeks Nino 3.4 merupakan data non-stasioner dalam rataan. Gambar 1 menjelaskan bahwa terdapat pola musiman tahunan pada data, dengan data terendah bernilai nol. Gambar 2 menjelaskan bahwa data indeks Nino 3.4 mengalami fluktuatif dari waktu ke waktu, dengan data tertinggi berada pada data ke-80 dan terendah pada data ke-20 atau data ke-21 yang memiliki nilai kurang dari -1.

-
-1.0 -j ________ ________
0 5 10 15 20 25 30
Lag
Gambar 3. Plot ACF Data Asli Curah Hujan
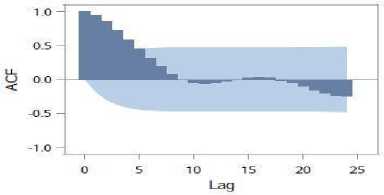
Gambar 4. Plot ACF Data Asli Indeks No 3.4
Pada Gambar 3 dan Gambar 4 terlihat bahwa plot ACF data curah hujan dan indeks Nino 3.4 mengalami dying down yang menunjukkan data non-stasioner. Oleh karena itu, dilakukan proses differencing terhadap tren dan musiman. Data curah hujan dan indeks Nino 3.4 yang telah stasioner dapat dibentuk model ARIMA deret input.
Penentuan Model ARIMA Deret Input
Orde untuk model ARIMA dapat diperoleh dengan mengidentifikasi nilai ACF dan PACF
deret input yang telah stasioner. Untuk menentukan orde AR dan MA non-seasonal maupun seasonal-nya dapat dilihat pada Gambar 5.

Gambar 5. Plot ACF dan PACF Data Indeks Nino 3.4 yang Stasioner (Hasil Differencing orde satu dan Differencing orde satu seasonal)
Berdasarkan Gambar 5 dapat ditentukan orde untuk model ARIMA deret input yang selanjutnya dipilih model dengan nilai AIC terkecil dari seluruh kandidat model yang ada. Kandidat model ARIMA deret input dan nilai AIC dapat dilihat pada Tabel 1.
Tabel 1. Kandidat Model ARIMA Deret Input
|
No. |
Model ARIMA |
AIC |
|
1 |
*)ARIMA(1,1,0)(1,1,1)12 |
10,20745 |
|
2 |
ARIMA (0,1,1)(0,1,1)12 |
42,71937 |
|
3 |
ARIMA (0,1,1)(1,W2 |
42,96602 |
|
4 |
ARIMA(1,1,0)(1,1,0)12 |
43,00863 |
|
5 |
*)ARIMA(1,1,0)(0,1,1)12 |
9,21353 |
|
6 |
*)ARIMA(1,1,1)(0,1,1)12 |
10,49803 |
|
7 |
ARIMA (1,1,1)(1,1,0)12 |
40,88339 |
|
8 |
ARIMA(0,1,2)(0,1,1)12 |
34,61827 |
|
9 |
ARIMA(0,1,3)(0,1,1)12 |
25,13985 |
|
10 |
ARIMA (0,1,1)(2,1,0)i2 |
26,1893 |
|
11 |
ARIMA (1,1,0)(2,1,0)i2 |
33,31852 |
*)Estimasi parameter tidak signifikan
Pada Tabel 1 terlihat bahwa model yang semua estimasi parameternya signifikan dengan nilai AIC terkecil adalah ARIMA(0,1,3)(0,1,1)12 yang ditulis sebagai (1 - B)(1 - B1¾ = (1 + Θ1B + Θ2B2 +
Θ3B3)(l + Θ1B1¾
⇔ (1- B - B12 + B13)xt = (1 + Θ1B +
Θ2B2 + Θ3B3)(1 + ΘιB12¼
⇔ Xt - xt-1 - xt-12 - xt-13
= (1 + Θ1B+Θ2B2 + Θ3B3 +
Θ1B12+ Θ1Θ1B13 +
Θ1Θ2B14 + Θ1Θ3B15)εt
⇔ xt = xt-1 + *t-12 + ^t-13 + (1 + θ1b + Θ2B2 + Θ3B3 + Θ1B12 + Θ1Θ1B13 + Θ1Θ2B14 + Θ1Θ3B15)εt (1)
Model ARIMA(0,1,3)(0,1,1)12 pada persamaan (1) menggambarkan bahwa deret input indeks Nino 3.4 pada bulan ini dipengaruhi oleh indeks Nino 3.4 pada satu bulan, dua belas bulan, dan tiga belas bulan sebelumnya.
Prewhitening Deret Input dan Deret Output
Proses prewhitening deret input dilakukan untuk membuat deret input menjadi white noise. Namun, proses prewhitening deret output tidak harus menjadikannya white noise. Proses prewhitening masing-masing deret dilakukan dengan mentransformasi model ARIMA deret input yang diperoleh pada tahap sebelumnya, sehingga deret input setelah di-prewhiening (αt) ditulis pada persamaan berikut.
^t = ^t-1 + ^t-12 + ^t-13 + (1 + θ1b + θ2b2 +
Θ3B3 + θ1B12+ θ1Θ1B13 + θ1Θ2B14 +
Θ1Θ3B15)αt
⇔ Xt = Xt-1 + ^t-12 + *t-13 + αt + θ1at-1 + θ2at-2+ θ3at-3 + θ1αt-12 + θ1θ1αt-13 + θ1θ2αt-14 + θ1θ3αt-15
⇔ αt = %t - %t-1 - *t-12 - *t-13 - θ1αt-1 -θ2at-2- θ3at-3 - θ1αt-12 - θ1θ1αt-13 -θ1θ2αt-14 - θ1θ3αt-15
(2) dengan Θ1 =-0,62782; Θ2 =-0,45179; Θ3 = -0,35351; θ1 = 0,47046; αt adalah deret input yang telah di-prewhitening dan tetapkan
a1,a2,a3,^,a13 = 0, Sehinggapersamaan (2) menjadi
Ut=xt- *t-1 - *t-12 - *t-13 + 0,62782^-1 +
0,45179αt-2 + 0,35351αt-3 -0,47046αt-12 + 0,2954αt-13 + 0,2125αt-14+ 0,1663αt-15. (3)
Dengan melakukan transformasi yang sama seperti prewhitening deret input, sehingga diperoleh
βt = yt -yt-1 -yt-12 -yt-13 + 0,627Wt-1 +
0,45179βt-2 + 0,35351βt-3 -
0,47046βt-12 + 0,2954βt-13 +
0,2125βt-14+ 0,1663βt-15. (4)
Perhitungan Korelasi Silang Deret Input dan Deret Output
Perhitungan korelasi silang bertujuan untuk mengetahui tingkat keeratan hubungan antara variabel αt dan βt. Perhitungan korelasi silang dilakukan untuk menentukan nilai r, s, b dengan mengidentifikasi plot korelasi silang.

Gambar 6. Plot Korelasi Silang
Gambar 6 menunjukkan bahwa lag yang pertama signifikan adalah lag-1. Hal ini menjelaskan bahwa indeks Nino 3.4 memengaruhi curah hujan pada satu bulan sebelumnya.
Penentuan Nilai (b,s,r)
Berdasarkan plot korelasi silang pada Gambar 6 dapat ditentukan nilai (b, s, r) berikut.
-
a. Nilai b = 1 diperoleh dari lag yang pertama signifikan pada plot korelasi silang;
-
b. Nilai s diperoleh dari lag-lag yang signifikan setelah lag -1, sehingga s = 0;
-
c. Nilai r = 0 diperoleh dari pola yang jelas pada plot korelasi silang.
Model fungsi transfer awal dengan (b, s, r) = (1,0,0) yang ditulis sebagai
(m∩ - m1B - ω2B2 - ••• - ωςBs)
yt =------------^T(B)------------λ + ηt
yt = ω∩%t-1 + ηt.
dengan nilai ω∩ = -42,85707, sehingga model fungsi transfer awal yaitu
yt = -42,85707%t-1+ηt. (5)
Identifikasi Model ARIMA Deret Noise
Deret noise dapat dihitung dengan melakukan transformasi model fungsi transfer awal. Berikut persamaan untuk memperoleh nilai-nilai deret noise.
ηt =yt+42,85707%t-1
Tahapan selanjutnya adalah menentukan model deret noise berdasarkan pada plot ACF dan PACF deret noise untuk memperoleh nilai
(pn,0,qn) untuk model ARIMA deret noise. Berdasarkan hasil pendugaan model ARIMA deret noise didapatkan beberapa kandidat model fungsi transfer untuk masing-masing model ARIMA noisenya antara lain :
-
a. ARIMA(1,0,0)
1 yt-ωoχt-ι+(1-^εt.
-
b. ARIMA(0,0,1)
yt - OoXt-I + (1 + θιB)εt.
c.
ARIMA(1,0,1)
, (1+01 B)
yt - ω0x +7—-“S t.
t 0tl (1-φ1B) t
yt - ω0Xt-1 + (1 +Θ1B)εt.
1 yt=ωoχt-1+(1-φB)εt.
1 yt=ωoχt-1+(1-φB-φB25εt.
Estimasi Parameter Model Fungsi Transfer
Tahapan selanjutnya, melakukan estimasi parameter pada semua kandidat model yang telah diduga pada tahap sebelumnya. Hasil estimasi parameter diperoleh yaitu :
|
1 | |
|
a. yt - |
,93 9 xt-1 , (1+o,o8663B)εt. |
|
b. yt- |
-42,91442xt-1 + (1 + 0,06304B)εt |
|
c. yt - |
-43,10764xt.1 +^1-0,54069B)εt. t 1 (1+0,67068B) t |
|
d. yt- |
-45,94224xt-1 + (1 + 0,99982B)εt |
|
e. yt - |
Q7 |
|
, t-1 (1+0,38724B) °t. | |
|
f∙ yt - |
-36,57478xt-1 |
.
.
+----------1---------“Si .
(1+0,56984B+0,50420B2) t
Uji Diagnostik Model
Terdapat dua tahap uji diagnostik model fungsi transfer antara lain
-
1. Perhitungan autokorelasi nilai residual pada model
Perhitungan autokorelasi residual dilakukan untuk menguji kelayakan model. Hasil perhitungan autokorelasi
menunjukkan p — value pada setiap lag lebih besar dari α = 0,05 maka model terbaik yang terpilih tersebut tidak ada korelasi antarsisaan atau white noise.
-
2. Perhitungan korelasi silang
Perhitungan korelasi silang menunjukkan nilai p — value lebih besar dari α = 0,05 pada semua lag. Hal ini berarti nilai residual pada model dengan deret input saling bebas.
Pemilihan Model Terbaik
Model terbaik dipilih berdasarkan nilai AIC terkecil. Model fungsi transfer terbaik yaitu yt = -36,57478xt.1 +--------1--------ε t.
-
t t 1 (1+0,56984B+0,50420B2) t
Nilai AIC model fungsi transfer tersebut adalah 1334,629.
Peramalan Curah Hujan di Bali
Tahap terakhir dari analisis model ARIMAX (model fungsi transfer) yaitu meramalkan curah hujan bulanan di Bali pada tahun 2020. Berikut ini hasil peramalan curah hujan bulanan di Bali pada periode Januari 2020—Desember 2020.
Tabel 2. Hasil Peramalan Curah Hujan pada Januari 2020–Desember 2020
|
Tahun |
Bulan |
Hasil Peramalan (mm) |
Data Aktual (mm) |
|
2020 |
Januari |
195.9347 |
192,2 |
|
Februari |
351.7272 |
371,5 | |
|
Maret |
187.5347 |
216,7 | |
|
April |
54.7954 |
56,3 | |
|
Mei |
84.8899 |
91,4 | |
|
Juni |
133.7899 |
145,1 | |
|
Juli |
15.9087 |
17,7 | |
|
Agustus |
4.1112 |
3,0 | |
|
September |
32.9991 |
38,9 | |
|
Oktober |
177.6589 |
197,0 | |
|
November |
55.6541 |
42,1 | |
|
Desember |
338.9763 |
349,8 |
4. KESIMPULAN DAN SARAN
Sesuai dengan pemaparan pada analisis dan pembahasan dapat diambil kesimpulan bahwa model terbaik untuk meramalkan data curah hujan bulanan di Bali dengan menggunakan model ARIMAX adalah :
yt = -36,57478χt-ι + (1+056984B+050^^
Hasil peramalan curah hujan di Bali dengan menggunakan pemodelan ARIMAX diperoleh nilai mean absolute percentage error (MAPE) sebesar 15,7929% yang menunjukkan hasil peramalan baik.
Saran untuk penelitian yang akan datang untuk melakukan peramalan curah hujan di Bali dengan menggunakan metode peramalan yang lain dan menambahkan variabel eksogen
lainnya yang dapat memengaruhi curah hujan seperti kelembapan udara, temperatur udara, maupun kecepatan angin.
DAFTAR PUSTAKA
Dini, N. S. (2012). Peramalan Kebutuhan Premium dengan MetodeARIMAX untuk Optimasi Persediaan di Wilayah TBBM Madiun. Jurnal Sains dan Seni ITS Vol. 1, No. 1, hal. D-230 s.d D-235.
Harahap, M. R., & Suharsono, A. (2014). Analisis Peramalan Penjualan Sepeda Motor di Kabupaten Ngawi dengan ARIMA dan ARIMAX. Jurnal Sains dan Seni POM ITS Vol. 3, No.2.
Makridakis, Wheelwright, & McGee. (1999). Metode dan Aplikasi Peramalan Edisi kedua. Jakarta: Erlangga.
Wangdi, K., Singhasivanon, P., Silawan, T., Lawpoolsri, S., White, N. J., &
Kaewkungwal, J. (2010). Development of Temporal Modelling for Forecasting and Prediction of Malaria Infections Using Time-Series and ARIMAX Analyses: A Case Study in Endemic District of Bhutan. Malaria Journal.
Wei, W. W. (1994). Univariate and Multivariate Methods. California: Addison Wesley Publishing Company.
191
Discussion and feedback