EBLUP-SMALL AREA ESTIMATION METHOD FOR PER CAPITA EXPENDITURES IN BALI

E-Jurnal Matematika Vol. 11(1), Januari 2022, pp. 58-63

DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p361

ISSN: 2303-1751

EBLUP-SMALL AREA ESTIMATION METHOD FOR PER CAPITA EXPENDITURES IN BALI

Luthfatul Amaliana^1§, Made Laras Setyana Dewi²

¹Jurusan Statistika, Fakultas MIPA – Universitas Brawijaya [Email: [email protected]] ²Jurusan Statistika, Fakultas MIPA – Universitas Brawijaya [Email: [email protected]] ^§Corresponding Author

ABSTRACT

Small Area Estimation (SAE) is a statistical technique for estimating the parameters of a subpopulation with a small sample size. SAE aims to improve the accuracy of parameter estimation, with indirect estimation. This study aims to determine the best method between empirical best linear unbiased prediction (EBLUP) and spatial EBLUP methods (with a queen contiguity weighted matrix) in estimating per capita expenditure per sub-district in Bali. The results of this study indicate that the best SAE method in estimating per capita expenditure per sub-district in Bali is the EBLUP method with the smaller mean squared error. The EBLUP estimation results are significantly influenced by three variables, namely the population, public primary schools, and families using PLN. The sub-district with the highest per capita expenditure in Bali is Denpasar Selatan sub-district. Meanwhile, the sub-district with the lowest per capita expenditure was Abang sub-district. Since the EBLUP model is better than SEBLUP model, this indicates that per capita expenditure per sub-district in Bali is not influenced by its neighbors.

Keywords: Per Capita Expenditures, Bali, EBLUP, SEBLUP, Small Areas Estimation

• 1.    INTRODUCTION

Survei sosial ekonomi nasional (SUSENAS) conducted by Badan Pusat Statistik (BPS) is a survey activity to collect information/data on population, health, education, family planning, housing, consumption, and expenditure. This survey is designed to have three datasets (modules) which held every three years. These modules are the household consumption/expenditure module, the social, cultural and educational module, and the housing and health module (BPS, 2013). The poverty in an area is a representation of the community welfare which can be seen on the expenditure module.

According to BPS (2019), measurement of poverty is carried out using the concept of the ability to meet basic needs. This approach views poverty as an economic inability to meet basic food and non-food needs as measured in terms of expenditure. Therefore, the poor are those who have an average expenditure per capita per month below the poverty line. One of the government's efforts to overcome the

poverty problem is to predict poor areas down to the level of small areas such as districts/cities, sub-districts and villages. The sample system in a population survey in a small area causes a limited number of survey objects. The limitation means the direct estimates cannot produce an accurate estimate. In order to produce better predictions, the indirect estimation method can be used in a small area (Rao, 2003).

Small area estimation (SAE) is an indirect estimation that utilizes information from the surrounding area related to parameters. This method conducted as an effort to suppress a large variety of direct estimates. This method is used as an attempt to suppress a large variety of direct estimates. One of the SAE methods that can be used in estimating small areas is the empirical best linear unbiased prediction (EBLUP) (Sidauruk, et al., 2013). The estimation using the EBLUP method on continuous data needs to be evaluated. This is because the estimator obtained in a small area

is a biased estimator with a minimum variance. The purpose of estimating the EBLUP method is to obtain an efficient estimator. Estimator accuracy can be obtained by measuring the mean square error (MSE). The smaller the MSE, the more accurate an estimator will be.

The indirect estimator of small area is obtained by weighting the random variable of an area to increase the effectiveness of the sample size and minimize the variance. Heterogeneity of an area can be influenced by the surrounding area. This heterogeneity is summarized in spatial effects of the area which can be contained in random effect variable. The EBLUP method that accommodates spatial effects in the model is known as the spatial EBLUP method (SEBLUP) (Pratesi and Salvati, 2008).

Mutualage (2012) conducted a study which show that the SEBLUP method is better than EBLUP for estimating per capita expenditure of villages in Jember District. While Sidauruk, et al. (2013) showed that the characteristics of the parameter β obtained by simulation data on SAE are biased estimators. However, the bias is very small with minimum variance, so that the EBLUP parameter estimates are close to the actual parameters. Another study of Nusrang, et al. (2017) supports Matualage's results which using simulation data showed that the violation of homoscedasticity assumption of random effect of error caused the EBLUP estimator to be in-optimum and biased, so the SEBLUP estimator would give a better prediction than the EBLUP estimator.

This study was conducted to estimate poverty based on per capita expenditure per sub-district in Bali by using the EBLUP and SEBLUP methods (with queen contiguity spatial weighted matrix). Bali is the province with the second lowest poverty rate in Indonesia. This research is expected to provide information about the welfare of the community which is reflected in per capita expenditure per district in Bali. In addition, the EBLUP model that is produced can also provide information on factors that are significant in determining per capita expenditure per sub-district in Bali.

• 2.    RESEARCH METHODS

The data used in this study is secondary data from BPS in 2018. The response variable

used in this study is per capita expenditure per sub-district which comes from Bali dalam Angka 2018. Meanwhile, the predictor variables including the population, public health centers, public primary schools, and families using PLN (Perusahaan Listrik Negara). The unit population in this study in sub-districts in Bali Province. The operational definition of each variable in this study is summarized in Table 1.

Table 1. Operational Definition of Variables
No.    Variables	Variable Definitions
1.    Per capita	Average per capita
expenditure	expenditure per month
(Vi)	(share of monthly household expenditure (Rp) with the number of household members (people)) at the subdistrict level in Bali (in Rupiah)
2.    Population	Total population per subdistrict in Bali (people)
3.    Public health	Number of health centers
centers	per sub-district in Bali
4.    Public	Number of public primary
primary	schools per sub-district in
schools	Bali
5.    Families	Number of families using
using PLN	PLN per sub-district in Bali

The steps of analysis in this study can be described as follows:

• a.    Preparing data as direct estimator. The direct estimator is per capita expenditure per sub-districts in Bali.

• b.    Preparing data as predictor variables. These variables are the population, public health centers, public primary schools, and families using PLN.

• c.    Preparing a spatial weighted matrix (W). This matrix only contains 0 and 1 values. If two sub-districts are side by side and intersect, then it is represented by the value w_ij = 1, while w_ij = 0 otherwise.

• d.    Estimating the parameter of EBLUP and SEBLUP models  (β_i)  by using

generalized least square (GLS) method.

• e.    Estimating the random effects (Vj) of EBLUP and SEBLUP models by using GLS method.

• f.    Estimating per capita expenditure based on the EBLUP and SEBLUP models for each sub-district in Bali.

• g.    Estimating the MSE of EBLUP and SEBLUP for each sub-district in Bali.

DOI: https://doi.org/10.24843/MTK.2022.v11.i01.p361

• h.    Comparing the MSE of EBLUP and SEBLUP models.

• 3.    RESULT AND DISCUSSION

  • 3.1.    Descriptive Analysis

Descriptive analysis is used to determine an overview of Bali data in this study, especially about per capita expenditure. The following descriptive analysis for per capita expenditure is presented in Table 2.

Table 2. Descriptive Statistics

Variable	Min	Max	Average
Per capita expenditure	104,257 (Marga)	6,476,787 (Denpasar Selatan)	1,403,789

Table 2 shows that the lowest per capita expenditure is Rp. 104,257 namely Marga Subdistrict. Meanwhile, the subdistrict with the highest per capita expenditure was Denpasar Selatan Sub-district, which was Rp. 6,476,787.

• 3.2.    EBLUP-SAE Model

The parameters (βj) and the random effects (Vj) of EBLUP model need to be estimated before estimating per capita expenditure per sub-district in Bali. Because of the difference units in each variable, it is necessary to standardize data. According to these estimators of β_i and V_i, the EBLUP model can be written as (1).

⅛ = χjβ^+ Vj   ^

• =    ×ιiβι ^{+ x}2iβ2 ^{+ χ}3iβ3 ^{+ x}4i∕^4 ^{+ V}i

• =    105,148.687 x_1i + 11.548 x_2i +

• 3 7.373 x_3i + 14,733,142 x_4i + V_i       (1)

The estimation results according to EBLUP model in (1) is summarized in Table 3.

Table 3. Per Capita Expenditure (EBLUP Model)

Subdistrict	EBLUP Estimator	Subdistrict	EBLUP Estimator
Abiansemal	2,321,936.84	Tegallalang	998,436.67
Kuta	266,218.10	Ubud	962,849.27
Kuta Selatan	3,118,038.68	Jembrana	341,284.48
Kuta Utara	2,313,222.30	Melaya	741,689.80
Mengwi	3,055,738.75	Mendoyo	831,176.54
Petang	875,073.27	Negara	1,240,263.42
Bangli	1,650,999.04	Pekutatan	583,939.04
Kintamani	2,935,934.20	Abang	221,932.16
Susut	1,339,721.96	Bebandem	724,849.85
Tembuku	975,019.49	Karangase	935,533.37
		m

Subdistrict	EBLUP Estimator	Subdistrict	EBLUP Estimator
Banjar	1,018,800.59	Kubu	756,423.30
Buleleng	4,281,029.59	Manggis	722,404.21
Busungbiu	502,282.07	Rendang	708,230.12
Gerokgak	1,837,704.31	Selat	696,221.52
Kubutambah an	971,817.08	Sidemen	516,300.02
Sawan	1,628,527.15	Banjarangkan	762,227.76
Seririt	1,889,214.28	Dawan	769,065.49
Sukasada	1,371,585.21	Klungkung	1,408,766.29
Tejakula	907,178.57	Nusa Penida	416,153.77
Denpasar Barat	5,337,337.53	Baturiti	598,907.80
Denpasar Selatan	6,006,767.68	Kediri	1,381,440.27
Denpasar Timur	3,037,163.89	Kerambitan	612,911.72
Blahbatuh	1,066,433.44	Marga	262,339.42
Gianyar	1,505,502.85	Penebel	388,734.31
Payangan	917,244.08	Pupuan	929,970.16
Sukawati	3,128,579.90	Selemadeg	429,519.16
Tampaksiring	1,015,423.75	Tabanan	646,380.00

Table 3 shows that the highest per capita expenditure in Bali is Rp. 6,006,747.77, namely South Denpasar Sub-district. Meanwhile, the lowest per capita expenditure is Rp. 221,932,16, namely Abang Sub-district. Testing the error normality assumption is carried out using the Anderson Darling test (α = 5%) with the null hypothesis: e ~ N(0, σf) againts the alternative hypothesis: e ≠N(0,σ²). The result presented in Table 4.

Table 4. Normality Assumption of Error EBLUP Model

Test Statistics	p-value	Decision
0.2407	0.7634	Accept H0

Table 5. Significance of Model EBLUP Parameters
Variable	∙. β	p-value	Decision
Population	0.69813	3.89×10-8	Reject H0
Public health centres Public	0.09688	2.36×10-1	Accept H0
primary schools	-0.26566	1.69×10-2	Reject H0
Families using PLN	0.29973	1.13×10-2	Reject H0

According to Table 4, it can be concluded that the assumption of normality of error is

fulfilled, in other word, the error of EBLUP model spreads normally. Whereas Table 5 summarized the results of testing the significance of the EBLUP model parameters using the t-test (a = 5%). The null hypothesis of this test is: βi = 0 againts the alternative hypothesis: βi ≠ 0.

Table 5 shows that the total population, number of public primary schools, and number of families using PLN variables have a significant effect on per capita expenditure in Bali based on the EBLUP-SAE model.

• 3.3.    Spatial EBLUP-SAE Model

Spatial EBLUP model is a development of EBLUP model that accommodate spatial effect in the model. In the SEBLUP model, a spatial weighting matrix is needed to represent the spatial heterogeneity of each sub-district. The spatial weighting matrix in this study is the queen contiguity matrix as written in (2).

	0	0	0	0	1/8	1/8	0	0	— 0
	0	0	1/3	1/3	0	0	0	0	- 0
	0	1	0	0	0	0	0	0	— 0
	0	1/3	0	0	1/3	0	0	0	- 0
W =	1/5 1/8	0 0	0 0	1/5 0	0 0	0 0	0 0	0 1/8	- 0 - 0	(2)
	0	0	0	0	0	0	0	1/7	-0
	0 ⋮	0	0	0	0	1/9	1/9	0	-0
	0	0	0	0	0	0	0	0	-  0.

The SEBLUP model can be written as in (3).

y = Xβ + Zv + e                  (3)

where v = (I - pW)^-1u. The SEBLUP in (3) can be rewritten as in (4).

y = Xβ + Z((I - PWy¹U) + e     (4)

The estimation of per capita expenditure per district using the SEBLUP method is carried out by first estimating the SEBLUP parameter (β_i), random effect (v) and autoregression coefficient (p) in the model. The estimation of random effect can be obtained by (4), where p = 0.18107 and W is the weighting matrix. Based on the results of the parameter, random effect, and autoregression coefficient of the SEBLUP model, as well as the previous weighting matrix, the SEBLUP model is obtained as written in (5).

yι^s = χιβ + ⅛

= X1iβ1 + X2iβ2 + X3iβ3 + X4iβ4 + Vi

= 105.162,321 X_1i + 11,567 X_2i +

37,432 X_3i + 14.723,051 X_4i + v_i^s (5)

The estimation results of SEBLUP model in (5) is presented in Table 6.

Table 6. Per Capita Expenditure (EBLUP Model)

Sub-district	SEBLUP Estimator	Sub-district	SEBLUP Estimator
Abiansemal	2,353,593.08	Tegallalang	991,349.75
Kuta	274,613.08	Ubud	992,184.90
Kuta Selatan	3,185,553.82	Jembrana	341,042.58
Kuta Utara	2,350,961.26	Melaya	698,124.94
Mengwi	3,071,225.43	Mendoyo	798,673.75
Petang	844,348.70	Negara	1,173,692.51
Bangli	1,631,276.25	Pekutatan	574,391.14
Kintamani	2,951,015.13	Abang	219,787.57
Susut	1,292,811.97	Bebandem	727,355.52
Tembuku	987,930.60	Karangasem	974,942.36
Banjar	1,013,212.11	Kubu	782,559.55
Buleleng	4,278,713.23	Manggis	741,793.61
Busungbiu	501,019.12	Rendang	710,933.05
Gerokgak	1,746,660.94	Selat	710,357.22
Kubutambahan	968,205.47	Sidemen	510,994.89
Sawan	1,610,255.39	Banjarangkan	754,409.17
Seririt	1,898,166.46	Dawan	772,784.20
Sukasada	1,359,359.06	Klungkung	1,423,095.71
Tejakula	894,481.93	Nusa Penida	430,679.82
Denpasar Barat	5,370,533.76	Baturiti	602,569.04
Denpasar Selatan	6,050,927.72	Kediri	1,392,496.16
Denpasar Timur	3,096,984.86	Kerambitan	603,108.84
Blahbatuh	1,071,081.56	Marga	248,671.99
Gianyar	1,504,283.46	Penebel	388,322.74
Payangan	898,585.25	Pupuan	936,196.76
Sukawati	3,083,671.57	Selemadeg	430,699.41
Tampaksiring	977,279.91	Tabanan	622,408.46

Table 6 shows that the highest per capita expenditure in Bali is Rp. 6,050,970.46 and the lowest per capita expenditure is Rp. 219,787,57. Based on the amount of per capita expenditure, the people in the South Denpasar Sub-district are much more prosperous than those in the Abang Sub-district, because of their higher per capita expenditure.

The normality assumption of error in SEBLUP model is carried out using the Anderson Darling test (a = 5%) with the null hypothesis: e~N(0,σ∕) againts the alternative hypothesis: e ^ N(0,σf ). The result is represented in Table 7.

According to Table 7, the assumption of normality of error is fulfilled or the error of SEBLUP model spreads normally. While testing the significance of the SEBLUP model parameters with the null hypothesis: β_i = 0 againts the alternative hypothesis: βι ≠ 0 on the t-test (a = 5%) is summarized in Table 8.

Table 7. Normality Assumption of Error SEBLUP

Model

Test Statistics	p-value		Decision
0.27294	0.6546		Accept H0
Table 8. Significance of Model SEBLUP Parameters
Variable	—■ β	p-value	Decision
Population	0.698396	1.04×10-15	Reject H0
Public health centers	0.100963	1.23×10-1	Accept H0
Public primary schools	-0.26089	6.97×10-4	Reject H0
Families using PLN	0.298222	2.59×10-4	Reject H0

The population, public primary schools, and families using PLN variables in Table 8, have a significant effect on per capita expenditure in Bali based on the SEBLUP-SAE model.

• 3.4.    Comparison of EBLUP and Spatial-EBLUP SAE Models

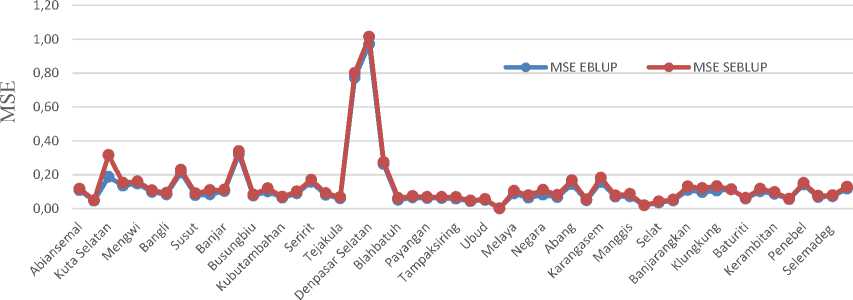
Estimation using the EBLUP and the SEBLUP methods produce the estimated per capita expenditure and MSE of each method. Based on the previous discussion, the estimation result of the EBLUP and SEBLUP methods show the same sub-district in the highest per capita expenditure, namely the South Denpasar Sub-district. It also shows the same sub-district with the lowest per capita expenditure, namely Abang Sub-district. The best model is chosen through the mean square error of both models, where the model with the smallest MSE is best one. The comparison of MSE of both EBLUP and SEBLUP models is presented in Figure 1.

Figure 1 also shows that the MSE of the EBLUP method is smaller than the MSE of the SEBLUP method. In addition, the MSE average of the EBLUP method is lower, which is 0.1233 compared to the SEBLUP method, which is 0.1376. Therefore, the EBLUP-SAE method is better in estimating per capita expenditure in Bali than the SEBLUP-SAE one. Indeed, this condition shows that there is no spatial dependency on per capita expenditure among the subdistricts in Bali Province.

The Comparison of MSE (EBLUP and SEBLUP)

Sub-district

Figure 1. The Comparison of MSE EBLUP and SEBLUP

• 4.    CONCLUSION

Based on the results of this study, per capita expenditure per sub-district in Bali, both the EBLUP and SEBLUP methods, is significant according to population, number of public elementary schools, and number of families using PLN. It is known that the MSE of the EBLUP method is smaller than the MSE of the SEBLUP method with a difference that is not much different. Thus, it can be concluded that the estimated per capita expenditure per district in Bali using the EBLUP method is better than the SEBLUP method. In addition, it can also be said that per capita expenditure per district in Bali has no influence between one sub-district and another.

• 5.    ACKNOWLEDGMENTS

The authors thank to: (1) the Faculty of Mathematics and Natural Science, Brawijaya University; and (2) BPS Bali for providing data.

REFERENCES

BPS. 2013. Survei Sosial Ekonomi Nasional

2013         Kor         Gabungan.

https://microdata.bps.go.id/mikrodata/inde x.php/catalog/220, access on 25 September 2020.

BPS. 2018. Provinsi Bali dalam Angka. Badan Pusat Statistik Provinsi Bali.

BPS. 2019. Kemiskinan dan Ketimpagan. https://www.bps.go.id/subject/23/kemiski nan-dan-ketimpangan.html, accessed on 19 September 2020.

Matualage, D. 2012. Metode Prediksi Tak Bias Linear Terbaik Empiris Spasial pada Area Kecil untuk Pendugaan Pengeluaran per Kapita. IPB Postgraduate School, Bogor.

Nusrang, M., Annas, S., Asfar, A., Hastuty, H., and Jajang, J. 2017. Spatial EBLUP dalam Pendugaan Area Kecil. Sainsmat, 6(1), 59-66.

Pratesi, M., & Salvati, N. 2008. Small area estimation: the EBLUP estimator based on spatially correlated random area effects. Statistical methods and applications, 17(1), 113-141.

Rao, J.N.K. 2003. Small Area Estimation. John Wiley and Sons, US.

Sidauruk, M. A., & Sari, D. K. 2013.

Karakteristik Pendugaan Emperical Best Linear Unbiased Prediction (EBLUP) Pada Pendugaan Area Kecil. Prosiding SEMIRATA 2013, 1(1).

63